1.前言

1. 首先肯定是要學會插入排序再學習希爾排序會更簡單，因為代碼部分有很多相似之處；如果你覺得你很強，可以直接看希爾排序的講解。
2. 哈哈哈！，每天進步一點點，和昨天的自己比

2.插入排序

1. 讓我們先來看看插入排序的動圖，可能第一遍看不懂，最好結合解釋一起看

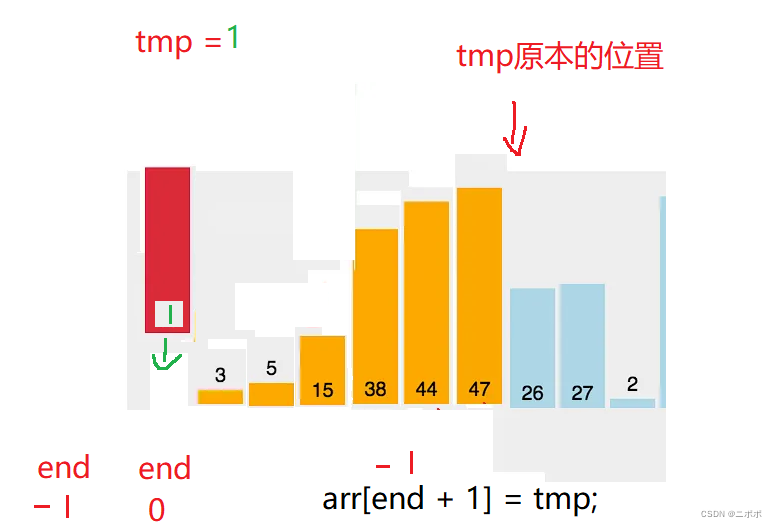
1. 核心思想：end + 1;去0 到 end 之前去找，如果tmp(end+1)小于end位置，end位置往后挪到end + 1位置上
2. 挪動后tmp要繼續找0 到 end的其他位置，如果tmp 比end位置大，就插入在end + 1的位置
3. 需要注意的是：假如tmp大于0到end之間的某一個數據，直接跳出循環，在while循環外面插入
4. for循環的i < n - 1為什么是這樣？ 因為是拿end + 1的位置和前面的比較;
   1. 假設 i < n;那你執行代碼的時候，最后一個是end是n - 1位置，那么你要取tmp位置的就會導致越界，這個tmp就會取到n位置上的數，不就越界了嗎
   2. 0 到 end 之間的區間數據是逐漸增長的，最開始是 0 到 1，第二次范圍就是0 到 2

//插入排序 核心思想：end + 1;去0 end 之前去找，如果tmp小于end位置，就往end位置往后挪
void InsertSort(int* arr, int n)
{//n的位置不可訪問，所以要 < n; < n - 1為什么？ 因為是拿end + 1的位置和前面的比較for (int i = 0; i < n - 1; i++){int end = i;int tmp = arr[end + 1];while (end >= 0)//去查找出0 end范圍的值{if (tmp < arr[end]){arr[end + 1] = arr[end];//如果tmp小于end位置的值，就向后挪，知道大于end位置的值就可以停下插入end--;}else{break;//此時說明tmp大于end位置，在end+1位置插入}}arr[end + 1] = tmp;//防止都比0 end之間要小，小于0跳出循環，-1 + 1；剛好是第一個位置}
}

1. 下面說一種常規思路的寫法，這樣寫可以，不過上面的寫法更好
2. 而且最主要就是防止tmp比 0 到?end 區間內的值都要小

void InsertSort(int* arr, int n)
{//n的位置不可訪問，所以要 < n; < n - 1為什么？ 因為是拿end + 1的位置和前面的比較for (int i = 0; i < n - 1; i++){int end = i;int tmp = arr[end + 1];while (end >= 0)//去查找出0 end范圍的值{if (tmp < arr[end]){arr[end + 1] = arr[end];//如果tmp小于end位置的值，就向后挪，知道大于end位置的值就可以停下插入end--;}else{arr[end + 1] = tmp;break;//此時說明tmp大于end位置，在end+1位置插入}}if(end == -1) {arr[end + 1] = tmp;}

2.1插入排序的時間復雜度

1. 最壞情況：
   1. O(N^2);當排序為逆序時，你想想0 到 end位置的數，假設是升序；竟然是升序但是end + 1這個數據是比0 到 end位置的數還要小那么就會交換很多次
   2. 假如上述的情況每次都這樣呢？，那不是最壞的情況了
   3. 但是逆序的概率很低，反而亂序的概率大些
2. 最好情況：O(N),已經非常接近有序了
3. 還有一點，主要是插入排序適應能力強，在查找的過程中可以直接插入數據，比冒泡排序省去很多查找
4. 這里也順便提一下冒泡排序吧，做個比較

2.2冒泡排序

1. 最壞情況：O(N^2);
2. 最好情況：O(N),已經有序了
3. 雖然冒泡和插入排序時間復雜度都是一樣的，但是在同一所學校，同一個公司；但是它兩之間仍然有好壞之分
4. 為啥呢？ 因為冒泡排序的最壞情況很容易達成，幾乎每次交換都是一個等差數列，最好情況的情況概率太低了
5. 竟然這么菜，有啥用呢 ？ 實踐中沒有意義；適合教學

//冒泡排序
void BubblSort(int* arr, int sz)
{for (int i = 0; i < sz - 1; i++){int flag = 0;//假設這一趟沒有交換已經有序for (int j = 0; j < sz - i - 1; j++){if (arr[j] > arr[j + 1]){int tmp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = tmp;flag = 1;//發生交換，無序}}if(flag == 0)//經過一趟發現有序，沒有交換break;}
}

3.希爾排序

1. 希爾排序分為兩步
   1. 預排序（讓數組接近有序）
   2. 插入排序
2. 插入排序思想不錯，可不可以優化一下，變得更好，甚至更強呢？
3. 插入排序就是怕逆序的情況，所以通過預排序讓數組接近有序，讓大的值跳gap步可以很快的到后面
4. 那么什么是gap，gap就是把數據分為gap組，每個數據間隔為gap的

3.1預排序

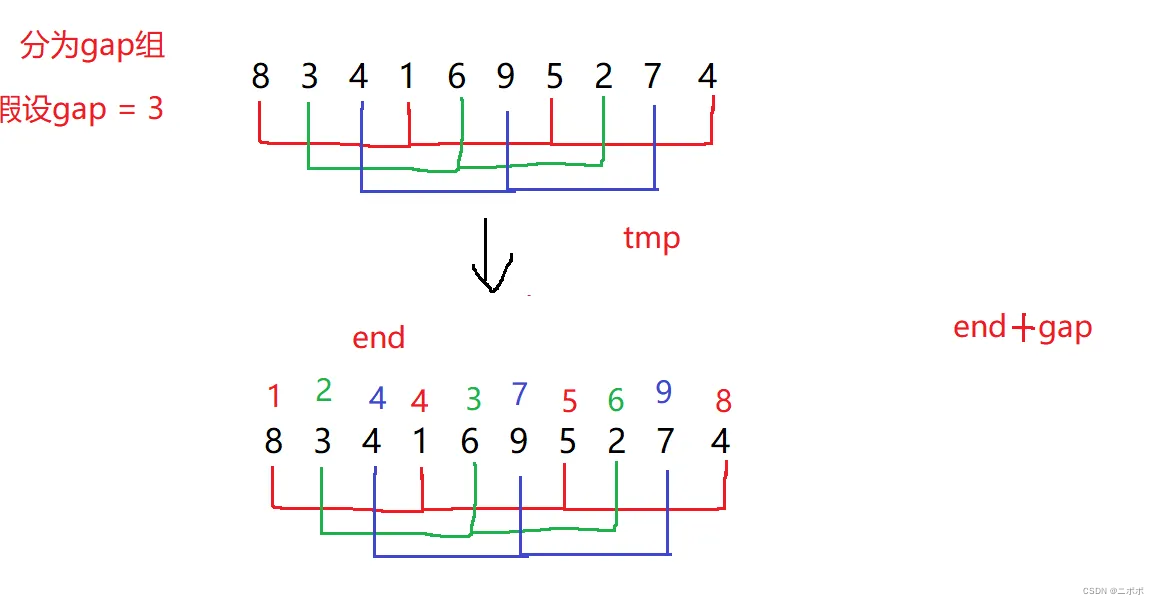
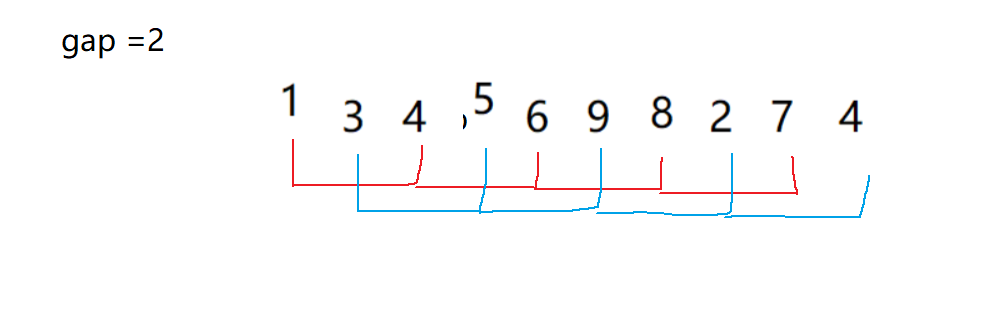
1. 下面這樣圖，看不懂沒關系細細給你分析。可以看到gap = 3，分成了紅綠藍三組數據
2. 每組的每個數間隔為gap，假如說紅色這一組它有4個數，其實你可以看成插入排序的一趟排序，只不過就是間隔為gap而已
3. 而下面這樣圖就是，每組數據都進行一趟插入排序，可以自己畫圖試試看看，一不一樣；當然下面也有動圖的解釋

3.2單趟排序

1. 其實和插入排序思路差不多，只不過是end位置 和 tmp(end + gap)位置進行比較
2. 如果tmp值小于end位置的值,就讓end位置移動到 end + gap位置
3. break跳出證明tmp大于 arr[end],此時tmp就放到end + gap位置即可
4. 放在while循環外，和上面講的插入排序的解決方法一樣，當小于0 到 end時；防止越界
   1. 動圖來解釋一下，這個動圖忘記設置循環了，所以要觀看就重進一下

講完單趟排序，再來說說應該注意的點：

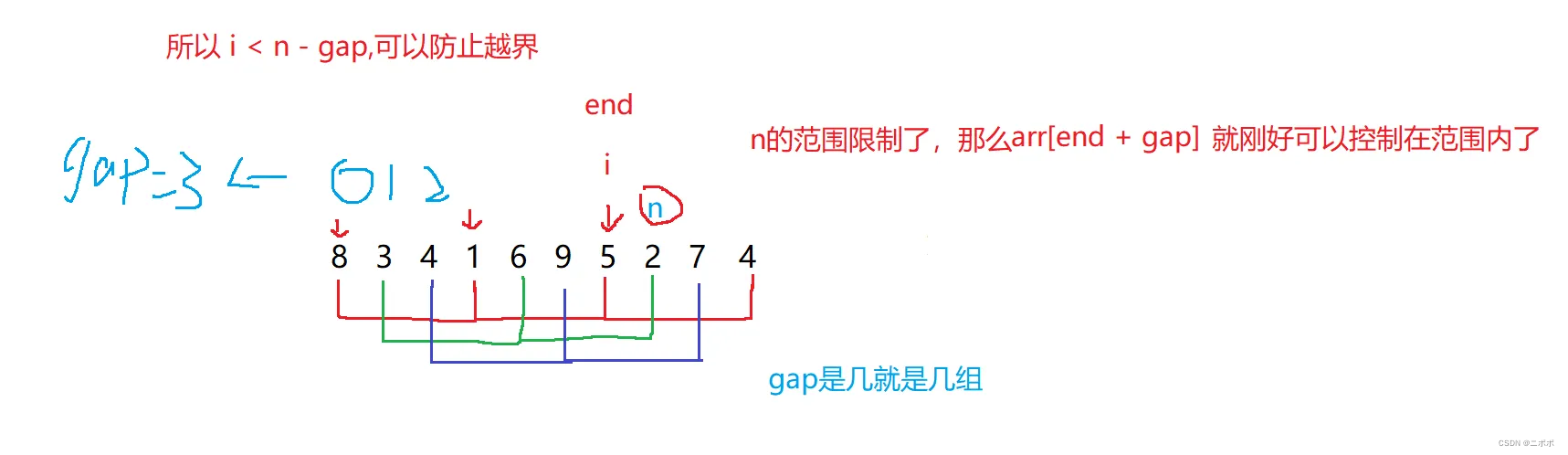
1. 使用for來完成一趟排序的結束條件
2. 紅色這組舉例：因為你每次跳gap步，如果 i 循環到了 數字為4的位置，此時進入循環，int tmp = arr[end + gap];這里面的 + gap會越界

最后是for循環是單趟的代碼

for (int i = j; i < n - gap; i += gap){int end = i;//對應一趟排序的第幾次int tmp = arr[end + gap];while (end >= 0)//比較交換{//如果小于arr[end]挪到arr[end + gap]if (tmp < arr[end]){arr[end + gap] = arr[end];}else{break;}}arr[end + gap] = tmp;}

3.3每組都進行預排序

1. 外面再放一層for循環是什么意思呢？
2. 意思是通過分組來排序，先是紅色然后綠色和藍色，當j = 0是就是紅色這一組

//希爾排序的預排序
void ShellSort(int* arr, int n)
{//假設gap為3int gap = 3;for (int j = 0; j < gap; j++){for (int i = j; i < n - gap; i += gap){int end = i;//對應一趟排序的第幾次int tmp = arr[end + gap];while (end >= 0)//比較交換{//如果小于arr[end]挪到arr[end + gap]if (tmp < arr[end]){arr[end + gap] = arr[end];}else{break;}}arr[end + gap] = tmp;}}
}

1. 當然上面那一種在外面再放一層for也可以
2. 這里我們可以優化一下，變成兩層循環；下面是優化后一小段過程

1. 上面的是一組一組排序，而這里是多組一起排序
2. 而通過整過程發現，紅色會預排序3次，綠色2次，藍色2次；和優化后的總次數一樣 ，假設n = 10，10 - 3 = 7；剛好是7次了
3. 這里并不能通過數循環來判斷時間復雜，上面三層循環和這里的兩次循環一樣的
4. 執行次數一樣，排序的過程不一樣

3.3.1優化后的代碼

void ShellSort(int* arr, int n)
{//假設gap為3int gap = 3;for (int i = 0; i < n - gap; i++){int end = i;//對應一趟排序的第幾次int tmp = arr[end + gap];while (end >= 0)//比較交換{//如果小于arr[end]挪到arr[end + gap]if (tmp < arr[end]){arr[end + gap] = arr[end];end -= gap;}else{break;}}arr[end + gap] = tmp;}
}

3.4預排序要進行多次

1. 這里不是直接預排序完，然后就直接排序；要進行多次預排序才行
2. 那么gap取多少才好呢？，最早有人研究 gap = gap / 2;但是這么最后每組只有兩個，這么分不太好
3. gap = gap / 3 + 1，更加合理一點

1. 這為什么 + 1，因為剛好可以避免被3整除的時候等于了0，帶入值可以想象一下8 / 3 = 2 + 1;3 / 3 = 0 + 1;
2. 也就是說大于3的數除最后都會小于3，+ 1保證最后一個是 1
3. 下面就是進行多次預排序，讓大的數據更快到后面，小的數據更快到前面
4. 弄完預排序，也就完成整個希爾排序，因為gap == 1的時候就是插入排序了

//希爾排序
void ShellSort(int* arr, int n)
{int gap = n;while (gap > 1){//gap > 1 就是預排序//gap == 1 就是插入排序gap = gap / 3 + 1;for (int i = 0; i < n - gap; i++){int end = i;//對應一趟排序的第幾次int tmp = arr[end + gap];while (end >= 0)//比較交換{//如果小于arr[end]挪到arr[end + gap]if (tmp < arr[end]){arr[end + gap] = arr[end];end -= gap;}else{break;}}arr[end + gap] = tmp;}}
}

3.5預排序總結

1. gap越大，大的可以越快的跳到后面，小的可以更快跳到前面，但是就會不接近有序
2. gap越小，跳的越慢，但是更加接近有序，gap == 1相當于插入排序了
3. 所以為了結合兩者優點，直接讓gap慢慢變小

3.6希爾排序的時間復雜度

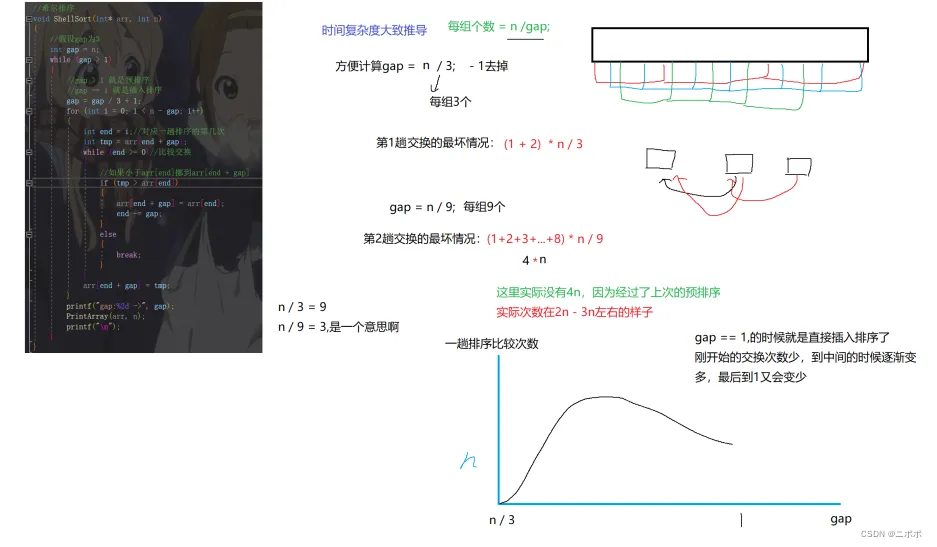
1. 直接給出結論，希爾排序的時間復雜度是O(N^1.3);下面的分析僅供參考！！！
2. 不過下面有稍微推了一下過程，可能不太好
   1. gap大 ：數據量少，交換的次數少；
   2. gap小：數據量大，交換的次數多；
   3. gap表示多少組和數據之間的間隔（gap），gap大，組就多，每組數據就少，gap小 ，組就少，每組數據就多

4.總結

1. 希爾排序的思想非常好，也非常奇妙，估計大部分普通人想不到這個方法；
2. 當然可以學習到這么好的思路，也是很大的進步了；萬一你以后也發明了一種很厲害的算法呢
3. 如果你最近在苦惱要不要寫博客，我的建議是一定寫，個人感覺這個加分項還是很有必要握在手里的