目錄

一、層次分析法（AHP）

二、構造比較判斷矩陣

2.1 兩兩比較法

三、單準則下的排序及一致檢驗

3.1 單準則下的排序

3.2 一致性檢驗

四、層次總排序

4.1 層次總排序的步驟

4.2 總排序一致性檢驗

---

一、層次分析法（AHP）

? ? ? ??方法：層次分析法（Analytic Hierarchy Process）簡稱AHP （美國運籌學家T.L.Saaty教授在70年代中期提出）是指將決策問題的有關元素分解成目標、準則、方案等層次，在此基礎上進行定性分析和定量分析的一種決策方法.

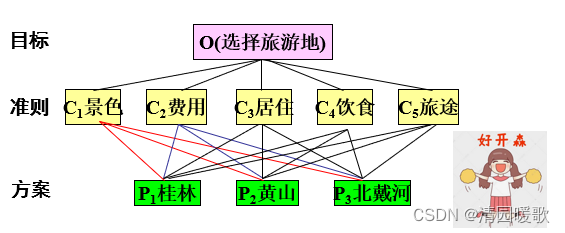
運用層次分析法建模，大體上分成四個步驟:

⑴建立遞階層次結構；

⑵構造比較判別矩陣；

⑶在單準則下的排序及一致性檢驗；

⑷總的排序選優。

二、構造比較判斷矩陣

2.1 兩兩比較法

????????當以上一層次某個因素C作為比較準則時，可用一個比較標度aij來表達下一層次中第i個因素與第j個因素的相對重要性（或偏好優劣）的認識。aij的取值一般取正整數1—9（稱為標度）及其倒數。由aij構成的矩陣稱為比較判斷矩陣A=(aij)。關于aij取值的規則見下表

元素	標度	規?????????? 則
aij	1	以上一層某個因素為準則，本層次因素i與因素j相比， 具有同樣重要。
	3	以上一層某個因素為準則，本層次因素i與因素j相比， i比j稍微重要。
	5	以上一層某個因素為準則,本層次因素i與因素j相比， i比j明顯重要。
	7	以上一層某個因素為準則,本層次因素i與因素j相比， i比j強烈重要。
	9	以上一層某個因素為準則，本層次因素i與因素j相比， i比j極端重要。

aij取值也可以取上述各數的中值2，4，6，8及其倒數，即若因素i與因素j比較得aij，則因素j與因素i比較得1/aij。

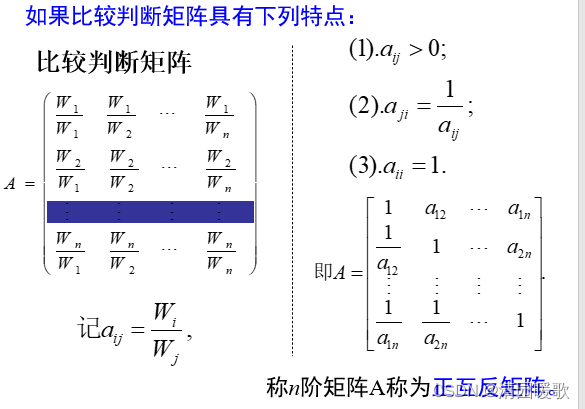
?設n階矩陣A=(aij)為正互反矩陣,? 若對于一切i,j,k,都有aijajk=aik, i,j,k=1,2,…,n,稱A為一致矩陣.

三、單準則下的排序及一致檢驗

3.1 單準則下的排序

????????根據比較判斷矩陣如何求出各因素u1,u2,…,un , 對于準則的相對排序權重的過程稱為單準則下的排序。

（1）理論依據

定理3.1.1 (Perron定理):

設n階方陣A>O, lmax為A的模最大特征根，則

⑴ lmax必為正特征根,且對應特征向量為正向量；

⑵對于A的任何其它特征值，恒有|l|<lmax ；

⑶ lmax為A的單特征根，因而它所對應的特征向量除相差一個常數因子外是唯一的。

定理3.1.2? 對于任何一個正互反矩陣均有lmax 3 n， 其中lmax為A的模最大特征根。

定理3.1.3??? n階正互反矩陣A=(aij)為一致矩陣的充分必要條件是A的最大特征根為n.

（2）求正互反矩陣排序向量的方法

①特征根方法（EVM）

??????? 對于正矩陣，有一種求特征向量的簡易算法（冪法）。下面的定理為冪法提供了理論依據。

②和法

③根法?

3.2 一致性檢驗

?

?引入隨機一致性指標RI

?所以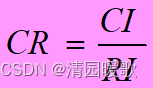

?一般當CR<0.1時，認為A的不一致程度在容許范圍之內，有滿意的一致性，通過一致性檢驗。可用其歸一化特征向量作為權向量，否則要重新構造成對比較矩陣A，對 aij? 加以調整。

四、層次總排序

??????? 計算同一層次中所有元素對于最高層(總目標)的相對重要性標度(又稱排序權重向量)稱為層次總排序。

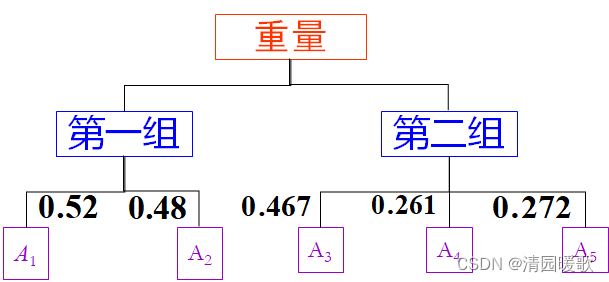
4.1 層次總排序的步驟

4.2 總排序一致性檢驗

????????人們在對各層元素作比較時，盡管每一層中所用的比較尺度基本一致，但各層之間仍可能有所差異，而這種差異將隨著層次總排序的逐漸計算而累加起來，因此需要從模型的總體上來檢驗這種差異尺度的累積是否顯著，檢驗的過程稱為層次總排序的一致性檢驗。