前言：

Dijkstra算法博客講解分為兩篇講解，這兩篇博客對所有有難點的問題都會講解，小白也能很好理解。看完這兩篇博客后保證收獲滿滿。

第一篇博客講解樸素Dijkstra算法Dijkstra求最短路篇一(全網最詳細講解兩種方法，適合小白)(python，其他語言也適用)，本篇博客講解堆優化Dijkstra算法，兩中算法思路大體相同，但時間復雜度有所區別。

• 樸素Dijkstra算法：時間復雜度$O(n^2)$
• 堆優化Dijkstra算法：時間復雜度$O(mlogn)$

兩篇博客給出的題目內容一樣，只有數據規模不一樣。

題目：

題目鏈接：
850. Dijkstra求最短路 II

給定一個 n 個點 m 條邊的有向圖，圖中可能存在重邊和自環，所有邊權均為非負值。請你求出 1 號點到 n 號點的最短距離，如果無法從 1 號點走到 n 號點，則輸出 ?1。

輸入格式
第一行包含整數 n 和 m。
接下來 m 行每行包含三個整數 x,y,z，表示存在一條從點 x 到點 y 的有向邊，邊長為 z。

輸出格式
輸出一個整數，表示 1 號點到 n 號點的最短距離。
如果路徑不存在，則輸出 ?1。

數據范圍（兩題不同處）
$1\le n,m\le 1.5\times 10^5$,
圖中涉及邊長均不小于 0，且不超過 10000。
數據保證：如果最短路存在，則最短路的長度不超過 $10^9$。

輸入樣例：

3 3
1 2 2
2 3 1
1 3 4

輸出樣例：

3

思路：

算法分析：

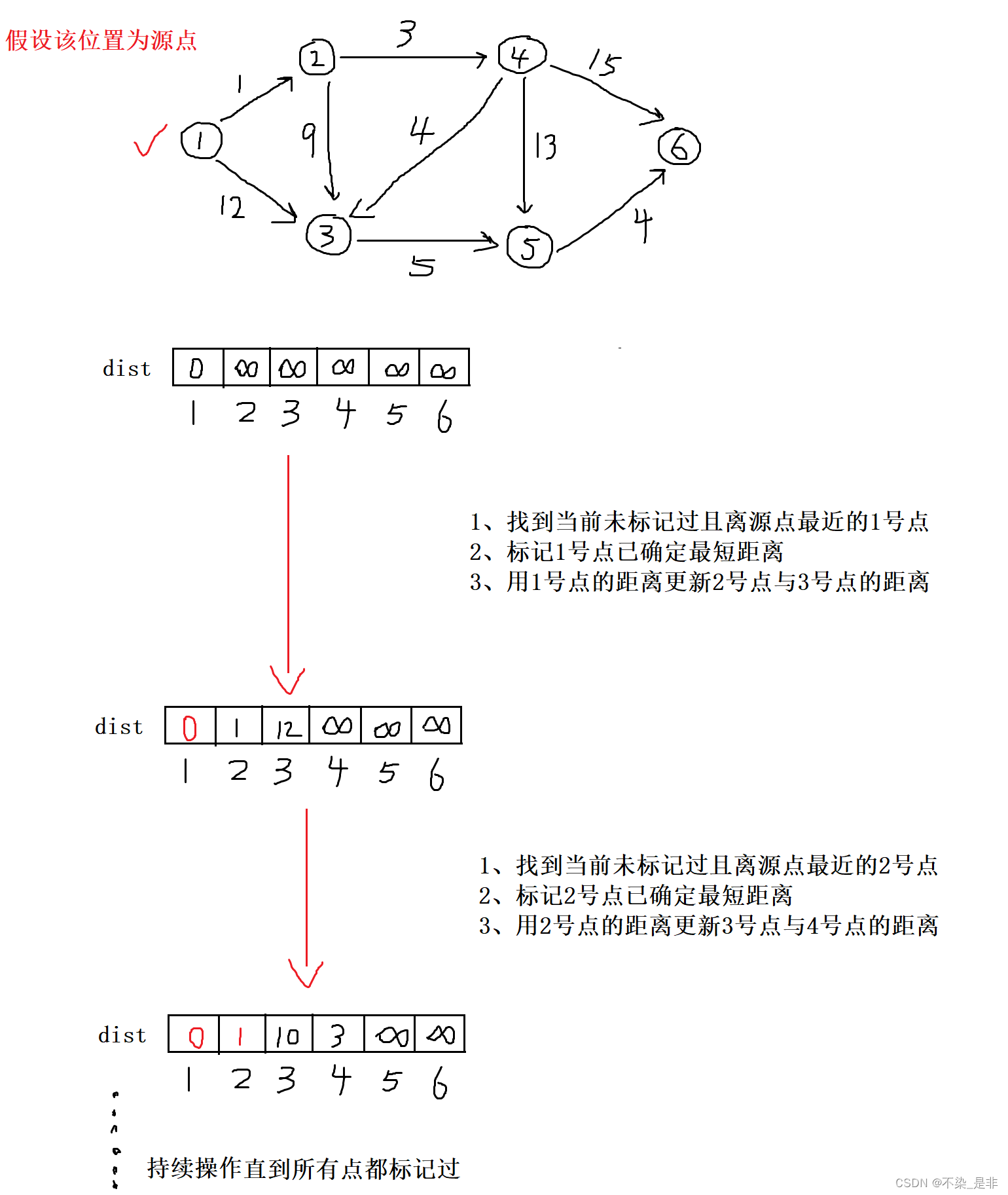
依舊是Dijkstra算法求解，不同的是本題需要降低時間復雜度。

對樸素Dijkstra算法時間復雜度分析可知：

• 尋找路徑最短的點：$O(n^2)$
• 加入集合S：$O(n)$
• 更新距離：$O(m)$
• 所以總的時間復雜度為$O(n^2)$

所以我們需要對尋找路徑最短的點進行改變，如何降低找最短距離的點的時間復雜度呢？
這里可以使用最小堆進行優化（也就是優先隊列），對優先隊列不太熟悉的可以看看優先隊列這篇博客，其他博主寫的很詳細這里我就不介紹了。

進行優化后時間復雜度分析如下：

• 尋找路徑最短的點：$O(n)$
• 加入集合S：$O(n)$
• 更新距離：$O(mlogn)$

堆的數據結構大家接觸的可能有點少，python中有專門的庫函數可以直接使用，其他語言也有類似的庫函數可以使用。

構造鄰接表：

首先對數據進行存儲，圖的存儲有兩種方式，一種是鄰接表，一種是鄰接矩陣。題目中的數據規模用鄰接表存儲（本題數據規模是稀疏圖）。

為什么要用鄰接表去存貯，而不是鄰接矩陣？

我們采用鄰接矩陣還是采用鄰接表來表示圖，需要判斷一個圖是稀疏圖還是稠密圖。稠密圖指的是邊的條數|E|接近于|V|2，稀疏圖是指邊的條數|E|遠小于于|V|2（數量級差很多）。本題是稠密圖，顯然稠密圖用鄰接矩陣存儲比較節省空間，反之用鄰接表存儲。

鄰接表存儲就不需要注意重邊和自環了，因為算法會自動算出最優解

鄰接矩陣存儲代碼如下：

n, m = map(int, input().split())  # 圖的節點個數和邊數
#  構建鄰接表 
num = [[] for i in range(n + 1)]
for _ in range(m):a, b, c = map(int, input().split())num[a].append((b, c))  # 無需考慮重邊和自環

以題目實例為例，打印num數組

[[], [(2, 2), (3, 4)], [(3, 1)], []]

鄰接表構建完成之后就要進行Dijkstra算法，這里直接給出代碼，用詳細代碼給大家進行講解。整體思路跟樸素Dijkstra算法大致相同

代碼及詳細注釋：

import heapqn, m = map(int, input().split())  # 圖的節點個數和邊數
#  構建鄰接表 
num = [[] for i in range(n + 1)]
for _ in range(m):a, b, c = map(int, input().split())num[a].append((b, c))  # 無需考慮重邊和自環
dist = [float("inf") for _ in range(n + 1)]  # float("inf")在python中是無限大的意思
dist[1] = 0  # 源點到源點的距離為置為 0
state = [False for i in range(n + 1)]  # state 用于記錄該點的最短距離是否已經確定def dijstra():# 這里heap中為什么要存兩個值呢，首先小根堆是根據距離來排的，所以有一個變量要是距離，# 其次在從堆中拿出來的時候要知道知道這個點是哪個點，不然怎么更新鄰接點呢？所以第二個變量要存點。heap = [(0, 1)]  # 首先放入距離0和點1，這個順序不能倒，這里顯然要根據距離排序while heap:distance, i = heapq.heappop(heap)  # 這里是取出最下距離和對應的點，最小堆自動取出最小值if state[i]:  # 如果該點最短距離已經確定，跳過下面操作continuestate[i] = True  # 標記該點距離確定for j, d in num[i]:  # 循環遍歷找點i所能到的點和其距離if dist[j] > distance + d:  # 如果原本點j到源點的距離大于后續計算出來的值dist[j] = distance + d  # 更新heapq.heappush(heap, (dist[j], j))  # 該點距離和點加入到最小堆中# 判斷最后一個點的最短距離是否找到，如果為無窮大，則表示未找到，返回-1，否則返回最短距離dist[-1]if dist[n] == float("inf"):return -1else:return dist[n]print(dijstra())

樸素Dijkstra算法大家理解好了本算法也很好理解，操作都是一樣，只是在尋找路徑最短的點時用了最小堆操作。這里就不拿實例帶大家過了，如果略微有點懵，大家可以自己拿實例數據過一遍。

本題主要對 Python 中的 heapq 庫進行簡略講解。

import heapqheap = []
heapq.heappush(heap, (1, 2))
heapq.heappush(heap, (1, 3))
heapq.heappush(heap, (2, 1))
heapq.heappush(heap, (2, 0))
heapq.heappush(heap, (0, 2))
heapq.heappush(heap, (0, 0))print("初始狀態", heap)
print("刪除的元素", heapq.heappop(heap))
print("刪除后狀態", heap)

運行結果：

初始狀態 [(0, 0), (1, 2), (0, 2), (2, 0), (1, 3), (2, 1)]
刪除的元素 (0, 0)
刪除后狀態 [(0, 2), (1, 2), (2, 1), (2, 0), (1, 3)]

• heapq.heappush（(heap, (1, 2)）：把元素（1，2）加入到堆 heap中（每次加入后都是最小堆的構建形式）。
• heapq.heappop(heap)：彈出堆頂元素（最小堆的堆頂就是最小元素）。

總結：

堆優化版dijkstra適合稀疏圖

思路：

堆優化版的dijkstra是對樸素版dijkstra進行了優化，在樸素版dijkstra中時間復雜度最高的尋找距離
最短的點O(n^2)可以使用最小堆優化。

1. 一號點的距離初始化為零，其他點初始化成無窮大。
2. 將一號點放入堆中。
3. 不斷循環，直到堆空。每一次循環中執行的操作為：
   彈出堆頂（與樸素版diijkstra找到S外距離最短的點相同，并標記該點的最短路徑已經確定）。
   用該點更新臨界點的距離，若更新成功就加入到堆中。

時間復雜度分析

• 尋找路徑最短的點：$O(n)$
• 加入集合S：$O(n)$
• 更新距離：$O(mlogn)$