修剪二叉搜索樹

給你二叉搜索樹的根節點?root?，同時給定最小邊界low?和最大邊界?high。通過修剪二叉搜索樹，使得所有節點的值在[low, high]中。修剪樹?不應該?改變保留在樹中的元素的相對結構 (即，如果沒有被移除，原有的父代子代關系都應當保留)。 可以證明，存在?唯一的答案?。

所以結果應當返回修剪好的二叉搜索樹的新的根節點。注意，根節點可能會根據給定的邊界發生改變。

示例 1：

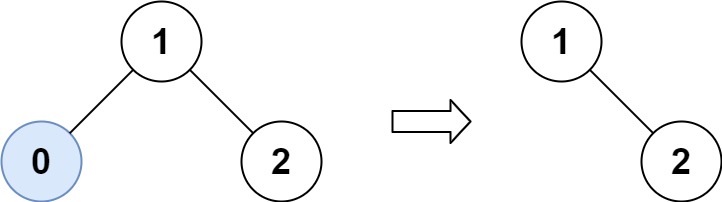
輸入：root = [1,0,2], low = 1, high = 2
輸出：[1,null,2]

示例 2：

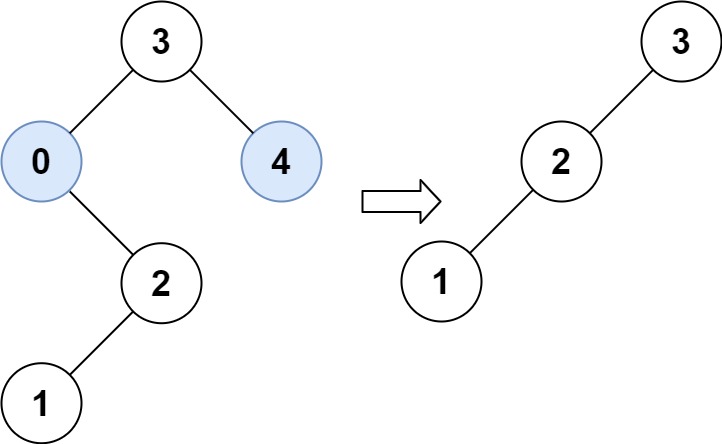
輸入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3
輸出：[3,2,null,1]

提示：

• 樹中節點數在范圍?[1, 104]?內
• 0 <= Node.val <= 104
• 樹中每個節點的值都是?唯一?的
• 題目數據保證輸入是一棵有效的二叉搜索樹
• 0 <= low <= high <= 104

我們在剪枝的時候，要考慮這個節點數字的大小，如果值小于low的話，那我們就先遞歸，再return他的右孩子?；如果大于high的話，就先遞歸，再返回他的左孩子（先遞歸是因為左/右孩子中不一定完全都是在范圍的值）

然后締造聯系即可。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* traversal(TreeNode* cur, int low, int high){if(cur==nullptr)return nullptr;if(cur->val<low){TreeNode* right = traversal(cur->right,low,high);return right;}if(cur->val>high){TreeNode* left = traversal(cur->left,low,high);return left;}cur->left = traversal(cur->left,low,high);cur->right = traversal(cur->right,low,high);return cur;}TreeNode* trimBST(TreeNode* root, int low, int high) {return traversal(root,low,high);}
};

---

將有序數組轉換為二叉搜索樹

給你一個整數數組?nums?，其中元素已經按?升序?排列，請你將其轉換為一棵?平衡?二叉搜索樹。

示例 1：

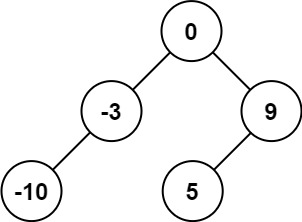
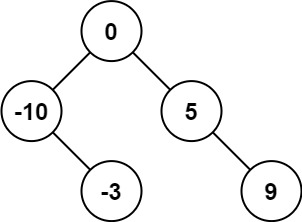
輸入：nums = [-10,-3,0,5,9]
輸出：[0,-3,9,-10,null,5]
解釋：[0,-10,5,null,-3,null,9] 也將被視為正確答案：

示例 2：

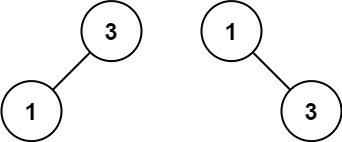
輸入：nums = [1,3]
輸出：[3,1]
解釋：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索樹。

提示：

• 1 <= nums.length <= 104
• -104 <= nums[i] <= 104
• nums?按?嚴格遞增?順序排列

這個題就是每次找到區間的中間值放到節點上，不斷進行劃分。

注意：

1.在找中間值時，要用 left+(right-left)/2這種方式，就不會出現溢出的情況。

2.

 cur->left = traversal(nums,0,temp-1);cur->right = traversal(nums,temp+1,nums.size()-1);

?我寫的時候寫成了這樣，這只能保證二叉樹最左側節點和最右側節點是正常的，而中間的節點就會出問題。

正確代碼如下：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* traversal(vector<int>& nums,int left,int right){if(left>right) return nullptr;int  temp = left + ((right - left) / 2);TreeNode* cur = new TreeNode(nums[temp]);cur->left = traversal(nums,left,temp-1);cur->right = traversal(nums,temp+1,right);return cur;}TreeNode* sortedArrayToBST(vector<int>& nums) {return traversal(nums,0,nums.size()-1);}
};

?

---

把二叉搜索樹轉換為累加樹

給出二叉?搜索?樹的根節點，該樹的節點值各不相同，請你將其轉換為累加樹（Greater Sum Tree），使每個節點?node?的新值等于原樹中大于或等于?node.val?的值之和。

提醒一下，二叉搜索樹滿足下列約束條件：

• 節點的左子樹僅包含鍵?小于?節點鍵的節點。
• 節點的右子樹僅包含鍵?大于?節點鍵的節點。
• 左右子樹也必須是二叉搜索樹。

注意：本題和 1038:?1038. 從二叉搜索樹到更大和樹 - 力扣（LeetCode）?相同

示例 1：

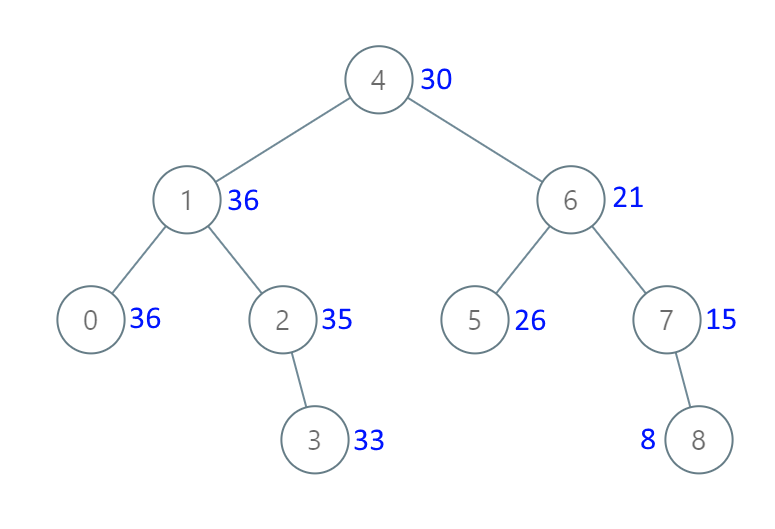
輸入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
輸出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

輸入：root = [0,null,1]
輸出：[1,null,1]

示例 3：

輸入：root = [1,0,2]
輸出：[3,3,2]

示例 4：

輸入：root = [3,2,4,1]
輸出：[7,9,4,10]

提示：

• 樹中的節點數介于?0?和?104?之間。
• 每個節點的值介于?-104?和?104?之間。
• 樹中的所有值?互不相同?。
• 給定的樹為二叉搜索樹。

這道題注意：因為只需要修改每個位置的值，所以遞歸是void類型的。

累加數：其實這就是一棵樹，大家可能看起來有點別扭，換一個角度來看，這就是一個有序數組[2, 5, 13]，求從后到前的累加數組，也就是[20, 18, 13]，是不是感覺這就簡單了。?

也就是我們需要用右中左的順序即可完成。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int pre = 0;void traversal(TreeNode* cur){if(cur==nullptr)return ;traversal(cur->right);cur->val += pre;pre = cur->val;traversal(cur->left);}TreeNode* convertBST(TreeNode* root) {pre = 0;traversal(root);return root;}
};