數據結構-堆(帶圖)詳解

前言

本篇博客我們來仔細說一下二叉樹順序存儲的堆的結構，我們來看看堆到底如何實現，以及所謂的堆排序到底是什么

💓 個人主頁：普通young man-CSDN博客

? 文章專欄：數據結構_普通young man的博客-CSDN博客

? ? ? 若有問題 評論區見📝

🎉歡迎大家點贊👍收藏?文章

目錄

樹的概念

二叉樹的概念及結構

二叉樹的基本定義：

二叉樹的性質：

特殊的二叉樹類型：

存儲結構：

操作與遍歷：

堆

堆的實現

堆實現的接口

Heap_Init-初始化

IF_Add_capacity-擴容

Swap-數據交換

Heap_Push-插入

Upward-向上調整

?編輯

Heap_Pop-刪除

Downward-向下調整

?編輯

Heap_Empty-判空

Heap_Top-獲取堆頂數據

Heap_Destory-銷毀

堆排序

函數部分

Heap_qsort

top-k問題

Top-K問題的基本概念

解決Top-K問題的常見方法

應用實例

問題

樹的概念

在學習堆這個數據結構的時候我們先來了解一下什么是樹？

樹是一種重要的非線性數據結構，它模擬了自然界中樹木的結構，不過在計算機科學中，樹是倒置的，即根在上，葉在下。樹主要由節點（或稱為結點）和邊組成，用于表示具有層次關系的數據集合。

注意：樹的結構子樹之間沒有交際，否則就不成立

  1. 定義：

    • 樹是由一個或多個節點組成的有限集合。如果樹為空，稱為空樹；如果不為空，則滿足以下條件：
      • 有且僅有一個稱為根（root）的節點，它沒有前驅節點（即父節點）。
      • 除根節點外，其余每個節點有且僅有一個父節點。
      • 節點的子節點之間沒有順序關系，但每個子節點都可視為一個子樹。
      • 樹中的節點數可以是任意有限個，包括0（空樹）。

  2. 節點的度：

    • 一個節點的度是指它擁有子節點的數量。葉子節點（或終端節點）是度為0的節點，即沒有子節點的節點。

  3. 樹的度：

    • 樹的度是樹中所有節點的度中的最大值。

  4. 層次與高度：

    • 節點的層次是從根節點到該節點路徑上的邊數。根節點的層次為1。
    • 樹的高度（或深度）是樹中所有節點的層次中的最大值，也就是從根到最遠葉子節點的邊數。

  5. 祖先與后代：

    • 對于非根節點，從該節點到根節點路徑上的所有節點（包括根節點）都是該節點的祖先。
    • 一個節點的后代包括它所有的子節點、子節點的子節點等，直至葉子節點。

  6. 兄弟節點：

    • 具有相同父節點的節點互為兄弟。

  7. 子樹：

    • 任何節點及其所有后代節點構成的樹稱為該節點的子樹。

二叉樹的概念及結構

接下來我們介紹樹中的一種結構二叉樹

二叉樹是一種特殊的樹形數據結構，其中每個節點最多只有兩個子節點，通常被稱作左子節點和右子節點。這種結構使得二叉樹成為計算機科學中研究和應用非常廣泛的數據結構之一。下面是關于二叉樹的一些核心概念和結構特征：

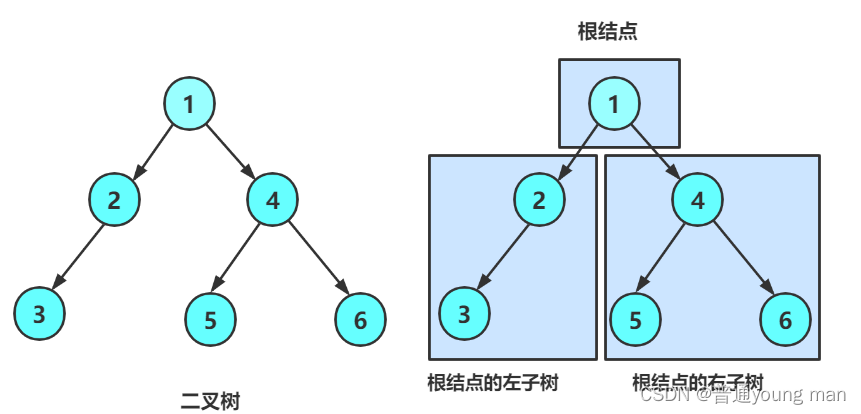
二叉樹的基本定義：

  1. 節點：二叉樹的基本組成單位，每個節點可以包含一個數據元素以及指向其左右子節點的引用。
  2. 根節點：樹的頂端節點，沒有父節點。
  3. 葉子節點：沒有子節點的節點。
  4. 度：節點的子節點數量，二叉樹中節點的度不超過2。
  5. 父子關系與兄弟關系：與一般樹相同，每個節點（除了根）有唯一的父節點，同一父節點的子節點互為兄弟。

二叉樹的性質：

  • 有序性：二叉樹的子節點分為左子樹和右子樹，這給樹帶來了順序，區別于無序的多叉樹。
  • 遞歸定義：一個空集構成空二叉樹，或者由一個根節點加上左右兩個互不相交的二叉樹（左子樹和右子樹）組成。

特殊的二叉樹類型：

  • 滿二叉樹：所有非葉子節點都有兩個子節點，且所有葉子節點都在同一層。
  • 完全二叉樹：除了最后一層，每一層都是滿的，且最后一層的葉子節點都盡可能靠左排列。
  • 二叉排序樹（BST）：左子樹所有節點的值小于根節點的值，右子樹所有節點的值大于根節點的值，且左右子樹也分別是二叉排序樹。

存儲結構：

  • 順序存儲：對于完全二叉樹，可以使用數組來緊湊存儲，利用數組索引來體現節點間的父子關系。
  • 鏈式存儲：更通用的方法，每個節點包含數據和指向左右子節點的指針，通常使用結構體或類來定義節點結構。

操作與遍歷：

  • 遍歷：訪問二叉樹中所有節點的過程，有前序遍歷、中序遍歷、后序遍歷和層序遍歷等方法。
  • 插入與刪除：在二叉排序樹中，根據節點值的比較進行插入或刪除操作，并保持二叉排序樹的性質。

二叉樹因其結構簡單、操作方便，常被用于實現各種高效算法，如查找、排序、圖的遍歷等。在實際應用中，通過選擇特定類型的二叉樹（如AVL樹、紅黑樹），可以達到平衡性和高效的查詢性能。

現實中的二叉樹

現在我們了解二叉樹的一個概念，我們接下來進入正題

堆

其實堆我們的堆就是二叉樹當中的完全二叉樹，現實中我們通常把堆(一種二叉樹)使用順序結構的數組來存儲，需要注意的是這里的堆和操作系統虛擬進程地址空間中的堆是兩回事，一個是數據結構，一個是操作系統中管理內存的一塊區域分段。

堆我們分兩種：大堆 和 小堆

大堆：

在大堆中，每個節點的值都大于或等于其子節點的值。換句話說，父節點總是大于（或等于）其孩子節點。堆頂元素（根節點）因此是整個堆中的最大值。

小堆：

與大堆相反，小堆中的每個節點的值都小于或等于其子節點的值。這意味著父節點總是小于（或等于）其孩子節點，堆頂元素（根節點）是整個堆中的最小值。

請看這張圖

大家知道我們的數據在內存中是b存儲結構的模式(物理存儲)，但是二叉樹是a的邏輯結構，我們的計算機會通過一種叫映射的方式，將這種邏輯結構映射到物理存儲。

可能大家會有疑問為什么不直接用數組，而要用堆這個結構？

數組是一種基礎且靈活的數據結構，適合存儲和訪問連續的數據塊，特別是在索引訪問和隨機訪問方面表現優秀。然而，在某些特定場景下，尤其是涉及到動態調整數據順序、維護數據的某種特定排序狀態或高效地獲取最大值/最小值時，數組的效率可能不如專門設計的數據結構，比如堆。

堆是一種特殊類型的完全二叉樹，它具有以下特點，使其在某些應用場景下比簡單的數組更加高效和適用：

  1. 維護有序性：

    • 最大堆：每個節點的值都大于或等于其子節點的值，堆頂元素始終是最大值。
    • 最小堆：每個節點的值都小于或等于其子節點的值，堆頂元素始終是最小值。 這種特性使得堆在需要頻繁查找最大或最小元素的場景（如優先隊列）中極為高效，無需遍歷整個數組即可快速獲得。

  2. 動態調整：

    • 堆支持插入和刪除元素的同時能夠高效地（通常是O(log n)時間復雜度）重新調整結構以維持其特性，這一點在使用數組時難以直接高效實現。

  3. 內存利用率：

    • 實際實現時，堆可以采用數組來存儲，雖然邏輯上是樹狀結構，但實際上占用的是連續內存空間，因此內存使用相對高效。

  4. 排序應用：

    • 堆可以作為實現堆排序的基礎，這是一種不穩定的排序算法，其優勢在于能夠提供較好的最壞情況和平均時間復雜度（O(n log n)），并且不需要像快速排序那樣依賴于數據的初始分布。

堆的實現

先看一下堆的結構咋寫，其實和順序表的結構一樣，因為堆本身就是數組，只是邏輯看起不是。

//堆的結構
typedef int HeapTypeData;
typedef struct heap
{HeapTypeData* a;int top;int capacity;
}heap;

記住這張圖

堆實現的接口

//初始化
void Heap_Init(heap* obj);
//插入
void Heap_Push(heap* obj, HeapTypeData x);
//刪除
void Heap_Pop(heap* obj); 
//判空
bool Heap_Empty(heap* obj);
//獲取堆頂
HeapTypeData Heap_Top(heap* obj);
//銷毀
void Heap_Destory(heap* obj);
//擴容
void IF_Add_capacity(heap* obj);
//向上調整
void Downward(HeapTypeData* p, int n, int parent);
//向下調整
void Upward(HeapTypeData* p, int child);
//交換
void Swap(HeapTypeData* p1, HeapTypeData* p2);

這些接口是如何實現的嘞？，如何才能創建這么一棵樹？

這些接口我會講解一些沒見過德接口，因為這個堆的接口和順序表差不多

Heap_Init-初始化

//初始化
void Heap_Init(heap* obj) {obj->a = NULL;obj->top = obj->capacity = 0;
}

初始化和順序表差不多，將指針置NULL，其他的值初始化為0

IF_Add_capacity-擴容

//擴容
void IF_Add_capacity(heap* obj) {if (obj->top == obj->capacity){int new_capeccity = obj->capacity == 0 ? 4 : obj->capacity * 2;HeapTypeData* tmp = (HeapTypeData*)realloc(obj->a,sizeof(HeapTypeData) * new_capeccity);if (tmp == NULL){assert("realloc");}obj->a = tmp;obj->capacity = new_capeccity;}
}

Swap-數據交換

//交換
void Swap(HeapTypeData* p1, HeapTypeData* p2)
{HeapTypeData tmp = *p1;*p1 = *p2;*p2 = tmp;
}

Heap_Push-插入

//插入
void Heap_Push(heap* obj, HeapTypeData x) {assert(obj);IF_Add_capacity(obj);obj->a[obj->top] = x;obj->top++;//這個時候我們需要向上Upward(obj->a,obj->top-1);
}

Upward-向上調整

//向上調整
void Upward(HeapTypeData*p, int child){//通過計算找父母HeapTypeData parent = (child - 1) / 2;while (child > 0){if (p[child] < p[parent]){//交換Swap(&p[child], &p[parent]);//交換后，將parent的位置給給child，繼續計算下一個parentchild = parent;parent = (child - 1) / 2;}else{break;}}
}
  • eapTypeData *p: 指向堆數組的指針，這個數組存儲了堆的所有元素。
  • int child: 插入新元素的位置（索引），從0開始計數。新插入的元素被認為是一個“孩子”節點，該函數會檢查并調整這個孩子節點與其父節點的關系，以確保堆的性質不變。

函數執行流程：

  1. 計算父節點位置：首先根據孩子節點的索引child計算出其父節點的索引parent，公式為(child - 1) / 2。
  2. 循環比較并交換：進入一個循環，在循環中不斷比較當前孩子節點和其父節點的值。如果孩子節點的值小于父節點的值（對于最小堆而言），則交換這兩個節點的值。這是因為最小堆要求父節點的值不大于子節點的值。
  3. 更新索引并繼續：在交換之后，原來的子節點變成了新的父節點，因此需要更新child為parent，同時基于新的child計算新的parent，繼續進行比較和可能的交換，直到孩子節點不再小于其父節點或者到達了堆的根部（即child <= 0時）。
  4. 退出循環：一旦發現孩子節點不小于其父節點，或者已經沒有父節點可比較（即到達了樹的根），循環結束，此時堆的性質已經得到恢復。

Heap_Pop-刪除

//刪除
void Heap_Pop(heap* obj) {assert(obj);assert(obj->a);assert(obj->top > 0);//先交換，如果直接刪除堆頂的數據，就會導致血脈混亂Swap(&obj->a[0], &obj->a[obj->top - 1]);//最后--top就刪掉最后一個數據obj->top--;//這邊要考慮一個問題，我們是小堆，但是我們的最大的數在堆頂，所以這里需要將最大的數向下移動，讓次小的數往上補Downward(obj->a,obj->top,0);
}

Downward-向下調整

//向下調整
void Downward(HeapTypeData* p,int n, int parent) {//計算出左兒子int child = parent * 2 + 1;while (child < n){if(child + 1 < n && p[child+1] < p[child]) {//如果右兒子小于左兒子，直接++到右兒子的位置++child;}if ( p[child] < p[parent])//如果child<parent，就交換,要把小的往上走{//這邊操作一樣，算法不同Swap(&p[child],&p[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}
  • HeapTypeData *p: 指向堆數組的指針。
  • int n: 堆中有效元素的數量。在調整過程中，只考慮堆的前n個元素。
  • int parent: 當前需要調整的父節點在數組中的索引位置。

函數執行流程：

  1. 初始化子節點位置：首先計算出當前父節點的左孩子的索引child，公式為parent * 2 + 1。
  2. 循環比較并交換：進入循環，只要child的值小于n，表示還有子節點可以比較。
    • 選擇較小的子節點：如果右孩子存在（即child + 1 < n）且右孩子的值小于左孩子的值，則將child更新為右孩子的索引，因為我們要找到兩個子節點中更小的那個。
    • 比較并交換：如果找到的子節點child的值小于其父節點parent的值，說明違反了最小堆的性質，這時需要交換它們的值，并將當前的child位置作為新的父節點位置繼續向下比較。
    • 更新位置：交換后，原child位置已成為新的父節點位置，因此更新parent = child，并基于新的父節點重新計算其左孩子的索引child = parent * 2 + 1，繼續循環。
    • 退出條件：如果子節點不小于父節點，或者已經沒有更多的子節點可比較（即child >= n），則跳出循環。
  3. 結束：循環結束后，堆的性質得到了恢復，即以parent為根的子樹滿足最小堆的定義。

Heap_Empty-判空

//判空
bool Heap_Empty(heap* obj) {assert(obj);return !obj->top;
}

Heap_Top-獲取堆頂數據

//返回堆頂
HeapTypeData Heap_Top(heap* obj) {assert(obj);assert(obj->a);return obj->a[0];
}

Heap_Destory-銷毀

//銷毀
void Heap_Destory(heap* obj) {if (obj->a){free(obj->a);obj->a = NULL;obj->capacity = obj->top = 0;}
}

堆排序

//堆排序
void Heap_qsort(int *p,int sz) {建堆//for (int i = 1; i < sz; i++)//	Upward(p,i);//}//建堆for (int i = (sz-1-1)/2; i >= 0; i--)//找最后一個不是葉子的節點{Downward(p,sz,i);}//對堆排序int end = sz - 1;while (end > 0){Swap(&p[0],&p[end]);Downward(p,end,0);--end;}
}
int main() {int a[] = {5,8,9,2,1};int sz = sizeof(a) / sizeof(a[0]);//text1();Heap_qsort(a,sz);int n = 3;for (int i = 0; i < n; i++){printf("%d ", a[i]);}return 0;
}

函數部分

Heap_qsort

  • 輸入參數:

    • int *p: 指向待排序數組的指針。
    • int sz: 數組的大小，即元素數量。

  • 過程:

    1. 建堆:
      • 與傳統從第一個非葉節點開始構造堆的方法不同，這里采用了從最后一個非葉節點開始逆序遍歷至根節點的方式來構建最小堆。這樣做的目的是直接通過Downward函數遞歸調整每個子樹為最小堆，最終整個數組構成一個最小堆。計算最后一個非葉節點的索引公式為(sz-1-1)/2，然后從這個索引開始，逐步向前執行Downward操作。
      • (sz-1-1)/2：sz-1->最后一個元素，sz-1-1找到父節點
    2. 堆排序:
      • 首先，將堆頂元素（數組中的最小值）與數組末尾元素交換，確保當前最小值位于正確的位置（即數組末尾）。
      • 然后，因為堆頂元素（現在是數組的末尾元素）已經正確排序，所以縮小堆的有效大小（end -= 1），并在剩下的元素中再次調用Downward函數調整剩余元素為最小堆。這個過程重復，直到整個數組都被正確排序。

  • 輸出:

    • 數組p的內容將會按照升序排列。

這邊我用gif來展示堆排序的邏輯

這邊我建的是一個小堆

排序

那這個堆排序的時間復雜度是多少嘞？

那我們就來算一算

得出結論是n*logn

這里面得計算也可以套公式

top-k問題

Top-K問題是一類在大數據集或流式數據中尋找或維護最頂尖（最大或最小）K個元素的問題。這類問題廣泛應用于各種場景，特別是在需要高效地處理大量數據并提取關鍵信息時，比如數據分析、推薦系統、搜索引擎排名、社交網絡分析、金融風控、大數據處理等領域。

Top-K問題的基本概念

在最簡單的形式中，Top-K問題可以表述為：給定一個包含N個元素的無序集合，找出其中最大的K個元素或最小的K個元素。這里的“最大”或“最小”可以根據具體應用需求定義，比如數值大小、頻率、相關性等。

解決Top-K問題的常見方法

  1. 快速選擇算法：基于快速排序的選擇算法變體，通過一次劃分過程確定一個基準元素的位置，如果基準元素恰好處于第K個位置，則找到答案；否則，在基準元素的正確一側遞歸繼續查找。

  2. 堆方法：維護一個大小為K的小頂堆（找最大K個元素）或大頂堆（找最小K個元素），遍歷數據時，比較堆頂元素與當前元素，如果滿足條件則替換堆頂元素并調整堆結構，保證堆的性質。這種方法的時間復雜度接近O(N log K)。

  3. 二分查找法：適用于能夠計算數組中某個值排名或能夠估算某個值排名的場景。通過二分查找確定一個閾值，然后統計小于或大于該閾值的元素個數，逐步逼近目標K值。

  4. 桶排序或計數排序：對于數據范圍有限且分布均勻的情況，可以將數據分布到有限數量的桶中，然后從桶中找出Top-K元素。適合特定場景下提高效率。

應用實例

  1. 搜索引擎：在搜索引擎中，為了提供最相關的網頁給用戶，搜索引擎會根據頁面質量、關鍵詞匹配程度等因素對網頁進行評分，然后選擇評分最高的K個網頁展示給用戶。

  2. 推薦系統：電商平臺或社交媒體平臺會根據用戶的瀏覽歷史、購買行為、喜好等數據，計算商品或內容的相關性分數，選出評分最高的K個商品或內容推薦給用戶。

  3. 大數據分析：在處理大規模日志數據時，可能需要找出訪問量最大的K個IP地址、最常見的K個錯誤類型等，以幫助識別異常或優化資源分配。

  4. 金融風控：銀行和金融機構利用Top-K分析來識別潛在的高風險交易，比如監測賬戶中交易額最大的K筆交易，以發現可能的洗錢活動。

Top-K問題因其高效性和實用性，在現代信息技術領域扮演著重要角色。

問題

現在你在面試，面試官要你找出10億得數據中最大得前十個？你該咋找？或許你會說直接用剛才得堆排序，這當然可以。

那假如，面試官讓你用1MB的空間去找這個個數中最大十個嘞？

大家或許就有一點懵逼了吧，哈哈哈

看圖

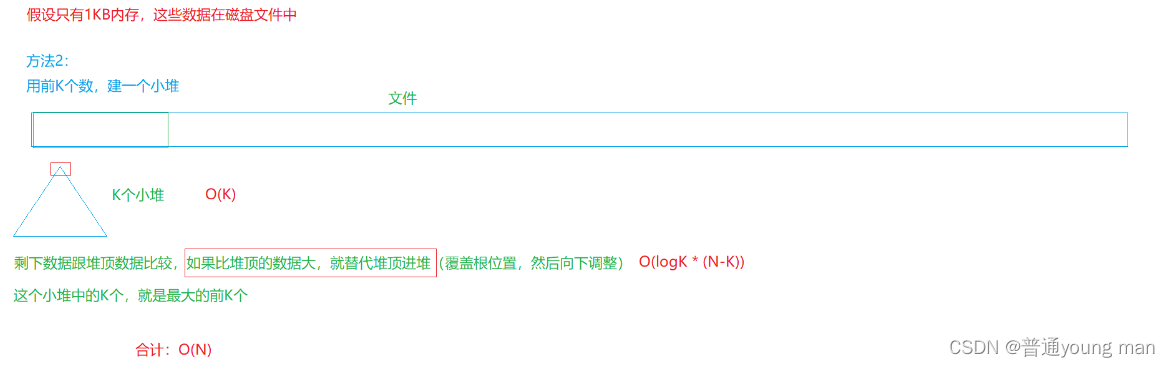
于是我們的代碼就可以這樣寫

//實現創建x(整形)個數據的一個文件，利用1MB空間在x數據中找最大的前n個#include<time.h>
//造數據
void Make_data() {int n = 100000;srand((unsigned int)time(NULL));const char* date = "Date.txt";FILE* write = fopen(date,"w");if (write == NULL){assert("fopen");return;}//將數據寫入文件for (int i = 0; i < n; i++){int ret =  (rand() + i) % n;//+i == 防止重復值，i是不斷變化的，%n == 控制范圍fprintf(write,"%d\n",ret);//將生成的數據不斷的插入 "Date.txt"文件中}fclose(write);
}//建堆
//數據量大
Make_heap() {int n = 0;printf("請輸入你要查看的前幾個數");scanf("%d",&n);//創建一個空間int* New_node = (int*)malloc(n*sizeof(int));if (New_node == NULL){assert("malloc");return;}//將數據從文件中讀出const char* write = "Date.txt";FILE* read = fopen(write,"r");if (read == NULL){assert("fopen");return;}//先把進n個數據for (int i = 0; i < n; i++){fscanf(read,"%d", &New_node[i]);}//建堆sfor (int i = (n-1-1)/2; i >= 0; i--){Downward(New_node,n,i);}//比較剩下的數據依次int end = 0;while (fscanf(read,"%d",&end) > 0)//這里會返回EOF(-1){//判斷if (end > New_node[0]) {//如果end>Newnode[0]位置的數，直接將這個位置的值賦值New_node[0] = end;//再進行向下調整得到小堆Downward(New_node,n,0);}}fclose(read);Heap_qsort_print(New_node,n);
}
Heap_qsort_print(int* p, int n) {//排序：從大到小int new_size = n - 1;while (new_size > 0){Swap(&p[0], &p[new_size]);Downward(p, new_size, 0);--new_size;}//輸出printf("最大的%d個數>: ", n);for (int i = 0; i < n; i++){printf("%d ", p[i]);}
}
int main() {//設置時間戳//Make_data();//建堆Make_heap();}

  1. 生成數據: Make_data 函數生成100,000個整數數據并存儲到一個名為"Date.txt"的文件中。每個數據是通過隨機數生成器得到，并加上循環變量i后取模，以避免重復并控制數據范圍。

  2. 讀取并找出Top-N: Make_heap函數首先詢問用戶想要找出數據文件中的前多少個最大數，然后讀取文件內容，使用最小堆（這里實際實現的是一個簡化版的維護最大值的過程，未完全實現標準的堆結構）來維護當前找到的最大N個數。它先讀取前N個數構建初始“堆”，之后繼續讀取文件中的剩余數據并與堆頂元素比較，若遇到更大的數則替換堆頂元素并重新調整堆。最后，使用Heap_qsort_print函數對維護的N個數進行排序并打印。

  3. 排序及打印: Heap_qsort_print函數實質上是進行了一個非典型的堆排序操作，從堆頂開始每次將堆頂元素（當前最大值）與末尾元素交換，并縮小堆的大小，重復此過程直至整個序列變為降序排列，最后打印出這N個最大的數。

ok今天的博客就結束了哦

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/bicheng/20599.shtml
繁體地址，請注明出處：http://hk.pswp.cn/bicheng/20599.shtml
英文地址，請注明出處：http://en.pswp.cn/bicheng/20599.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

程序員是牛馬嗎？

程序員是牛馬嗎？

在今天的討論中&#xff0c;一個引人深思的問題被提出&#xff1a;程序員是否只是現代社會的牛馬&#xff1f;這個問題迅速引發了激烈的爭論。許多程序員開始意識到&#xff0c;盡管他們辛勤工作&#xff0c;但最終可能仍無法擺脫被剝削的命運。因此&#xff0c;他們渴望改變&a…
閱讀更多...
MySQL(二)-基礎操作

MySQL(二)-基礎操作

一、約束 有時候&#xff0c;數據庫中數據是有約束的&#xff0c;比如 性別列&#xff0c;你不能填一些奇奇怪怪的數據~ 如果靠人為的來對數據進行檢索約束的話&#xff0c;肯定是不行的&#xff0c;人肯定會犯錯~因此就需要讓計算機對插入的數據進行約束要求&#xff01; 約…
閱讀更多...
混合模型方差分析

混合模型方差分析

文章目錄 一、說明二、受試者“間”因素和受試者“內”因素的意思&#xff1f;三、混合模型方差分析回答 3 件事四、混合模型方差分析的假設 一、說明 在本文中&#xff0c;我將討論一種稱為混合模型方差分析的方差分析變體&#xff0c;也稱為具有重復測量的 2 因素方差分析。…
閱讀更多...
音視頻開發_SDL事件處理

音視頻開發_SDL事件處理

今天我為大家介紹一下SDL的事件處理。這里所指的事件處理就是我們通常所說的&#xff0c;鍵盤事件&#xff0c;鼠標事件&#xff0c;窗口事件等。 SDL對這些事件都做了封裝&#xff0c;提供了統一的API&#xff0c;下面我們就來詳細的看一下。 SDL中的事件處理 要想了解 SDL…
閱讀更多...
VB.net進行CAD二次開發（四）

VB.net進行CAD二次開發（四）

netload不能彈出對話框&#xff0c;參考文獻2 參考文獻1說明了自定義菜單的問題&#xff0c;用的是cad的系統命令 只要加載了dll&#xff0c;自定義的命令與cad的命令同等地位。 這時&#xff0c;可以將自定義菜單的系統命令替換為自定義命令。 <CommandMethod("Add…
閱讀更多...
STL-queue的使用及其模擬實現

STL-queue的使用及其模擬實現

在C標準庫中&#xff0c;隊列(queue)是一種容器適配器&#xff0c;它以先進先出的方式組織數據&#xff0c;其中從容器一端插入元素&#xff0c;另一端取出元素。 queue的使用 queue的構造函數 queue的成員函數 empty&#xff1a;檢測隊列是否為空size&#xff1a;返回隊列中有…
閱讀更多...
代碼隨想錄算法訓練營 day23| ● 669. 修剪二叉搜索樹 ● 108.將有序數組轉換為二叉搜索樹 ● 538.把二叉搜索樹轉換為累加樹

代碼隨想錄算法訓練營 day23| ● 669. 修剪二叉搜索樹 ● 108.將有序數組轉換為二叉搜索樹 ● 538.把二叉搜索樹轉換為累加樹

文章目錄 前言669. 修剪二叉搜索樹思路方法一 遞歸法方法二 迭代法 108.將有序數組轉換為二叉搜索樹思路方法一 遞歸法方法二 迭代法 538.把二叉搜索樹轉換為累加樹思路方法一方法二 總結 前言 迭代法都沒看主要是669和538【538很簡單】 669. 修剪二叉搜索樹 思路 不用看教程…
閱讀更多...
【C++刷題】優選算法——位運算

【C++刷題】優選算法——位運算

常見位運算操作總結&#xff1a; 基礎位運算 &&#xff1a;有0則為0 |&#xff1a;有1則為1 ^&#xff1a;相同為0&#xff0c;相異為1 / 無進位相加運算符的優先級 管它什么優先級&#xff0c;加括號就完事兒了給一個數 n&#xff0c;確定它的二進制表示中的第 i (默認是從…
閱讀更多...
【基本數據結構】平衡二叉樹

【基本數據結構】平衡二叉樹

文章目錄 前言平衡二叉樹1 簡介2 旋轉2.1 左旋2.2 右旋2.3 何時旋轉 3 插入節點4 刪除節點5 代碼 參考資料寫在最后 前言 本系列專注更新基本數據結構&#xff0c;現有以下文章&#xff1a; 【算法與數據結構】數組. 【算法與數據結構】鏈表. 【算法與數據結構】哈希表. 【…
閱讀更多...
【斯坦福因果推斷課程全集】1_隨機對照試驗1

【斯坦福因果推斷課程全集】1_隨機對照試驗1

目錄 The average treatment effect Difference-in-means estimation IID Sampling and Population Asymptotics Example: The linear model Regression adjustments with a linear model 隨機對照試驗&#xff08;RCT&#xff09;是統計因果推論的基礎。如果有的話&#…
閱讀更多...
關于FPGA 使用SPI FLASH固化時如何配置固化參數

關于FPGA 使用SPI FLASH固化時如何配置固化參數

關于FPGA 使用SPI FLASH固化時如何配置固化參數 EDA工具&#xff1a;Vivado 關于FPGA 使用SPI FLASH固化時如何配置固化參數一、引言二、如何設置固化參數&#xff1a;使用50M的速度 &#xff0c;SPI為X4 &#xff0c;以及bit壓縮第一&#xff1a;點open implenment design第二…
閱讀更多...
Android之onMeasure的三種模式

Android之onMeasure的三種模式

Overrideprotected void onMeasure(int widthMeasureSpec, int heightMeasureSpec) {super.onMeasure(widthMeasureSpec, heightMeasureSpec);}在 Android 中&#xff0c;onMeasure() 方法是 View 或 ViewGroup 中的一個重要方法&#xff0c;用于測量視圖的大小。在 onMeasure(…
閱讀更多...
安裝軟件缺少dll文件怎么辦，分享多種解決dll問題的方法

安裝軟件缺少dll文件怎么辦，分享多種解決dll問題的方法

在計算機使用過程中&#xff0c;我們經常會遇到安裝軟件時提示缺少dll文件的問題。這種情況通常會導致軟件無法正常運行或啟動。為了解決這個問題&#xff0c;我總結了以下五種方法&#xff0c;希望對大家有所幫助。 一&#xff0c;了解DLL文件是什么 動態鏈接庫&#xff08;D…
閱讀更多...
簡單說說我對集成學習算法的一點理解

簡單說說我對集成學習算法的一點理解

概要 集成學習&#xff08;Ensemble Learning&#xff09;是一種機器學習技術框架&#xff0c;它通過構建并結合多個學習器&#xff08;也稱為個體學習器或基學習器&#xff09;來完成學習任務。 集成學習旨在通過組合多個基學習器的預測結果來提高整體模型的性能。每個基學習…
閱讀更多...
常見儀表盤指示燈的含義，這次夠全了！

常見儀表盤指示燈的含義，這次夠全了！

汽車是當前主要的交通工具之一&#xff0c;給人們的工作、生活提供了便利。大家在學會開車的同時&#xff0c;也得了解一些基本的汽車常識&#xff0c;可以及時的發現車輛的問題&#xff0c;并作出正確的判斷&#xff0c;以此降低車輛的損耗和維修成本。其中最基本的&#xff0…
閱讀更多...
房產證上加名？手把手教你操作，省錢又省心！

房產證上加名？手把手教你操作，省錢又省心！

隨著《民法典》的實施&#xff0c;房產的權屬問題愈發受到重視。夫妻雙方及其親屬常希望能在房產證上增添自己的名字&#xff0c;以保障各自的權益。那么&#xff0c;房產證上到底能寫幾個名字呢&#xff1f;以下是對這一問題的詳細解答。 一、房產證命名無固定限制 在購房時&…
閱讀更多...
準確-K8s系列文章-修改containerd 默認數據目錄

準確-K8s系列文章-修改containerd 默認數據目錄

修改 Kubernetes 集群中 containerd 默認數據目錄為 /data/containerd 前言 本文檔適用于 Kubernetes 1.24 及以上版本的集群，介紹如何將 containerd 默認的數據目錄從 /var/lib/containerd 修改為 /data/containerd。 步驟 1. 停止 containerd 服務（慎重!!!需評估風險！…
閱讀更多...
iOS中的UIScene和UISceneDelegate

iOS中的UIScene和UISceneDelegate

目錄 ???????前言 一、AppDelegate和SceneDelegate的關系 1.AppDelegate 2.SceneDelegate 3.info.plist配置 4.生命周期方法對比 1.應用啟動 2.進入前臺 3.進入后臺 5.何時使用AppDelegate和SceneDelegate 1.AppDelegate 2.SceneDelegate 前言 在iOS 13及之…
閱讀更多...
Linux內核編程入門：深度探索與實戰挑戰

Linux內核編程入門：深度探索與實戰挑戰

Linux內核編程入門&#xff1a;深度探索與實戰挑戰 在操作系統的心臟地帶&#xff0c;Linux內核以其強大、靈活和開源的特性吸引著眾多程序員。對于那些渴望深入了解系統底層機制并親手塑造操作系統的勇士們&#xff0c;Linux內核編程無疑是一個極具挑戰性和吸引力的領域。本文…
閱讀更多...
民國漫畫雜志《時代漫畫》第39期.PDF

民國漫畫雜志《時代漫畫》第39期.PDF

時代漫畫39.PDF: https://url03.ctfile.com/f/1779803-1248636473-6bd732?p9586 (訪問密碼: 9586) 《時代漫畫》的雜志在1934年誕生了&#xff0c;截止1937年6月戰爭來臨被迫停刊共發行了39期。 ps: 資源來源網絡!
閱讀更多...
最新文章

Copyright @ 2022~2023