一、說明

在本文中，我將討論一種稱為混合模型方差分析的方差分析變體，也稱為具有重復測量的 2 因素方差分析。這種統計方法用于分析包括受試者間因素（不同組）和受試者內因素（對同一受試者的重復測量）的數據。

二、受試者“間”因素和受試者“內”因素的意思？

??
受試者間因素和受試者內因素
假設我們想測試不同的教學方法（A、B 和 C）是否會影響學生的表現。我們對 15 名參與者進行研究，每組隨機分配 5 名參與者（每組一種教學方法）。這種設置體現了主題之間的因素。

“受試者間因素”表示研究中的每個參與者只被分配到一組，并且每組經歷不同的情況。

在此分析中，我們的目標是確定各組之間的平均性能水平是否存在顯著差異，這正是單因素方差分析旨在實現的目標。如果您需要更多詳細信息，可以參考我之前的文章，位于“參考資料”部分。

但是，我們可以探索一種教學方法在多個時間點對每個科目的影響，例如：

• 在應用教學方法之前（預測試）
• 教學期過半
• 應用教學方法后（后測）
  這個過程代表了受試者內因素

此過程表示主題內因素。因此，在混合模型方差分析中，我們至少有一個受試者內因子和一個受試者間因子。

?

三、混合模型方差分析回答 3 件事

受試者內因素效應：它確定受試者內因素（前測、中測、后測等時間點）是否對因變量（學生表現）有顯著影響。
受試者間因素效應：它評估了學科間因素（不同的教學方法）是否對因變量有顯著影響。
交互作用：它檢查了受試者內和受試者之間的因素之間是否存在顯著的交互作用。
設置假設
在混合模型方差分析中，通常有三個假設

1/ 受試者內因素（時間）的主效應

原假設 （H0）： 不同測量時間點的平均值沒有顯著差異。
備擇假設 （H1）：不同測量時間點的平均值存在顯著差異。
2/ 學科間因素的主要影響（教學方法）

原假設 （H0）：不同教學方法組的平均值沒有顯著差異。
備擇假設 （H1）： 不同教學方法組的平均值存在顯著差異。
3/ 互動效果（教學方法*時間）：

原假設 （H0）：教學方法對績效的影響不會隨時間而改變（沒有相互作用）。
備擇假設 （H1）： 教學方法對績效的影響會隨著時間而變化（存在交互作用）。

四、混合模型方差分析的假設

1 常態：因變量應近似正態分布在受試者間因子的每一組中。
2 獨立：觀察結果是獨立的。
3 方差的同質性：因變量的方差在受試者間因子的不同組中應該是相等的（我們可以使用 Levene 檢驗來檢查假設，您可以在 參考資料 部分閱讀我關于它的文章
4 無顯著異常值：數據不應包含顯著的異常值，因為它們會不成比例地影響分析結果。
5 協方差的同質性：對于受試者內因素（時間），相關組的所有組合之間的差異方差應相等。（可以使用 Mauchly 的球形度測試進行測試，以后可以調整）
關于協方差的同質性的注意事項：在我們的例子中，我們有 3 個組。
第一組之間的差異。
第二組的差異，第一組和第三組的差異。
第二組和第三組之間的差值應具有相同的方差。

1/ 數據 ：讓我們計算一下前面的例子。我將利用 Numpy 生成隨機數據。
?

import pandas as pd
import numpy as np
from pingouin import mixed_anovanp.random.seed(0)n = 15time_points = ['T1', 'T2', 'T3']data = pd.DataFrame({'Participant': np.repeat(range(1, n+1), len(time_points)),'Teaching_Method': np.repeat(['A', 'B', 'C'], n),'Time': np.tile(time_points, n),'Score': np.random.randint(50, 100, size=n*len(time_points))
})data.head()

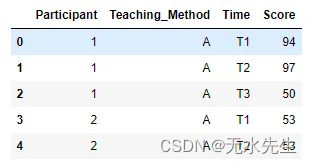
2/ 假設：

A/ 正態性 ： 現在，我們需要驗證這些假設。我將首先使用 Shapiro-Wilk 檢驗檢查正態性

注意：

• 原假設 （H0） 是數據服從正態分布。
• 如果 p 值大于所選的顯著性水平，則我們無法否定原假設。這表明沒有重要證據可以得出數據偏離正態分布的結論。

from scipy.stats import shapirofor method, group_data in data.groupby('Teaching_Method')['Score']:stat, p = shapiro(group_data)print(f'Shapiro-Wilk test for {method}: p-value = {p}')# Shapiro-Wilk test for A: p-value = 0.3026245223583117
# Shapiro-Wilk test for B: p-value = 0.5795532845153779
# Shapiro-Wilk test for C: p-value = 0.7610549007614936

由于在所有教學方法的 Shapiro-Wilk 檢驗中，所有 p 值都大于 0.05（我使用的顯著性水平），這表明沒有明顯證據表明偏離正態性。因此，滿足正態性假設。

B/ 方差的同質性：為了評估方差的同質性，我將采用 Levene 檢驗。

from scipy.stats import levenestat, p = levene(*[group_data for method, group_data in data.groupby('Teaching_Method')['Score']])
print(f'Levene\'s test for homogeneity of variances: p-value = {p}')
# Levene's test for homogeneity of variances: p-value = 0.8937735564168452

注意：

Levene檢驗中的原假設（H0）是被比較組的方差相等。
由于 Levene 檢驗的 p 值為 0.89（大于顯著性水平），因此我們無法否定原假設，表明沒有顯著證據表明教學方法組之間的方差存在顯著差異。

C/ 協方差的齊質性：如前所述，我們可以利用 Mauchly 測試來實現此目的。

from pingouin import sphericitysphericity_test = sphericity(data, dv='Score', subject='Participant', within='Time')print(sphericity_test)
# SpherResults(spher=True, W=0.9298475348159647, chi2=0.9455504153256469, dof=2, pval=0.6232701617877808)

注意：

• 原假設 （H0） 是所有可能的受試者內條件對之間的差異方差相等。
  “spher=True” 參數表示滿足球形度的假設。此外，當觀察 p 值（大于 alpha）時，有大量證據拒絕球形度的假設。

D/ 異常值 ：我們可以采用Tukey的方法（Tukey的柵欄，Tukey的規則），它涉及以下步驟：

計算數據的四分位距 （IQR），即第三個四分位數 （Q3） 和第一個四分位數 （Q1） 之間的差值。您也可以在“參考資料”部分參考我關于它的文章。
將下圍欄 （LF） 定義為 Q1–1.5 * IQR，將上圍欄 （UF） 定義為 Q3 + 1.5 * IQR。任何低于下圍欄或高于上圍欄的數據點都被視為潛在的異常值。
注意： 對于異常值數顯著的閾值，沒有一般規則，因為它可能取決于多個因素。

import seaborn as sns
import matplotlib.pyplot as pltQ1 = data['Score'].quantile(0.25)
Q3 = data['Score'].quantile(0.75)
IQR = Q3 - Q1lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQRoutliers = data[(data['Score'] < lower_bound) | (data['Score'] > upper_bound)]print("Outliers:")
print(outliers)plt.figure(figsize=(8, 6))
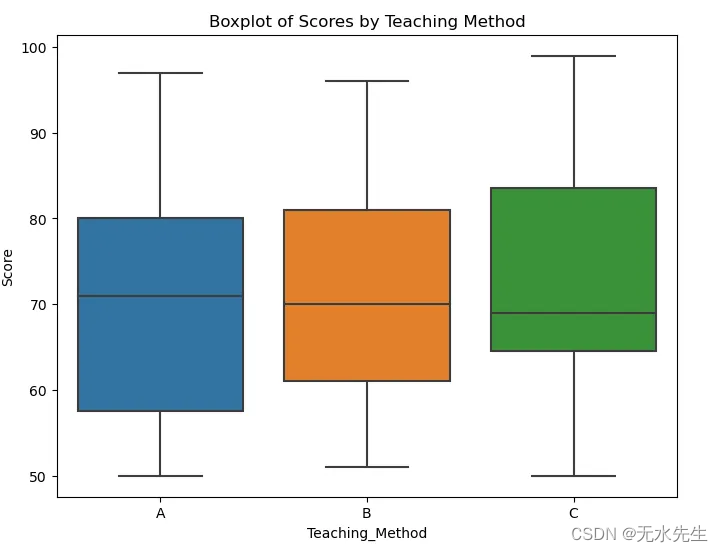
sns.boxplot(x='Teaching_Method', y='Score', data=data)
plt.title('Boxplot of Scores by Teaching Method')
plt.show()# Outliers:
# Empty DataFrame
# Columns: [Participant, Teaching_Method, Time, Score]
# Index: []

3/ 讓我們運行測試： 現在我們已經確認滿足了假設，我們可以繼續進行測試。

anova = mixed_anova(dv='Score', within='Time', between='Teaching_Method', subject='Participant', data=data)print(anova)

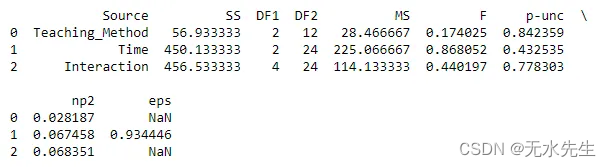
讓我們分析每個假設：

1/ 時間的主要影響：由于 p 值 （0.432535） 大于 0.05，我們無法否定原假設。這意味著沒有重要證據表明時間對分數有重大影響。

2/ 教學方法的主要效果：同樣，由于 p 值 （0.842359） 大于 0.05，我們無法否定原假設。沒有重要證據表明教學方法對分數有顯著影響。

3/ 交互效果：同樣，由于 p 值 （0.778303） 大于 0.05，我們無法否定原假設。沒有顯著的證據表明教學方法和時間對分數之間存在交互作用。

注意：

效應大小 （ηp2） 和 Epsilon （ε） ：

效應大小（ηp2）值較小，表明自變量解釋的方差比例相對較低。
Epsilon （ε） 提供有關可能違反球形的信息。然而，由于我們已經用 Mauchly 檢驗證實了球形度，因此 epsilon 值在這里是補充的。
如果您希望我們涵蓋特定主題，請隨時告訴我！您的意見將有助于塑造我的內容的方向，并確保它保持相關性和吸引力