1. 概念

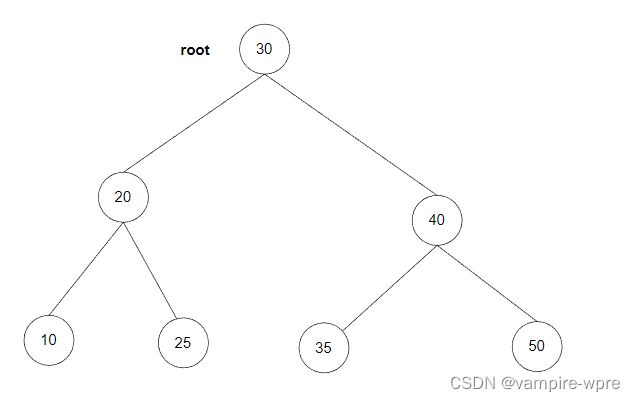
二叉搜索樹是特殊的二叉樹,也叫二叉排序樹,它的特點是:每個結點的左子樹上的所有結點的值都小于這個結點的值,右子樹上的所有結點的值都大于這個結點的值,另外所有的左子樹和右子樹也分別為二叉搜索樹,如圖:

2. 二叉搜索樹的操作

2.1 查找

根據二叉搜索樹的性質來,很容易可以理解查找的邏輯:從根結點開始,比較結點的值與待查找的值,如果待查找的值比根結點的值小,說明待查找的結點一定在樹的左邊,如圖

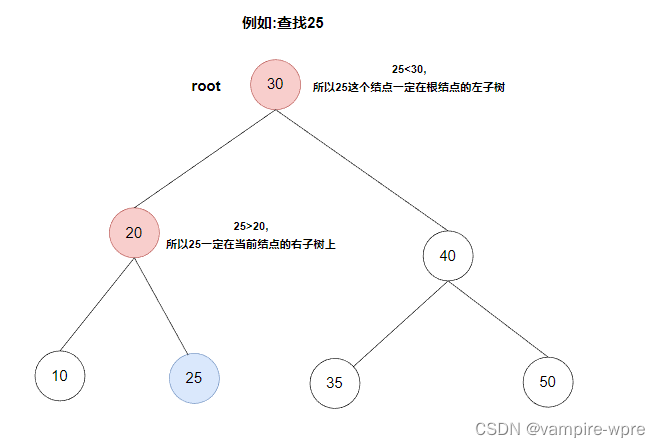
當然也有其他情況:根結點為空、該樹不存在要查找的這個結點,這個時候直接返回null就可以了

public TreeNode search(int key) {TreeNode cur = root;while (cur != null) {if (cur.val > key) {cur = cur.left;} else if (cur.val < key) {cur = cur.right;} else {return cur;}}return null;
}

2.2 插入

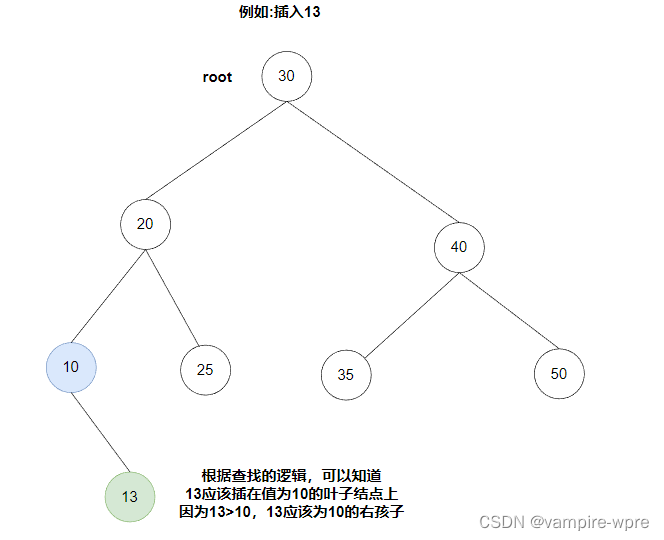
插入的前提:插入一定是在葉子結點上插入,因為插入之后也要滿足二叉搜索樹的性質,插入之前需要查找要插入的位置,而查找的邏輯和剛才的邏輯一樣

2.3 刪除

刪除的情況比較復雜,主要分為以下情況(假設del為要刪除的結點,parent為del的父親結點):

1、cur.left == null

• 1、del 是root
• 2、del 不是root，del是parent.left
• 3、del 不是root，del是parent.right

2、cur.right == null

• 1、del 是root
• 2、del 不是root，del是parent.left
• 3、del 不是root，del是parent.right

3、cur.left != null && cur.right != null

下面我們一個一個分析
情況1：del.left==null

• 情況1.1：del是根結點root，刪除邏輯：root =del.right
  

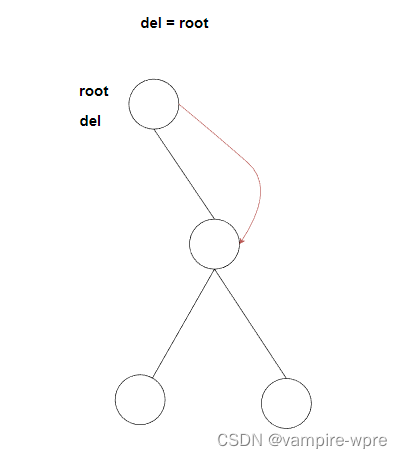
• 情況1.2 ：del不是根結點，del是parent.left刪除邏輯：parent.left=del.right
  

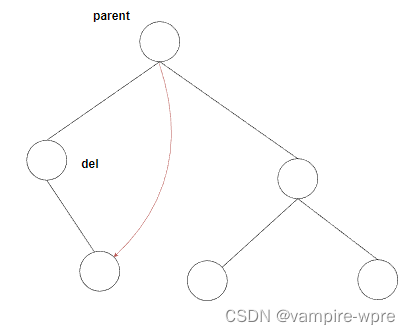
• 情況1.3：del不是根結點,del是parent.right，刪除邏輯：parent.right=del.right
  
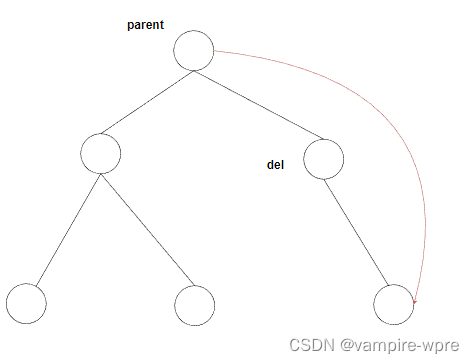
  情況2：del.right==null

• 情況2.1：del是根結點root，刪除邏輯root = del.left
  

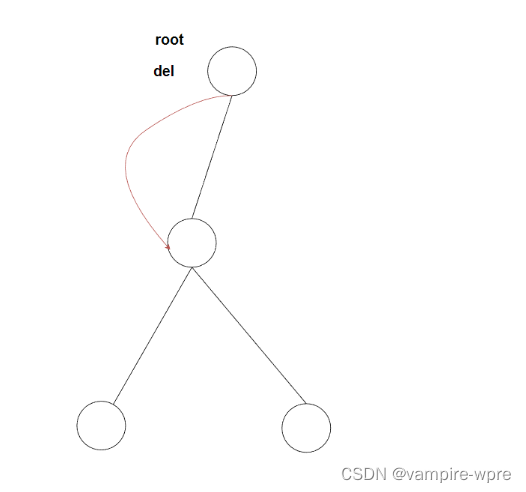
• 情況2.2：del不是根結點,del是parent.left，刪除邏輯：parent.left = del.left
  

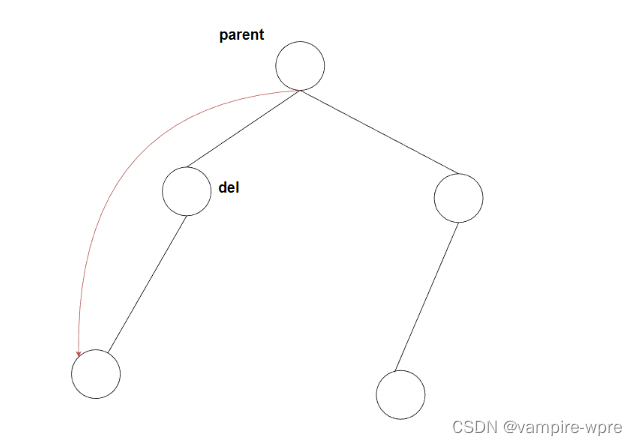
• 情況2.3：del不是根結點,del是parent.right，刪除邏輯：parent.right = del.left
  
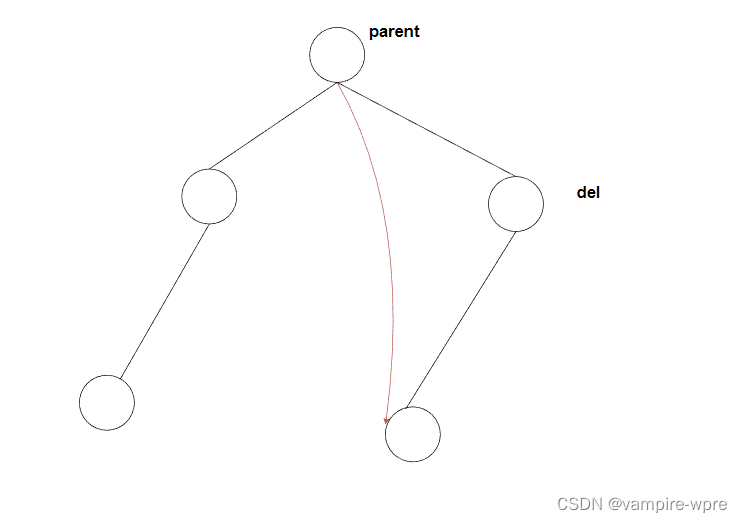
  情況3：要刪除的結點左右都不為空
  如圖
  

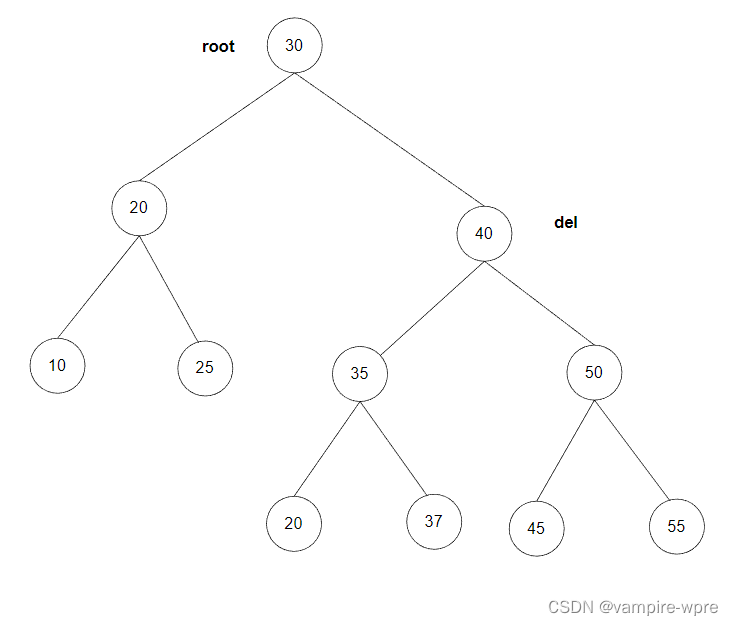
兩種方法：
1.找到del的左樹找值最大的結點，將del結點的值替換成這個值，接著刪除這個最大值的結點，如上圖的37，刪除之后的情況如下

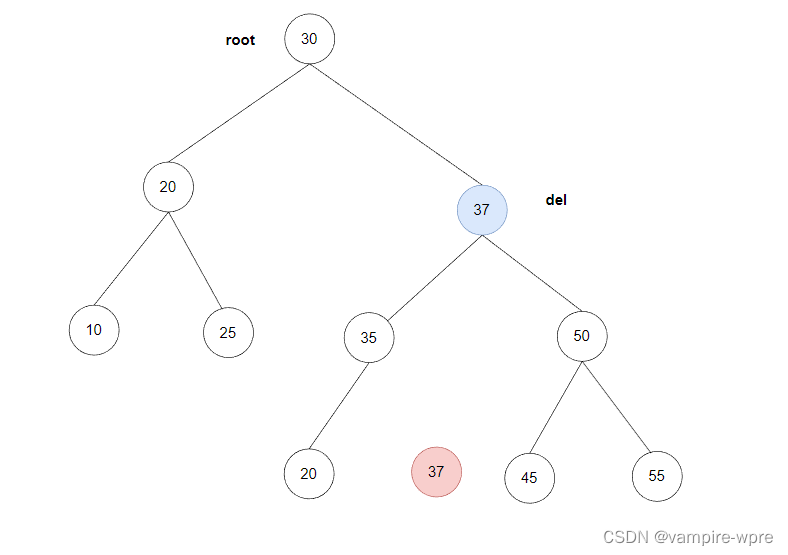
2.找到del的右子樹找值最小的結點，將del結點的值替換成這個值，接著刪除這個最小值的結點，如上圖的45，刪除之后的結果如下

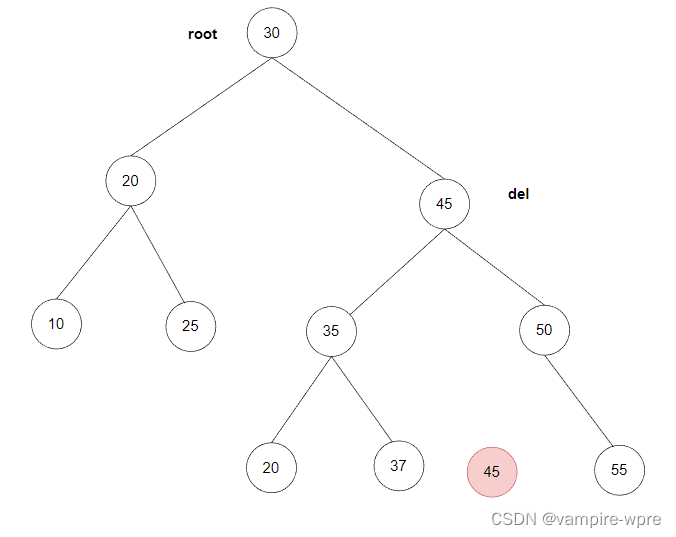
3. 全部代碼

public class BinarySearchTree {static class TreeNode {int val;TreeNode left;TreeNode right;public TreeNode(int val) {this.val = val;}}public TreeNode root;/*** 查找** @return*/public TreeNode find(int key) {TreeNode cur = root;while (cur != null) {if (cur.val > key) {cur = cur.left;} else if (cur.val < key) {cur = cur.right;} else {return cur;}}return null;}//插入public void insert(int key) {TreeNode cur = root;TreeNode parent = null;TreeNode newNode = new TreeNode(key);if (cur == null) {root = newNode;return;}while (cur != null) {if (cur.val > key) {parent = cur;cur = cur.left;} else if (cur.val < key) {parent = cur;cur = cur.right;} else {return;}}if (parent.val > key) {parent.left = newNode;} else {parent.right = newNode;}}//刪除public void delete(int key) {TreeNode cur = root;TreeNode parent = null;while (cur != null) {if (key > cur.val) {parent = cur;cur = cur.right;} else if (key < cur.val) {parent = cur;cur = cur.left;} else {//刪除結點remove(parent, cur);return;}}}// 分情況討論private void remove(TreeNode parent, TreeNode del) {//情況1:del.left==nullif (del.left == null) {//情況1.1 del是rootif (del == root) {root = del.right;} else {if (del == parent.left) {//情況1.2 del不是root,del是parent.leftparent.left = del.right;} else if (del == parent.right) {//情況1.3 del不是root,del是parent.rightparent.right = del.right;}}} else if (del.right == null) {//情況2:del.right==nullif (del == root) {//情況2.1 del是rootroot = del.left;} else {if (del == parent.left) {//情況2.2 del是parent.leftparent.left = del.left;} else if (del == parent.right) {//情況2.3 del是parent.rightparent.right = del.left;}}} else {//情況3 del.left和del.right都不為空//將del右樹的值最小的結點或者左樹的值最大的結點和del替換//右邊找TreeNode target = del.right;TreeNode targetP = del;while (target.left != null) {targetP = target;target = target.left;}//刪除之前先交換del.val = target.val;//分情況刪除if (target == targetP.right) {targetP.right = target.right;}if (target == targetP.left) {targetP.left = target.right;}}}
}