兩個雙指針的 “他“和“ 她“會相遇么？ —

本篇會加入個人的所謂魚式瘋言

??????魚式瘋言:??????此瘋言非彼瘋言
而是理解過并總結出來通俗易懂的大白話,
小編會盡可能的在每個概念后插入魚式瘋言,幫助大家理解的.
🤭🤭🤭可能說的不是那么嚴謹.但小編初心是能讓更多人能接受我們這個概念 ！！！

在這里插入圖片描述

前言

因為小編最近在學習算法，每次學習新知識，都會有新的體會和心得，就會和小伙伴們一起分享，今天帶來我們算法首篇 ————“雙指針” 算法 💥💥💥

這時就會有小伙伴問了，我們的"雙指針"算法不是在 “題海尋offer” 專題中講解過么？為啥還要重復學習呢 🤔 🤔 🤔

是的，但這次小編帶來的是更重點更詳細并且更系統以算法的角度一步一步講解我們的 “雙指針” 算法 💖 💖 💖

一. 雙指針初識

1. 雙指針算法的認識

首先小編在這里得區別一個概念

這里我們提及的雙“指針” 的指針并不是我們學過 C語言的定義 int * p = &a 那個指針，

這里我們用的指針其實就是一個變量

我們通過 變量 來指向一個元素然后不斷移動來影響數據的一個單純的變量

而 雙指針 就是定義兩個變量來影響數據

2. 雙指針算法的種類

常見的雙指針有兩種形式：

一種是 對撞指針，一種是 左右指針。

對撞指針

? 對撞指針 從兩端向中間移動。一個指針從 最左端 開始，另一個從 最右端 開始，然后逐漸往中間逼近。

? 對撞指針 的終止條件一般是兩個指針相遇=或者錯開（也可能在循環內部找到結果直接跳出循環），也就是：

? left == right （兩個指針指向同一個位置）

? left > right （兩個指針錯開）

快慢指針

快慢指針：又稱為龜兔賽跑算法，其基本思想就是使用兩個移動 速度不同 的指針在數組或鏈表等序列結構上移動。

這種方法對于處理 環形鏈表 或 數組 非常有用。

其實不單單是環形鏈表或者是數組，如果我們要研究的問題出現循環往復的情況時，均可考慮使用 快慢指針 的思想。

快慢指針的實現方式有很多種，最常用的一種就是：

在一次循環中，每次讓慢的指針向后移動 一位 ，而快的指針往后移動 兩位，實現一快一慢。

魚式瘋言

總結三句話

指針本質上是 變量, 只是形式上我們俗稱 “指針”
對撞指針是從起點和終點兩個同時相向走，會相遇 的兩個指針
快慢指針是 同向不相遇的兩個走的跨度不一樣的指針

二. 雙指針的算法運用

1. 復寫零

1089.復寫零題目鏈接

<1> . 題目描述

在這里插入圖片描述

給你一個長度固定的整數數組 arr ，請你將該數組中出現的每個零都復寫一遍，并將其余的元素
向右平移。
注意：請不要在超過該數組長度的位置寫入元素。請對輸入的數組就地進行上述修改，不要從函數返
回任何東西。
示例 1：
輸入： arr = [1,0,2,3,0,4,5,0]
輸出： [1,0,0,2,3,0,0,4]
解釋：
調用函數后，輸入的數組將被修改為： [1,0,0,2,3,0,0,4]

題目的含義：

在這個數組中，我們從左往右，每出現一個0 就在右邊位置再寫一個 0 ，然后數據一直 挪動 , 原有數據就要一直往右 挪動

<2>. 講解算法原理

大體思路分為：

如果 「從前向后」 進行原地復寫操作的話，由于 0 的出現會復寫兩次，導致沒有復寫的數「被覆
蓋掉」。因此我們選擇「從后往前」的復寫策略。

但是「從后向前」復寫的時候，我們需要找到 `「最后一個復寫的數」 `` ，因此我們的大體流程分兩
步：

算法流程

先找到最后一個復寫的數

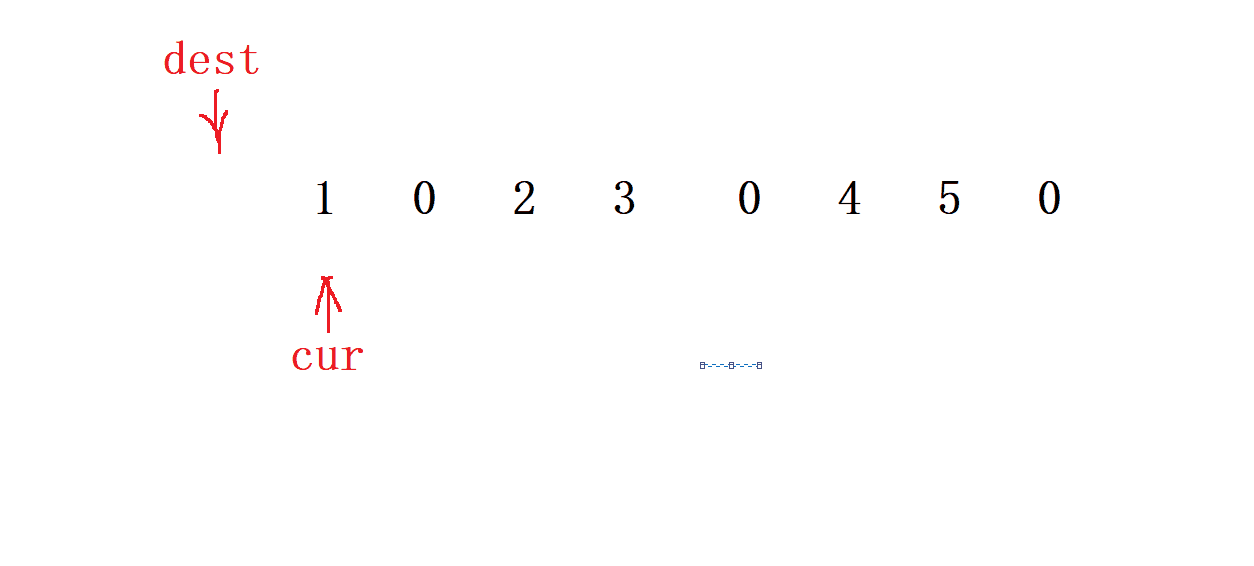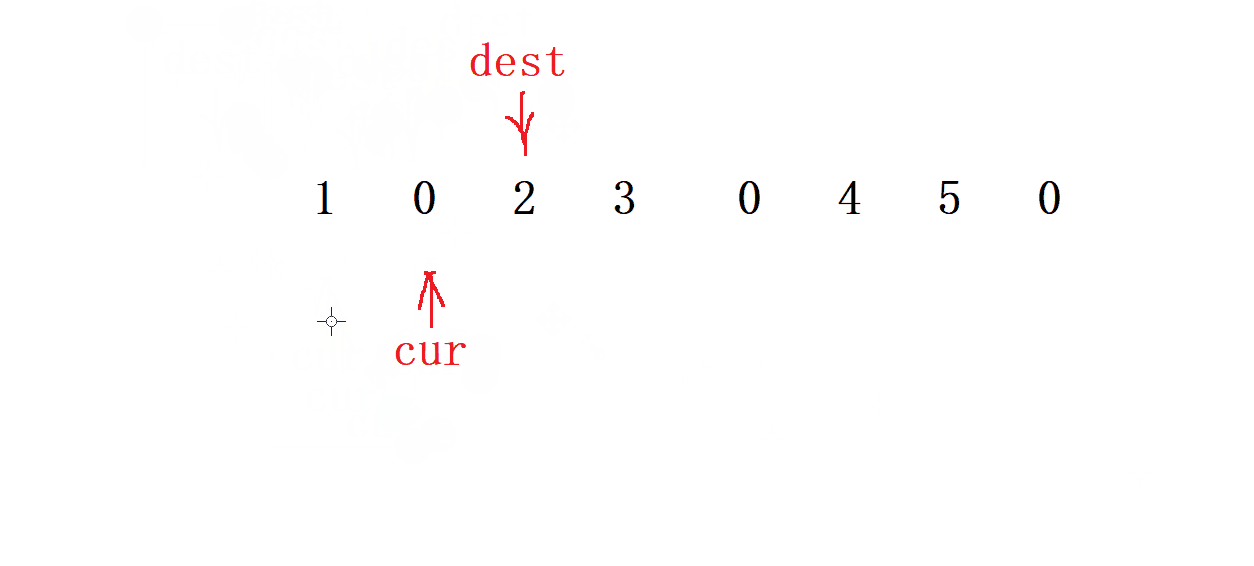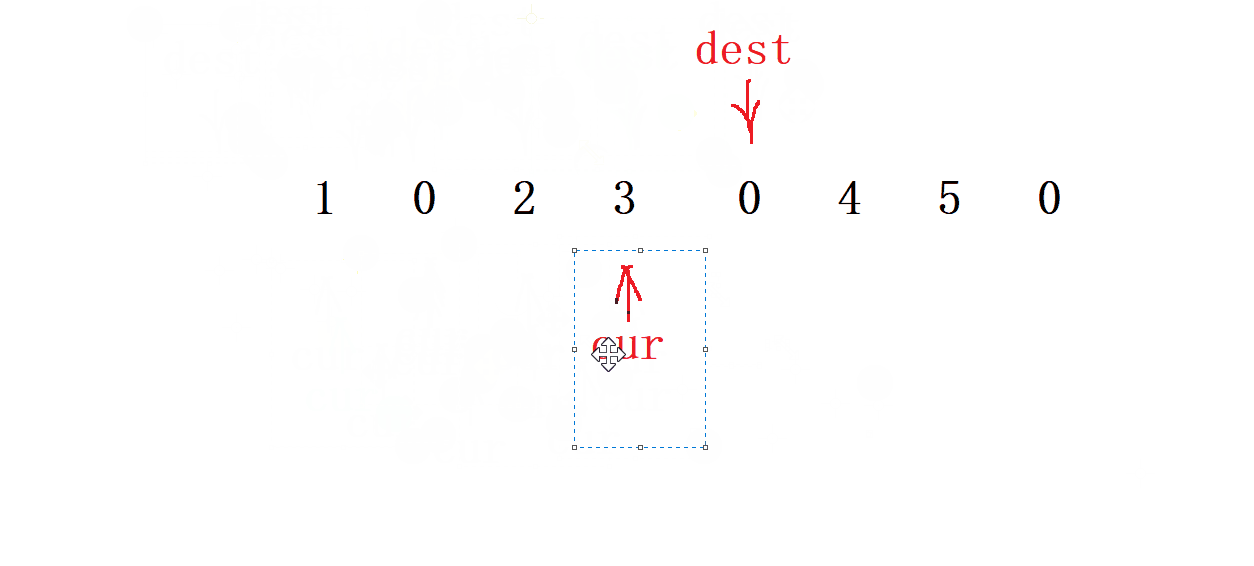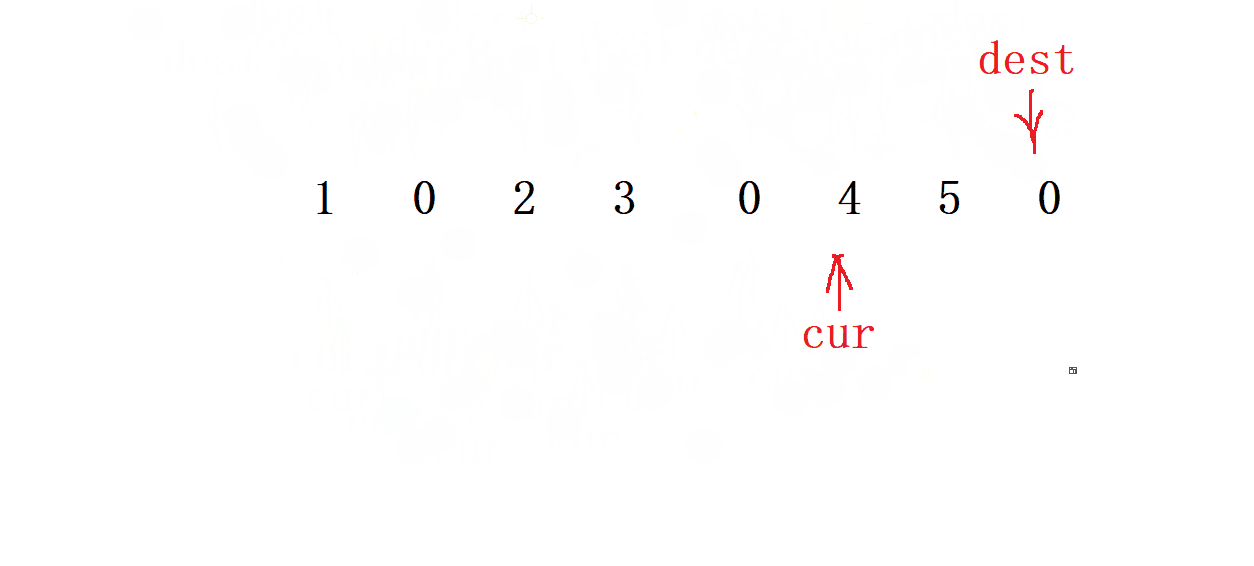
請添加圖片描述

先定義一個 cur=0 和 dest= -1 指針來通向移動

先讓 cur 向前走一步，當 cur 位置遇到值為 0 時就 dest 就走兩步

3,否則讓 dest 走一步，直到 dest 到底數組下標 >= n- 1 的位置就停止

然后從后向前進行復寫操作。

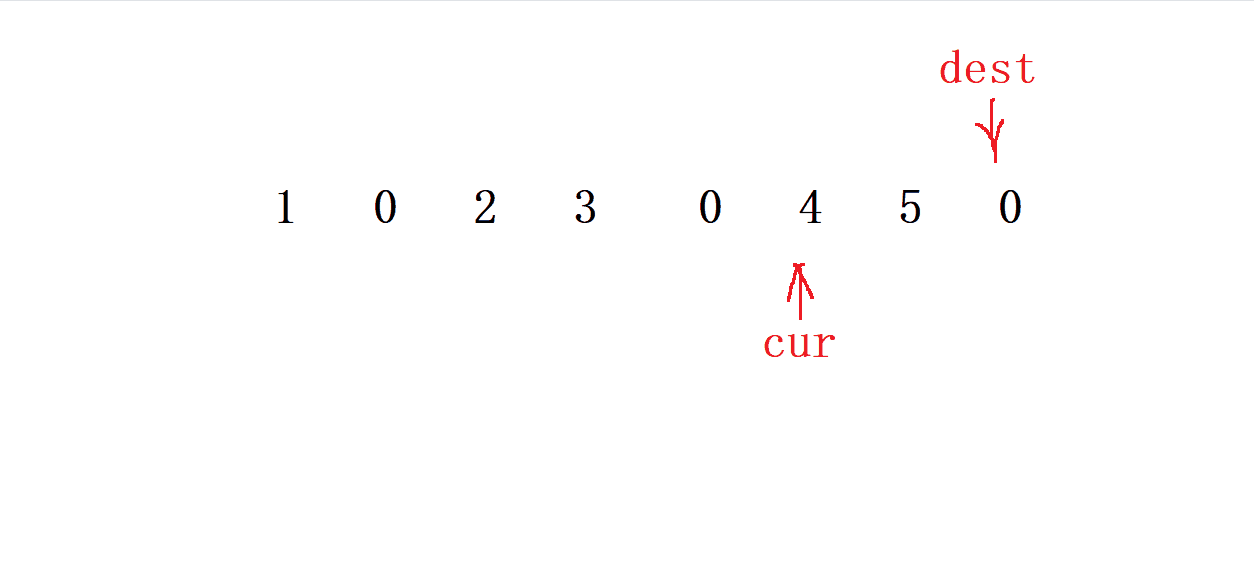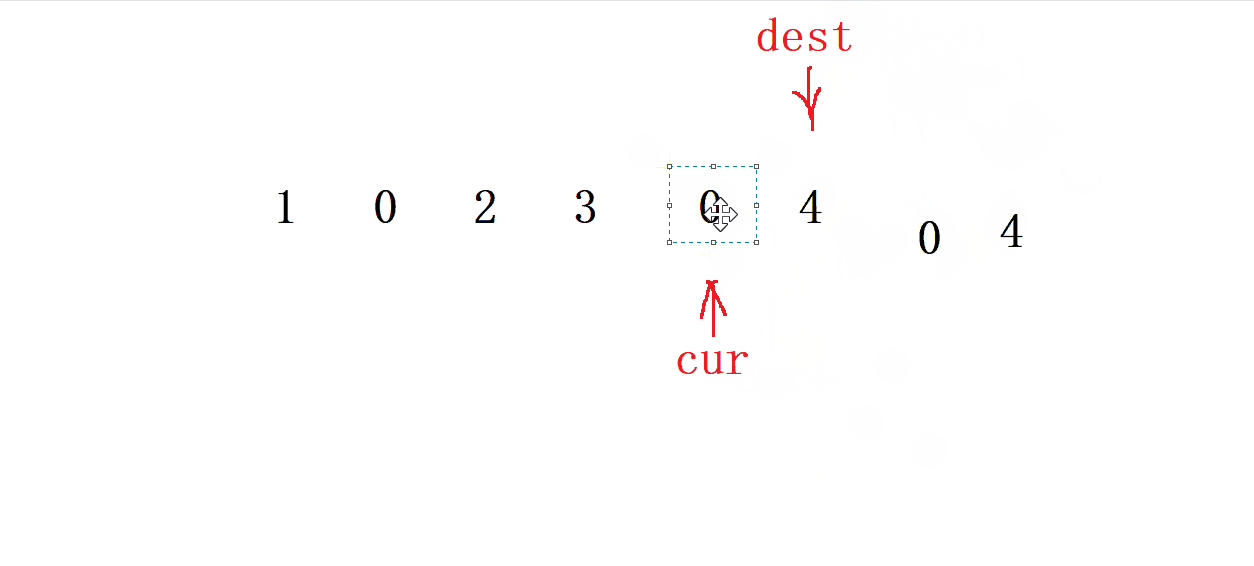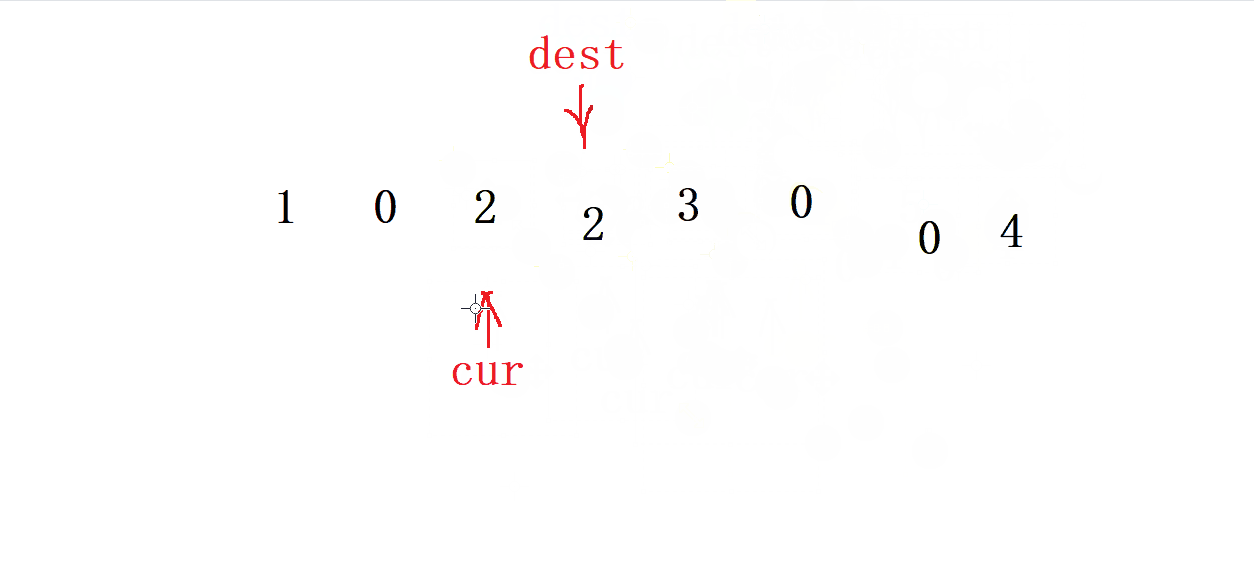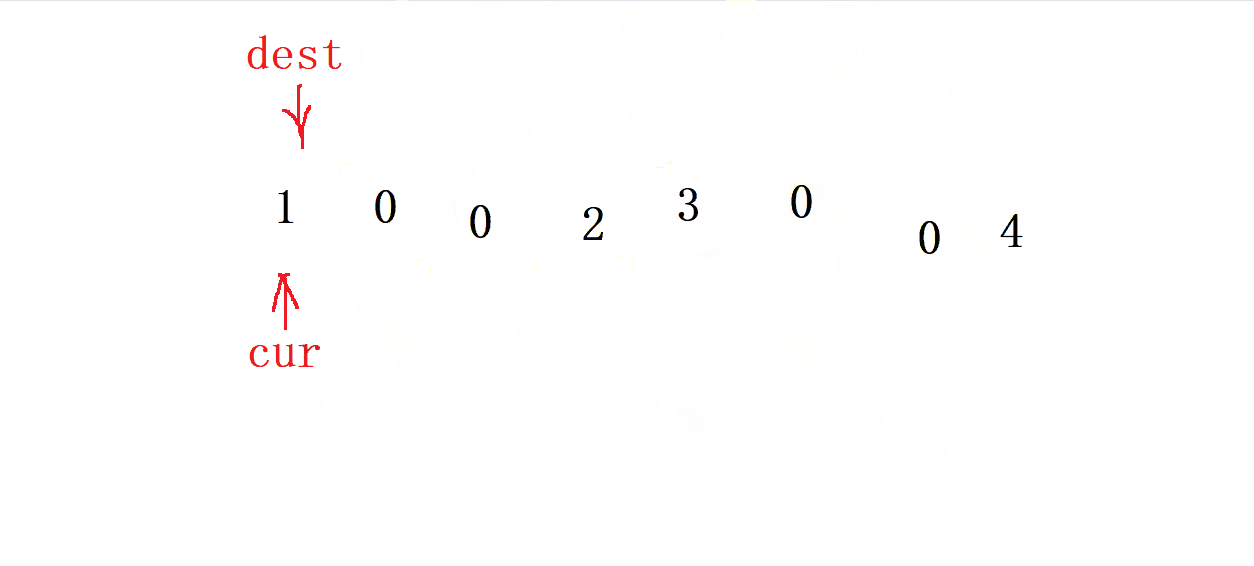
請添加圖片描述

當 cur 遇到 0 時，就讓 dest 跳躍兩次并把這兩次的值都賦值為 0 ， cur 走一步

當 cur 不是 0 時，就把 cur 的值賦給 dest , 接著讓 dest 和 cur 都走一步

<3>. 編寫代碼

class Solution {public static void duplicateZeros(int[] arr) {int cur=0;int dest=-1;int n=arr.length;while (cur < n) {if (arr[cur]==0) {dest +=2;} else {dest++;}if (dest >= n-1) {break;}cur++;}if (dest > n-1) {arr[n-1]=0;cur--;dest-=2;}while (cur >= 0) {if (arr[cur]==0) {arr[dest--]=0;arr[dest--]=0;cur--;} else {arr[dest--]=arr[cur--];}}}}

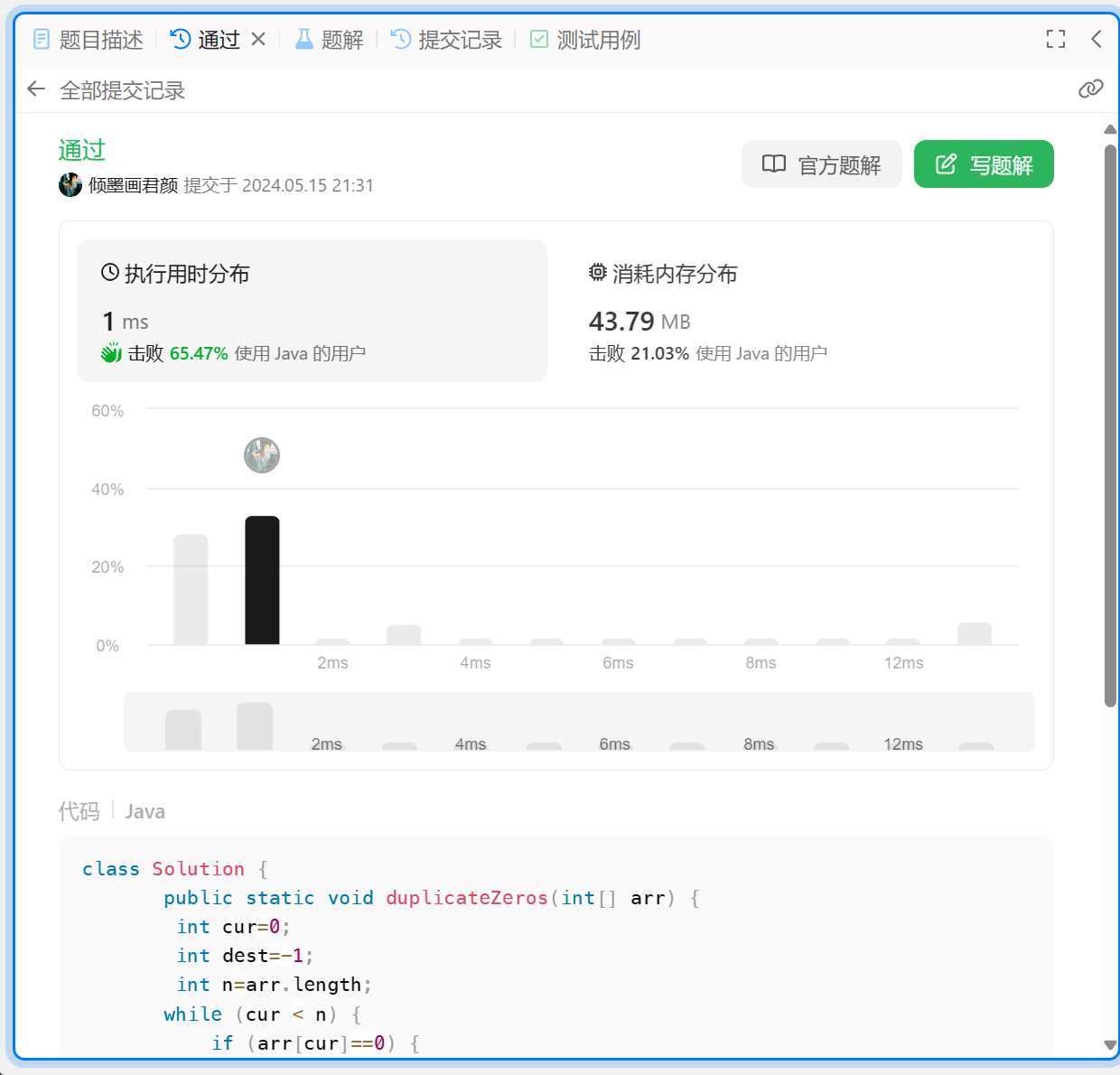
在這里插入圖片描述

魚式瘋言

說兩句小編關于本題自己的理解和體會

這里我們用到了前后指針（快慢指針），一個 快指針 模擬復寫零后的數組的位置，而 慢指針 用于模擬 == 未復寫零后的數組的最后一個元素的位置

細節：

   if (dest > n-1) {arr[n-1]=0;cur--;dest-=2;}

當 == dest== 的位置跳到 n 的位置時，說明 0 的位置不夠放，我們就需要把最后一個位置賦值為 0 ，
并讓 dest 想左走兩步， cur 走一步即可

2. 快樂數

202. 快樂數題目鏈接

<1>. 題目描述

在這里插入圖片描述

編寫一個算法來判斷一個數 n 是不是快樂數。

「快樂數」定義為：

? 對于一個正整數，每一次將該數替換為它每個位置上的數字的平方和。

? 然后重復這個過程直到這個數變為 1，也可能是無限循環但始終變不到 1 。

? 如果這個過程結果為 1 ，那么這個數就是快樂數。

? 如果 n 是快樂數就返回 true ；不是，則返回 false 。

示例 1：
輸入： n = 19
輸出： true
解釋：
19 -> 1 * 1 + 9 * 9 = 82
82 -> 8 * 8 + 2 * 2 = 68
68 -> 6 * 6 + 8 * 8 = 100
100 -> 1 * 1 + 0 * 0 + 0 * 0 = 1

示例 2：
輸入： n = 2
輸出： false
解釋：（這里省去計算過程，只列出轉換后的數）
2 -> 4 -> 16 -> 37 -> 58 -> 89 -> 145 -> 42 -> 20 -> 4 -> 16

往后就不必再計算了，因為出現了重復的數字，最后結果肯定不會是1

題目含義：

讓一個數一直取出每個位置上的數字的 平方算出他們的之和 ，得到這個數后判斷是否為 1

如果為 1 說明是快樂數返回 true

如果繼續循環的按照上面的方法計算知道得到看是否最終結果為 1= ，若不是就返回 false

<2>. 講解算法思想

我們先簡單的分析一下

為了方便敘述，將「對于一個正整數，每一次將該數替換為它每個位置上的數字的平方和」這一個
操作記為 x 操作；

題目告訴我們，當我們不斷重復 x 操作的時候，計算一定會「死循環」，死的方式有兩種：

? 情況一：一直在 1 中死循環，即 1 -> 1 -> 1 -> 1…

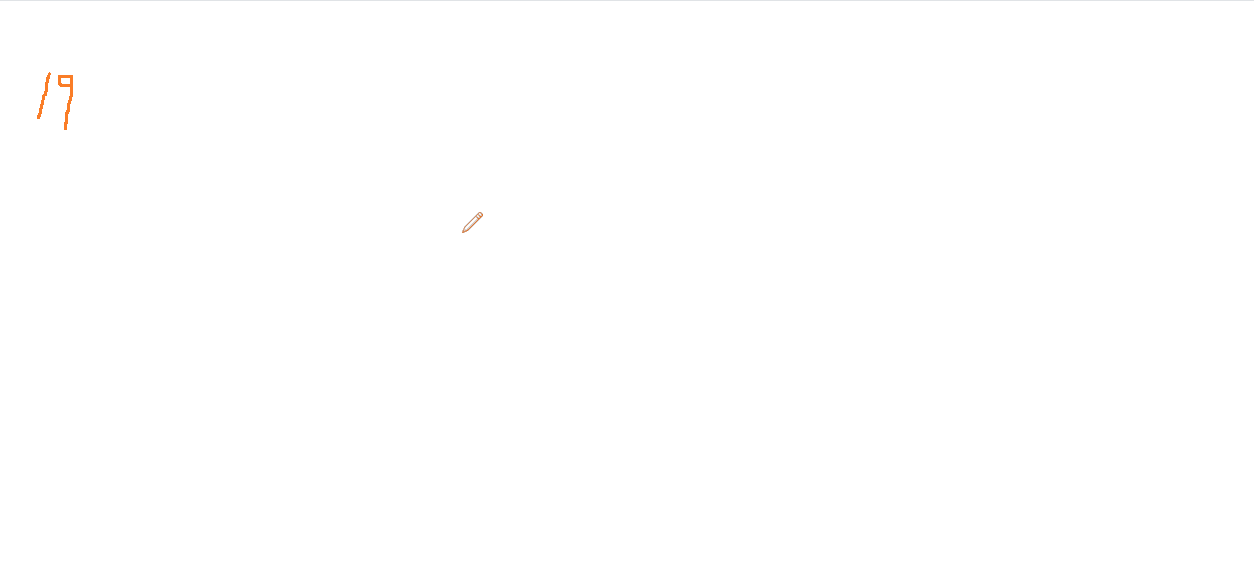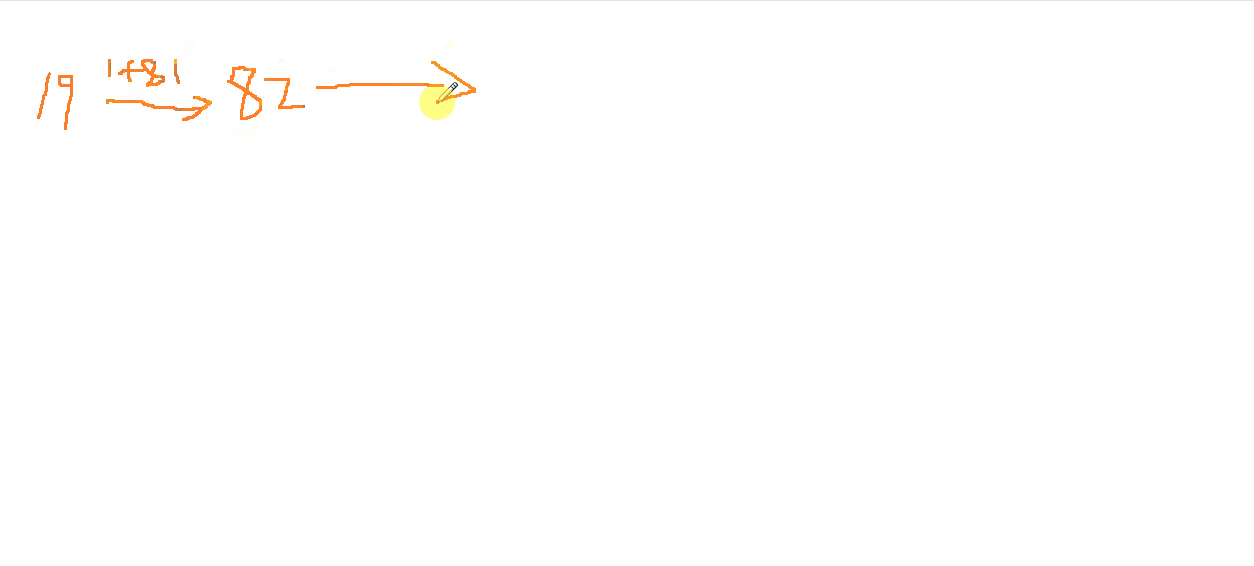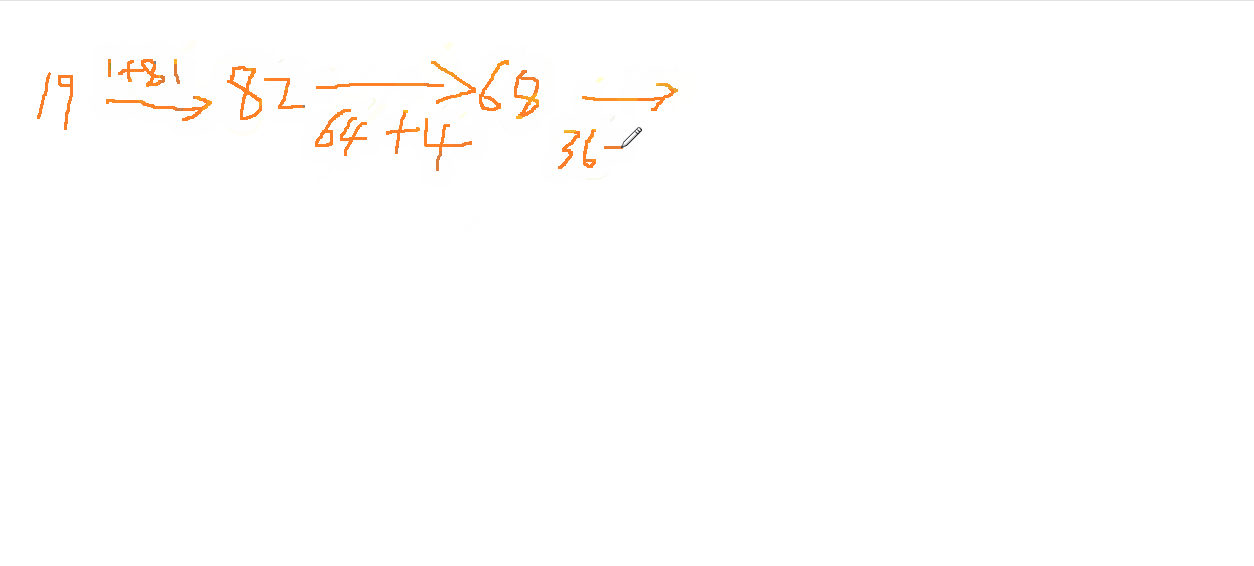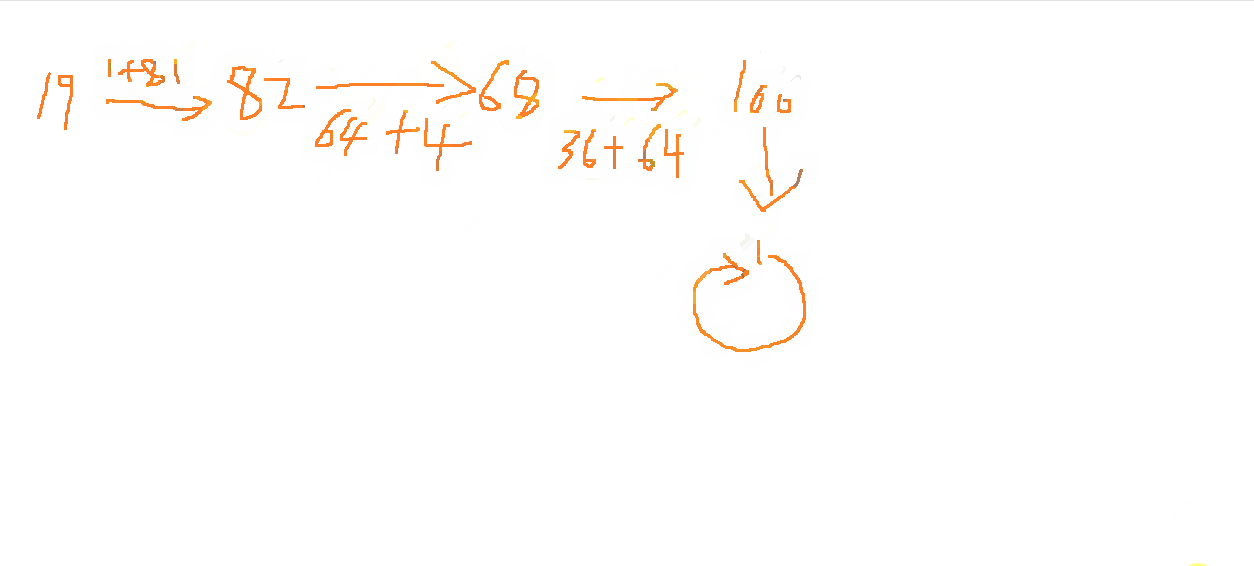
請添加圖片描述

? 情況二：在歷史的數據中死循環，但始終變不到 1

請添加圖片描述

由于上述兩種情況只會出現一種

因此，只要我們能確定循環是在「情況一」中進行

還是在 「情況二 ] 中進行，就能得到結果。

大體的算法思想

先用一個方法來獲取到每一位上數字的平方之和

由于我們在循環內查找這個數 (相當于檢查一個鏈表是否成環) ，所以我們第一步考慮的應該是快慢指針的思維，

我們進行利用定義一個 left 的單位為 1 走一步，再定義一個 right 單位為 2 走兩步 ,因為是環形所以 最終是一定會相遇的

最后一步 我們只需要在相遇的位置判斷是否是等于 1 即可

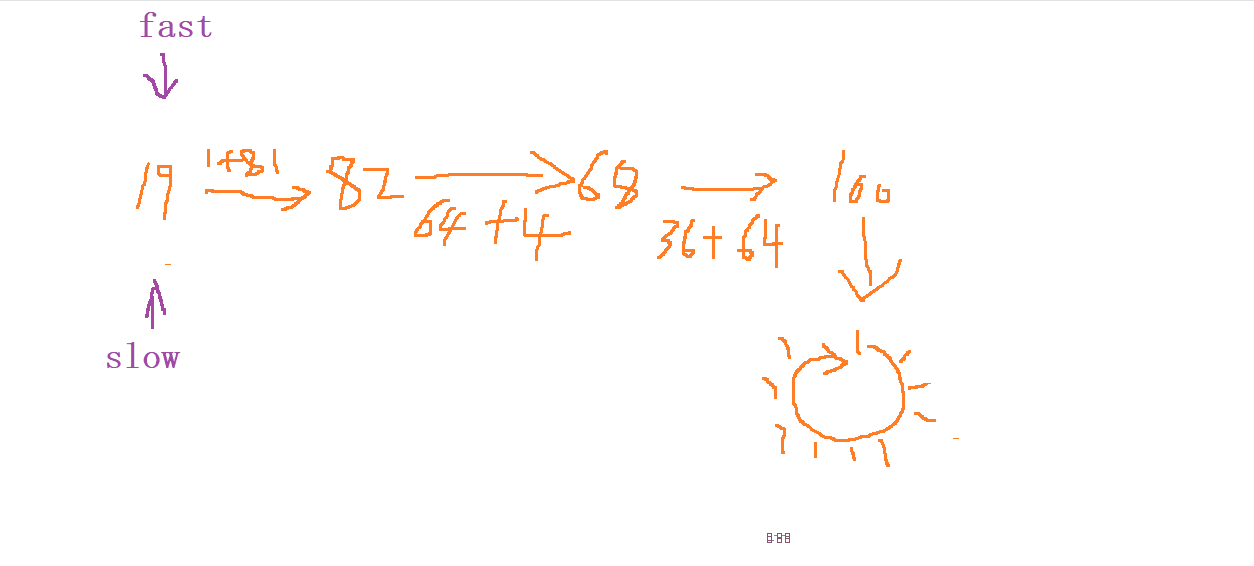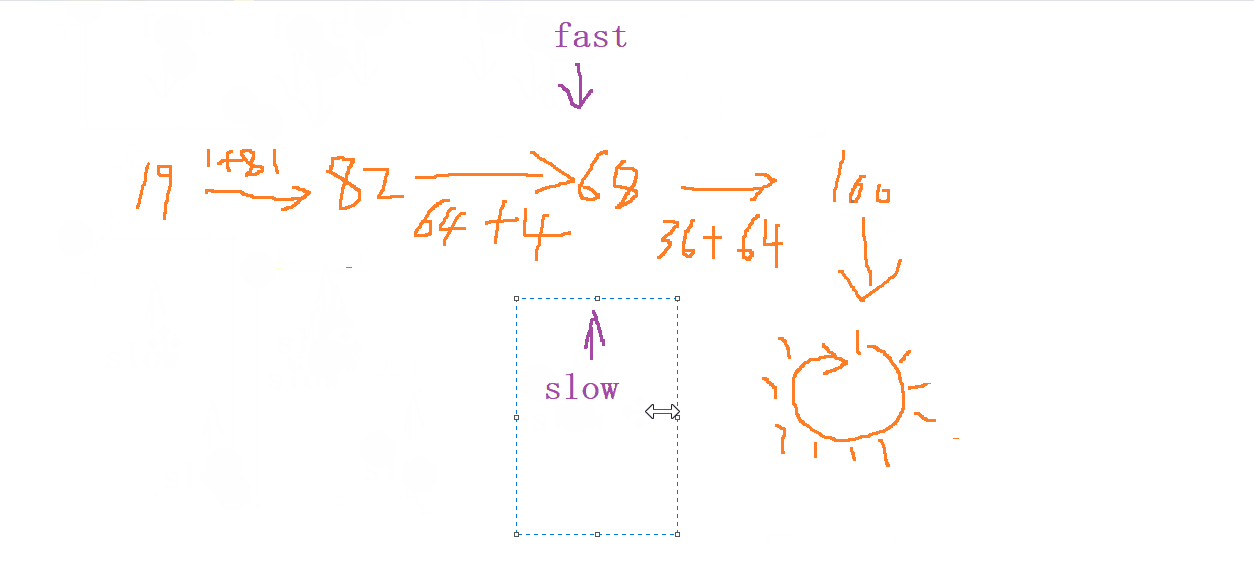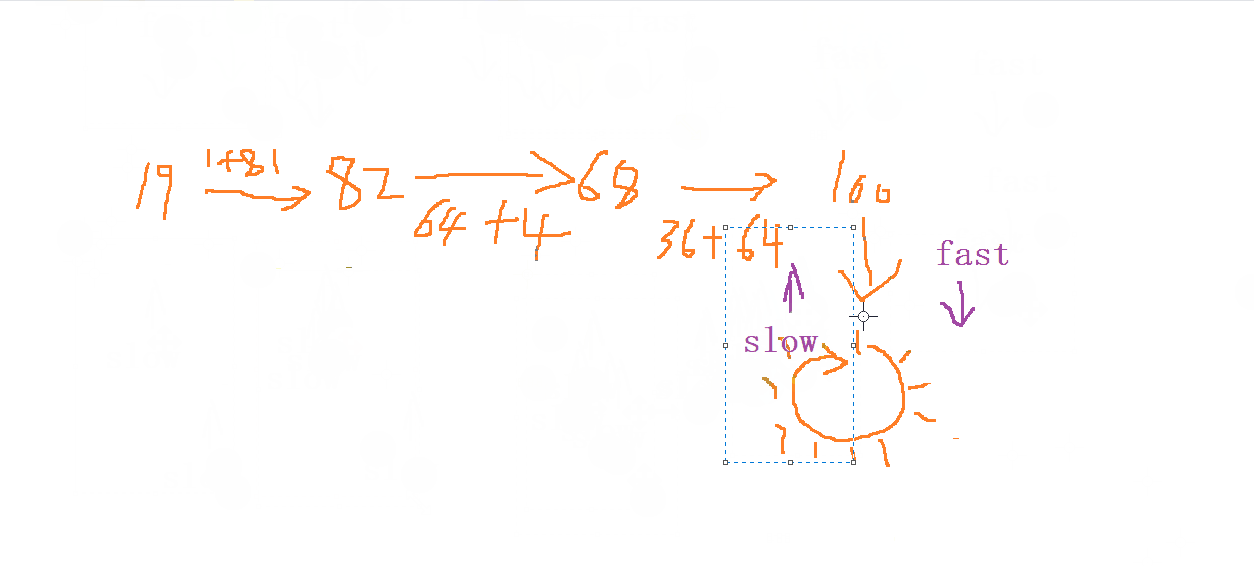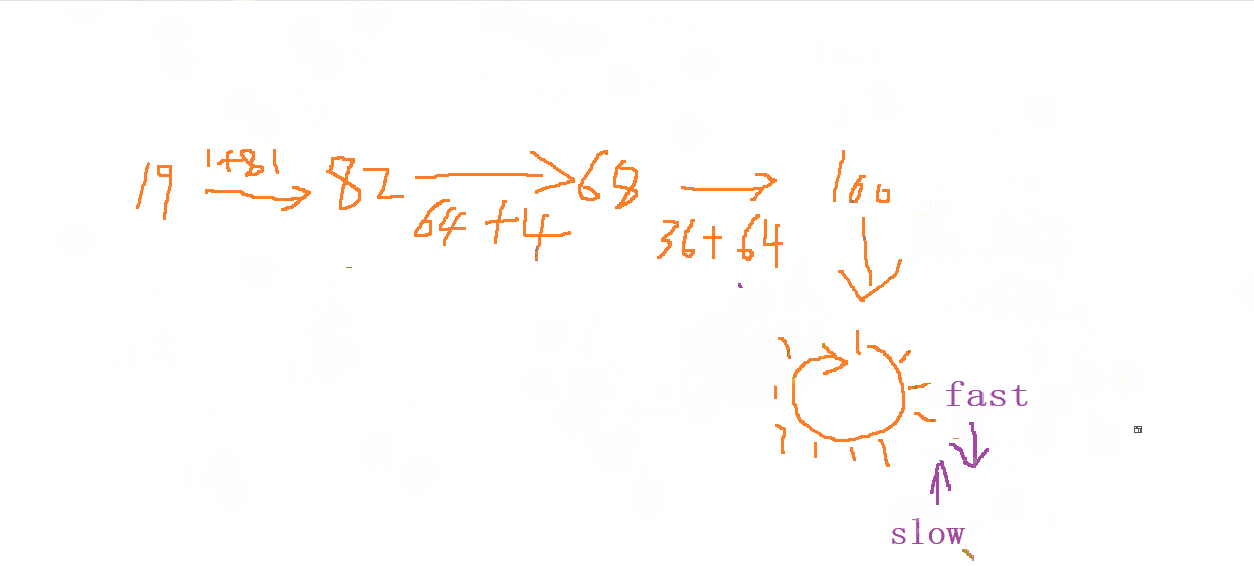
請添加圖片描述

<3>. 編寫代碼

class Solution {public boolean isHappy(int n) {int slow=n;int fast=happyFunc(n);// 一定會成環的while(slow != fast) {slow = happyFunc(slow);fast = happyFunc(happyFunc(fast));}// 最終相遇時只要為 1 就為快樂數if(slow==1) {return true;}return false;}private int happyFunc(int n) {int sum=0;while(n != 0) {int t = n % 10;sum += (t*t);n /= 10; }return sum;}}

在這里插入圖片描述

魚式瘋言

先說幾點體會吧

當我們碰到一個成環或者循環的一種結構時, 快慢指針的思路是很有必要去嘗試的

本題的特點最終是會成為一個 特定的值 , 我們只需要循環判斷即可

本題細節 ：

int slow=n;int fast=happyFunc(n);

初始化的時候

不可以讓 fast 和 slow 同時為 n ，否則就進入不了循環 .

3. 查找總價值為目標值的兩個商品

179. 查找總價值為目標值的兩個商品題目鏈接

<1>. 題目描述

在這里插入圖片描述

輸入一個遞增排序的數組和一個數字s ，在數組中查找兩個數，使得它們的和正好是s 。如果有多
對數字的和等于s ，則輸出 任意一對 即可。

示例 1：
輸入： nums = [2,7,11,15], target = 9
輸出： [2,7] 或者 [7,2]

題目含義 就是找兩個和為 s 的數字

<2>. 講解算法思想

題目分析

如果我們要求兩個數的 和 ，只需要先 固定 一個數，然后再尋找其他數判斷即可尋找到

暴力枚舉

兩層 for 循環列出所有兩個數字的組合，判斷是否等于目標值。

雙指針 的思路

當我們看到一個有序數組的時候，我們頭腦中就得建立兩個思路：

一個二分查找算法

一個雙指針算法

而在本題中更適合用我們的雙指針來解決 兩數和 的問題

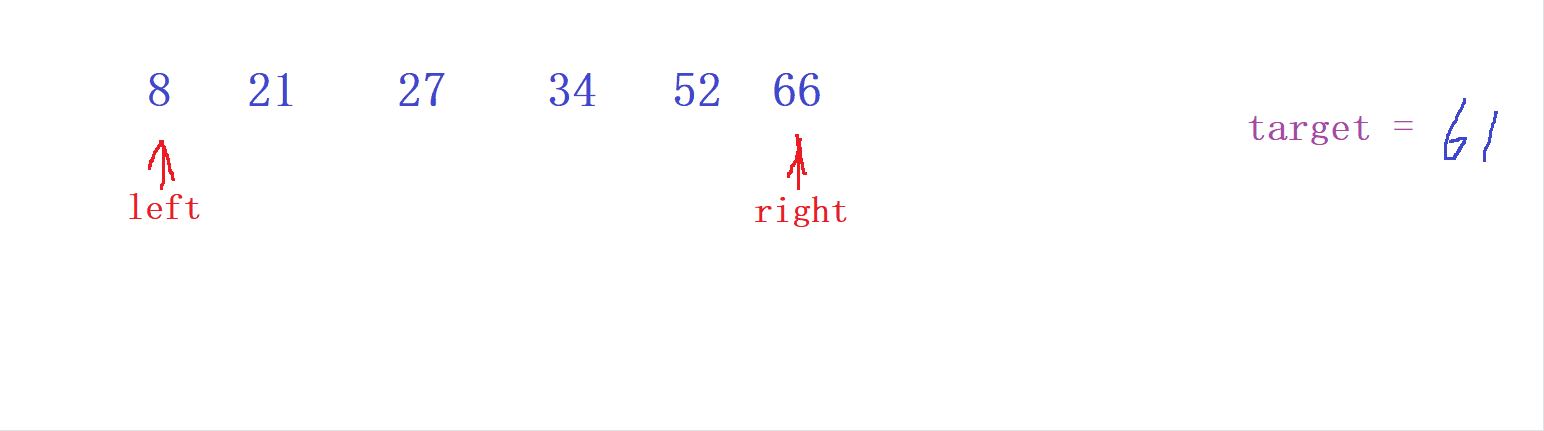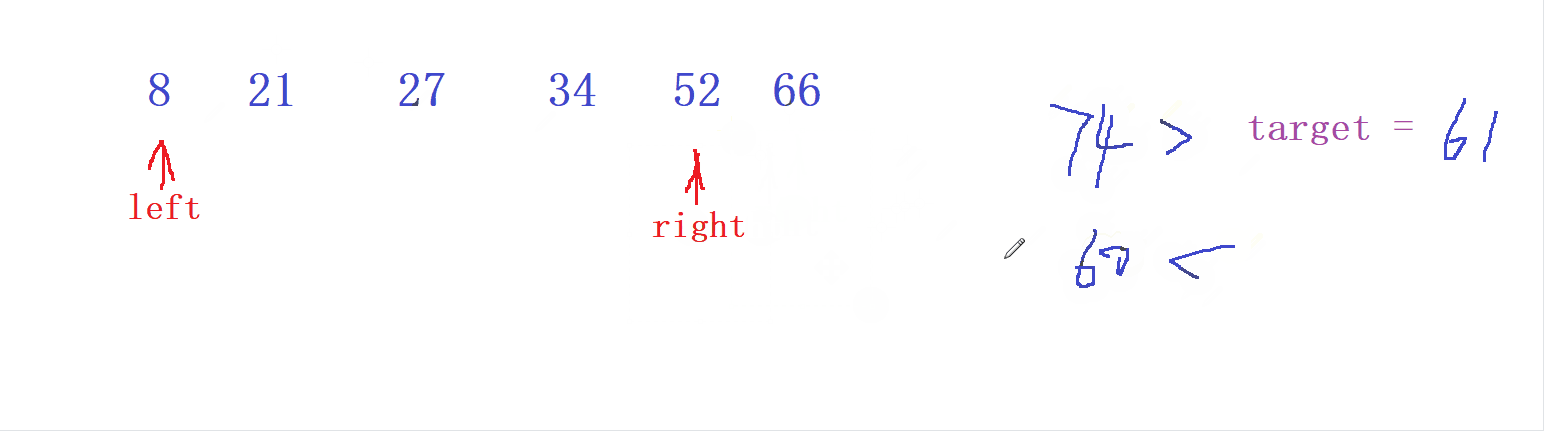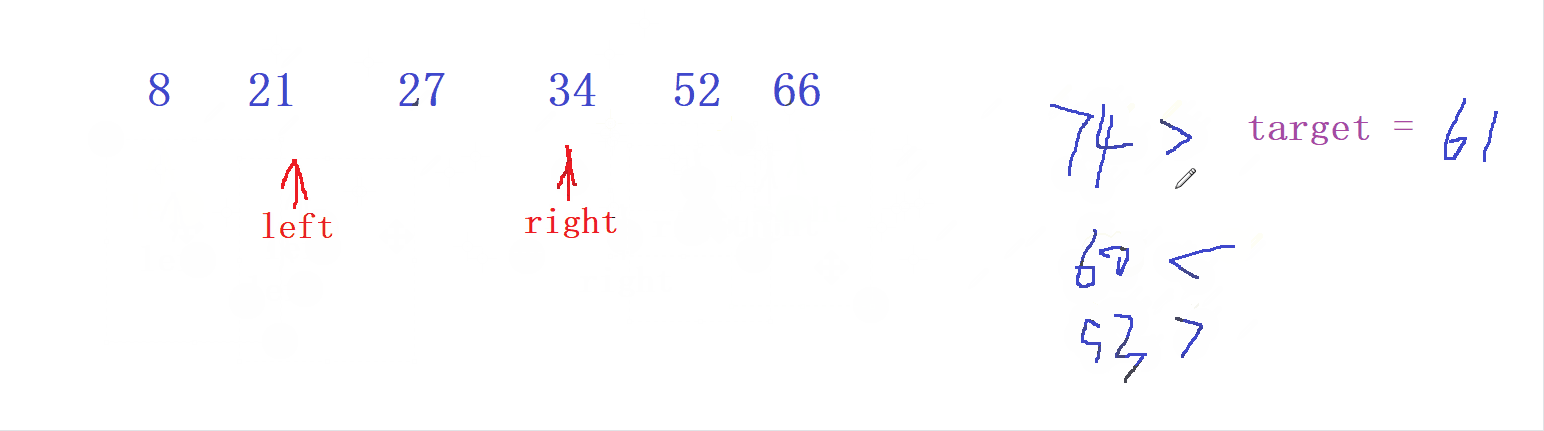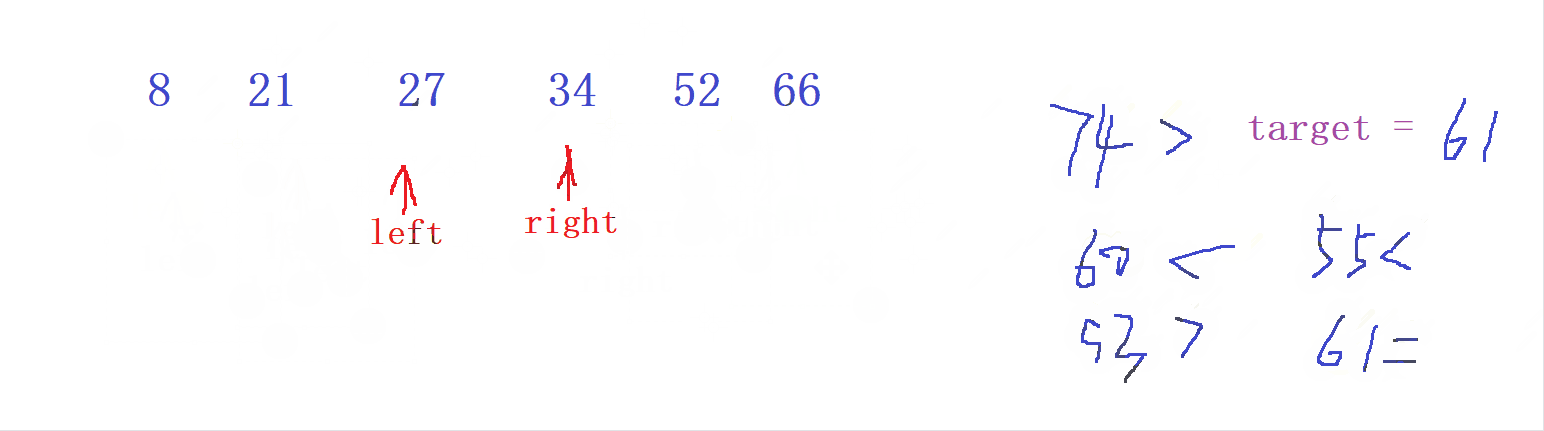
先定義一個指針為 left = 0 ，另一個指針為 right = n-1

當 left 和 right 的數值之和 > target 時 ,我們就讓較大值 right --

當 left 和 right 的數組之和 < target 時，我們就讓較小值 left ++ ;

直到最終相遇或者尋找到目標值 target 為止，

請添加圖片描述

<3>. 編寫代碼

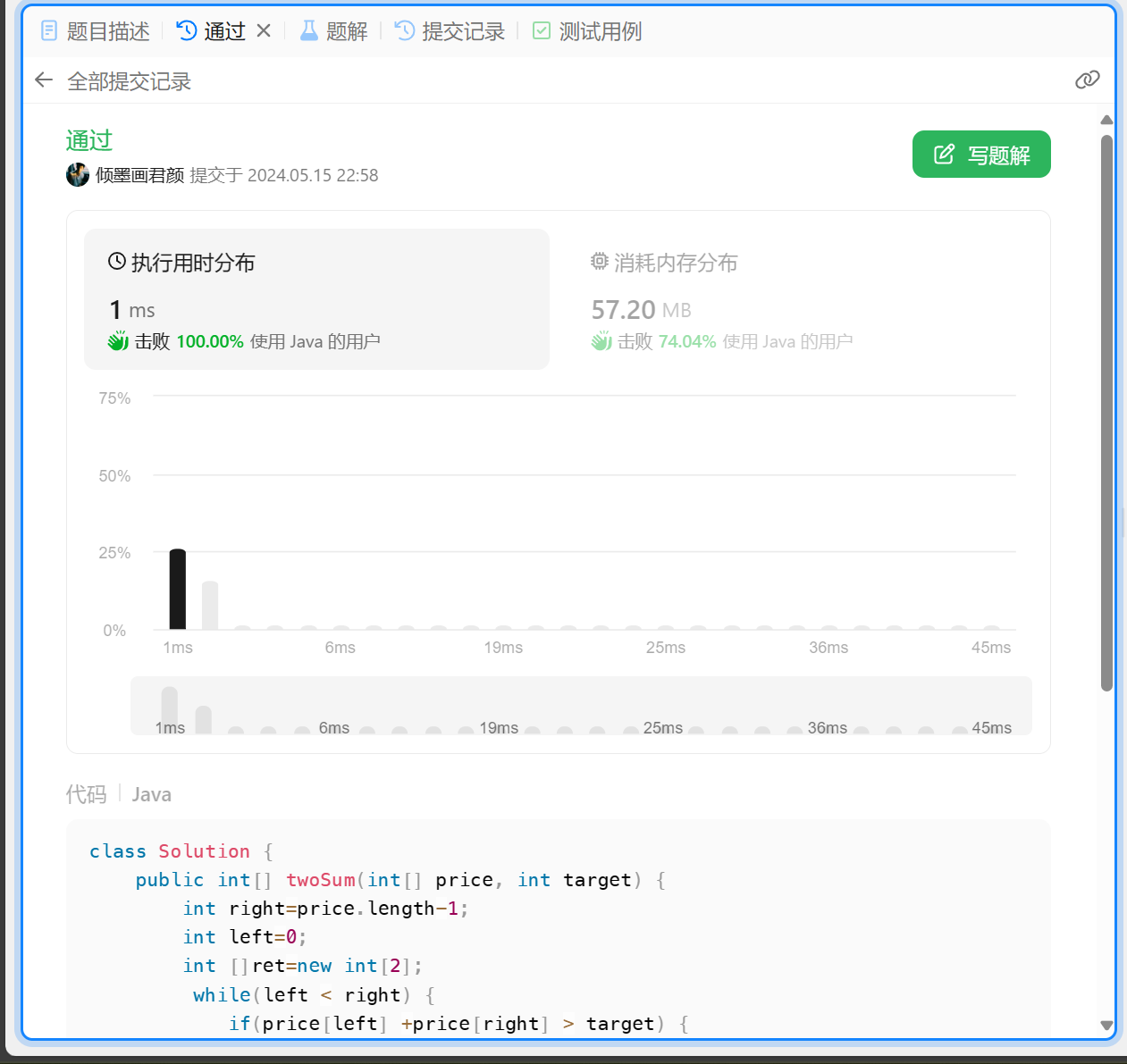
class Solution {public int[] twoSum(int[] price, int target) {int right=price.length-1;int left=0;int []ret=new int[2];while(left < right) {if(price[left] +price[right] > target) {right--;} else if (price[left] +price[right] < target){left++;} else {ret[0]=price[left];ret[1]=price[right];return ret; }}  return ret; }
}

在這里插入圖片描述

魚式瘋言

記住一點

有序就要想到用二分查找算法或者雙指針算法

4 有效三角形個數

611.有效三角形個數題目鏈接

<1>. 題目描述

在這里插入圖片描述

給定一個包含非負整數的數組 nums ，返回其中可以組成三角形三條邊的三元組個數。

示例 1:

輸入: nums = [2,2,3,4]
輸出: 3
解釋:有效的組合是:
2,3,4 (使用第一個 2)
2,3,4 (使用第二個 2)
2,2,3

示例 2:

輸入: nums = [4,2,3,4]
輸出: 4

題目含義 :

找出所有能滿足組合三角形三條邊的個數（包含相同數字的邊）

<2>. 講解算法思想

題目分析

如果我們要找三條邊，先 固定兩個數 的基礎上

再找另外一個數來判斷是否滿足 三角形 的 三邊條件

算法過程

解法一 ：暴力枚舉

用三個 for= 來查找是否存在該數據

解法二 : 雙指針算法

先將數組排序

根據「解法一」中的優化思想，我們可以固定一個「最長邊」，然后在比這條邊小的有序數組中找
出一個二元組，使這個二元組之和大于這個最長邊。由于數組是有序的，我們可以利用「對撞指
針」來優化。

設最長邊枚舉到 i 位置，區間 [left, right] 是 i 位置**左邊的區間（**也就是比它小的區
間）：

? 如果 nums[left] + nums[right] > nums[i] ：

? 說明 [left, right - 1] 區間上的所有元素均可以與 nums[right] 構成比
nums[i] 大的二元組

? 滿足條件的有 right - left 種

? 此時 right 位置的元素的所有情況相當于全部考慮完畢， right-- ，進入下一輪判斷

? 如果 nums[left] + nums[right] <= nums[i] ：

? 說明 left 位置的元素是不可能與 [left + 1, right] 位置上的元素構成滿足條件
的二元組

? left 位置的元素可以舍去， left++ 進入下輪循環

請添加圖片描述

<3>. 編寫代碼

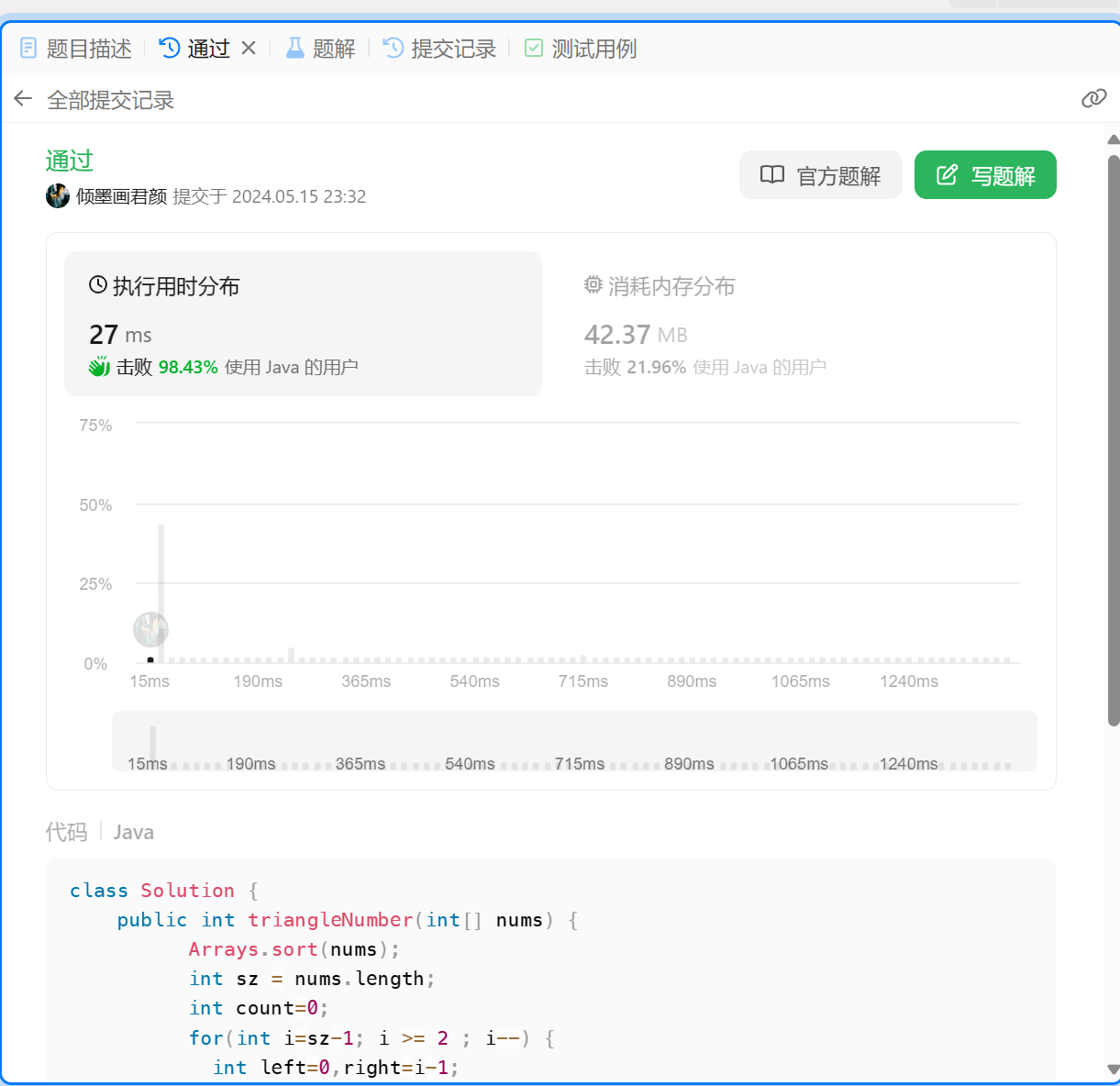
class Solution {public int triangleNumber(int[] nums) {Arrays.sort(nums);int sz = nums.length;int count=0;for(int i=sz-1; i >= 2 ; i--) {int left=0,right=i-1;while(left < right) {if(nums[left] + nums[right] > nums[i]) {count += (right-left);right--;} else {left++;}}}return count;  }
}