前言

組合側重于描述由一些基點生成新的點，強調的是不同點的權重和幾何位置。
集合側重于描述許多個點形成的形狀，強調的是完整性和連通性。

組合

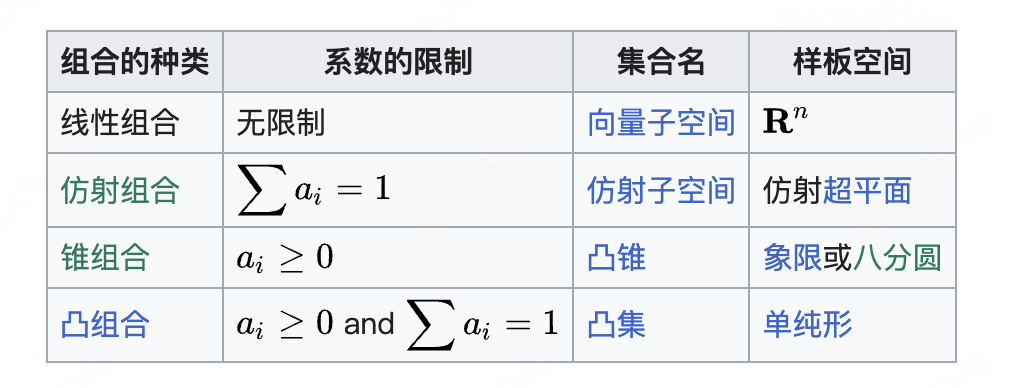
線性組合 (linear combination)

$S$是一向量空間$V$的子集合，如果存在有限多個向量屬于$S$，和對應的標量$a_1,a_2,...,a_n\in F$，使得：
$$v=\sum _{i=1}^n{a}_i{v}_i=a_1{v}_1+a_2{v}_2+...+a_n{v}_n$$
我們稱$v$是$(v_1,...,v_n)$的線性組合。

在二維空間里，如果對${\alpha }_n$沒有任何限制的話，$a_1{v}_1+a_2{v}_2+...+a_n{v}_n$可以擴散出整個空間。

仿射組合 (affine combination)

在上面線性組合的定義中，如果
$$\sum _{i=1}^n{a}_i=1$$
我們則稱$v$是$(v_1,...,v_n)$的仿射組合。

在二維空間里，仿射組合可以看作一條經過兩個點的直線（兩端可以無限延伸）。

錐組合 (conic combination)

在上面線性組合的定義中，如果
$$a_i\ge 1$$
我們則稱$v$是$(v_1,...,v_n)$的錐組合。像個冰淇淋🍦一樣。

在二維空間里，可以想象是從一條原點出發的射線區域。

凸組合 (convex combination)

在上面線性組合的定義中，如果
$$a_i\ge 1，且\sum _{i=1}^n{a}_i=1$$
我們則稱$v$是$(v_1,...,v_n)$的凸組合，可以看到凸組合的要求是最嚴格的，相當于是錐組合和仿射組合的交集。

在二維空間里，凸組合可以看作一條經過兩個點的線段。

集合

仿射集合

仿射集合里任意兩點的連線仍然在集合里。

凸集合

凸集合里任意兩點的線段都在集合里。比如一個圓形，就是一個凸集合，但它不是一個放射集合。

練習：哪個圖形是凸的，哪個是仿射的？

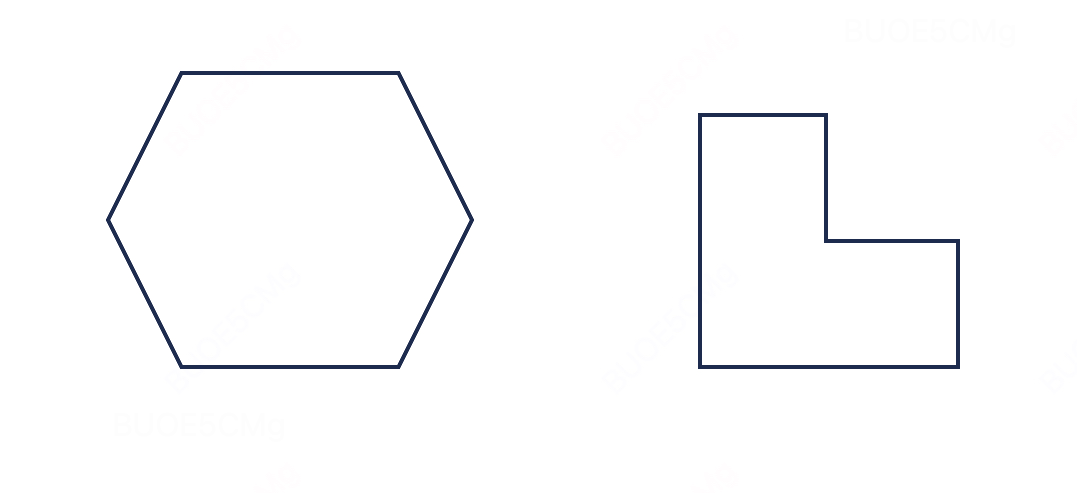
下面兩幅圖，哪個是凸的，哪個是仿射的？

• 左圖：凸的，但不是仿射的；
• 右圖：不是凸的，也不是仿射的。
  

參考資料

1. 線性規劃 方述誠
2. 線性組合