DP

動態規劃（英語：Dynamic programming，簡稱 DP）是一種在數學、管理科學、計算機科學、經濟學和生物信息學中使用的，通過把原問題分解為相對簡單的子問題的方式求解復雜問題的方法。

動態規劃常常適用于有重疊子問題和最優子結構性質的問題，并且記錄所有子問題的結果，因此動態規劃方法所耗時間往往遠少于樸素解法。

動態規劃有自底向上和自頂向下兩種解決問題的方式。自頂向下即記憶化遞歸，自底向上就是遞推。

使用動態規劃解決的問題有個明顯的特點，一旦一個子問題的求解得到結果，以后的計算過程就不會修改它，這樣的特點叫做無后效性，求解問題的過程形成了一張有向無環圖。動態規劃只解決每個子問題一次，具有天然剪枝的功能，從而減少計算量。

樹

樹是所有節點的集合，最上面的節點是根，最下面的節點是葉。樹的集合就是森林。樹是遞歸定義的，因為每一個節點都可以拆成根+子樹。子樹又可以拆分，一直拆分，也就是遞歸了。

葉的度

該節點下面直接相連的節點個數

樹的度

整個樹中最大的葉的度

節點的層次

從根開始定義起，根為第1層，根的子節點為第2層，以此類推；如果一個樹的根為0層的話，那空樹只能用-1來表示了。這就是復數了。為了方便表示，讓空樹等于0，根為1層比較好。本片所用的理論就是根為1層。

節點的祖先

從根到該節點所經分支上的所有節點

節點的子孫

以某節點為根的子樹中任一節點都稱為該節點的子孫

雙親節點或父節點

若一個節點含有子節點，則這個節點稱為其子節點的父節點； 如上圖：A是B
的父節點

樹的表示

樹結構相對線性表就比較復雜了，要存儲表示起來就比較麻煩了，實際中樹有很多種表示方式，
如：雙親表示法，孩子表示法、孩子兄弟表示法等等。我們這里就簡單的了解其中最常用的孩子
兄弟表示法。

孩子兄弟表示法

typedef int DataType;
struct Node
{struct Node* _firstChild1;    // 第一個孩子結點struct Node* _pNextBrother;   // 指向其下一個兄弟結點DataType _data;               // 結點中的數據域
};

這個樹的結構叫：左孩子，右兄弟。

什么意思呢，就是如果這個節點有子節點，也就是該節點的孩子，就讓這個節點的左孩子指針保存孩子的地址，如果該節點沒用孩子，就指向空，如果該節點的父節點除了該節點還有其他的子節點，就讓該節點的右兄弟指向兄弟節點。這里的兄弟只算親兄弟，也就是同一個父親的兄弟。

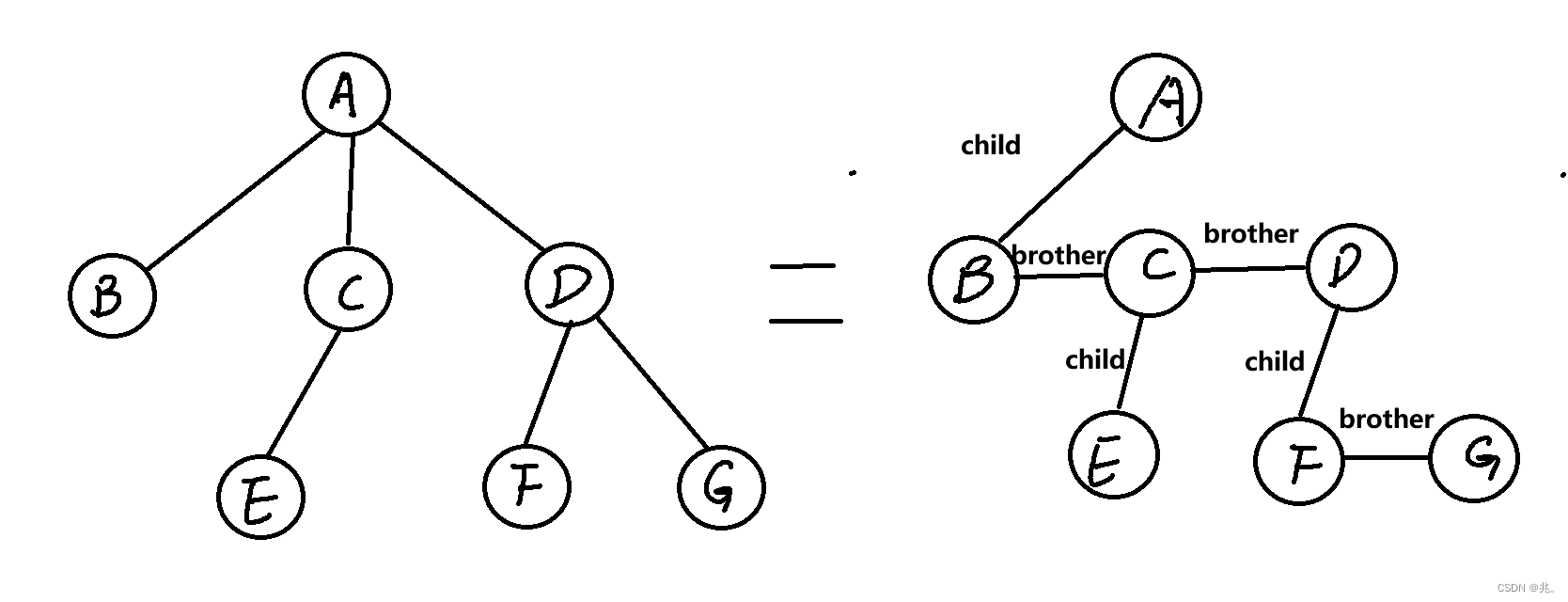
對于一個正常的樹狀結構來說，需要進一步的轉換才能用左孩子右兄弟的方法來表示。就像左邊這個樹，BCD是A的孩子，A只需要指向他最左邊的孩子B就行，然后用B的右兄弟指針連接C，再讓C的右兄弟連接D。發現B沒有孩子，就讓B的左孩子指向空。C的孩子是E，就讓左孩子指向E。E既沒有孩子，也沒有兄弟，左孩子和右兄弟指針都指向空。然后返回上一節點C，再通過C去找D，D有孩子F，D的左孩子就指向F，F還有一個兄弟，就讓F的右兄弟指向G。到這里就都連接完了，其他沒用的指針都指向空。

雙親表示法

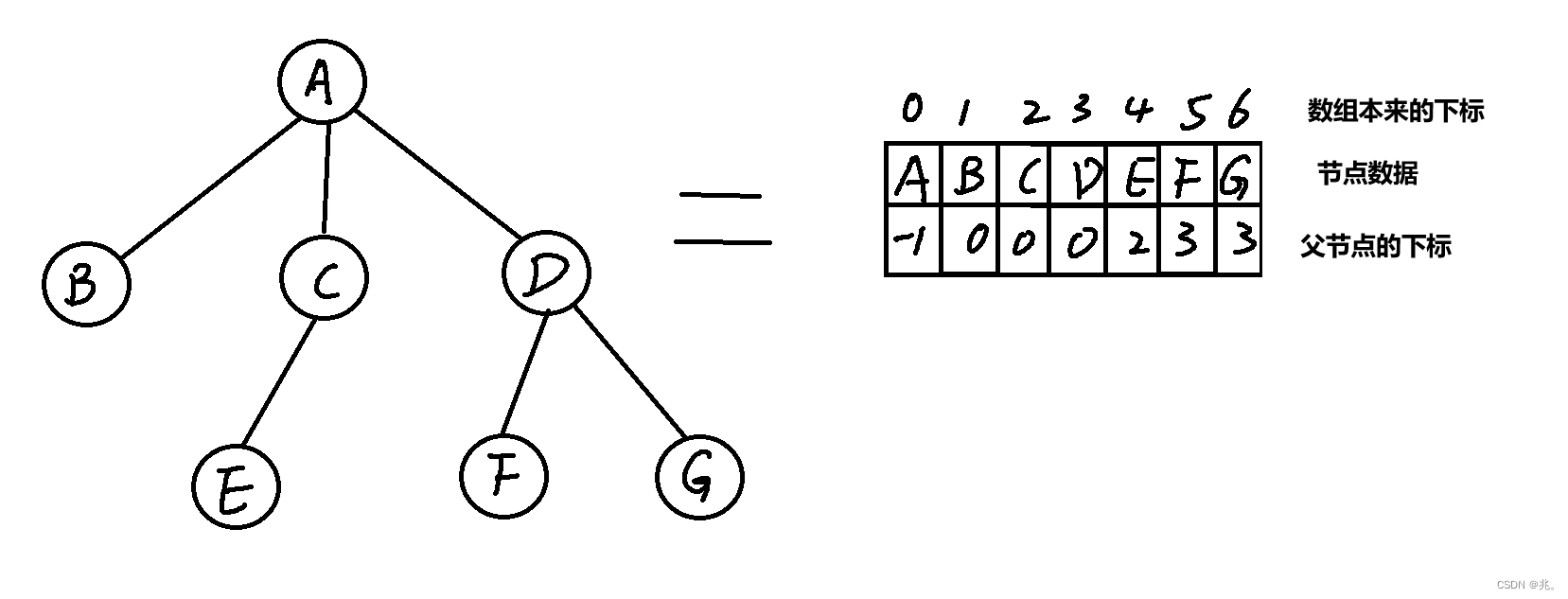
因為一個父親可以有多個孩子，但是一個孩子只能有一個父親，所以可以逆向思考，讓孩子存父親節點。

這里的樹的結構體要全部存在數組中，就是定義一個指針數組，數組的每個元素都是指針，每個指針指向一個樹的節點。

優點是：尋找父節點的題

缺點是：找孩子節點要變量整個數組，也就是整個樹。

樹和非樹

子樹不可相交，每個子樹僅有一個父節點，一顆樹有N個節點，有N-1條邊。不能有孤立的點。比如，5個節點的樹，一定有4條邊。

就是樹不能成環，不能有回路，以后學的圖的可能有回路，等等

樹的應用

目錄樹，C盤，D盤了，文件夾就是節點，文件可能是節點可能是葉子

---

二叉樹

二叉樹是特殊的樹，就是度為2的樹。每個節點最多兩個孩子，也可以是空節點，那就是葉子

滿二叉樹

就是每個節點都是滿的，除了葉子。根節點為1

結論：一個完全二叉樹的層次為k，那么總的節點個數就是(2^k-1),等比數列求和

每一層的節點個數就是2^k-1 個

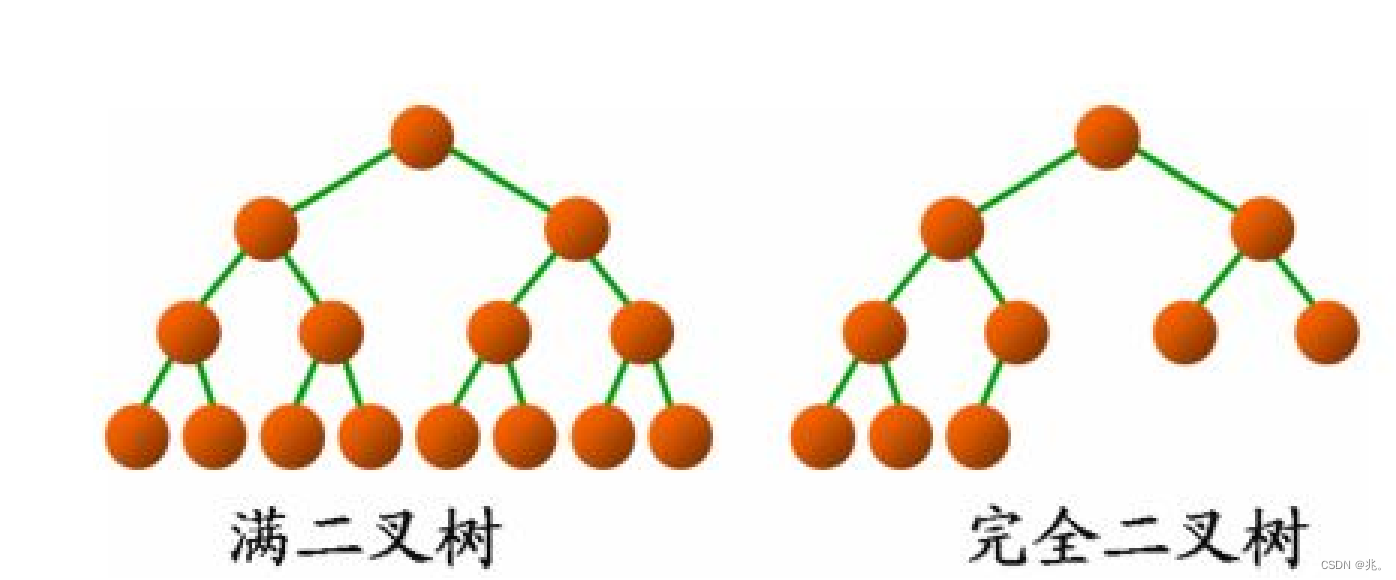
完全二叉樹

完全二叉樹的最底層可以不完整，但是必須從左到右連續。最后一層不滿，但連續。滿二叉樹是特殊的完全二叉樹。

樹–>二叉樹–>完全二叉樹–>滿二叉樹

推論

二叉樹的（葉子節點的個數）是（度為2的節點的個數+1）。葉節點的個數是有倆孩子節點個數的多一個。

如果一個二叉樹有N個節點，高度是h。

• 對于滿二叉樹來說：2*h-1=N；h=log₂(N+1)
• 對于完全二叉樹來說：2*h -1-X=N。（0<=x<=2^h-1-1) ,log₂N <= h <=log₂(N + 1)

例題：

1. 某二叉樹共有 399 個結點，其中有 199 個度為 2 的結點，則該二叉樹中的葉子結點數為（ B ）
A 不存在這樣的二叉樹
B 200
C 198
D 199
2.在具有 2n 個結點的完全二叉樹中，葉子結點個數為（ A ）
A n
B n+1
C n-1
D n/2
3.一棵完全二叉樹的節點數位為531個，那么這棵樹的高度為（ B ）
A 11
B 10
C 8
D 12

二叉樹的存儲

以數組的方式

從根節點開始在數組下標為0的地方，然后從左到右依次填入數組，對于完全二叉樹來說。

• 若一個父節點的下標是i，那么孩子的下標分別是：2i+1和2i+2。i=4.2i+1=9,2i+2=10。
• 若一個子節點的下標是i，那么父節點下標是：（i-1)/2。(6-1)/2=5/2=2. (5-1)/2=4/2=2。

以鏈表的方式

鏈表的方式大概有兩種：二叉鏈表，三叉鏈表。

二叉鏈表，就是有兩個子節點指針的鏈表，三叉鏈表就是有兩個子節點child指針，還有一個父節點parent指針。二叉鏈表，應用的比較多。三叉樹一般應用在平衡樹，紅黑樹等等。

// 二叉鏈
struct BinaryTreeNode
{struct BinTreeNode* pLeft;   // 指向當前節點左孩子struct BinTreeNode* pRight; // 指向當前節點右孩子BTDataType _data; // 當前節點的值
}
// 三叉鏈
struct BinaryTreeNode
{struct BinTreeNode* pParent; // 指向當前節點的父親struct BinTreeNode* pLeft;   // 指向當前節點左孩子struct BinTreeNode* pRight; // 指向當前節點右孩子BTDataType _data; // 當前節點的值
}；

堆(Heap)

堆就是完全二叉樹，用數組來儲存。

堆的分類

• 大堆（大根堆）

每個父節點都大于等于子節點。左右孩子大小不規定。

• 小堆（小根堆）

每個父節點都小于等于子節點。左右孩子大小不規定。

大根堆和小根堆的作用

根（堆頂）是最大值或最小值。應用在堆排序中。

例題：

1.下列關鍵字序列為堆的是:（A)
A 100,60,70,50,32,65
B 60,70,65,50,32,100
C 65,100,70,32,50,60
D 70,65,100,32,50,60
E 32,50,100,70,65,60
F 50,100,70,65,60,32

二叉樹的遍歷

由于二叉樹是一個非線性結構，不同于以往的單鏈表或者數組，只能從頭到尾，或者從尾到頭的遍歷順序。

二叉樹可分為左子樹、右子樹、根三部分。根據三個部分的先后順序劃分，有三種分法：

1. 前序（先根遍歷）：根->左子樹->右子樹
2. 中序（中根遍歷）：左子樹->根->右子樹
3. 后序（后根遍歷）：左子樹->右子樹->根

DFS和BFS

深度優先搜索算法（英語：Depth-First-Search，DFS）是一種用于遍歷或搜索樹或圖的算法。其過程簡要來說是對每一個可能的分支路徑深入到不能再深入為止，而且每個結點只能訪問一次.

因發明「深度優先搜索算法」，約翰 · 霍普克洛夫特與羅伯特 · 塔揚在1986年共同獲得計算機領域的最高獎：圖靈獎。

廣度優先搜索算法（Breadth-First Search，縮寫為 BFS），又稱為寬度優先搜索，是一種圖形搜索算法。簡單的說，BFS 是從根結點開始，沿著樹的寬度遍歷樹的結點。如果所有結點均被訪問，則算法中止。

又因為二叉樹結構的特殊性，有層數之分，根據探索的層數有兩種分法：深度優先遍歷，廣度優先遍歷

其中深度優先遍歷就是：前中后序這三種方式

廣度優先遍歷是層序。所謂的層序就是一層層的挨著訪問。從左到右。

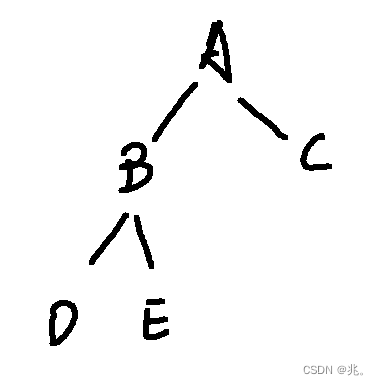
舉個例子：

1. 前序：A->B->D->NULL->NULL->E->NULL->NULL->C->NULL->NULL

   一般方便表示，不會寫NULL，也就是ABDEC.

2. 中序：NULL->D->NULL->B->NULL->E->NULL->A->NULL->C->NULL

3. 后序：NULL->NULL->D->NULL->NULL->E->B->NULL->NULL->C->A

4. 層序：A->B->C->D->E->NULL->NULL->NULL->NULL->NULL->NULL

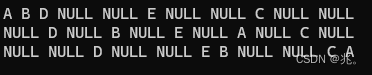
大概是什么意思呢？拿中序來說，拿到這棵樹，第一個節點也就是根，但是不會訪問他的值，因為中序訪問就是先訪問左子樹，對于A這棵樹而言，左子樹是以B為根的子樹，但是這時候不能訪問B的值，因為對于B而言，D才是B的左子樹，對于D而言，左子樹為空，返回NULL（這也就是中序第一個NULL的來源）。然后返回D節點，D是以D為根的子樹的根，D的左子樹已經訪問完了，所以要訪問D，然后訪問D這棵樹的右子樹，右子樹還是空，返回NULL。以D為根的子樹才徹底訪問完畢。D又是B的左子樹，以B為根的子樹的左子樹訪問完，才訪問根B的值。接著是B的右子樹E。以E為根的子樹還要先訪問左子樹。。。。。。。

不難發現，中序是先沿著左子樹這條路，一直找到了D的左子樹NULL才停止訪問。然后返回上級D這條岔路口走右子樹。再返回D的上級B岔路口走右子樹。

隨著程序的運行，一開始就先找最深的地方，也就是深度優先遍歷。走到空，無路可走了，才退回來。

所以深度優先適合數組、圖，這種量大的遍歷。

實現深度優先一般用遞歸，棧。

實現廣度優先用隊列。