146.LRU 緩存
. - 力扣(LeetCode)
請你設計并實現一個滿足??LRU (最近最少使用) 緩存?約束的數據結構。
實現?
LRUCache?類:
LRUCache(int capacity)?以?正整數?作為容量?capacity?初始化 LRU 緩存int get(int key)?如果關鍵字?key?存在于緩存中,則返回關鍵字的值,否則返回?-1?。void put(int key, int value)?如果關鍵字?key?已經存在,則變更其數據值?value?;如果不存在,則向緩存中插入該組?key-value?。如果插入操作導致關鍵字數量超過?capacity?,則應該?逐出?最久未使用的關鍵字。函數?
get?和?put?必須以?O(1)?的平均時間復雜度運行。?
思路:雙向鏈表+一個哨兵節點,使用map記錄(key,node)
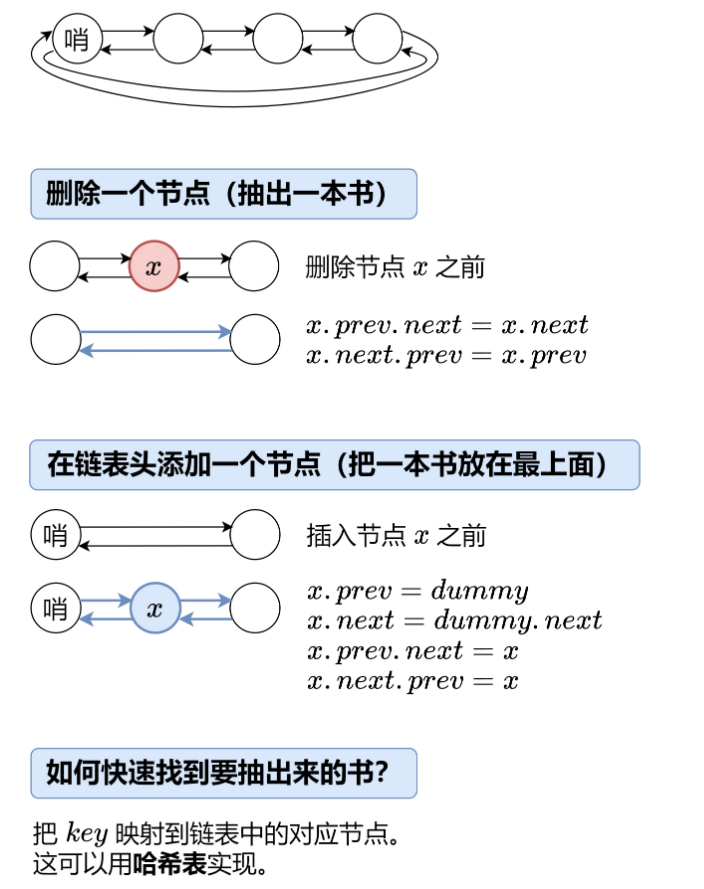
(圖和思路都是偷力扣大佬的)?
實現:
class Node {constructor(key, value) {this.key = keythis.value = valuethis.pre = nullthis.next = null}
}class LRUCache {constructor(capacity) {this.capacity = capacitythis.dummy = new Node()this.dummy.next = this.dummythis.dummy.pre = this.dummy// 哈希表 用來存key和節點nodethis.keyToNodeMap = new Map()}// 刪除x節點delete(x) {x.pre.next = x.nextx.next.pre = x.pre}// 將節點添加在鏈表頭 哨兵節點后addTop(x) {x.pre = this.dummyx.next = this.dummy.nextx.pre.next = xx.next.pre = x}getNode(key) {// 沒有該節點if (!this.keyToNodeMap.has(key)) { return null;}// 有 拿出來放在頭部const node = this.keyToNodeMap.get(key); this.delete(node); this.addTop(node); return node;}get(key) {const node = this.getNode(key)return node?node.value:-1}put(key, value) {let node = this.getNode(key)// 有這個值 拿出來更新if (node) {node.value = value} else {// 新建節點放入node = new Node(key, value)this.keyToNodeMap.set(key, node)this.addTop(node)// 判斷有沒有溢出if (this.keyToNodeMap.size > this.capacity) {const backNode = this.dummy.prethis.keyToNodeMap.delete(backNode.key)this.delete(backNode)}}}
}215.數組中最大的第k個元素
. - 力扣(LeetCode)
給定整數數組?
nums?和整數?k,請返回數組中第?k?個最大的元素。請注意,你需要找的是數組排序后的第?
k?個最大的元素,而不是第?k?個不同的元素。你必須設計并實現時間復雜度為?
O(n)?的算法解決此問題。?
思路:
看的是這位佬的:. - 力扣(LeetCode)
利用大根堆根節點最大的特性,構建大根堆,將根節點與最末尾節點交換,移出這個最大節點,再進行排序。。。
利用的是堆的思想,但實際是用數組來實現的?
順序存儲二叉樹的特點:
第 n 個元素的 左子節點 為 2*n+1
第 n 個元素的 右子節點 為 2*n+2
第 n 個元素的 父節點 為 (n-1)/2
最后一個非葉子節點為 Math.floor(arr.length/2)-1
實現:
var findKthLargest = function (nums, k) {let len = nums.length// 先構建大根堆buildMaxHeap(nums, len)// 循環 將大根堆根節點和最末尾的節點交換// 循環到第k+1個最大就停止 最后返回的nums的根節點就是目標數// 這里for循環要用nums.length,不能用len,因為len是會改變的for (let i = nums.length - 1; i >= nums.length - k + 1; i--) {swap(nums, 0, i) // 將最大節點和最末尾的節點交換// 調整大根堆maxHeapify(nums, 0, --len) // 移到最后的節點不參與調整}return nums[0] // 返回第k個最大的值// 創建大根堆 自下而上構建大根堆function buildMaxHeap(nums, len) {// 最小非葉子節點:Math.floor(arr.length/2)-1for (let i = Math.floor(len / 2) - 1; i >= 0; i--) {maxHeapify(nums, i, len)}}function maxHeapify(nums, i, len) {let left = i * 2 + 1 // i的左子節點let right = i * 2 + 2 // i的右子節點let largest = i // 最大值的節點下標// 和左子節點比較if (left < len && nums[left] > nums[largest]) {largest = left}// 和右子節點比較if (right < len && nums[right] > nums[largest]) {largest = right}if (i !== largest) {swap(nums, i, largest) // 將子節點與父節點交換maxHeapify(nums, largest, len) // 再繼續向下比較}}function swap(nums, a, b) {let temp = nums[a]nums[a] = nums[b]nums[b] = temp}};?今天寫的兩道都有點難,對于我這個白癡來說,所以明天還要再寫一遍!!!




)





Tkinter筆記(九):用【Button()】功能按鈕實現人機交互)
)
)




)

