概念

機器翻譯就是用計算機把一種語言翻譯成另外一種語言的技術

機器翻譯的產生與發展

17 世紀，笛卡爾與萊布尼茨試圖用統一的數字代碼來編寫詞典
1930 機器腦
1933 蘇聯發明家特洛陽斯基用機械方法將一種語言翻譯為另一種語言
1946 ENIAC 誕生
1949 機器翻譯問題被正式提出
1954 第一個 MT 系統出現
1964 遇到障礙，進入低迷期
1970-1976 開始復蘇
1976-1990 繁榮時期
1990-1999 除了雙語平行預料，沒有其他的發展
1999-now 爆發期
2014 以后出現基于深度學習/神經網絡的 MT

機器翻譯的要點

正確的機器翻譯必須要解決語法與語義歧義
不同類型語言的語言形態不一致
有的詞語在不同語言中不能夠互通

詞匯層的翻譯

（1）形態分析：對于原始的句子進行形態分析，對于時態等特殊要素進行標記
（2）詞匯翻譯
（3）詞匯重排序
（4）形態變換

語法層的翻譯

語法層的翻譯就是將一種語言的語法樹映射到另一語言的語法樹
e.g.英語 ->日語
$VP\to VNPchangetoVP\to NPV$
$PP\to PNPchangetoNP\to NPP$
三個階段：句法分析，轉換句法樹，用目標語法樹生成句子

語義層的翻譯

基本翻譯方法

直接轉換法
基于規則的翻譯方法
基于中間語言的翻譯方法
基于語料庫的翻譯方法

直接轉換法

從源語言的表層出發，直接只換成目標語言譯文，必要時進行簡單詞序調整

基于規則的翻譯方法

把翻譯這一過程與語法分開，用規則描述語法
翻譯過程：
（1）對源語言句子進行詞法分析
（2）對源語言句子進行句法/語義分析
（3）結構轉換
（4）譯文句法結構生成
（5）源語言詞匯到譯文詞匯的轉換
（6）譯文詞法選擇與生成
獨立分析-獨立生成-相關轉換
優缺點：可以較好地保持原文的結構，但是規則一般由人工編寫，工作量大，對非規范語言無法處理

基于中間語言的翻譯方法

源語言解析-比較準確的中間語言-目標語言生成器

基于語料庫的翻譯方法

基于事例的翻譯方法

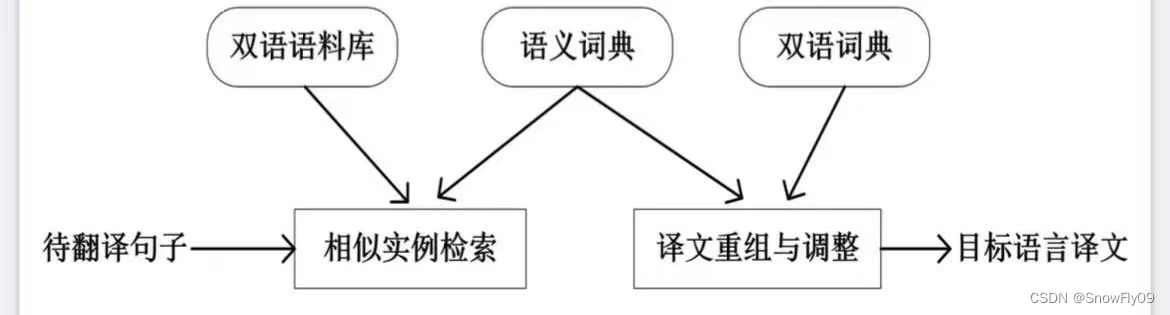
統計機器翻譯

獲取大量各國語言翻譯成英語的文本，然后進行句子對齊
翻譯目標：準確度（faithfulness），結構正確/可讀性強（fluency）
$T=\arg \underset{T\in Target}{\max }faithfulness(T,S)\times fluency(T)$

噪聲信道模型

依然與之前語言模型中的貝葉斯類似
將源語言句子$f=f_1{f}_2...$翻譯到目標語言$e=e_1{e}_2$，使 P（e｜f）最大化
$\hat{e}=\arg \underset{e\in English}{\max }P(e|f)=\arg \underset{e\in English}{\max }P(f|e)P(e)$
此外還需要 decoder 來進行解碼

語言模型 p（e）

可以采用 n-gram 或者 PCFG 計算

翻譯模型 p（f｜e）

對于 IBM Model 1:
（1）選擇長度為 m 的句子 f,英文句子長度為 l
（2）選擇一到多的對齊方式：A = a1a2…an
（3）對于 f 中的單詞 fj，由 e 中相應的對齊詞 $e_{aj}$生成
red：對齊：一種對齊定義了每個外文詞可以由哪個（些）英文詞翻譯過來
目標式可以表示為：$p(f|e,m)=\sum _{a\in A}p(f,a|e,m)$
由鏈式法則可得：$p(f,a|e,m)=p(a|e,m)p(f|a,e,m)$
對于 p（a｜e，m），IBM Model 1 假設所有的對齊方式具有相同的概率：$p(a|e,m)=\frac{1}{(l+1{)}^m}$
對于 p（f｜a，e，m），$p(f|a,e,m)=\prod _{j=1}^{m}t(f_j|e_{aj})$

t(f|e)表示英文詞 eaj 翻譯成外文詞 fj 的概率
故：$p(f|e,m)=\sum p(f,a|e,m)=\sum _{a\in A}\frac{1}{(l+1{)}^m}\prod _{j=1}^{m}t(f_j|e_{aj})$
根據以上計算式，也可以計算某種對齊方式的概率：
$a^{?}\arg {\max }_{a}p(a|f,e,m)=\arg {\max }_a\frac{p(f,a|e,m)}{p(f|e,m)}$

IBM Model 2:
對于 model 2，引入了對齊時的扭曲系數
q（i｜j，l，m）給定 e 和 f 對齊的時候，第 j 個目標語言詞匯和第 i 個英文單詞對齊的概率
$p(a|e,m)=\prod _{j=1}^{m}q(a_j|j,l,m)$
則$p(f,a|e,m)=\prod _{j=1}^{m}q(a_j|j,l,m)t(f_j|e_{aj})$

IBM model 2 最優對齊：

t 與 q 的計算

已有數據：雙語（句子）對齊資料（包含/不包含詞對齊信息）
$e^{(k)},f^{(k)},a^{(k)}$
采用極大似然估計法：
$t_{ML}(f|e)=\frac{Count(e,f)}{Count(e)},t_{ML}(j|i,l,m)=\frac{Count(j|i,l,m)}{Count(i,l,m)}$

如果不包含詞對齊信息：

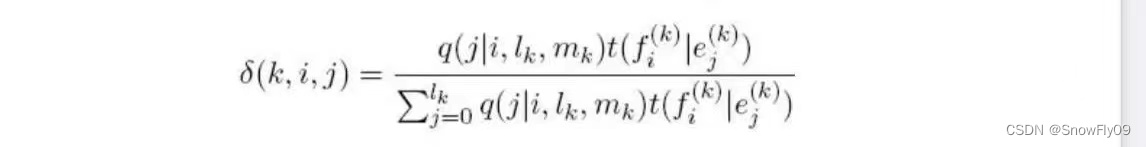
基于短語的翻譯

有時候會出現多個詞對應一個詞的情況，有時候也需要更長的上下文來消除詞的歧義，于是推出了基于短語的翻譯

基本過程

構建短語對齊詞典
基于短語的翻譯模型：
（1）詞組合成短語
（2）短語翻譯
（3）重排序
解碼問題

短語對齊詞典

輸入：句子對齊語料
輸出：短語對齊語料
e.g.他將訪問中國He will visit China
（他將，He will）（訪問中國，visit China）
每個互譯的短語對（f，e）都有一個表示可能性的分值 g（f，e）
$g(f,e)=\log \frac{count(f,e)}{count(e)}$
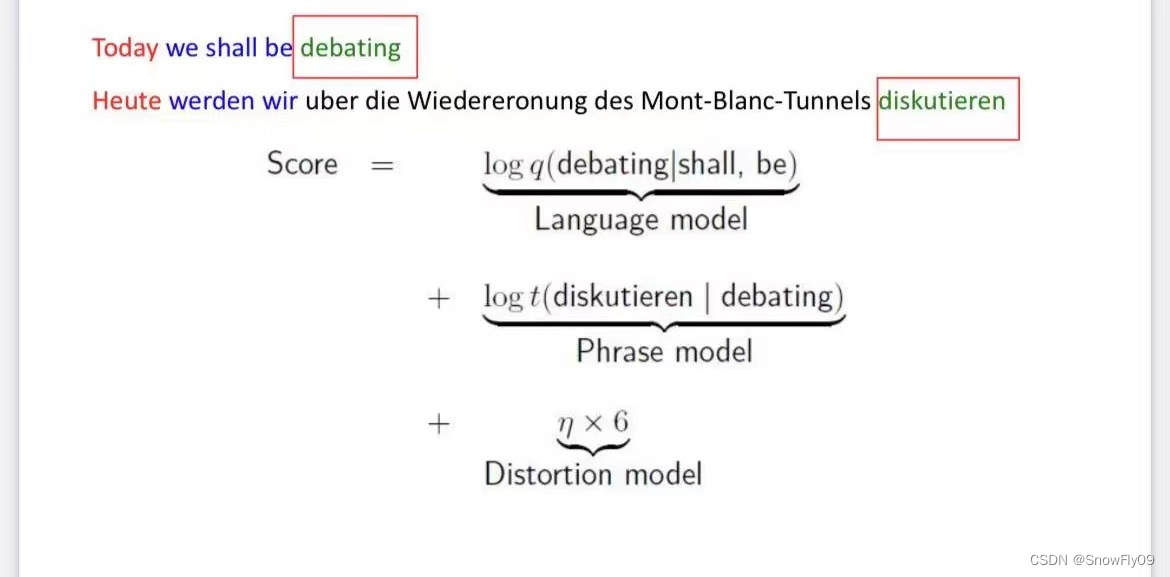
同時使用噪聲信道模型依然可以用來表示最優英語翻譯：
$e_{best}=\arg {\max }_{e}p(f|e)p_{LM}(e)$

語言模型

一般采用 3-gram：q（w｜u，v）

排序模型

可以簡化為基于距離的排序：$\eta \times |star{t}_i?en{d}_{i?1}?1|$
其中 $\eta$為扭曲參數，通常為負值

幾個概念

p（s，t，e）：源句子中 xs 到 xt 的詞串可以被翻譯為目標語言的詞串 e
P：所有短語 p 的集合
y：類似 P，導出，表示一個由有限個短語構成的短語串
e（y）：表示由導出 y 確定的翻譯

解碼問題

求解最優翻譯是一個 NP-complete 問題
可能的方案：基于啟發式搜索解碼算法
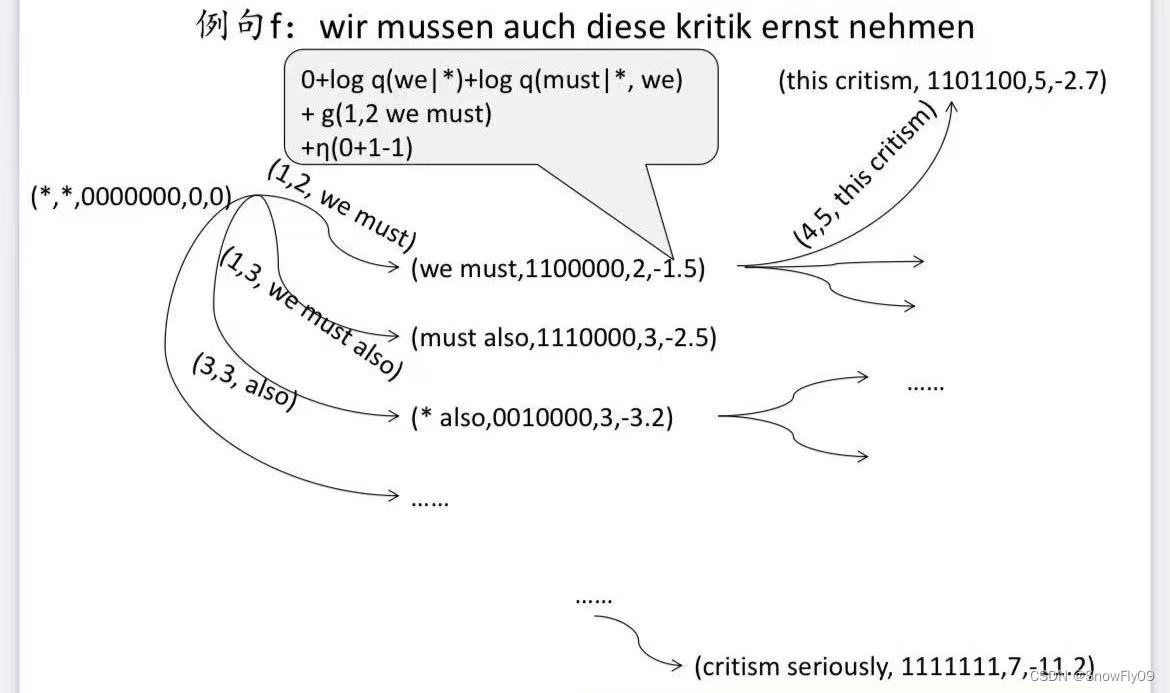
狀態 q：五元組（e1，e2，b，r，alpha）
e1，e2 表示待翻譯短語對應翻譯中最后兩個英文詞
b 為二進制串 ，1 為已經翻譯，0 為未翻譯
r 表示當前待翻譯短語的最后一個詞在句子中的位置
alpha 表示該狀態的得分
起始 $q_0=(/,/,0^n,0,0)$

next(q,p) 表示 q 經過短語 p 觸發，轉移到下一個狀態
eq（q，q‘）用來驗證兩個狀態是否相等，只比較前四項值

beam(Q)