深入淺出遞歸算法

文章目錄

遞歸思想
遞歸的題目
- 1.漢諾塔問題
- - 問題分析
  - 代碼展示
- 2.合并兩個有序鏈表
- - 問題分析
  - 代碼展示
- 3.反轉鏈表
- - 問題分析
  - 代碼展示
- 4.兩兩交換鏈表中的節點
- - 問題分析
  - 代碼展示
總結

遞歸思想

遞歸就是將一個很大的問題拆分成子問題，然后再將子問題繼續拆分，拆分成更小的子問題，最后直到不能拆分為止。
遞歸一共分為三個步驟，首先，我們要將一個問題拆為一些子問題，然后去看這些子問題是否有相同的方法可以繼續拆分，所以遞歸的關鍵就是一個大問題是否能轉換成相同類型的子問題，然后子問題是否又能繼續轉換成相同類型的子問題，注意這里我們就需要搞定我們這個遞歸的函數傳遞的參數具體需要什么，也就是（函數頭），當我們確立了子問題之后，我們就需要進行函數體的書寫了，書寫函數體主要圍繞單個子問題進行，因為，我們的一個大的問題都可以拆分為一個個的小的子問題，所以這些子問題都可以通過一個方法來處理，所以只需要對一個子問題進行書寫函數體就行了，最后，我們需要防止無限遞歸，也就是遞歸的終止條件，向上歸的過程。

總結：遞歸的方法

找到類型相同的子問題
對某個子問題進行函數體方法的書寫
遞歸的出口----終止條件的判斷

遞歸的題目

1.漢諾塔問題

問題分析

輸入和輸入：

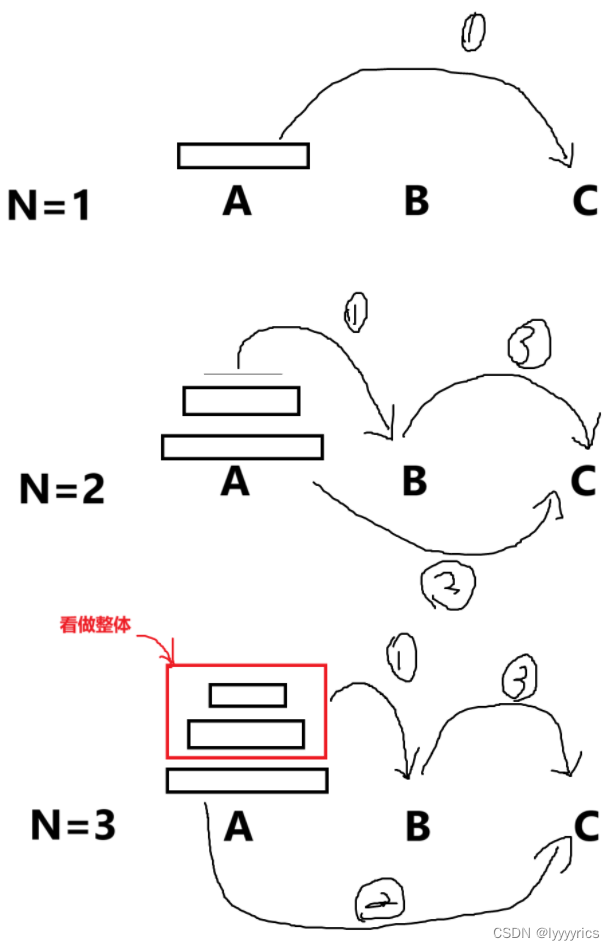
在這里插入圖片描述

首先我們來分析：
1.找到子問題

可以看到子問題很容易就出來了，我們不管有多少個盤子，我們都可以將上面的n-1個盤子看成一個整體，然后將上面n-1個盤子借助C移到B柱上，然后將最下面的盤子移到C上，然后再對上面n-1個盤子實行相同的方法，對上面n-1個盤子上的n-2個盤子用剛剛一樣的方法。

這里子問題找到了，我們就可以確定我們的函數頭和傳遞的參數了，對于上面的圖我們傳遞的函數頭就可以用下面類似方式寫出：dfs(A,B,C,n).
2.用單個子問題尋找函數體
單個子問題是：
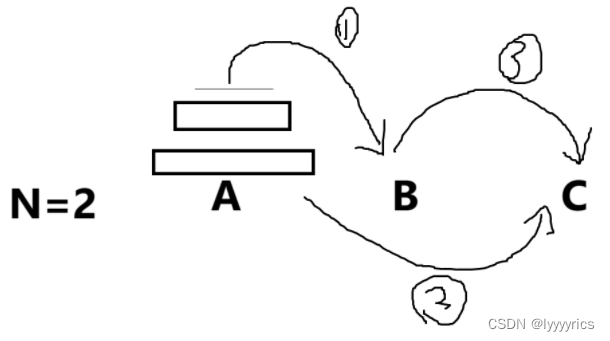
在這里插入圖片描述
首先第一步是：dfs(A,C,B,n-1)

這句代碼的意思是將A柱上n-1個盤子從A移到B上，借助C

第二部是：A.back()->C（偽代碼）

將A上最后一個盤子移到C，當我進行了第一步遞歸之后，只剩下最后一個盤子了，所以，我需要將最后一個盤子移到C上

第三部：dfs(B,A,C,n-1)

將B柱上剩下的盤子移到C上，注意中間的過程我們不需要管，他會不斷拆分，我們只需要找到同一的方法即可

3.遞歸出口
對于遞歸的出口，我們可以看上面的子問題，當我們只有一個盤子的時候我們就直降將這個盤子移到C柱上了，所以這里的最后的遞歸出口就是當只有一個盤子的時候。

代碼展示

class Solution {
public:void dfs(vector<int>& x,vector<int>&y,vector<int>&z,int n){if(n==1)//當只有一個盤子的時候移到z柱上{//移到z柱上z.push_back(x.back());//將x柱上的值刪除x.pop_back();return;}//將x柱上的整體的n-1個盤子整體移到y柱上dfs(x,z,y,n-1);//然后將x柱上剩下的一個盤子移動到z柱上z.push_back(x.back());x.pop_back();//最后將y柱上的剩下的盤子移動到z柱上即可，借助x柱，注意：y柱上有n-1個盤子dfs(y,x,z,n-1);}void hanota(vector<int>& a, vector<int>& b, vector<int>& c){dfs(a,b,c,a.size());}
};

2.合并兩個有序鏈表

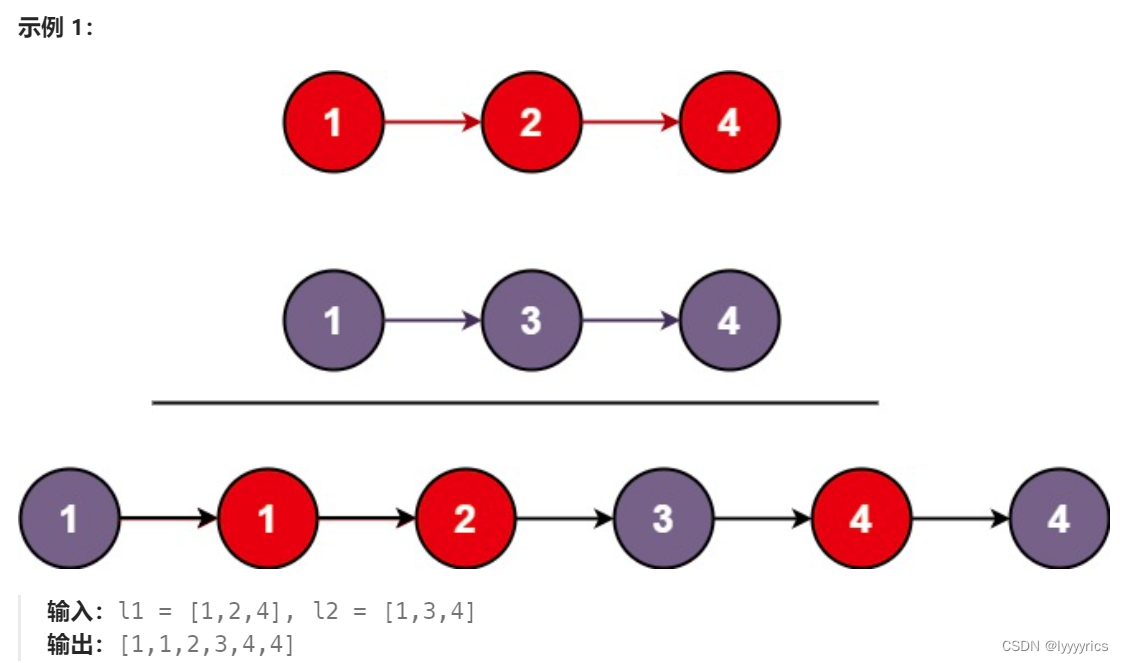
樣例輸入和輸出：

問題分析

1.尋找子問題
這里其實我們可以選一個小的作為頭，選好這個頭之后將這個頭去指向這個函數頭，這個函數頭就是去給我們合并的函數。
確定函數頭：dfs(l1,l2)
2.根據單個子問題找到函數體

這里我們可以通過子問題找到函數體：首先函數頭是傳遞兩個鏈表的頭，然后返回的是新的頭結點，所以這里我們只需要取兩個鏈表的中的小的為新的頭，然后去鏈接剩下的兩個鏈表

函數體：min->next=dfs(min->next,other)

這里大致就可以將函數體寫成這樣，小的鏈表的頭指向小的鏈表的剩下的部分和另一個鏈表

3.遞歸出口
遞歸出口：當有一個函數為空時直接返回另一個鏈表，注意：這里其實可以這樣想，當我們鏈接當一個鏈表為空的時候是不是另一個鏈表鏈接上去肯定是有序的，所以這里我們只需要返回另一個部位空的鏈表即可。

代碼展示

class Solution 
{
public:ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {if(list1==nullptr)return list2;if(list2==nullptr)return list1;if(list1->val<=list2->val){list1->next=mergeTwoLists(list1->next,list2);//list1作為頭結點合并list1->next,和list2return list1;}else{list2->next=mergeTwoLists(list1,list2->next);//連接list2->next和list1return list2;}}
};

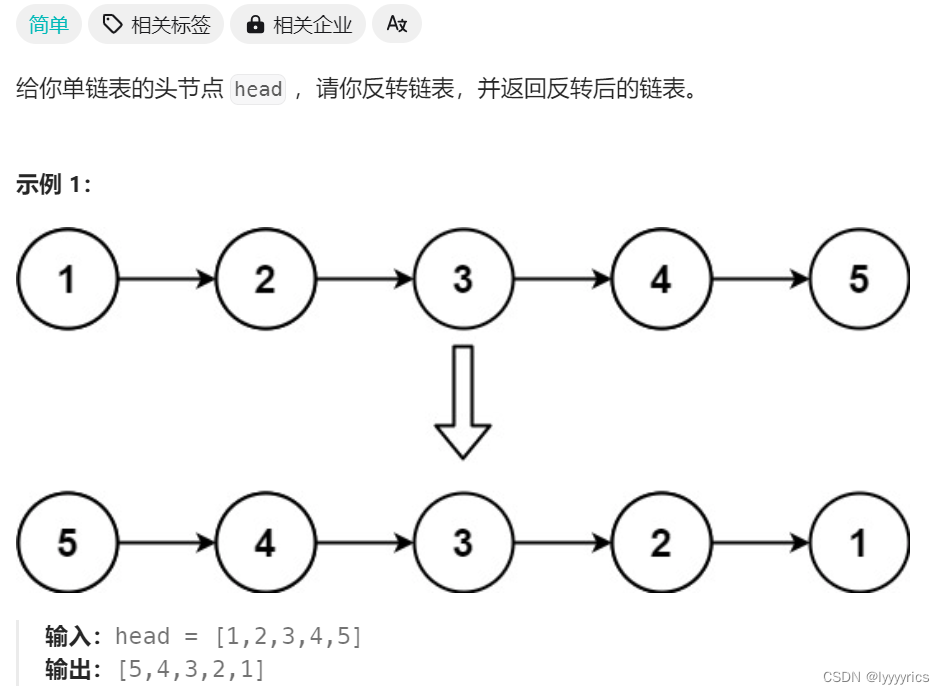
3.反轉鏈表

問題分析

這道題我們其實也可以用遞歸來做，我們要將整個鏈表翻轉其實可以看做將1后面的鏈表翻轉，剩下的鏈表翻轉又可以分解成剩下的鏈表的剩下的部分翻轉，接下來我用一個圖方便理解

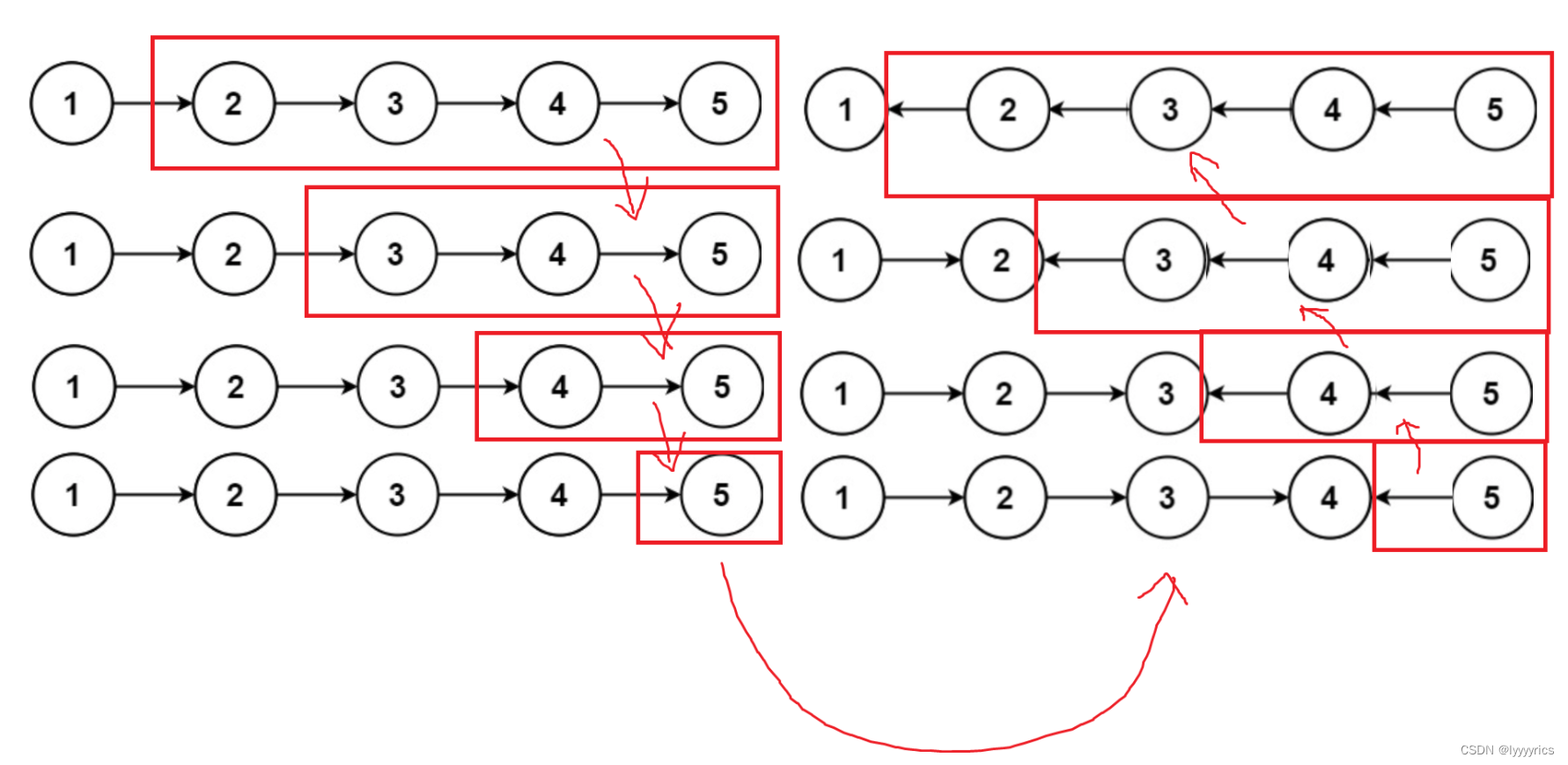
在這里插入圖片描述
大概就是上圖的意思，我們先深度優先遍歷到最后一個節點，然后再向上翻轉注意，這里我沒有志向nullptr，但是我們每次翻轉的時候都要指向nullptr，這是為了遞歸的統一。

函數頭
函數頭：dfs(head)

函數體

函數體：newhead=reverseList(head->next);
我們只需要創一個新的頭來等于剩下的翻轉過的鏈表，注意：這里我們翻轉過的鏈表是抽象的遞歸，具體是怎么完成的計算機會完成，我們只需要給出方法，這里我們已經得到了翻轉鏈表的方法之后，我們就可以直接將就的head與翻轉過的鏈表進行連接即可。

遞歸出口
當當前節點指向的下一個是nullptr的時候或者當當前節點是nullptr的時候就直接返回當前節點。

代碼展示

class Solution 
{
public:ListNode* reverseList(ListNode* head) {//出口if(head==nullptr||head->next==nullptr){return head;}ListNode*newhead=reverseList(head->next);//原本head->next是head的next但是現在要反轉過來//就要把head的next節點指向自己就是head->next->next=head;head->next->next=head;head->next=nullptr;return newhead;}
};

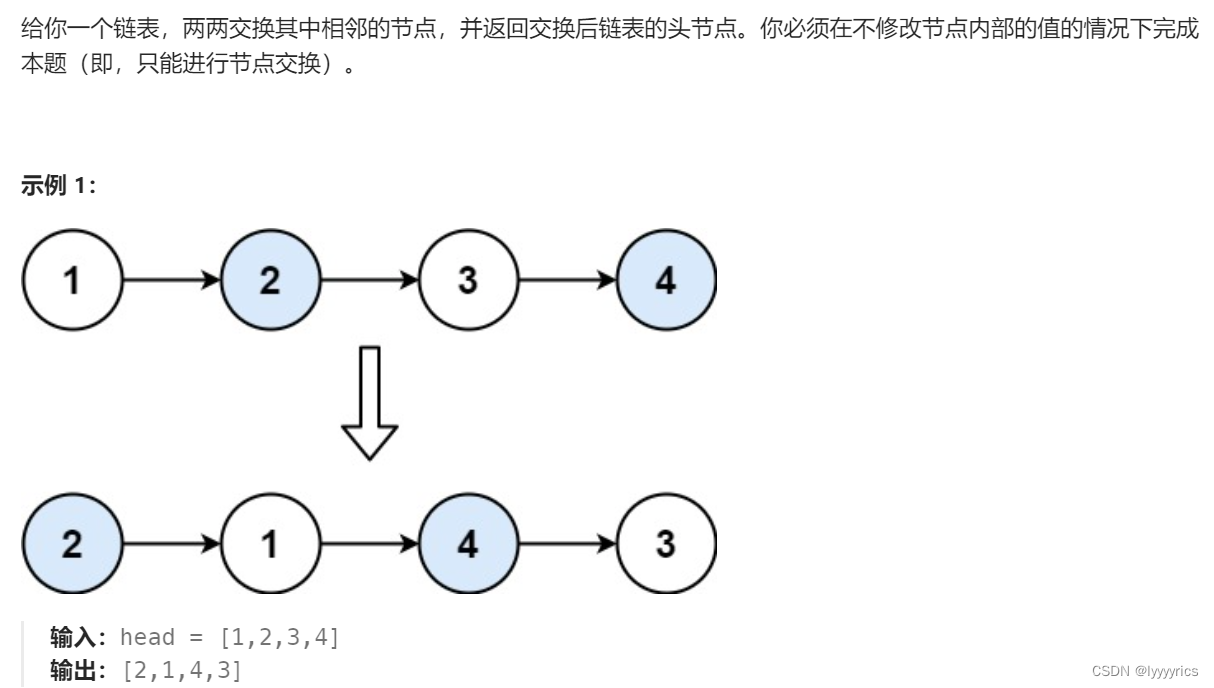
4.兩兩交換鏈表中的節點

問題分析

這里這道題和上一道題其實很相似，我們其實只需要將后面所有應該交換的節點全部交換了，然后將后面節點的新的頭給前面兩個節點連接上即可，注意這里后面是怎么交換的我們也不知道，但是我們用一個函數去讓他交換，我們讓他交換前兩個節點后面剩下的節點，它會轉換成叫喚后面剩下的節點除了前兩個節點外的剩下的節點，這樣一直遞歸下去，直到遇到遞歸出口為止。

函數頭
函數頭：dfs(head)

函數體
注意這里我們返回的交換之后鏈表的新的頭，意思就是當我們把除了1和2節點外的所有節點外的節點交換之后，會返回一個新的節點，注意看上面給出的示例，意思就是當我們用一個遞歸表示的話，返回的就是4這個節點，所以我們可以直接用tmp存儲這個節點，然后將前面兩個節點的指向進行變化即可。
函數體：

ListNode*tmp=swapPairs(head->next->next);
auto next=head->next;
head->next->next=head;
head->next=tmp;

遞歸出口
這里的遞歸出口還是當遇到空節點或者下一個節點是空節點直接返回當前節點

代碼展示

class Solution {
public:ListNode* swapPairs(ListNode* head) {if(head==nullptr||head->next==nullptr){return head;}ListNode*tmp=swapPairs(head->next->next);auto next=head->next;head->next->next=head;head->next=tmp;return next;}
};