特殊數組Ⅰ

如果數組的每一對相鄰元素都是兩個奇偶性不同的數字，則該數組被認為是一個?特殊數組?。

Aging 有一個整數數組?nums。如果?nums?是一個?特殊數組?，返回?true，否則返回?false。

示例 1：

輸入：nums = [1]

輸出：true

解釋：

只有一個元素，所以答案為?true。

示例 2：

輸入：nums = [2,1,4]

輸出：true

解釋：

只有兩對相鄰元素：?(2,1)?和?(1,4)，它們都包含了奇偶性不同的數字，因此答案為?true。

示例 3：

輸入：nums = [4,3,1,6]

輸出：false

解釋：

nums[1]?和?nums[2]?都是奇數。因此答案為?false。

提示：

• 1 <= nums.length <= 100
• 1 <= nums[i] <= 100

? ? ? ? 比較暴力，可以直接判斷相鄰的元素的奇偶性，如果相同返回False，如果檢查沒有的話，返回True。

代碼如下：

class Solution:def isArraySpecial(self, nums: List[int]) -> bool:for x,y in pairwise(nums):if x%2 == y%2:return Falsereturn True

特殊數組Ⅱ

如果數組的每一對相鄰元素都是兩個奇偶性不同的數字，則該數組被認為是一個?特殊數組?。

周洋哥有一個整數數組?nums?和一個二維整數矩陣?queries，對于?queries[i] = [fromi, toi]，請你幫助周洋哥檢查子數組?nums[fromi..toi]?是不是一個?特殊數組?。

返回布爾數組?answer，如果?nums[fromi..toi]?是特殊數組，則?answer[i]?為?true?，否則，answer[i]?為?false?。

示例 1：

輸入：nums = [3,4,1,2,6], queries = [[0,4]]

輸出：[false]

解釋：

子數組是?[3,4,1,2,6]。2 和 6 都是偶數。

示例 2：

輸入：nums = [4,3,1,6], queries = [[0,2],[2,3]]

輸出：[false,true]

解釋：

1. 子數組是?[4,3,1]。3 和 1 都是奇數。因此這個查詢的答案是?false。
2. 子數組是?[1,6]。只有一對：(1,6)，且包含了奇偶性不同的數字。因此這個查詢的答案是?true。

提示：

• 1 <= nums.length <= 105
• 1 <= nums[i] <= 105
• 1 <= queries.length <= 105
• queries[i].length == 2
• 0 <= queries[i][0] <= queries[i][1] <= nums.length - 1

?????????直接暴力去解決會超時，因為暴力的解法是O(n^2)，而數據范圍是1e5。

????????換一種考慮的方法，既然是要考慮相鄰的元素之間的奇偶性，不妨直接考慮他們之間的“逗號”。

? ? ? ? 比如說例子——

? ? ? ? 4， 3， 1， 6

? ? ? ? 我們去考慮每個逗號兩側的數字的奇偶性的相同，如果是相同的話，記為0，不同的話記為1.

? ? ? ? 那么就是這樣——

? ? ? ? 0， 1， 0

做個圖：

? ? ? ? 但是我們是需要去查詢一段區間內是否有這種特殊的數組，不難想到使用前綴和的方法。

? ? ? ? 查詢的時候發現需要加一個前導0.

? ? ? ? 原理就是只要這個區間的兩端的端點的前綴和不相等就是False，反之就是True。

代碼如下：

class Solution:def isArraySpecial(self, nums: List[int], queries: List[List[int]]) -> List[bool]:s = [0]for x,y in pairwise(nums):s.append(s[-1]+(x%2==y%2))return [s[f] == s[t] for f,t in queries]

所有數對中數位不同之和

車爾尼有一個數組?nums?，它只包含?正?整數，所有正整數的數位長度都?相同?。

兩個整數的?數位不同?指的是兩個整數?相同?位置上不同數字的數目。

請車爾尼返回?nums?中?所有?整數對里，數位不同之和。

示例 1：

輸入：nums = [13,23,12]

輸出：4

解釋：
計算過程如下：
-?13 和?23 的數位不同為?1 。
- 13?和 12?的數位不同為?1 。
-?23?和?12?的數位不同為?2 。
所以所有整數數對的數位不同之和為?1 + 1 + 2 = 4?。

示例 2：

輸入：nums = [10,10,10,10]

輸出：0

解釋：
數組中所有整數都相同，所以所有整數數對的數位不同之和為 0 。

提示：

• 2 <= nums.length <= 105
• 1 <= nums[i] < 109
• nums?中的整數都有相同的數位長度。

? ? ? ? 題目中說明，只包含有正整數，并且正整數的數位長度是相同的，需要我們返回的是所有正數中不同數位之和。

? ? ? ? 把所有的數位分開來考慮，舉個例子——

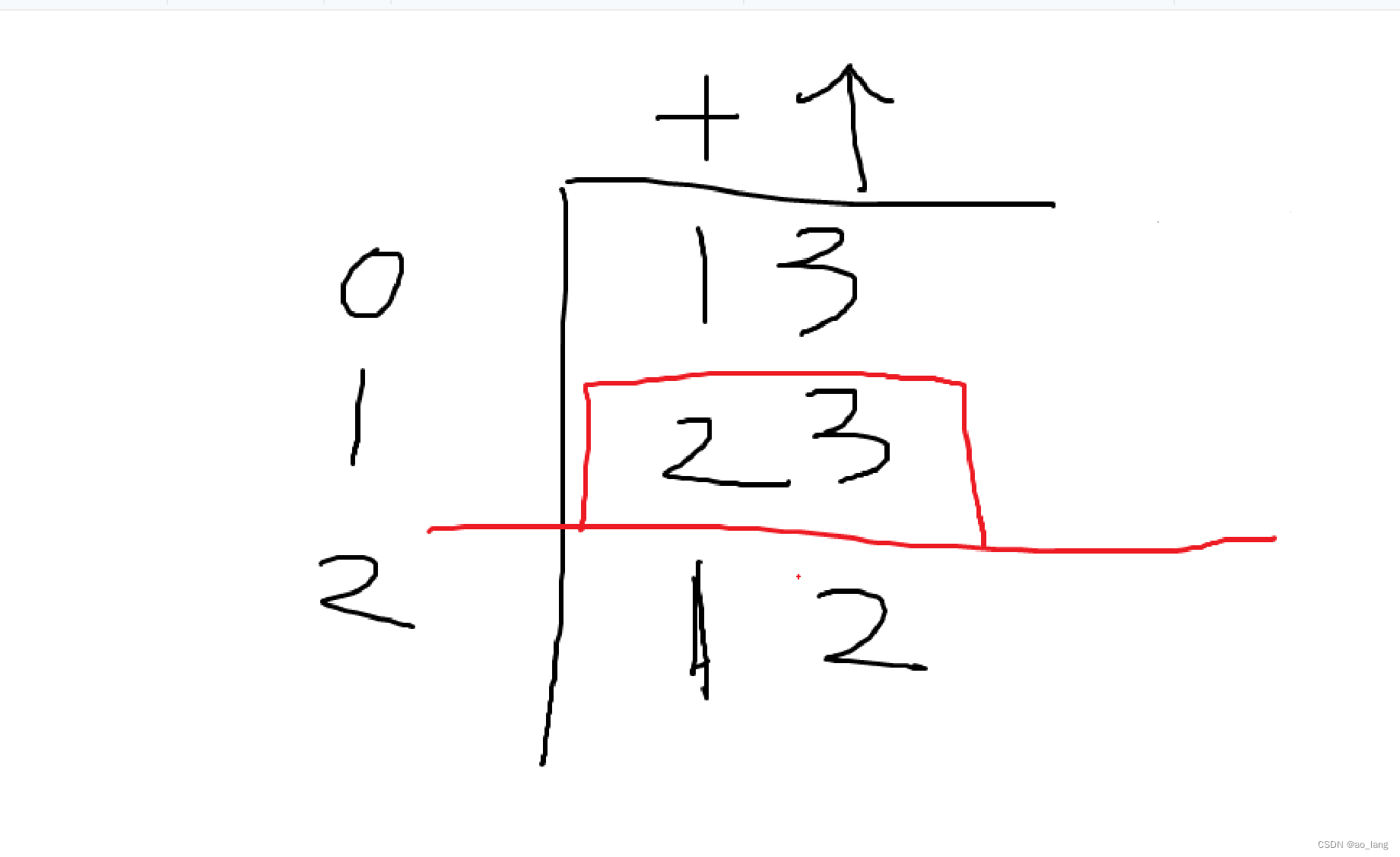
? ? ? ? 假如說現在已經考慮到了第1個數（下標為1）的各位，不妨把所有的各位抽出來看看如何計算。

????????

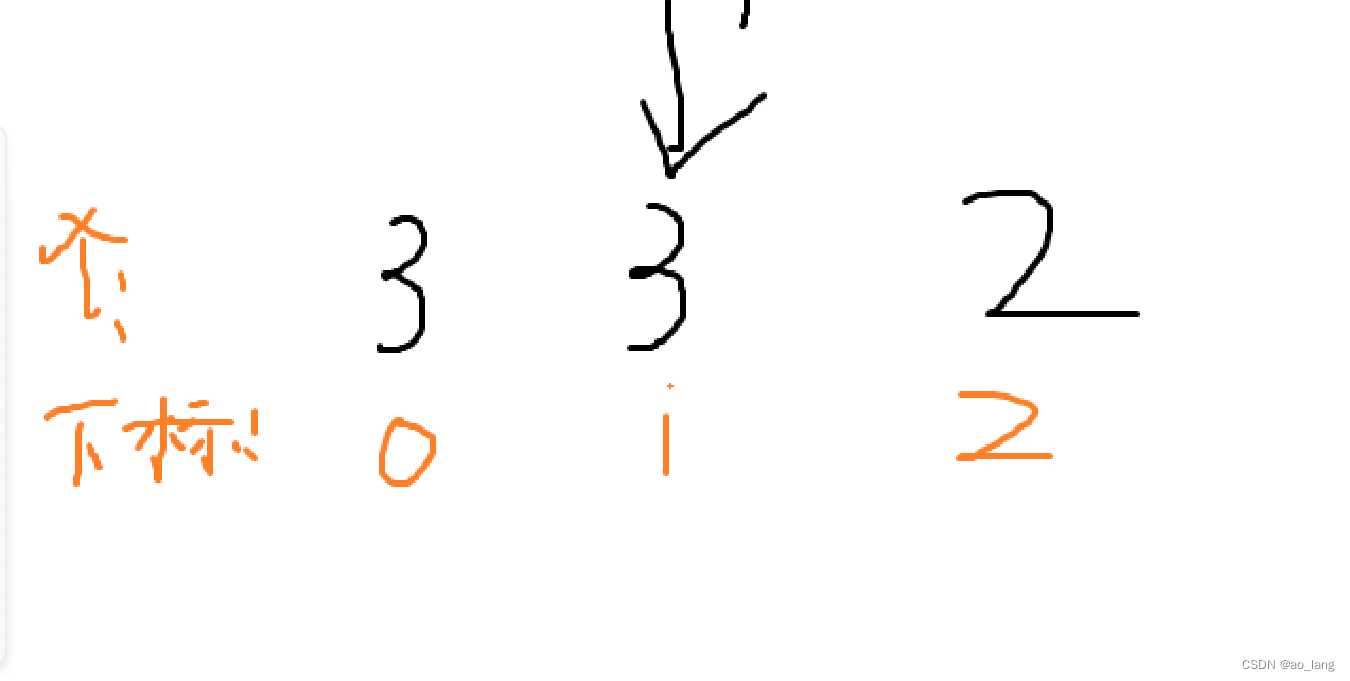
? ? ? ? 箭頭所指向的3，就是我們當前考慮到的地方，那么是如何進行考慮的呢？

? ? ? ? 因為我們是要統計每個數字的每一位的不同的數量，下標剛好就是在我們當前這個位置一共有多少個數字，我們可以搞一個哈希表，來統計在我們這個位置之前的，這個位置的值出現的次數。

? ? ? ? 又因為這個值只會是【0，9】，所以完全可以使用數組來模擬。

class Solution:def sumDigitDifferences(self, nums: List[int]) -> int:ans = 0cnt = [[0]*10 for _ in str(nums[0])]for k,x in enumerate(nums):for i,v in enumerate(map(int,str(x))):ans += k - cnt[i][v]cnt[i][v]+=1return ans

????????

到達第 K 級臺階的方案數

給你有一個?非負?整數?k?。有一個無限長度的臺階，最低?一層編號為 0 。

虎老師有一個整數?jump?，一開始值為 0 。虎老師從臺階 1 開始，虎老師可以使用?任意?次操作，目標是到達第?k?級臺階。假設虎老師位于臺階?i?，一次?操作?中，虎老師可以：

• 向下走一級到?i - 1?，但該操作?不能?連續使用，如果在臺階第 0 級也不能使用。
• 向上走到臺階?i + 2jump?處，然后?jump?變為?jump + 1?。

請你返回虎老師到達臺階?k?處的總方案數。

注意?，虎老師可能到達臺階?k?處后，通過一些操作重新回到臺階?k?處，這視為不同的方案。

示例 1：

輸入：k = 0

輸出：2

解釋：

2 種到達臺階 0 的方案為：

• 虎老師從臺階?1 開始。
  • 執行第一種操作，從臺階 1 向下走到臺階 0 。
• 虎老師從臺階 1 開始。
  • 執行第一種操作，從臺階 1 向下走到臺階 0 。
  • 執行第二種操作，向上走 20?級臺階到臺階 1 。
  • 執行第一種操作，從臺階 1 向下走到臺階 0 。

示例 2：

輸入：k = 1

輸出：4

解釋：

4 種到達臺階 1 的方案為：

• 虎老師從臺階 1 開始，已經到達臺階 1 。
• 虎老師從臺階 1 開始。
  • 執行第一種操作，從臺階 1 向下走到臺階 0 。
  • 執行第二種操作，向上走 20?級臺階到臺階 1 。
• 虎老師從臺階 1 開始。
  • 執行第二種操作，向上走 20?級臺階到臺階 2 。
  • 執行第一種操作，向下走 1 級臺階到臺階 1 。
• 虎老師從臺階 1 開始。
  • 執行第一種操作，從臺階 1 向下走到臺階 0 。
  • 執行第二種操作，向上走?20?級臺階到臺階 1 。
  • 執行第一種操作，向下走 1 級臺階到臺階 0 。
  • 執行第二種操作，向上走 21?級臺階到臺階 2 。
  • 執行第一種操作，向下走?1 級臺階到臺階 1 。

提示：

• 0 <= k <= 10^9

? ? ? ? 先來解釋一下這個題目的意思，說是最小的階梯是0，從1階梯開始，要求我們走到k階梯，有兩種操作，但是是有條件的。

? ? ? ? 操作一：向下走一級

? ? ? ? 操作二：向上走 2^jump 級

? ? ? ? 那么很容易想到使用暴力搜索改成記憶化的方法來求解。

? ? ? ? 畫一個圖來幫助我們理解一下——

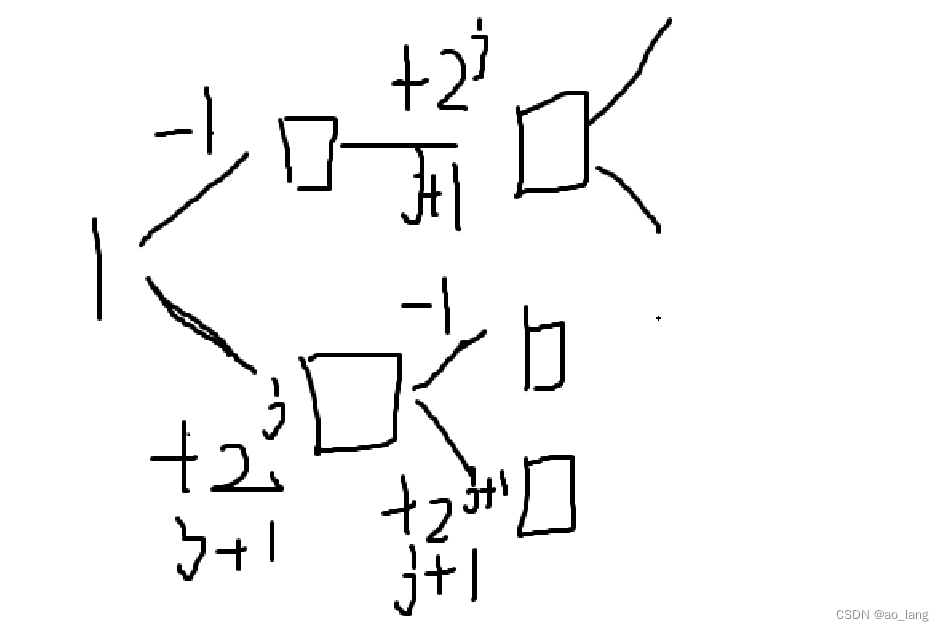
? ? ? ? 那么遞歸的出口又在哪里呢？

? ? ? ? 這需要我們在來分析一下了——

? ? ? ? 首先，分析出一個原理，在遞歸的過程中，數字 i 是逐漸變大的。

? ? ? ? 當 i 已經等于 k 的時候我們不能結束，因為他繼續搜下去可能會再有一個答案。

? ? ? ? 當 i 等于 k + 1 的時候我們還不能結束，因為這個時候只要執行了操作一就可以給結果再加上一個一，變成 i 等于 k，回到第一點。

? ? ? ? 當 i 等于 k+2的時候，我們就可以結束了，因為這個時候無論如何 i 都不可能能等于 k 了，直接返回0即可。

? ? ? ? 還有一點值得注意的就是我們需要再參數中加上一個bool類型的變量，用來說明喔當前這種情況是否是兩個操作都可以做。

最后代碼如下：

class Solution:def waysToReachStair(self, k: int) -> int:@cachedef dfs(i:int,j:int,p:bool)->int:if i >= k+2:return 0ans = 1 if i==k else 0ans += dfs(i+(1<<j),j+1,True)if p:ans += dfs(i-1,j,False)return ansreturn dfs(1,0,True)

?