一、什么是PID

PID（Proportional-Integral-Derivative）是一種經典的控制算法，廣泛應用在自動化控制系統中。它是通過對被控對象的測量值和設定值進行比較，并根據誤差的大小來調整輸出信號，實現對被控對象的穩定控制。

PID控制器由三個部分組成：比例控制器（P）、積分控制器（I）和微分控制器（D）。這三個部分分別對應了控制系統中的比例、積分和微分操作。

首先，我們來看比例控制器（P）。比例控制器根據被控對象當前的偏差與設定值之間的比例關系來調整輸出信號。假設被控對象的偏差為e，比例增益為Kp，那么比例控制器的輸出信號為Kp * e。比例控制器主要用于快速響應系統的初始偏差，但可能會導致系統存在超調和穩態誤差。

接下來是積分控制器（I）。積分控制器根據被控對象偏差的累積值來調整輸出信號，以消除穩態誤差。假設被控對象的偏差累積值為∑e，積分增益為Ki，那么積分控制器的輸出信號為Ki * ∑e。積分控制器主要用于消除系統的穩態誤差，但如果增益過大，可能會導致系統出現震蕩或不穩定的情況。

最后是微分控制器（D）。微分控制器根據被控對象偏差的變化率來調整輸出信號，以抑制系統的超調和振蕩。假設被控對象的偏差變化率為de/dt，微分增益為Kd，那么微分控制器的輸出信號為Kd * (de/dt)。微分控制器主要用于提高系統的穩定性和響應速度，但如果增益過大，可能會引入噪聲或造成系統震蕩。

PID控制器的輸出信號是這三個部分的總和：輸出信號 = Kp * e + Ki * ∑e + Kd * (de/dt)。實際應用中，可以通過試驗和經驗來確定適當的增益參數，以達到所需的控制效果。

總結一下，PID控制器是一種常用的控制算法，通過比例、積分和微分操作來調整輸出信號，實現對被控對象的穩定控制。它在工業、自動化等領域廣泛應用，能夠有效地解決許多控制問題。然而，在實際應用中需要根據具體情況調整參數，以獲得最佳的控制效果。

學過自動控制原理的對PID并不陌生，PID控制是對偏差信號e(t)進行比例、積分和微分運算變換后形成的一種控制規律。PID 算法的一般形式：

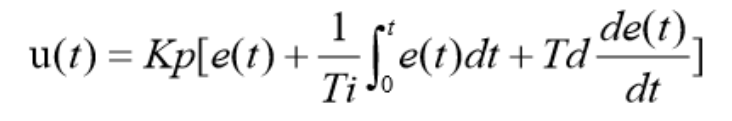
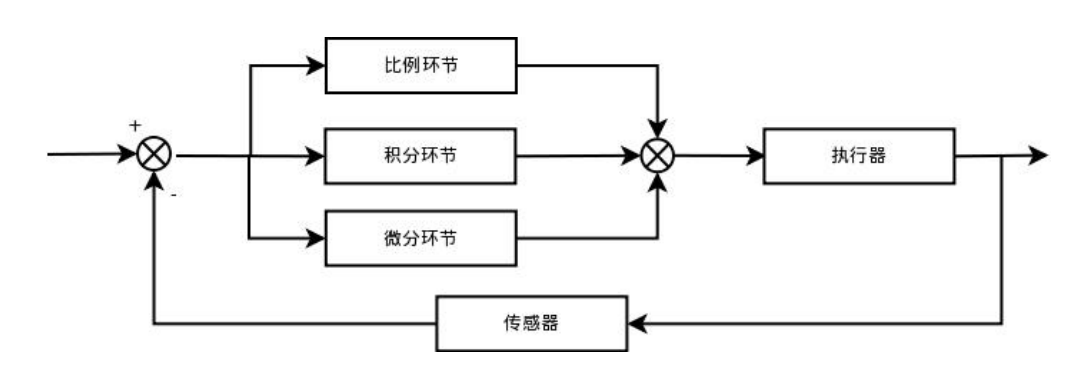
• PID控制系統原理框圖

  

---

二、PID離散化

在實際應用中，PID控制器通常需要在數字系統中進行離散化處理。離散化是將連續時間域的PID控制器轉換為離散時間域的控制器，以適應數字控制系統的要求。

離散化PID控制器的關鍵在于將連續時間域的微分和積分操作轉換為離散時間域的形式。下面介紹一種常用的離散化方法：采樣周期法（也稱為Z變換法）。

1. 采樣周期（Sampling Period）：首先確定控制系統的采樣周期，即每次對被控對象進行測量和調整輸出的時間間隔。

2. 離散化比例項（Discretization of the Proportional Term）：離散化比例項可以簡單地通過乘以采樣周期得到。離散比例增益Kp_discrete = Kp * T（其中Kp為連續比例增益，T為采樣周期）。

3. 離散化積分項（Discretization of the Integral Term）：離散化積分項可以使用數值積分方法來實現，常用的方法是離散化誤差的累加。離散積分增益Ki_discrete = Ki * T（其中Ki為連續積分增益，T為采樣周期）。

4. 離散化微分項（Discretization of the Derivative Term）：離散化微分項可以使用數值微分方法來實現，常用的方法是差分運算。離散微分增益Kd_discrete = Kd / T（其中Kd為連續微分增益，T為采樣周期）。

5. 離散化PID控制器（Discretization of the PID Controller）：將離散化的比例項、積分項和微分項相加，得到離散化的PID控制器輸出信號。離散化PID控制器的輸出信號為PID_discrete = Kp_discrete * e + Ki_discrete * ∑e + Kd_discrete * (de/dt)。

通過以上離散化方法，我們可以將連續時間域的PID控制器轉換為離散時間域的控制器，方便在數字控制系統中實現。

需要注意的是，在離散化過程中可能會引入一定的誤差，特別是在采樣周期較大或被控對象響應速度較快的情況下。因此，在實際應用中，需要根據系統的要求和性能指標進行參數調節和系統優化，以獲得最佳的離散化PID控制效果。

對PID連續系統離散化，從而方便在處理器上實現，PID 離散表示形式：

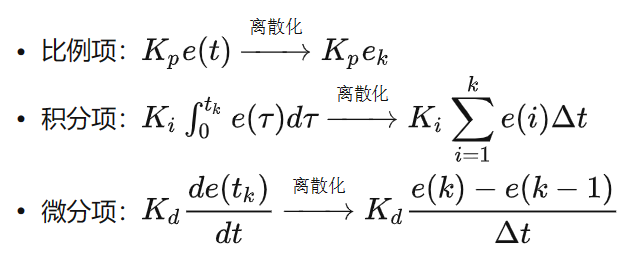
離散化后最終得到位置式PID：

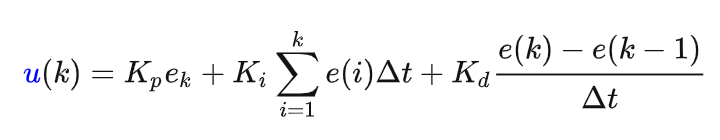
u(k)為控制器輸出的控制量;（輸出）
e(k)為偏差信號，它等于給定量與輸出量之差；（輸入）
Kp 為比例系數；
Ti 為積分時間常數；
Td 為微分時間常數。

---

1. 位置式PID公式

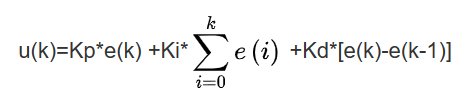
2. 增量式PID公式

---

三、兩種PID的不同點

• 位置式
  是一種非遞推算法，輸出值U(k)和執行機構的實際位置一一對應，在不帶積分部件的對象中可以很好的應用。但是每次輸出均與過去的狀態有關，計算量大。
• 增量式
  輸出的是增量，控制增量的值僅與最近3次采樣值有關，不需要累計偏差，運算量小，計算錯誤影響小。但會積分截斷效應大，有穩態誤差。

---

四、C語言程序實現

• pid.c

#include "pid.h"/*定義PID參數結構體*/
typedef struct _PID
{float Kp,Ki,Kd;//比例系數、積分系數、微分系數float SetValue,ActualValue;//目標值、實際值float Error;//第K次誤差float LastError;//第K-1次誤差float PreError;//第K-2次誤差float SumError;//累計偏差float Integral,MaxI;//積分、積分限幅float Output,MaxOut;//輸出、輸出限幅
}PID;/************************************************
*@brief  ：位置式PID控制器
*@param  ：PID結構體變量地址,當前實際值
*@retval : 期望輸出值
*************************************************/
int32_t Position_PID_Control(PID *pid,float Cur_Value)
{pid->Error=pid->SetValue-Cur_Value; //計算偏差      pid->SumError +=pid->Error;//累計偏差pid->ActualValue=(pid->Kp*(pid->Error-pid->LastError))//比例環節+(pid->Ki*pid->SumError)//積分環節+(pid->Kd*(pid->Error-pid->LastError);//微分環節pid->LastError=pid->Error;return ((int32_t)pid->ActualValue); //返回計算值	 
}/************************************************
*@brief  ：速度閉環PID控制
*@param  ：PID結構體變量地址,當前實際值
*@retval : 期望輸出值
*************************************************/
int32_t Inc_Pid_Ctrl(PID *pid,float Cur_Value)
{pid->Error=pid->SetValue-Cur_Value; //計算偏差pid->ActualValue +=(pid->Kp*(pid->Error-pid->LastError))//比例環節+(pid->Ki*(pid->Error))//積分環節+(pid->Kd*(pid->Error-2*pid->LastError+pid->PreError));//微分環節 pid->PreError=pid->LastError;//存儲偏差，進行下次計算                                                             pid->LastError=pid->Error;                                                            	return ((int32_t)pid->ActualValue); //返回計算值
}