決策樹、ID3決策樹（信息熵、信息增益）

目錄

一、決策樹簡介

決策樹建立過程

二、ID3決策樹

核心思想：決策樹算法通過計算??信息增益??來選擇最佳分裂特征

1、信息熵

2、信息熵的計算方法

3、信息增益

4、信息增益的計算（難點）

5、ID3決策樹構建案例

三、總結

一、決策樹簡介

????????決策樹 (Decision Tree) 是一種??樹形結構的預測模型??，它代表的是對象屬性與對象值之間的一種映射關系。決策樹通過學習數據特征，構建一套層次化的“判斷-分支”規則，最終在葉子節點給出預測結果（每個葉子節點代表一種分類結果）。

根節點 (Root Node)??：代表整個數據集的起始點，包含所有樣本。

內部節點 (Internal Node)??：對應特征或屬性上的判斷條件，每個判斷會產生分支。

葉節點 (Leaf Node)??：代表決策的最終結果，即分類的類別或回歸的預測值。

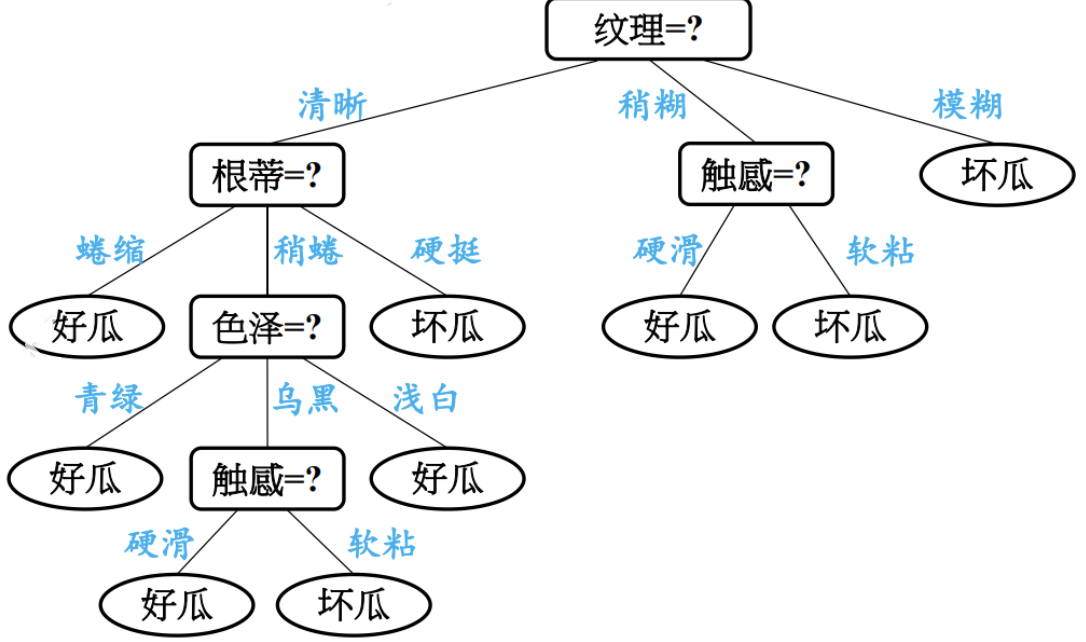
決策樹建立過程

構建決策樹的核心是??遞歸地選擇最優特征??對數據進行劃分，目標是使劃分后子集的“純度”最高。

????????1.特征選擇：選取有較強分類能力的特征。

????????2.決策樹生成：根據選擇的特征生成決策樹。

????????3. 決策樹也易過擬合，采用剪枝的方法緩解過擬合。

二、ID3決策樹

????????ID3（Iterative Dichotomiser 3）是一種經典的決策樹學習算法，由 Ross Quinlan 在 1986 年提出，主要用于分類問題。它通過??信息增益??來選擇特征進行劃分，構建樹形結構，其核心目標是生成一棵盡可能小的決策樹（奧卡姆剃刀原理）。

核心思想：決策樹算法通過計算??信息增益??來選擇最佳分裂特征

計算當前數據集的初始信息熵（Entropy），衡量數據的混亂程度或不確定性
針對每個特征，計算其信息增益。信息增益表示使用該特征劃分數據后，不確定性減少的程度
選擇信息增益最大的特征??作為當前節點的劃分標準
根據該特征的每個取值，將數據集劃分為不同的子集，并為每個子集創建新的子節點
對每個子節點??遞歸地重復??上述過程，直到滿足停止條件（如所有樣本屬于同一類別，或沒有更多特征可用）

1、信息熵

????????熵 Entropy ：信息論中代表隨機變量不確定度的度量

????????熵越大，數據的不確定性度越高，信息就越多（有序向無序變化）
????????熵越小，數據的不確定性越低

2、信息熵的計算方法

$H(x) = -\sum_{i=0}^n P(x_i)log_2P(x_i)$

總的熵 = 各個熵的累加和

?????其中 $P(xi)$ 表示數據中類別出現的概率，H(x) 表示信息的信息熵值，信息熵的單位是??比特?? (bit)

舉例

????????計算數據 α（ABCDEFGH）信息熵，其中A、B、C、D、E、F、G、H 出現的概率為：1/8

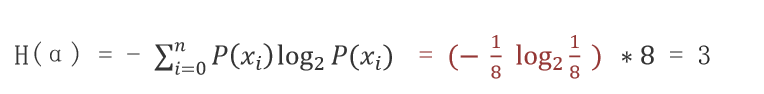
????????計算數據 β（AAAABBCD）信息熵，其中A 出現的概率為1/2，B 出現的概率為1/4，C、D 出現的概率為1/8

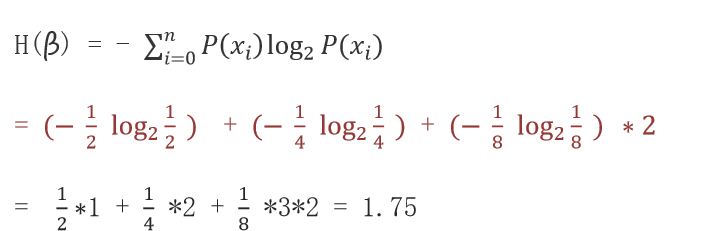
3、信息增益

????????信息增益衡量的是，在知道某個特征的信息之后，目標變量的??不確定性減少的程度??。它的核心思想比較知道特征前后不確定性的變化。

????????信息增益??就是??初始熵與條件熵的差值??。這個差值越大，說明該特征對于降低目標變量不確定性的貢獻越大，也就越重要。

????????條件熵??描述了在已知第二個隨機變量?Y的值的前提下，隨機變量?X的??剩余不確定性??或信息熵?。換句話說，它表示在我們已經知道?Y的一些信息后，要完全確定?X的值還需要多少額外的信息。

4、信息增益的計算（難點）

$g(D, a) = H(D)-H(D|A)$ ，即信息增益 = 熵 - 條件熵

熵看標簽，條件熵看特征和標簽

????????條件熵的計算

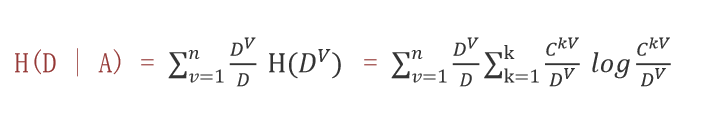
舉例計算

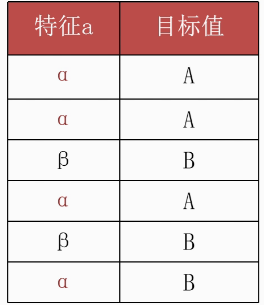
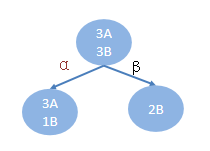
已知6個樣本，根據特征a：

α 部分對應的目標值為： AAAB

β 部分對應的目標值為：BB? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

解析：一共6個樣本，下面有兩個類別：α和β

????????1、計算信息熵： $H(x) = -\sum_{i=0}^n P(x_i)log_2P(x_i)$

A的信息熵 =? $-\frac{3}{6}log_{2}(\frac{3}{6})$

B的信息熵 =? $-\frac{3}{6}log_{2}(\frac{3}{6})$

信息熵 =? $-\frac{3}{6}log_{2}(\frac{3}{6})$ ?× 2 = 1

????????2、計算條件熵（條件熵 = 每個自己的信息熵 × 在整個數據集占比的概率）

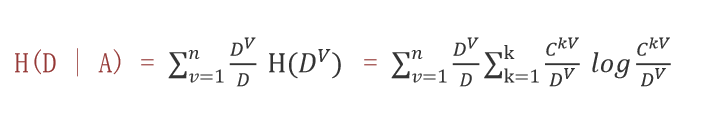
α 的條件熵 =? $-\frac{1}{4}log_{2}\frac{1}{4}+ -\frac{3}{4}log_{2}\frac{3}{4} =0.81$

β的條件熵 =? $-\frac{2}{2}log_{2}\frac{2}{2} =0$

條件熵 =? $\frac{4}{6}\times 0.81+\frac{2}{6}\times 0=0.54$

????????3、計算：信息增益 = 熵 - 條件熵

信息增益? $= 1 - 0.54 = 0.46$

????????至此計算完了特征a的信息增益，以此類推計算其他特征列的信息增益。

????????與其他列相比，誰大誰當根節點。

5、ID3決策樹構建案例

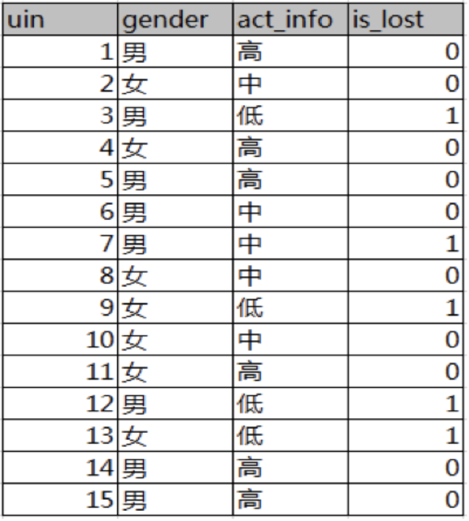
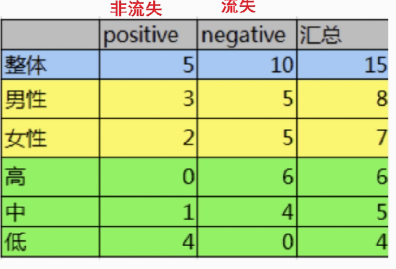
已知? 某一個論壇客戶流失率數據

需求：考察性別、活躍度特征哪一個特征對流失率的影響更大

分析：

?????15條樣本：5個正樣本、10個負樣本

計算熵
計算性別信息增益
計算活躍度信息增益
?比較兩個特征的信息增益

????????結論：活躍度的信息增益比性別的信息增益大，對用戶流失的影響比性別大。由此可知，偏向于選擇種類多的特征作為分裂依據。

三、總結

????????ID3算法是決策樹家族的奠基性算法，它通過??信息增益??選擇特征來構建樹形分類模型。雖然它存在對連續特征和不完整數據支持不佳、容易過擬合等局限，但其核心思想清晰且易于理解，為后續更強大的算法（如C4.5和CART）奠定了基礎。

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/web/95713.shtml
繁體地址，請注明出處：http://hk.pswp.cn/web/95713.shtml
英文地址，請注明出處：http://en.pswp.cn/web/95713.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！