在解決螺旋矩陣問題時，我們需要按照順時針螺旋順序遍歷矩陣，并返回所有元素。本文將分享兩種高效的解決方案：邊界收縮法和方向模擬法。

題目描述

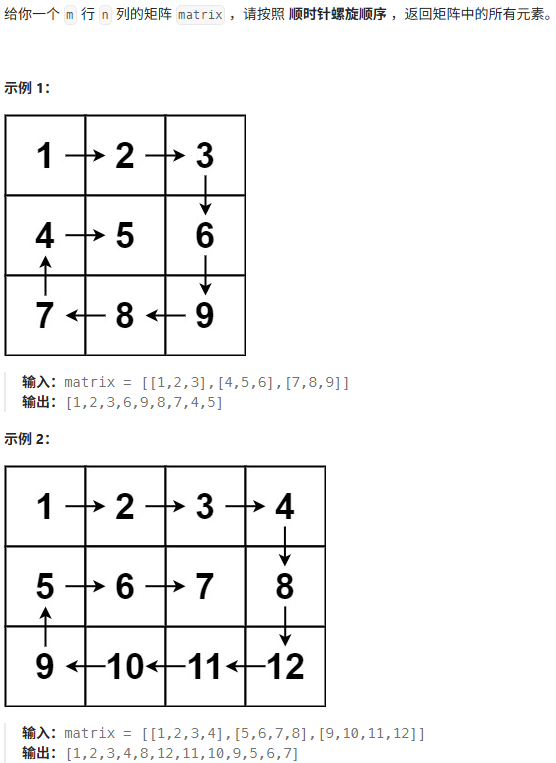
邊界收縮法

邊界收縮法通過定義四個邊界（上、下、左、右）來模擬螺旋遍歷的過程。每完成一個方向的遍歷，就收縮對應的邊界，直到所有元素被訪問完畢。

算法思路

1. 初始化邊界：top = 0,?bottom = m-1（行數-1）,?left = 0,?right = n-1（列數-1）。
2. 按層遍歷：
   • 向右：遍歷上邊界（top行），從?left?到?right。
   • 向下：遍歷右邊界（right列），從?top+1?到?bottom。
   • 向左：遍歷下邊界（bottom行），從?right-1?到?left+1（需確保存在內層）。
   • 向上：遍歷左邊界（left列），從?bottom?到?top+1（需確保存在內層）。
3. 收縮邊界：完成一圈后，將?top++,?bottom--,?left++,?right--。
4. 終止條件：當邊界交錯時停止（top > bottom?或?left > right）。

代碼實現

class Solution {public List<Integer> spiralOrder(int[][] matrix) {List<Integer> result=new ArrayList<Integer>();int x= matrix.length;int y=matrix[0].length;int left=0;int right=y-1;int top=0;int bottom=x-1;while(left<=right&&top<=bottom){for(int i=left;i<=right;i++){result.add(matrix[top][i]);}for(int i=top+1;i<=bottom;i++){result.add(matrix[i][right]);}if(left<right&&top<bottom) {for (int i = right - 1; i > left; i--) {result.add(matrix[bottom][i]);}for (int i = bottom; i > top; i--) {result.add(matrix[i][left]);}}left++;right--;top++;bottom--;}return result;}
}

復雜度分析

• 時間復雜度：O(m*n)，每個元素被訪問一次。
• 空間復雜度：O(1)，僅使用常量額外空間（結果列表不計入）。

方向模擬法（其他解決方案）

方向模擬法通過定義方向數組和記錄訪問狀態來模擬螺旋路徑，適合對邊界條件處理不熟悉的情況。

算法思路

1. 初始化：
   • 方向數組?dirs?表示右、下、左、上四個方向。
   • 訪問矩陣?visited?記錄元素是否被訪問。
   • 從?(0,0)?開始，初始方向為右。
2. 遍歷矩陣：
   • 將當前元素加入結果列表，并標記為已訪問。
   • 計算下一個位置，若越界或已訪問，則順時針轉向。
   • 更新位置并繼續遍歷，直到所有元素被訪問。

代碼實現

class Solution {public List<Integer> spiralOrder(int[][] matrix) {List<Integer> result = new ArrayList<>();if (matrix == null || matrix.length == 0) return result;int m = matrix.length, n = matrix[0].length;boolean[][] visited = new boolean[m][n];int[][] dirs = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}}; // 右、下、左、上int r = 0, c = 0, d = 0;int total = m * n;for (int i = 0; i < total; i++) {result.add(matrix[r][c]);visited[r][c] = true;// 計算下一個位置int nr = r + dirs[d][0];int nc = c + dirs[d][1];// 若越界或已訪問，則轉向if (nr < 0 || nr >= m || nc < 0 || nc >= n || visited[nr][nc]) {d = (d + 1) % 4; // 順時針轉向nr = r + dirs[d][0];nc = c + dirs[d][1];}r = nr;c = nc;}return result;}
}

復雜度分析

• 時間復雜度：O(m*n)，每個元素訪問一次。
• 空間復雜度：O(m*n)，visited?矩陣額外占用空間。

總結

• 邊界收縮法：通過動態調整邊界模擬螺旋路徑，無需額外空間，是更優解。
• 方向模擬法：直觀易理解，但需要額外空間記錄訪問狀態，適合快速實現。

兩種方法均能高效解決螺旋矩陣問題，實際應用中推薦優先使用邊界收縮法！