目錄
- 插入排序
- 例子
- 時間復雜度
- java代碼
- 希爾排序(縮小增量排序)
- 例子
- 時間復雜度
- java代碼
相關文章
- 學習數據結構理論+算法時間復雜度
- 學習有序二叉樹+平衡二叉樹+紅黑樹
- 學習冒泡排序+選擇排序并使用java寫代碼
- 學習插入排序+希爾排序并使用java寫代碼
- 學習堆排序+基數排序并使用java寫代碼
- 學習遞歸+歸并排序+快速排序并使用java寫代碼
插入排序:
- 認為數組當中的第一個數值是已經排好序的數值;
- 定義一個游標,從第二個數值開始不斷地向后進行遍歷;
- 游標指向的數值插入到已經拍好序的數組當中。
例子:
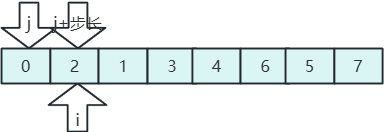
- 定義一個游標 i ,從第一個開始遍歷;
- 定義一個游標 j ,指向 i 的前一個數值;
- 對應的 j+1 指向要插入的數值;
- j 應當要比 j+1 小,如果 j > j+1 ,交換位置。
待排序組:5、7、4、1、3、0、2、6,用插入排序進行排序,步驟如下:

- j 指向5,j+1 指向7,5<7,不動;
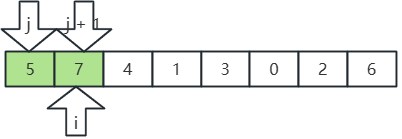
- 繼續,i, j,j+1 后移,
- j 指向7,j+1 指向4,7>4,交換位置;
- j 指向5,j+1 指向4,5>4,交換位置;
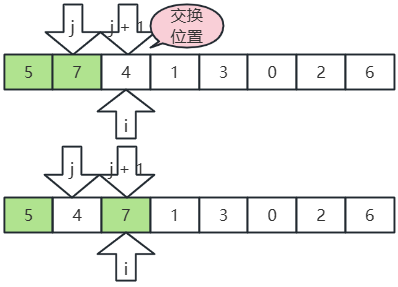
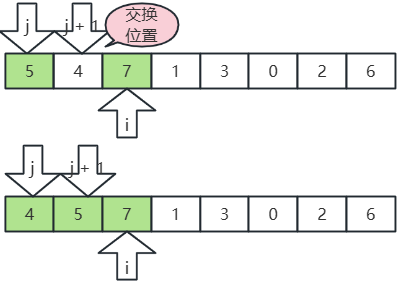
- 繼續,i, j,j+1 后移,
- j 指向7,j+1 指向1,7>2,交換位置;
- j 指向5,j+1 指向1,5>1,交換位置;
- j 指向4,j+1 指向1,4>1,交換位置;
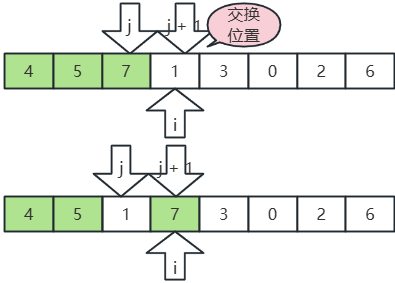
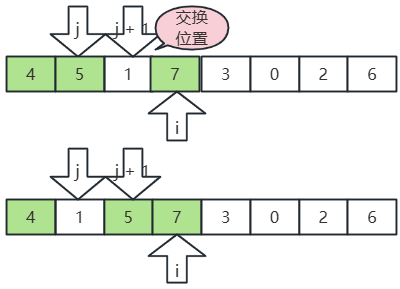
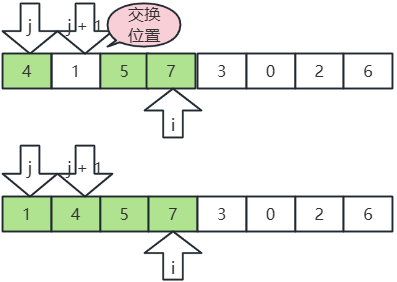
- 繼續,i, j,j+1 后移,
- j 指向7,j+1 指向3,7>3,交換位置;
- j 指向5,j+1 指向3,5>3,交換位置;
- j 指向4,j+1 指向3,4>3,交換位置;
- j 指向1,j+1 指向3,1<3,不動;
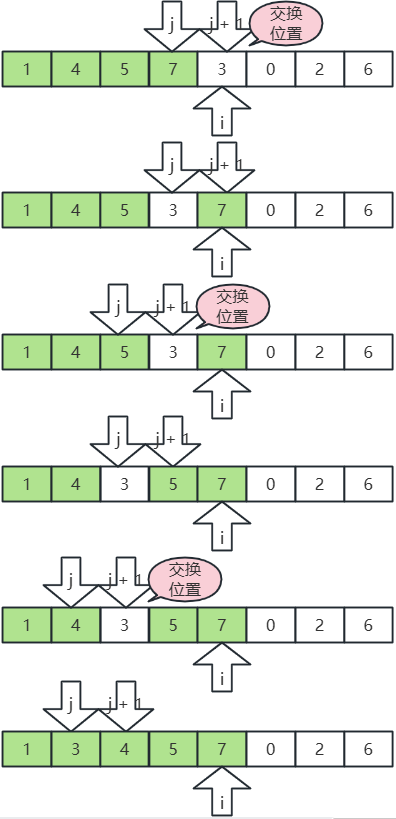
- ……
- 這樣一直交換插入,直到插入排序完成。
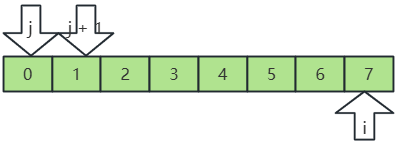
時間復雜度:
| 數據(默認從第二個數據開始) | 移動次數(理想情況沒有中斷) |
|---|---|
| 下標是1的數據 | 1 |
| 下標是2的數據 | 2 |
| 下標是3的數據 | 3 |
| 下表是4的數據 | 4 |
| …… | …… |
| 下標的x-1的數據 | x-1 |
等差數列求和公式:y=(1+x?1)(x?1)2y=\frac{(1+x-1)(x-1)}{2}y=2(1+x?1)(x?1)?
得到時間復雜度是:O(n2)O(n^2)O(n2)
缺點: 越小的數值在后面移動的次數越多
java代碼:
package com.xxx;import java.util.Arrays;//插入排序
public class InsertSort {public static void main(String[] args) {int[] arr = {5,7,4,1,3,0,2,6};sort(arr);System.out.println(Arrays.toString(arr));}public static void sort(int[] arr) {for(int i=1;i<arr.length;i++) {//i指向的數據插入到前邊已經拍好的數組當中for(int j=i-1;j>=0;j--) {//j 和 j+1 指向的數據進行比較,交換if(arr[j]>arr[j+1]) {int temp = arr[j];arr[j] = arr[j+1];arr[j+1] = temp;}else {break;}}}}
}
插入:
定義游標j指向i的前一個數據,j和j+1指向的數據進行交換,若j+1的值小,則j和j+1指向的值進行交換,j–;繼續比較,知道j+1的值大,或著j=0停止。
希爾排序(縮小增量排序):
- 將數組按照數組長度的一半為間隔(步長)進行分組(奇偶無所謂,第一組為3個,剩下的均是兩兩一組),組內進行插入排序
- 將數組按照數組長度的一半的一半為間隔進行分組,組內進行插入排序,多個分組來回交替插入排序;
- 將數組按照數組長度的一半的一半的一半為間隔進行分組,組內進行插入排序;
- ……
- 直到步長為1,整個數組作為一組,進行插入配許,結束。
例子:
待排序組:5、7、4、1、3、0、2、6,用希爾排序進行排序,步驟如下:
- 先分組:8個數值,8/2=4,每隔四個為一組;
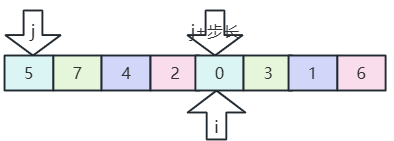
- 組內比較,排序:
- 5、0比較,交換位置;
- 7、3比較,交換位置;
- 4、1比較,交換位置;
- 2、6比較,位置不動;
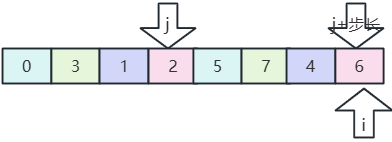
- 在分一半,步長為2;
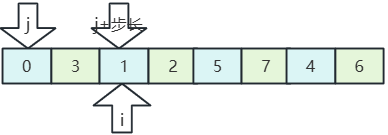
- 組內比較,排序(分組來回交替排序插入):
- 0、1比較,位置不動;
- 3、2比較,交換位置;
- 1、5比較,位置不動;
- 2、7比較,位置不動;
- 5、4比較,交換位置;
- 7、6比較,交換位置;
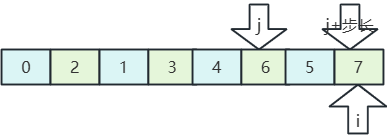
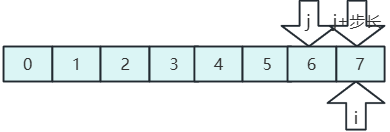
- 在分一半,步長為1,整個數組為一組;
- 比較排序,直到結束,希爾排序完成。
時間復雜度:
| 輪數 | 間隔 | 交換次數 |
|---|---|---|
| 第一輪 | x/2=x/21x/2=x/2^1x/2=x/21 | x/2x/2x/2 |
| 第二輪 | x/2/2=x/22x/2/2=x/2^2x/2/2=x/22 | x/2x/2x/2 ~ x?1x-1x?1 |
| 第三輪 | x/2/2/2=x/23x/2/2/2=x/2^3x/2/2/2=x/23 | x/2x/2x/2 ~ x?1x-1x?1 |
| 第四輪 | x/2/2/2/2=x/24x/2/2/2/2=x/2^4x/2/2/2/2=x/24 | x/2x/2x/2 ~ x?1x-1x?1 |
| …… | …… | …… |
| 第k輪 | 1=x/2k1=x/2^k1=x/2k | x?1x-1x?1 |
得到關系式:1=x/2k1=x/2^k1=x/2k
轉換:x=2kx=2^kx=2k
得到一個輪次的k與x的關系式是:k=logxk=logxk=logx
所有的輪次相加是:k=xlogxk=xlogxk=xlogx
得到時間復雜度是:O(nlogn)O(nlogn)O(nlogn)
java代碼:
package com.xxx;import java.util.Arrays;//希爾排序
public class ShellSort {public static void main(String[] args) {int[] arr = {17,7,24,33,28,19,15,30};sort(arr);System.out.println(Arrays.toString(arr));}public static void sort(int[] arr) {//定義步長變量 grpfor(int grp=arr.length/2;grp>=1;grp=grp/2) {//定義游標 i,控制 i 的移動,組內進行插入排序for(int i=grp;i<arr.length;i++) {//結束 j 和 j+grp 完成組內的插入for(int j=i-grp;j>=0;j=j-grp) {// j 和 j+grp 指向的數據進行比較,交換if(arr[j]>arr[j+grp]) {int temp = arr[j];arr[j] = arr[j+grp];arr[j+grp] = temp;}else {break;}}}}}
}


》)






驅動開發)





![[muduo網絡庫]-muduo庫TcpServer類解析](http://pic.xiahunao.cn/[muduo網絡庫]-muduo庫TcpServer類解析)



)