題目描述

解法一：暴力解

遍歷每一個可能的子串，然后逐一判斷每個子串中是否有重復字符。

具體步驟：

• 使用兩層嵌套循環來生成所有子串的起止位置：
  外層循環 i 從 0 到 n-1 (起始位置)。
  內層循環 j 從 i 到 n-1 (結束位置)。
• 對于每一個子串 s.substring(i, j+1)，我們再設計一個輔助函數 hasDuplicate(substring) 來檢查這個子串中是否存在重復字符。
• 檢查 hasDuplicate 通常需要使用一個哈希集合 (Set)：遍歷子串的每個字符，嘗試加入 Set。如果某個字符加入失敗（因為 Set 中已存在），則說明有重復。
• 如果沒有重復，我們就用 j - i + 1 來更新記錄的最大長度 max_len。

實現代碼

#include <unordered_set> // 用于哈希集合
#include <algorithm>     // 用于 std::max
class Solution {
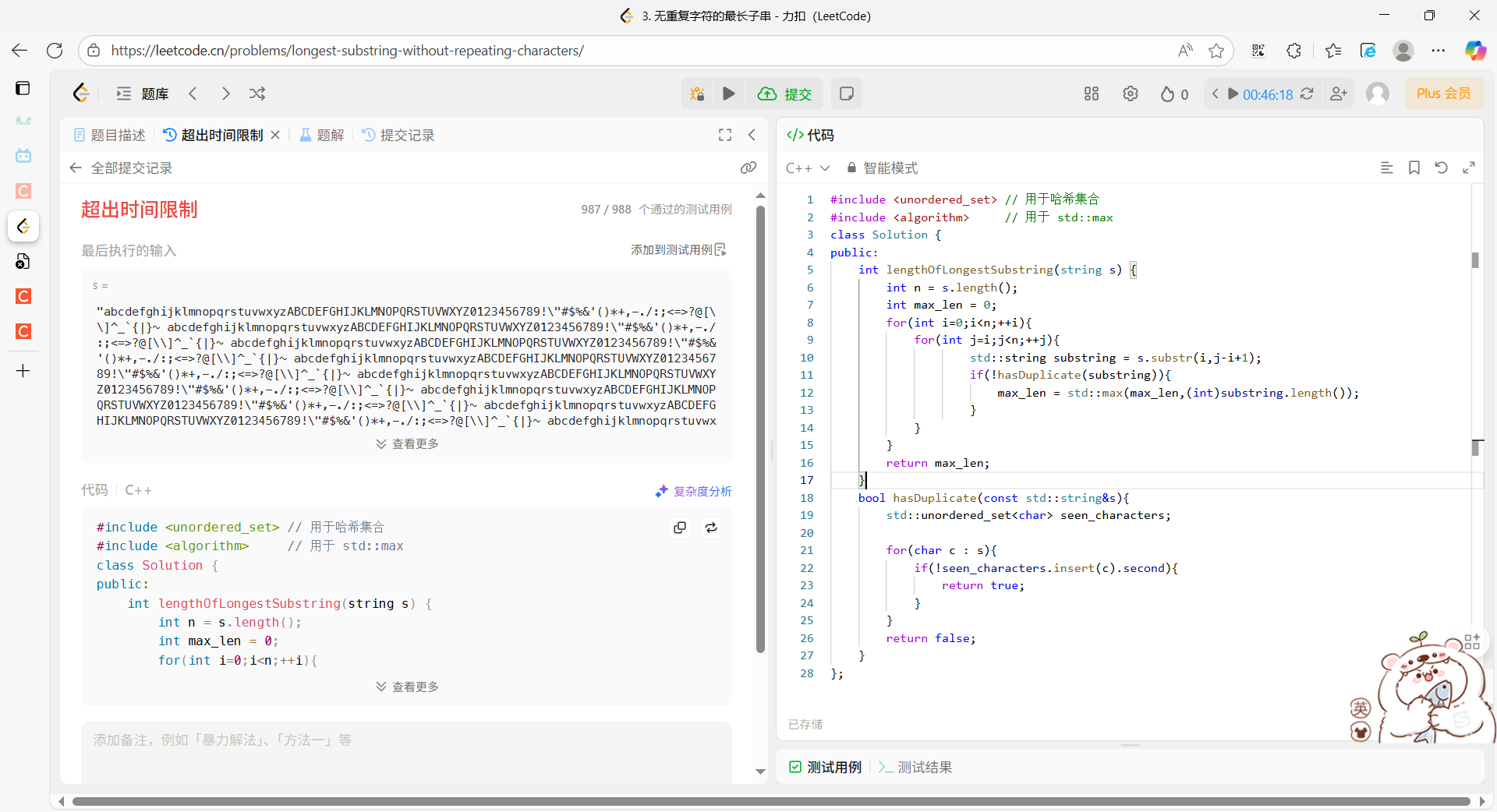
public:int lengthOfLongestSubstring(string s) {int n = s.length();int max_len = 0;for(int i=0;i<n;++i){for(int j=i;j<n;++j){std::string substring = s.substr(i,j-i+1);if(!hasDuplicate(substring)){max_len = std::max(max_len,(int)substring.length());}}}return max_len;}bool hasDuplicate(const std::string&s){std::unordered_set<char> seen_characters;for(char c : s){if(!seen_characters.insert(c).second){return true;}}return false;}
};

執行結果
超出時間范圍了

復雜度分析
時間：O(n^3)
空間：O(n)

解法二：滑動窗口

我們維護一個窗口 [start, end]，它始終代表一個不包含重復字符的子串。我們不斷嘗試擴大這個窗口的右邊界end。如果在這個過程中，新加入的字符導致了窗口內出現重復，我們就需要收縮窗口的左邊界 start，直到窗口內不再有重復字符為止。

如何快速判斷字符是否重復以及其位置？
我們需要一個數據結構來高效地完成兩件事：
判斷一個字符是否已經在當前窗口中。
如果存在，找出它上次出現的位置。
哈希映射 (Map) 或數組是完美的選擇。
哈希映射 Map<Character, Integer>：鍵 (Key) 存儲字符，值 (Value) 存儲該字符的最新索引。
數組 int[128]：如果字符集是 ASCII，我們可以用一個大小為 128 的數組來模擬哈希映射，數組的索引是字符的 ASCII 碼，值是該字符的最新索引。這比哈希映射更快。

具體步驟 (以哈希映射為例)：
初始化兩個指針：start = 0 (窗口左邊界)，end = 0 (窗口右邊界)。
初始化 max_len = 0 (記錄最大長度)。
初始化一個哈希映射 map，用于存儲窗口內字符及其最新索引。
使用 end 指針作為主循環，從 0 遍歷到 n-1：
a. 獲取當前右邊界的字符 char_end = s[end]。
b. 檢查 char_end 是否導致重復：
i. 在 map 中查找 char_end。
ii. 如果 char_end 已經在 map 中存在，并且它上次出現的位置 map.get(char_end) 在當前窗口內（即 map.get(char_end) >= start），這說明我們遇到了一個重復字符。
iii. 為了消除這個重復，我們需要將窗口的左邊界 start 跳躍到重復字符的下一個位置。即 start = map.get(char_end) + 1。
c. 更新 map：無論是否重復，我們都需要更新 char_end 在 map 中的位置為當前的 end 索引。map.put(char_end, end)。
d. 更新 max_len：在每一步之后，當前有效的無重復子串的長度就是 end - start + 1。我們用它來更新 max_len。 max_len = max(max_len, end - start + 1)。
e. end 指針自增，考察下一個字符。
循環結束后，max_len 就是最終答案。
實現代碼

class Solution {
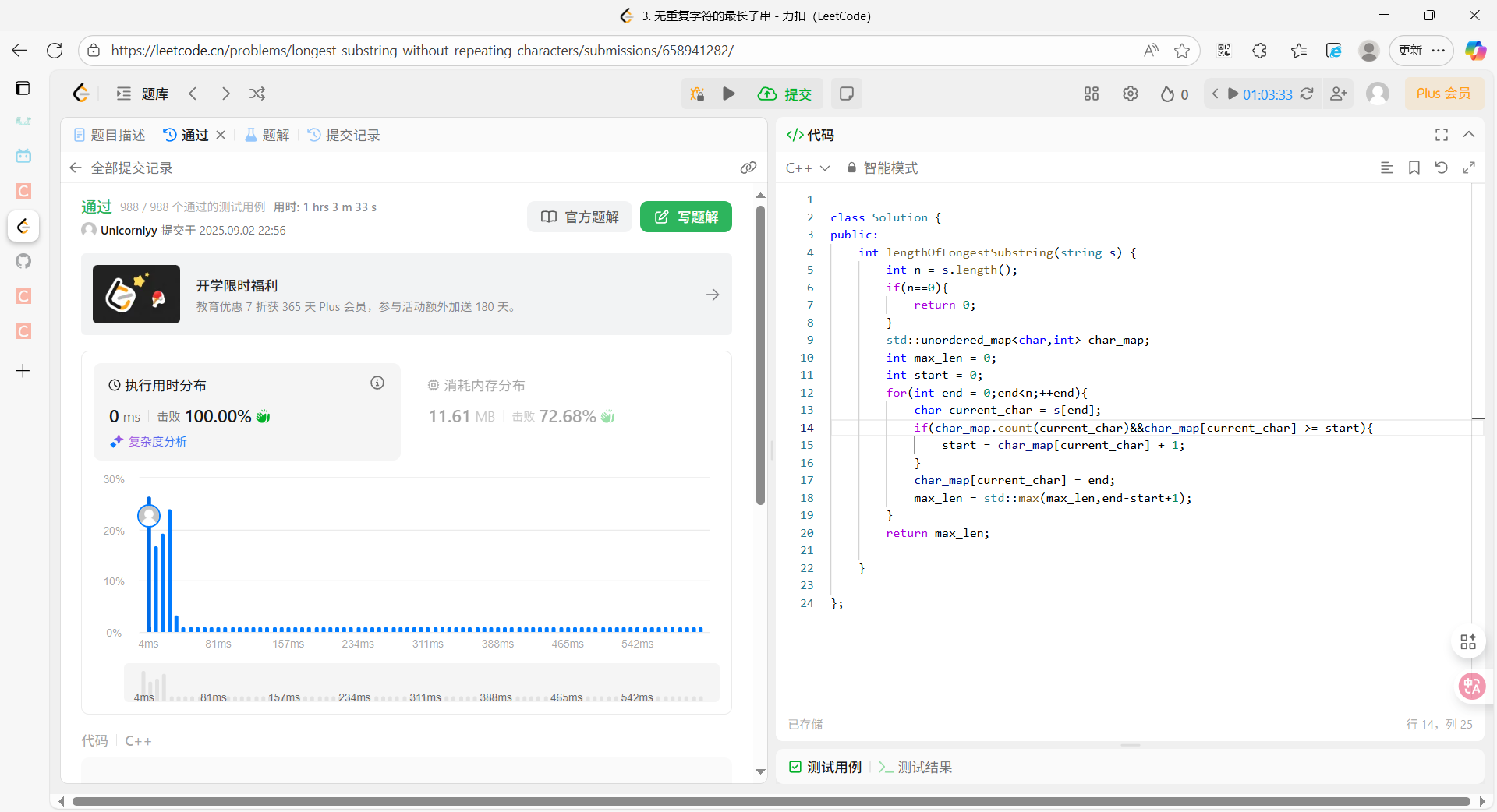
public:int lengthOfLongestSubstring(string s) {int n = s.length();if(n==0){return 0;}std::unordered_map<char,int> char_map;int max_len = 0;int start = 0;for(int end = 0;end<n;++end){char current_char = s[end];if(char_map.count(current_char)&&char_map[current_char] >= start){start = char_map[current_char] + 1;}char_map[current_char] = end;max_len = std::max(max_len,end-start+1);}return max_len;}};

執行結果

復雜度分析
時間：O
空間：O