1.歸并排序

1.1歸并排序概述

歸并排序，其排序的實現思想是先將所有的記錄分開，然后兩兩合并，在合并的過程中將其排好序，最終得到一個完整的序列。由于使用到的遞歸思想，我個人認為也可以叫遞歸排序。歸并排序非常適合大數據排序，大部分數據都在磁盤上，我們可以用歸并排序拆分，我們拆成可以在內存中保存的n個有序區間，往回寫到硬盤里，再進行合并這幾個有序序列的時候工作量就變小了。

1.2歸并排序的執行流程

1.不斷地將當前序列平均分割成兩個子序列：例如下面的序列，被分割成兩個子序列，注意實際寫代碼的時候可能不會完全分割成兩等份

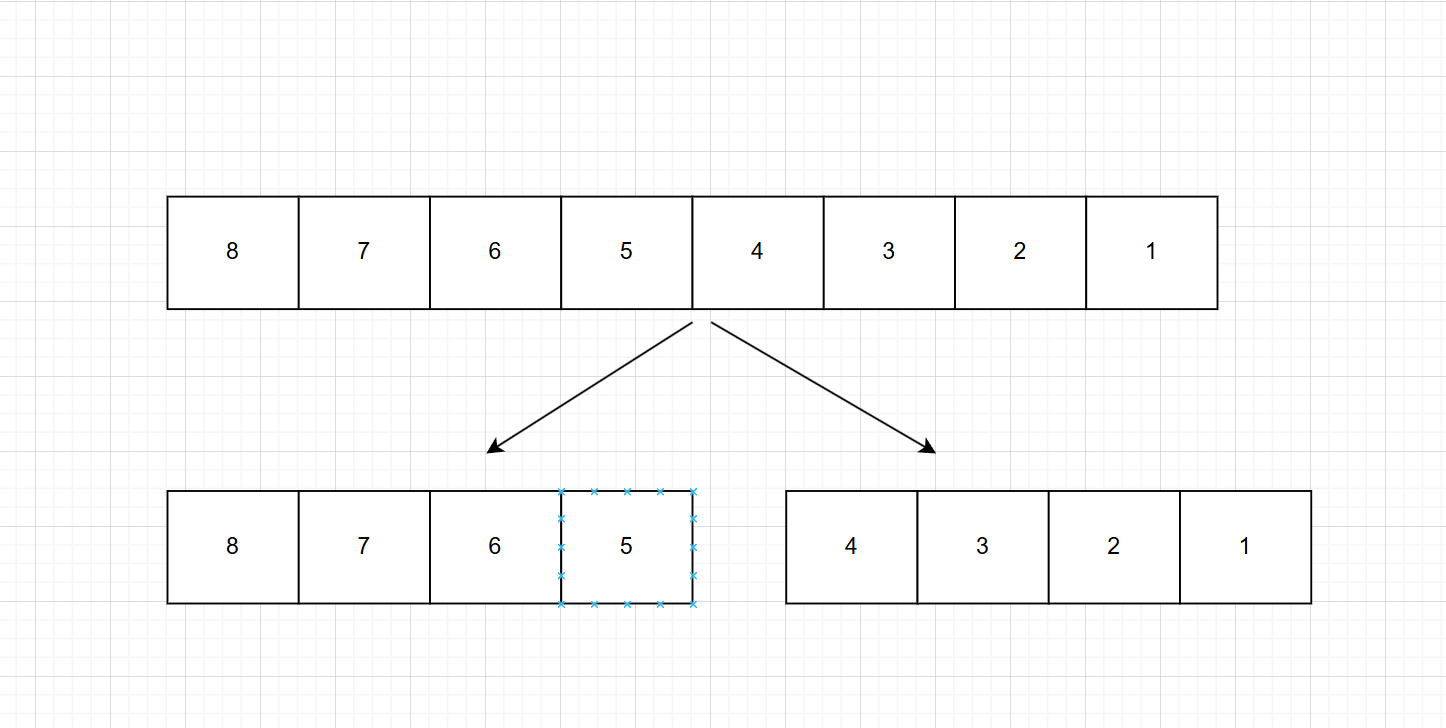
2.然后繼續將這些子序列分割成子序列，直到不能再分割位置。(序列中只剩下一個元素)

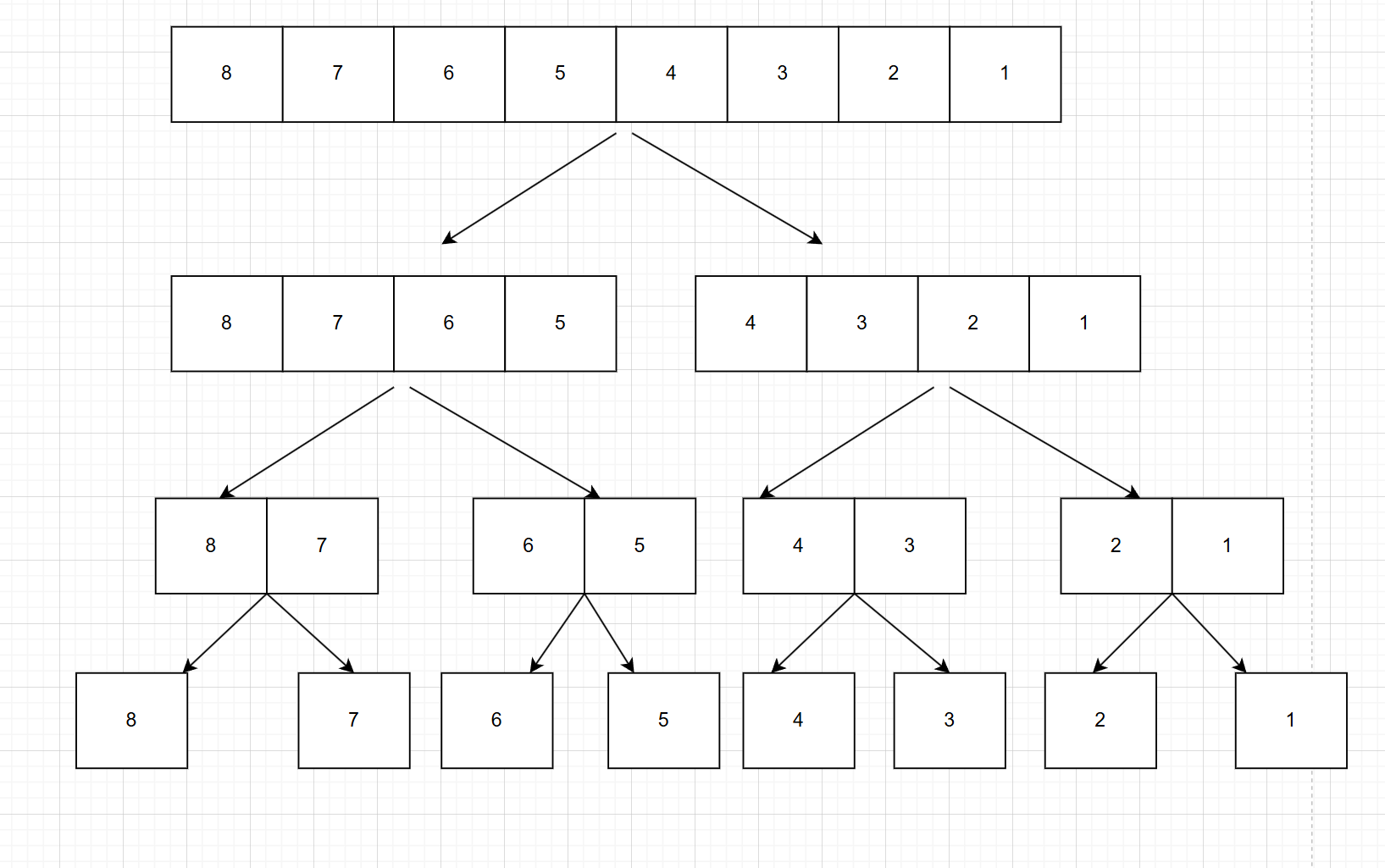
2.接下來，在不斷的將兩個子序列合并成一個有序序列：也就是說，剛剛是拆分，現在是合并。

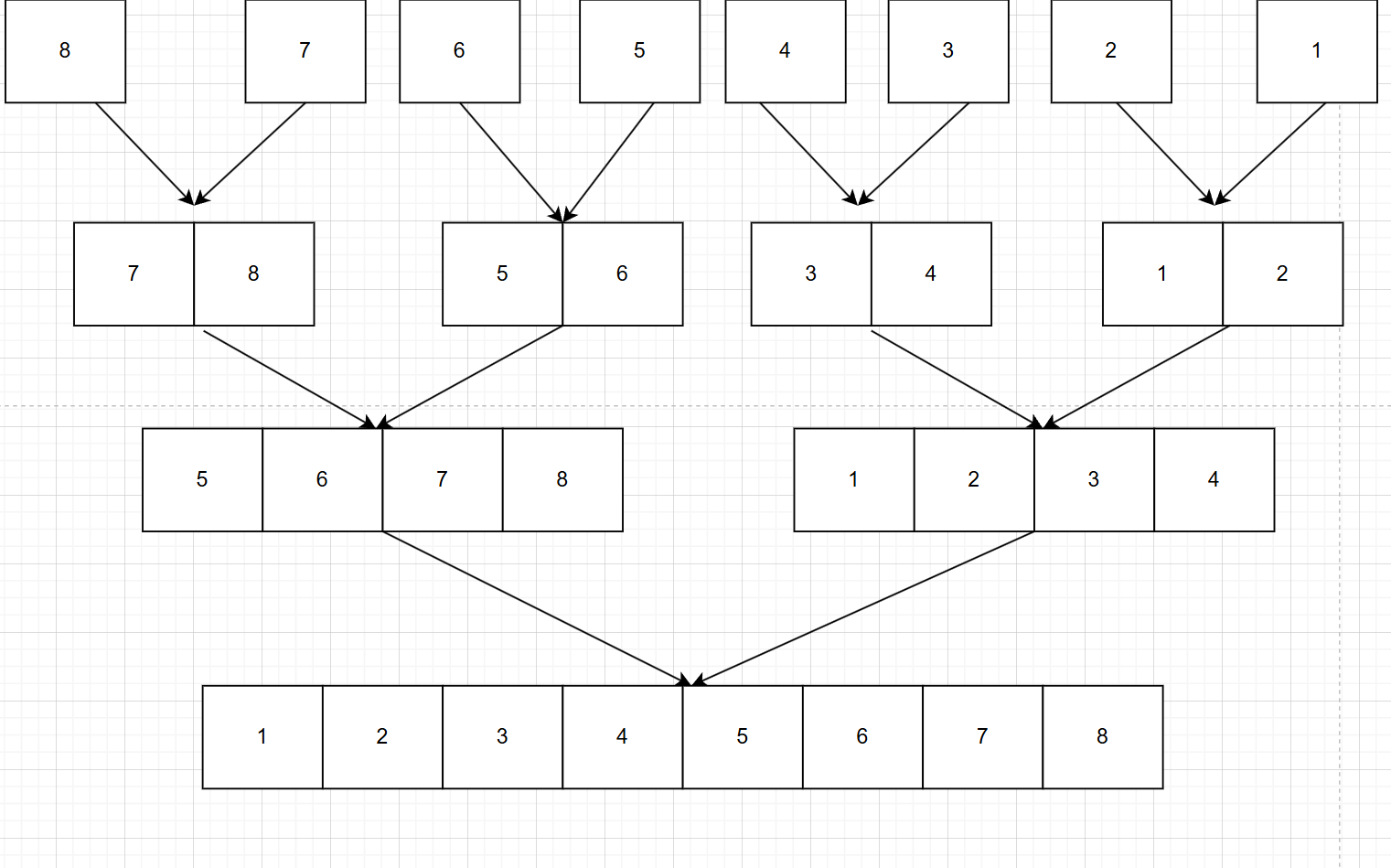
合并的時候比較哪個序列的最小值更小就是真正的最小值，注意合并的7和8和上面分散的7和8是一個空間，我們是在原空間中排好序的，拆分完后我們沿路返回，只是方便大家看流程，在并的過程中我往下面畫的，整個過程和樹的DFS有點像，先處理完一邊，再去處理另一邊。

1.2.1遞(分裂)的過程

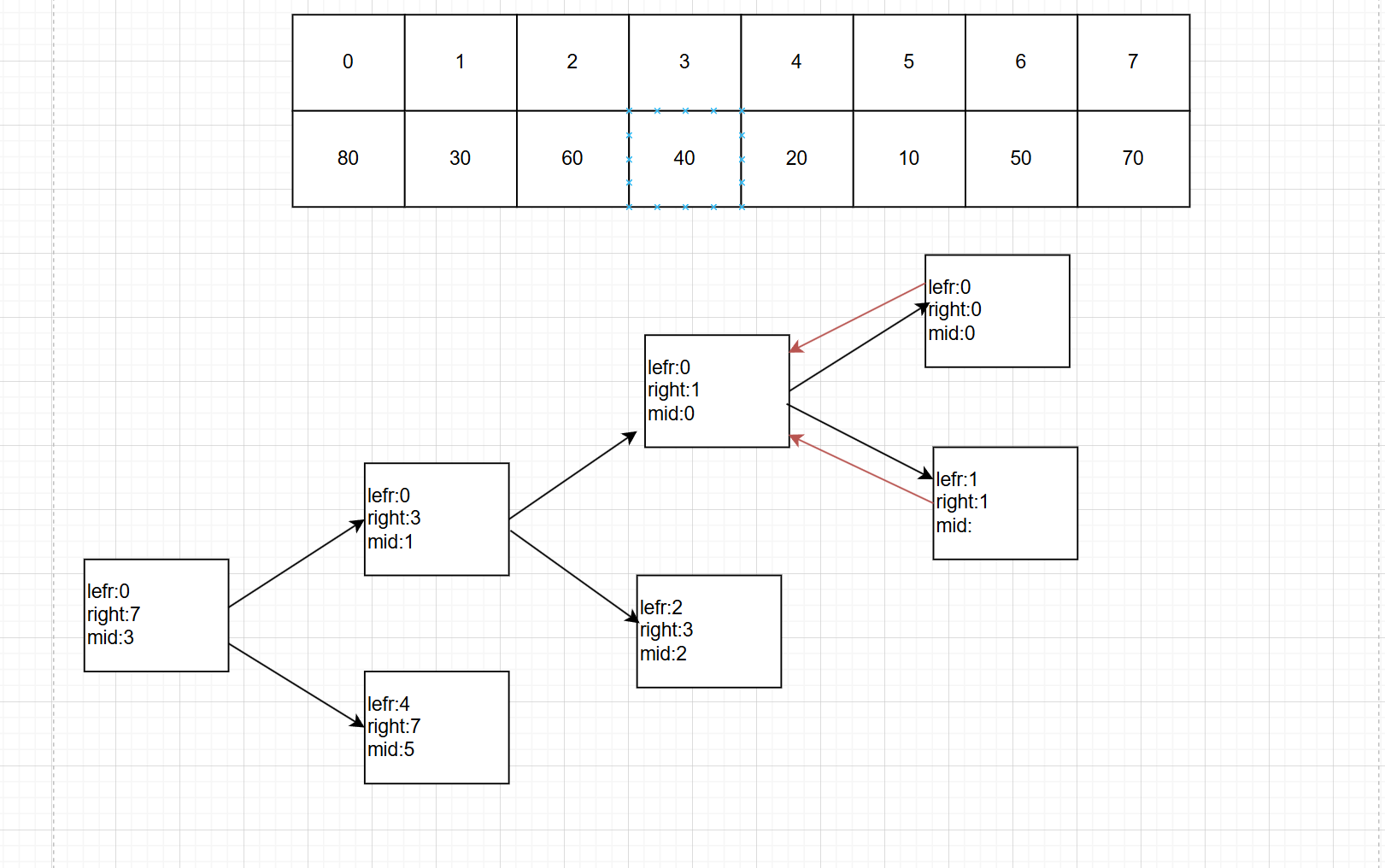
我們設置兩個left和right兩個標志位，不斷地分割序列，直到left==right，說明無法繼續分割了，開始歸回來，圖中我沒有畫完全，只是做個展示。

1.2.2歸(合并)的過程

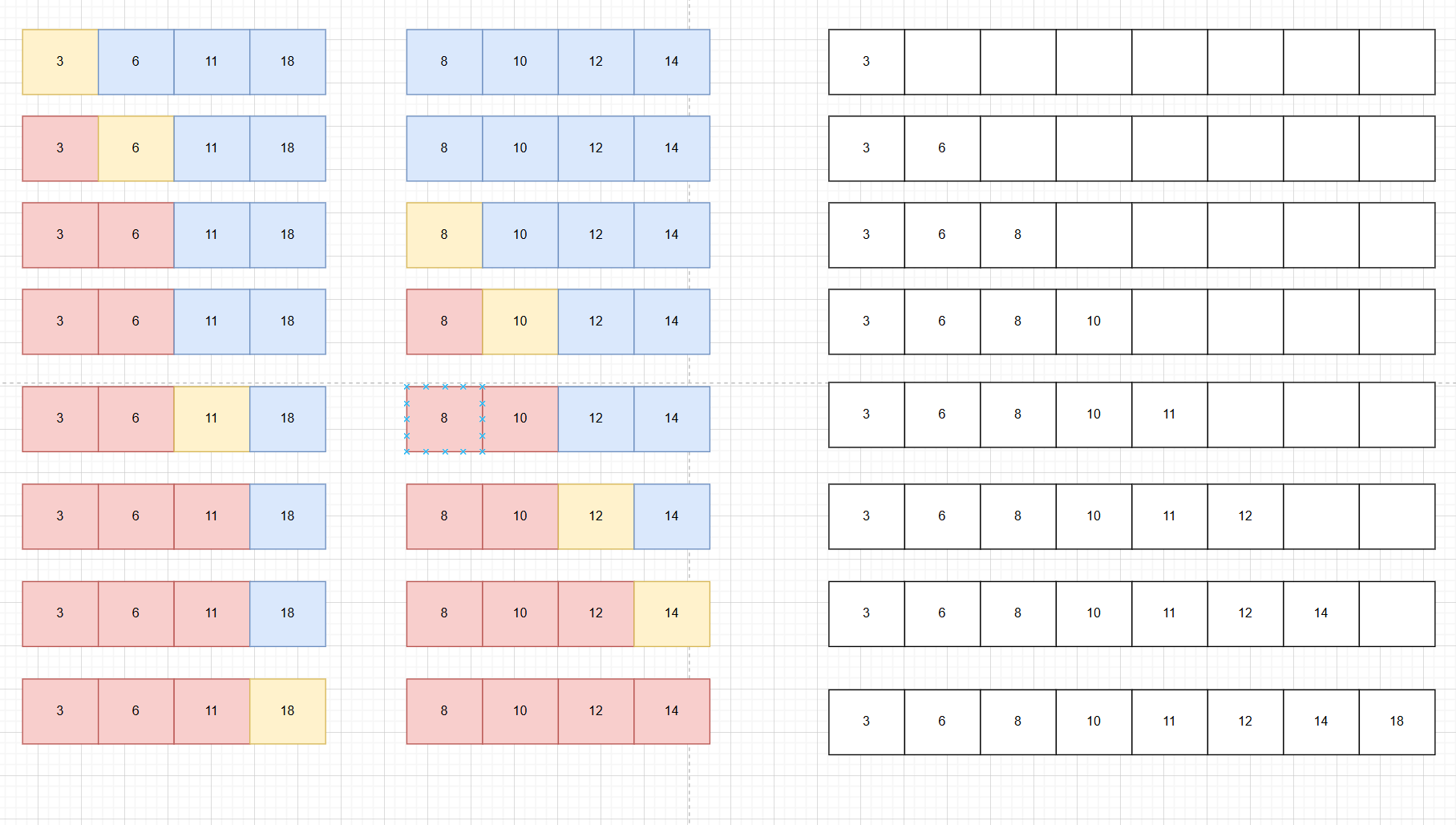
最右邊是我們要排序的序列的原空間，我們創建兩個獨立的空間用來存分裂后的序列，并創建兩個指針指向兩個序列空間中的最小值元素。第一次比較兩個序列中指針指向的更小值為3，把它放入原序列的空間的第一號元素，在哪個空間中放的序列我們就把哪個空間的最小值指針往右邊移動一位，另一個空間中的最小值元素指針不動，然后再次比較兩個空間中指針指向的元素的較小值依次類推直到把其中某一個空間中的值全部放入了原空間中，再把另一個空間中的所有值排在后面即可。

1.3歸并排序的代碼實現

遞進去拆分：

// 遞歸的分解table[left, right]區間
static void merge_loop(SortTable *table, int left, int right) {if (left >= right) {return;}int mid = (left + right) / 2;merge_loop(table, left, mid);merge_loop(table, mid + 1, right);// 區間拆分結束，合并兩個子區間merge(table, left, mid, right);
}

合并過程：

// merge合并過程
static void merge(SortTable *table, int left, int mid, int right) {int n1 = mid - left + 1;        // 左邊區間的個數int n2 = right - mid;           // 右邊區間的個數// 分配aux1和aux2，將已經有序的左區間和已經有序的右區間 初始化臨時區域Element *aux1 = malloc(sizeof(Element) * n1);if (aux1 == NULL) {return;}Element *aux2 = malloc(sizeof(Element) * n2);if (aux2 == NULL) {free(aux1);return;}for (int i = 0; i < n1; i++) {aux1[i] = table->data[left + i];}for (int i = 0; i < n2; ++i) {aux2[i] = table->data[mid + 1 + i];}// 將臨時的有序空間aux1和aux2進行歸并int i = 0;          // 標記aux1區間待查找的位置int j = 0;          // 標記aux2區間待查找的位置int k = left;       // 標記原空間存放結果的區域位置while (i < n1 && j < n2) {if (aux1[i].key <= aux2[j].key) {table->data[k] = aux1[i];++i;} else if (aux1[i].key > aux2[j].key) {table->data[k] = aux2[j];++j;}k++;}// 判斷究竟是aux1還是aux2區域遍歷結束while (i < n1) {table->data[k++] = aux1[i++];}while (j < n2) {table->data[k++] = aux2[j++];}free(aux1);free(aux2);
}

注意這里初始化的時候要加上序列左邊的基地址。

接口調用：

/* 歸并排序：從上往下，從下往上兩個過程* 從上往下的過程：*  a. 分解 -- 將當前區間一分為二*  b. 求解 -- 遞歸對兩個子區間a[low...mid] 和 a[mid+1...high]進行歸并排序*/
void mergeSort(SortTable *table) {merge_loop(table, 0, table->length - 1);
}

最后來測一下：

#include "mergeSort.h"int main() {int n = 10000;SortTable *table = generateRandomArray(n, 0, n + 5000);testSort("Merge Sort", mergeSort, table);releaseSortTable(table);return 0;
}

結果：

D:\work\DataStruct\cmake-build-debug\04_Sort\MergeSort.exe
Merge Sort cost time: 0.002000s.進程已結束，退出代碼為 0

時間復雜度也是接近O(nlogn)。

2.計數排序

計數排序（Counting Sort）是一種針對于特定范圍之間的整數進行排序的算法。它通過統計給定數組中不同元素的數量（類似于哈希映射），然后對映射后的數組進行排序輸出即可。（計數排序在某些情況下比快速排序還要快）

2.1算法思想

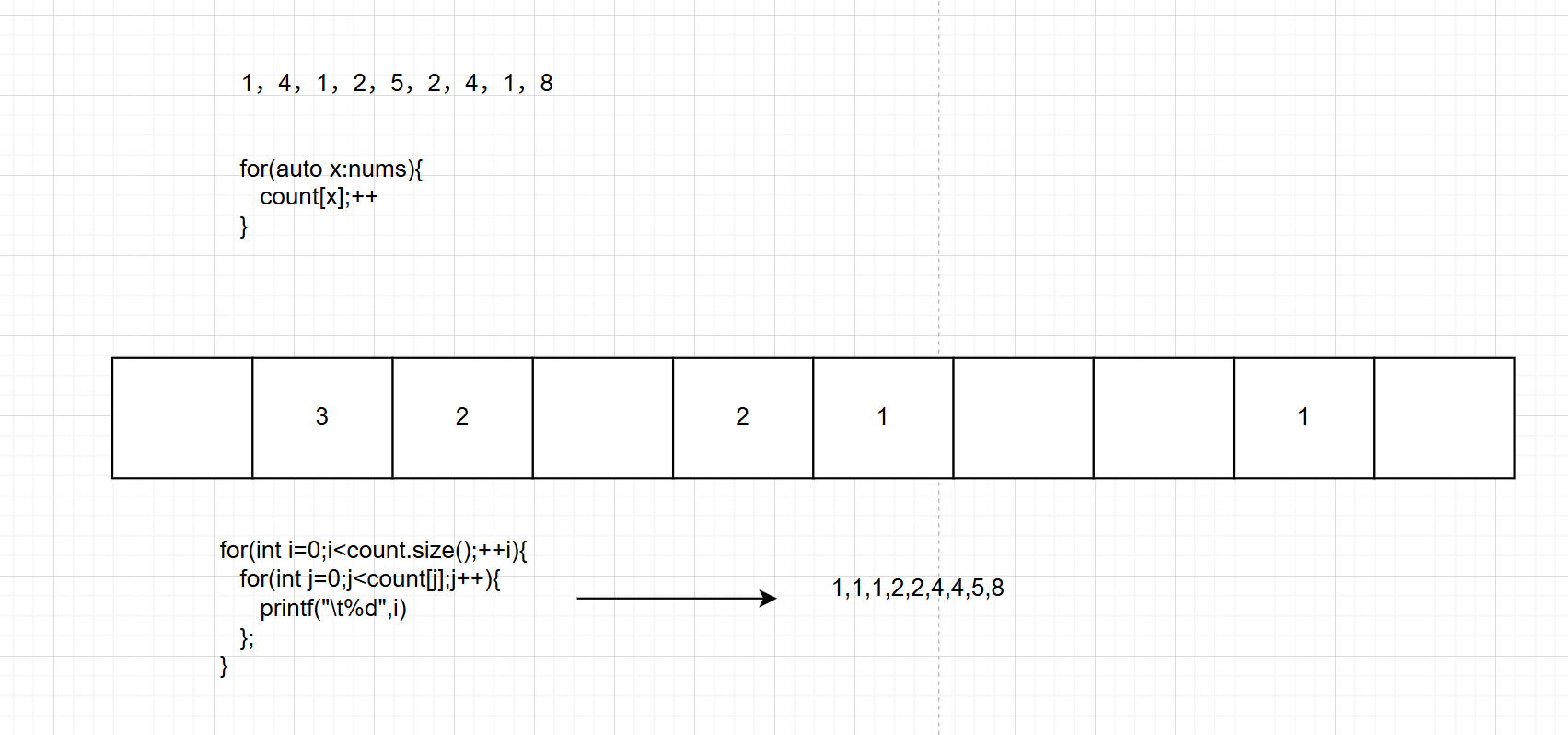
我們以數組 [1,4,1,2,5,2,4,1,8] 為例進行說明。

第一步：建立一個初始化為 0 ，?度為 9 (原始數組中的最大值 8 加 1) 的數組 count[]

第二步：遍歷數組[1,4,1,2,5,2,4,1,8]，訪問第一個元素1，然后將數組標為1的元素加1，表示當前1出現了1此，即count[1]=1;

依次遍歷，對count進行統計。

2.2計數排序的改進

• 無法對負數進行排序
• 極其浪費空間
• 是一個不穩定排序

2.2.1優化1

只要不再以數列的[最大值+1]作為統計數組的長度，而是以數列[最大值-最小值+1]作為統計數組的長度即可。數列最小值作為一個偏移量，用于計算整數在統計數組中的下表

2.2.2優化2

為了使計數排序穩定，我們從統計數組的第2個元素開始，每一個元素都加上前面元素之和，相加的目的是讓統計數組存儲的元素值，等于對應整數的最終排序位置的序號，遍歷的時候從后向前遍歷原數組（在填充輸出數組時）來保證穩定性。

計數排序了解一下即可，還有一些排序比如選擇排序，桶排序我就不一一寫了，大家可以自己去看，大概先寫這些吧，今天的博客就先寫到這，謝謝您的觀看。