什么是MoE?

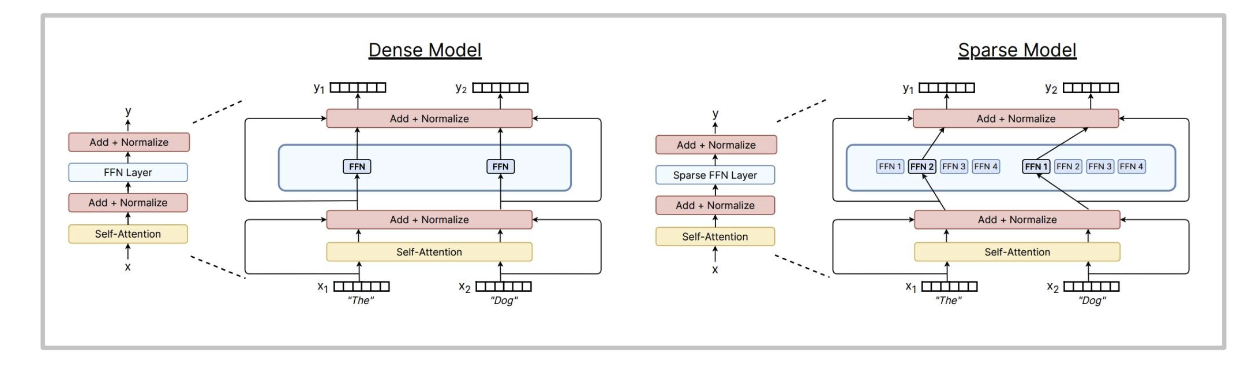
用（多個）大型前饋網絡和一個選擇器層取代大型前饋網絡。你可以在不影響浮點運算次數的情況下增加專家數量。

MoE受歡迎的原因

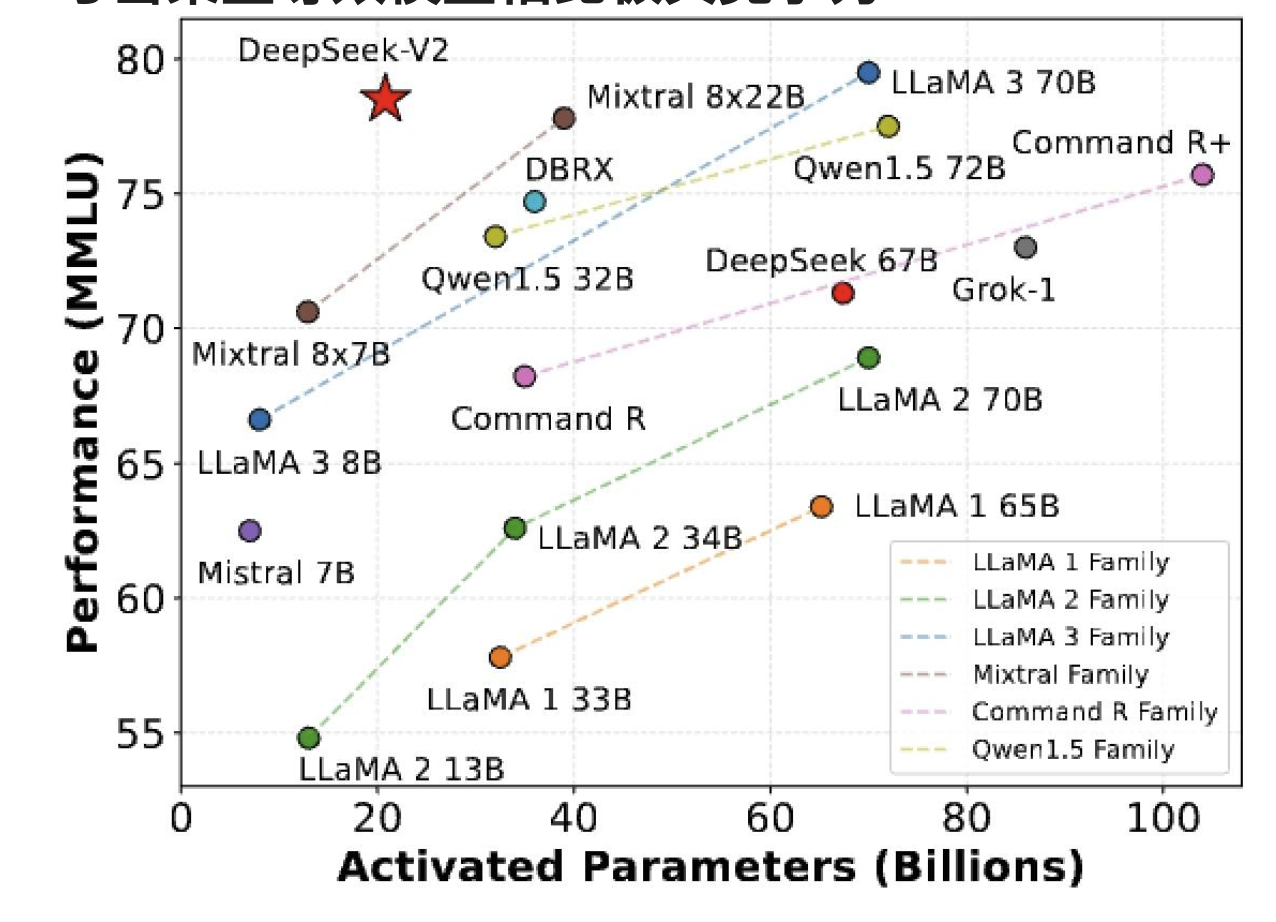
相同的浮點運算次數，更多的參數表現更好

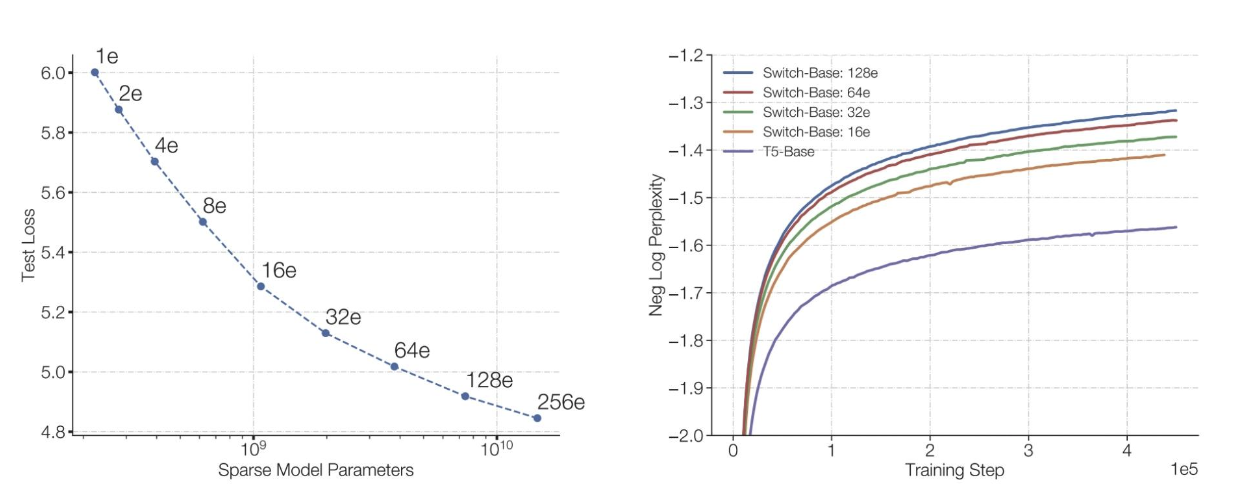
訓練混合專家模型（MoEs）速度更快

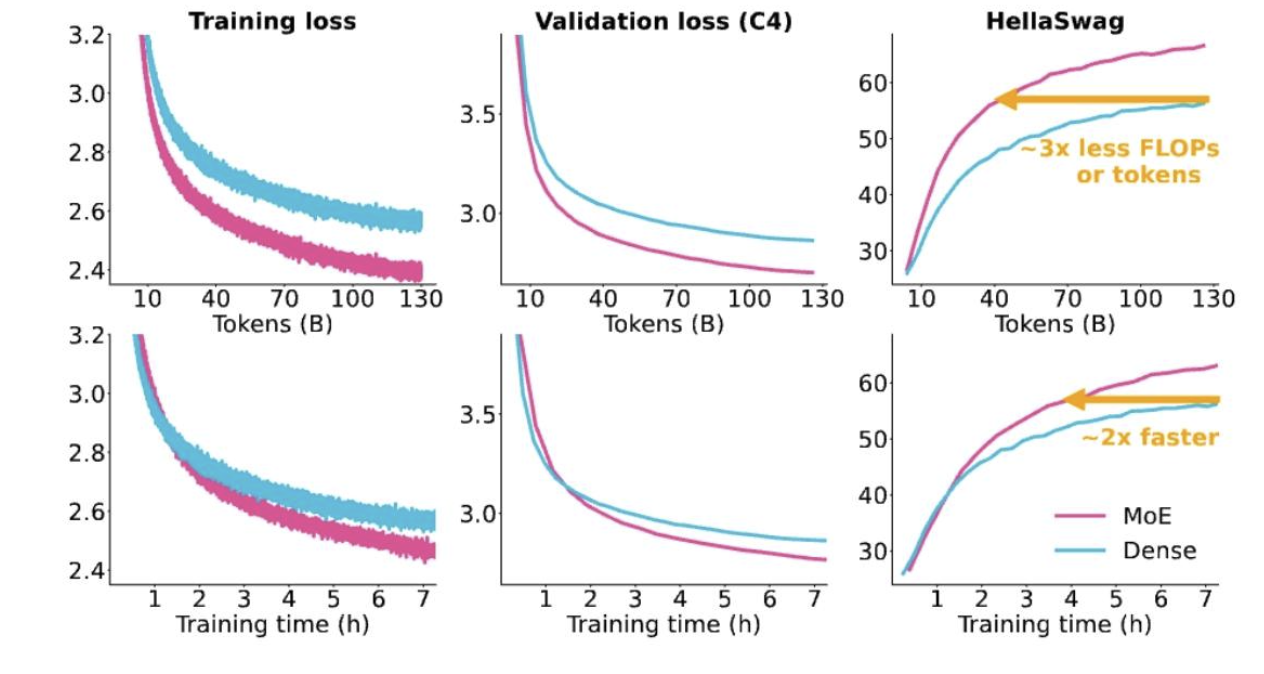
訓練混合專家模型（MoEs）速度更快

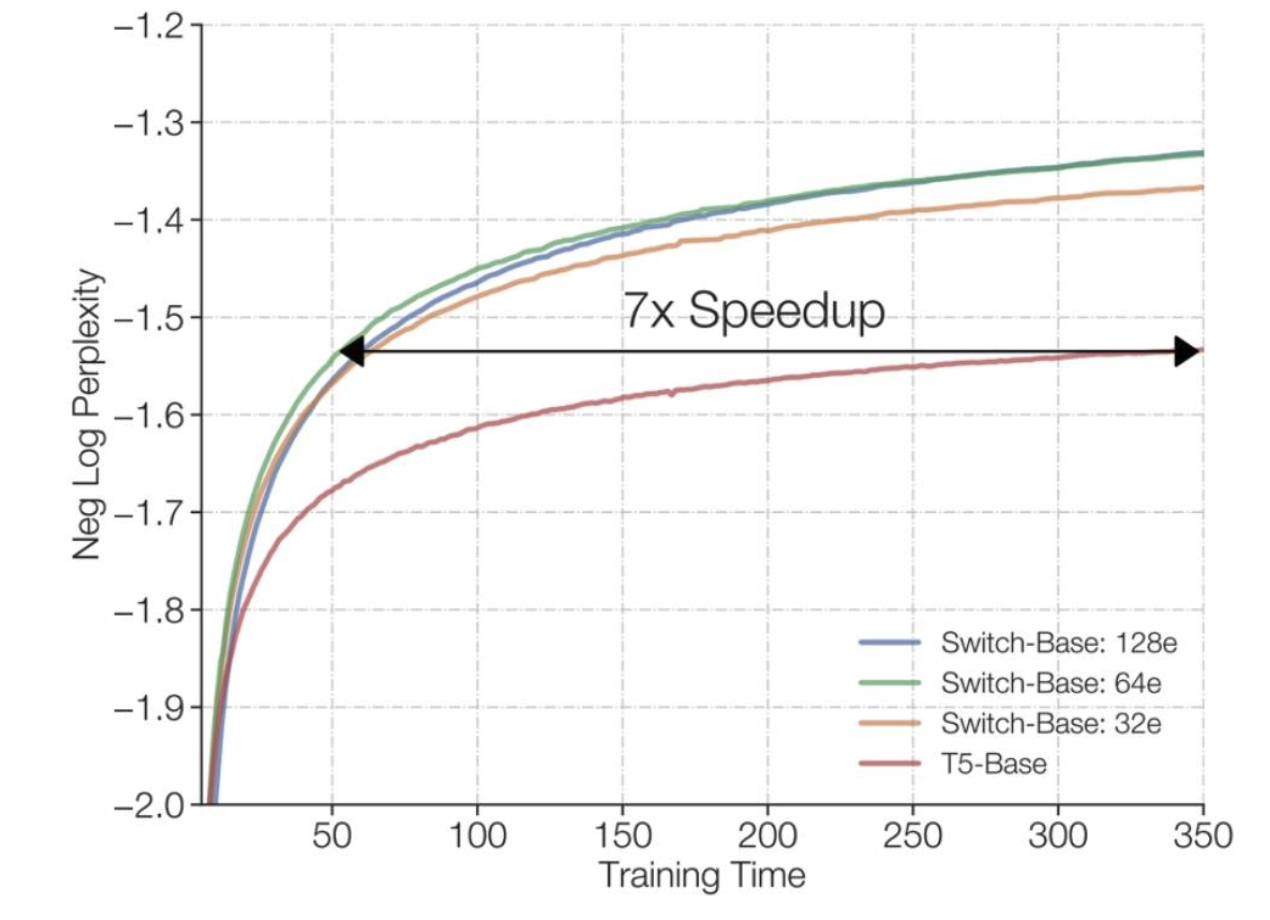
與密集型等效模型相比極具競爭力

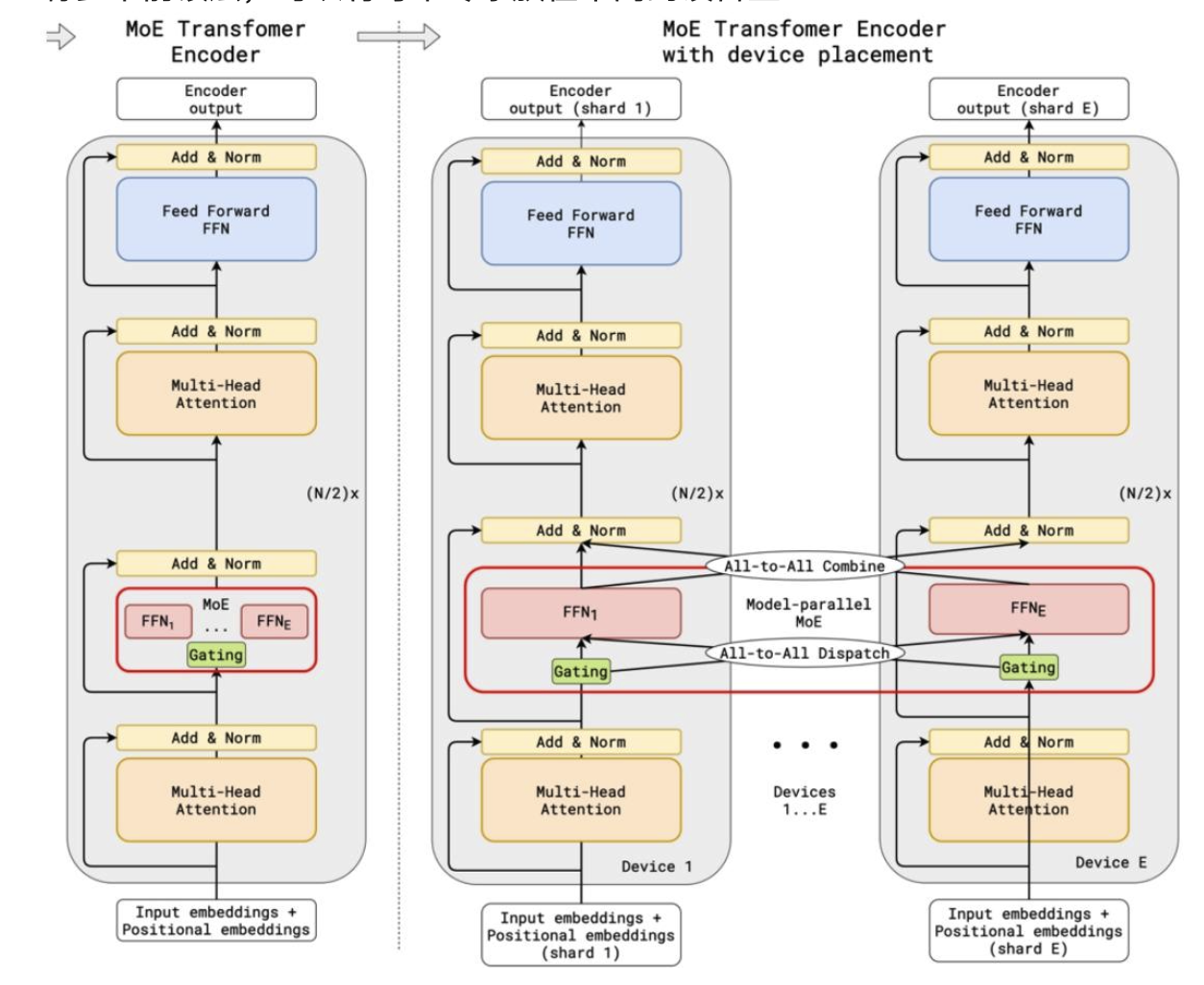
可并行到多個設備（專家并行性）

有多個前饋層，可以將每個專家放在不同的設備上

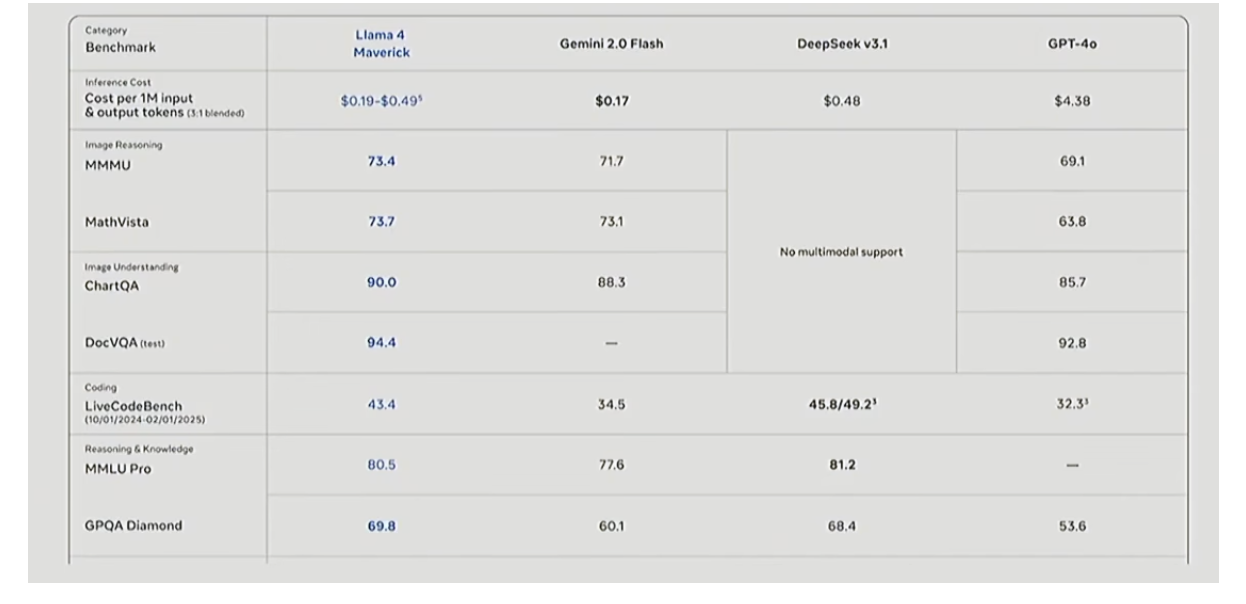
一些混合專家（MoE）的成果——來自西方

混合專家模型（MoE）大多是性能最高的開源模型，而且速度相當快

中國團隊早期的混合專家（MoE）成果——通義千問

中國的大語言模型公司也在較小規模上做了不少混合專家（MoE）相關工作。

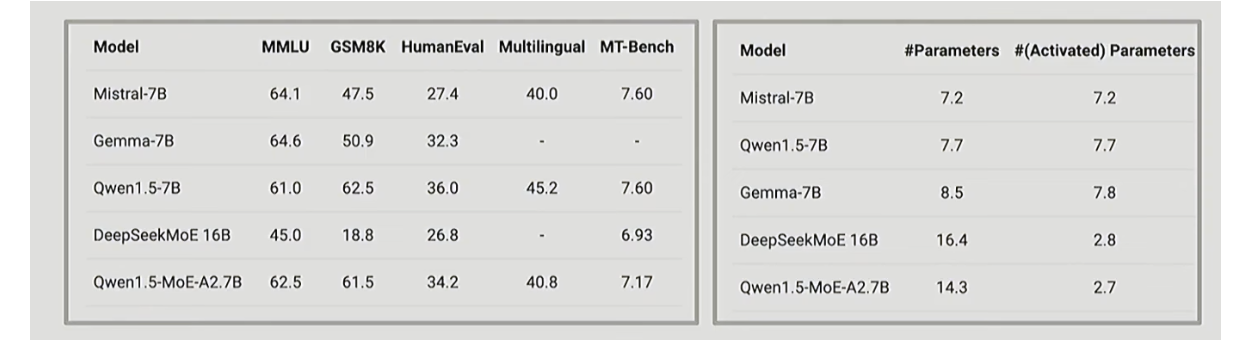
中國團隊早期的混合專家模型（MoE）成果

最近也有一些關于混合專家模型（MoE）的不錯的消融實驗研究，表明它們總體表現良好。

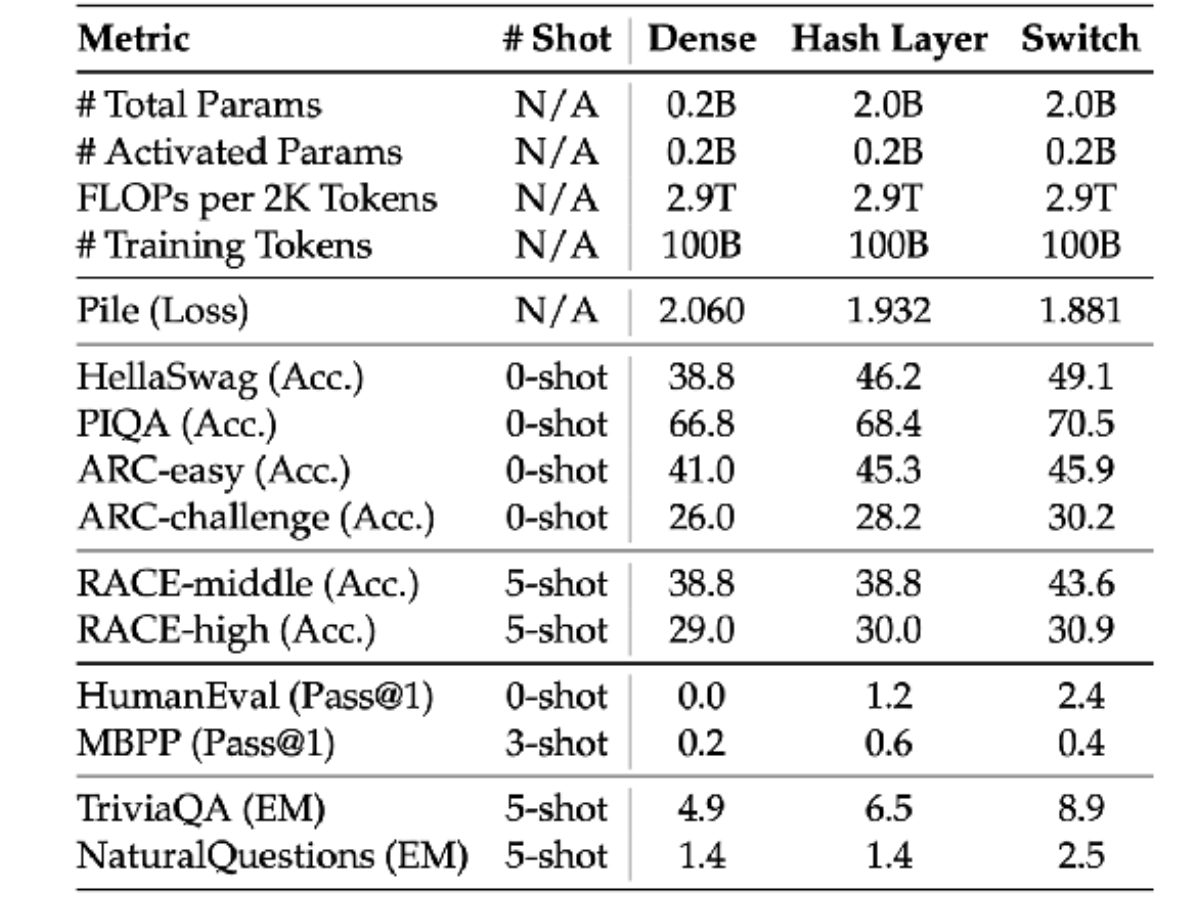
近期混合專家（MoE）結果 – DeepSeek v3

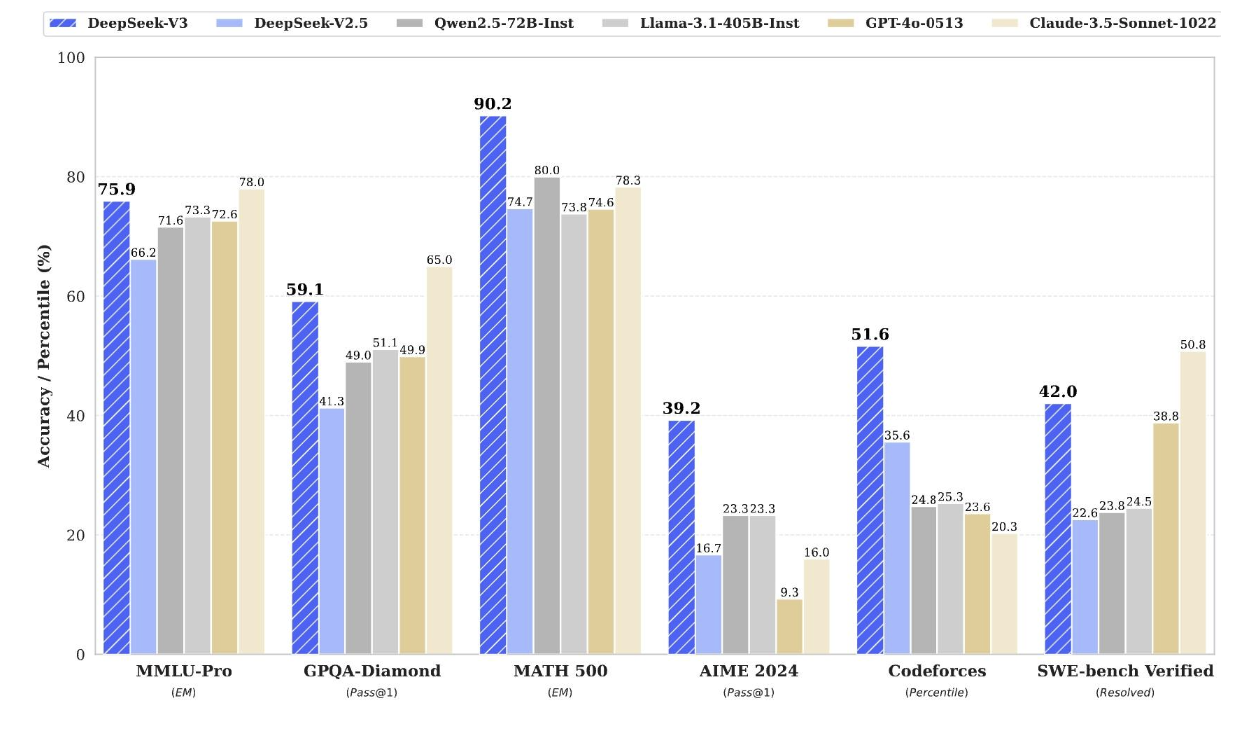
為什么混合專家模型（MoEs）沒有更受歡迎呢？

基礎設施復雜 / 多節點優勢
訓練目標在一定程度上是啟發式的（且有時不穩定）

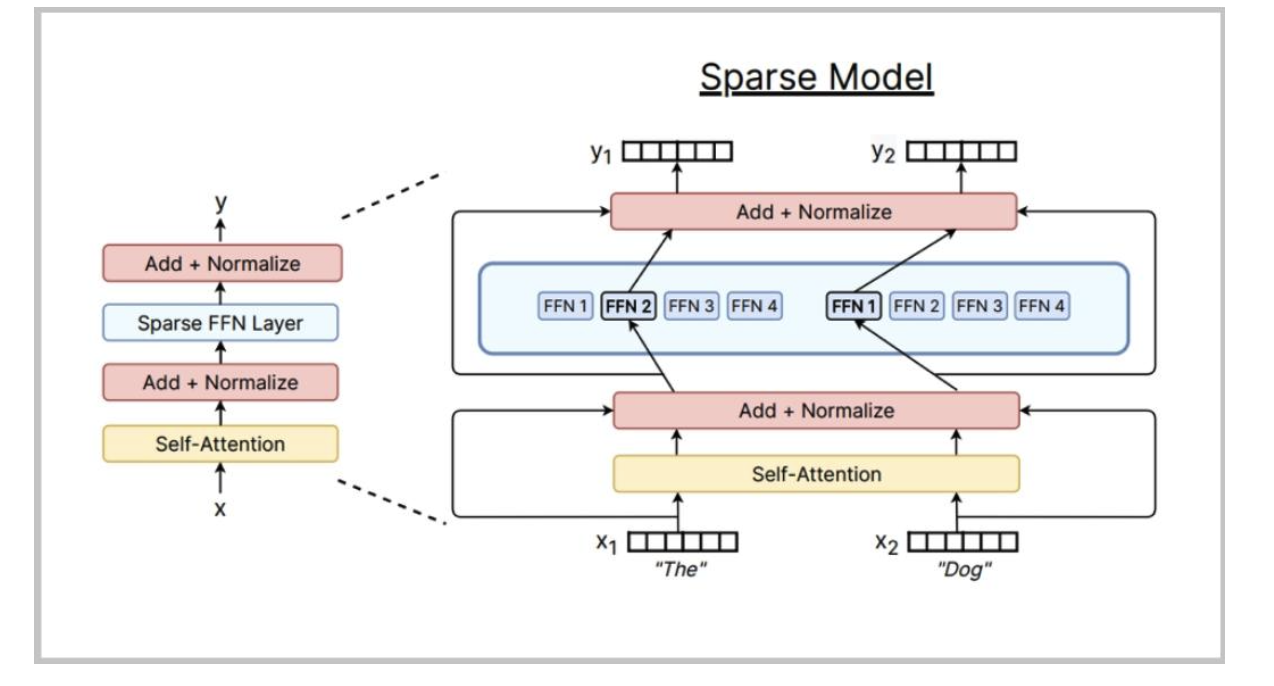
混合專家模型（MoE）通常是什么樣子

典型做法：將多層感知器（MLP）替換為專家混合（MoE）層

不太常見的做法：將MoE用于注意力頭（不穩定）

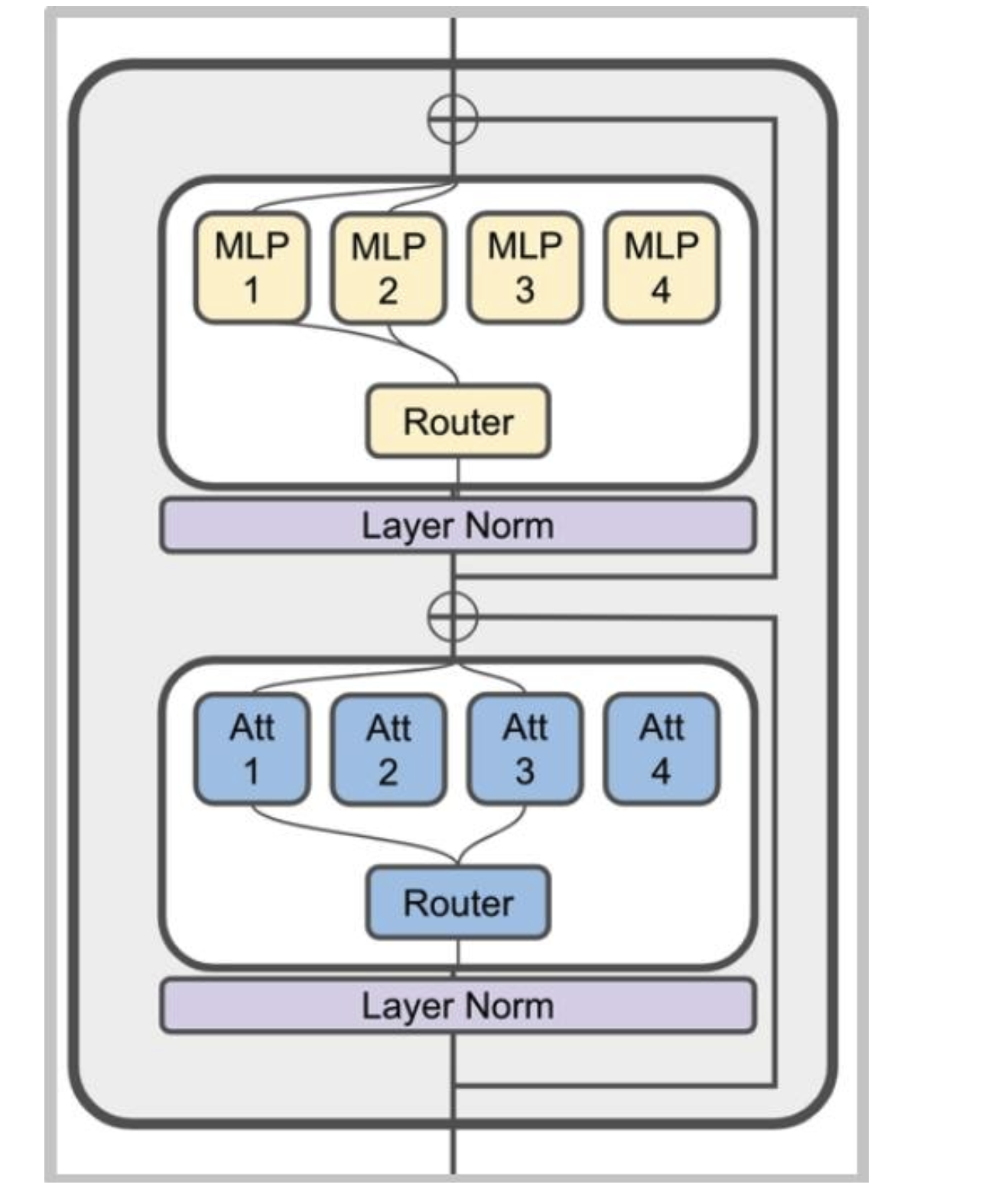
MoE的變種

路由函數
專家規模
訓練目標

路由功能

概述

許多路由算法歸根結底都是“選擇前 k 個”

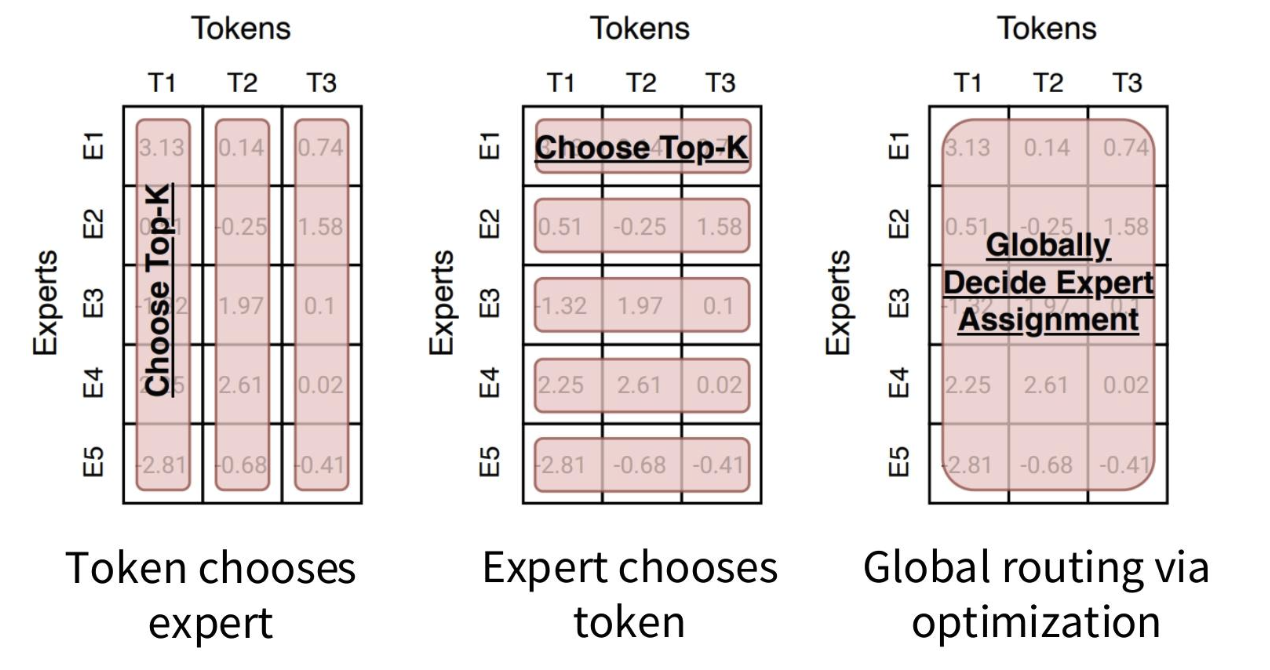
路由類型

幾乎所有的混合專家模型（MoE）都采用標準的“令牌選擇前 k 個”路由方式。最近的一些消融實驗

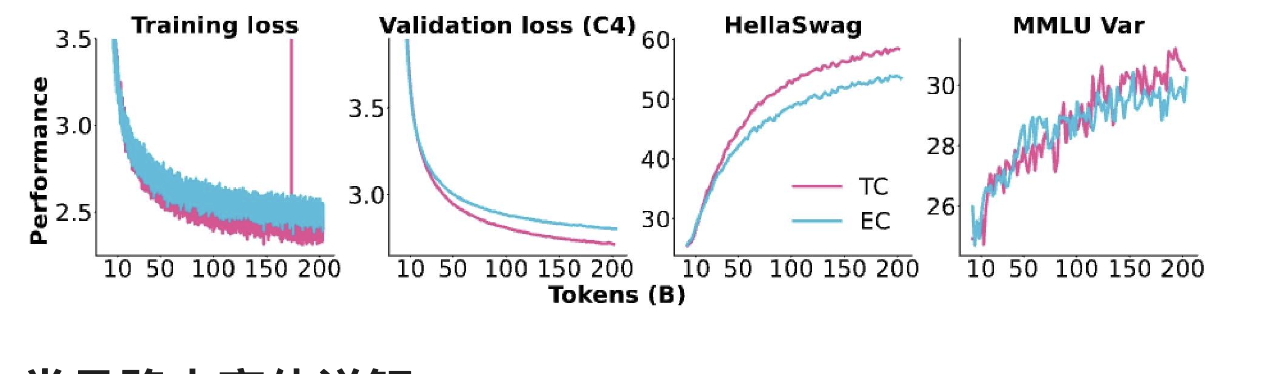
常見路由變體詳解

Top-k

殘差流輸入x
x將進入路由器中，路由器類似于注意力操作(存在線性內積+softmax)
然后選出活躍度最高的前 K 名專家,并對這些輸出進行門控
根據具體情況,可能會根據此路由器權重對輸出進行加權,然后，將只輸出加權平均值或綜合

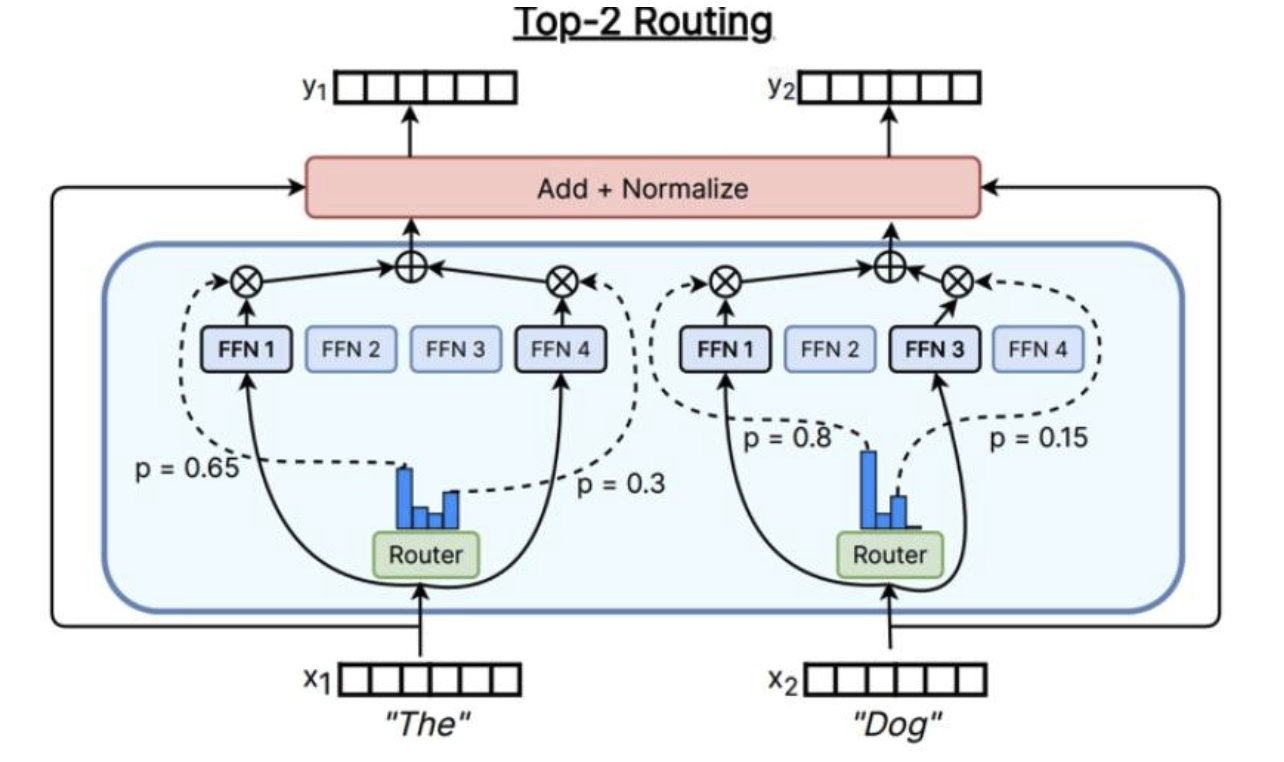
用于大多數混合專家模型（MoE）
Switch Transformer(k=1)
Gshard ((k=2)) 、Grok（2個）、Mixtral（2個）、通義千問（4個）、DBRX（4個）

Hashing

只需要使用哈希函數，就可以將x映射到專家上，即使沒有處理語義信息，依舊可以從基于散列的MoE中得到收益

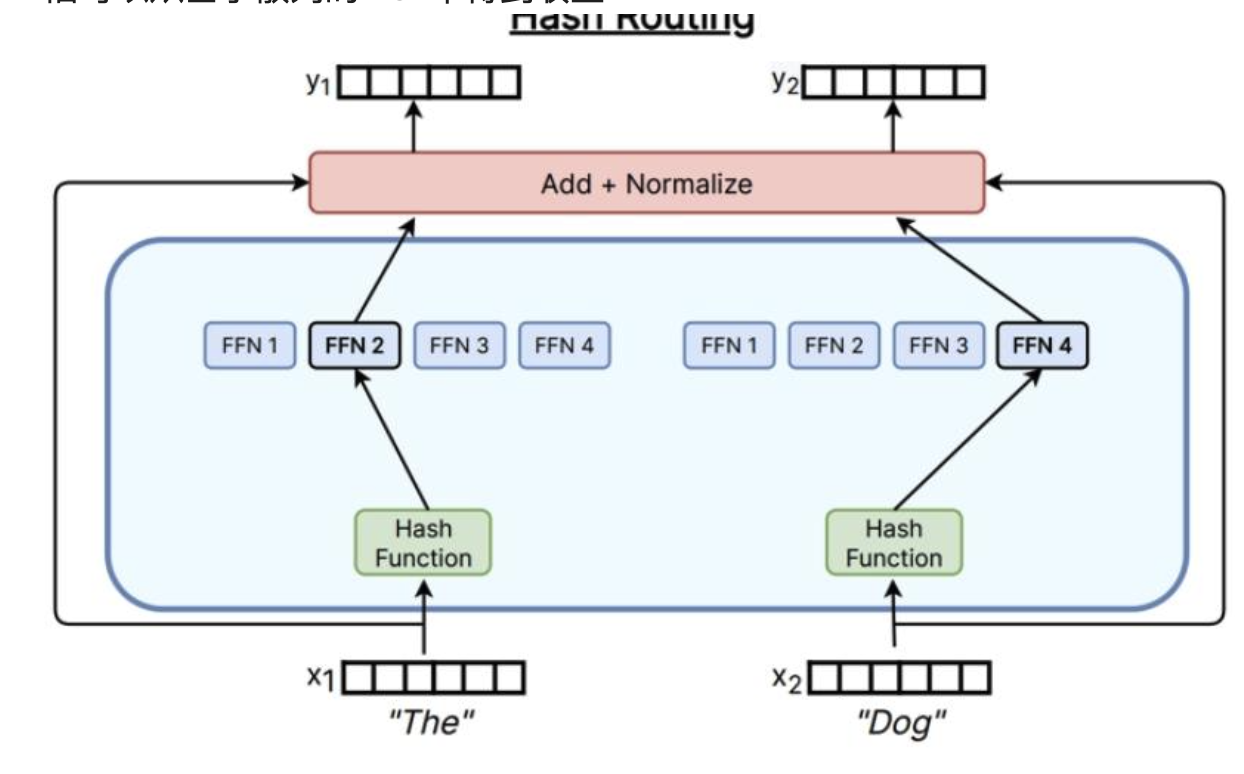
其他路由方法

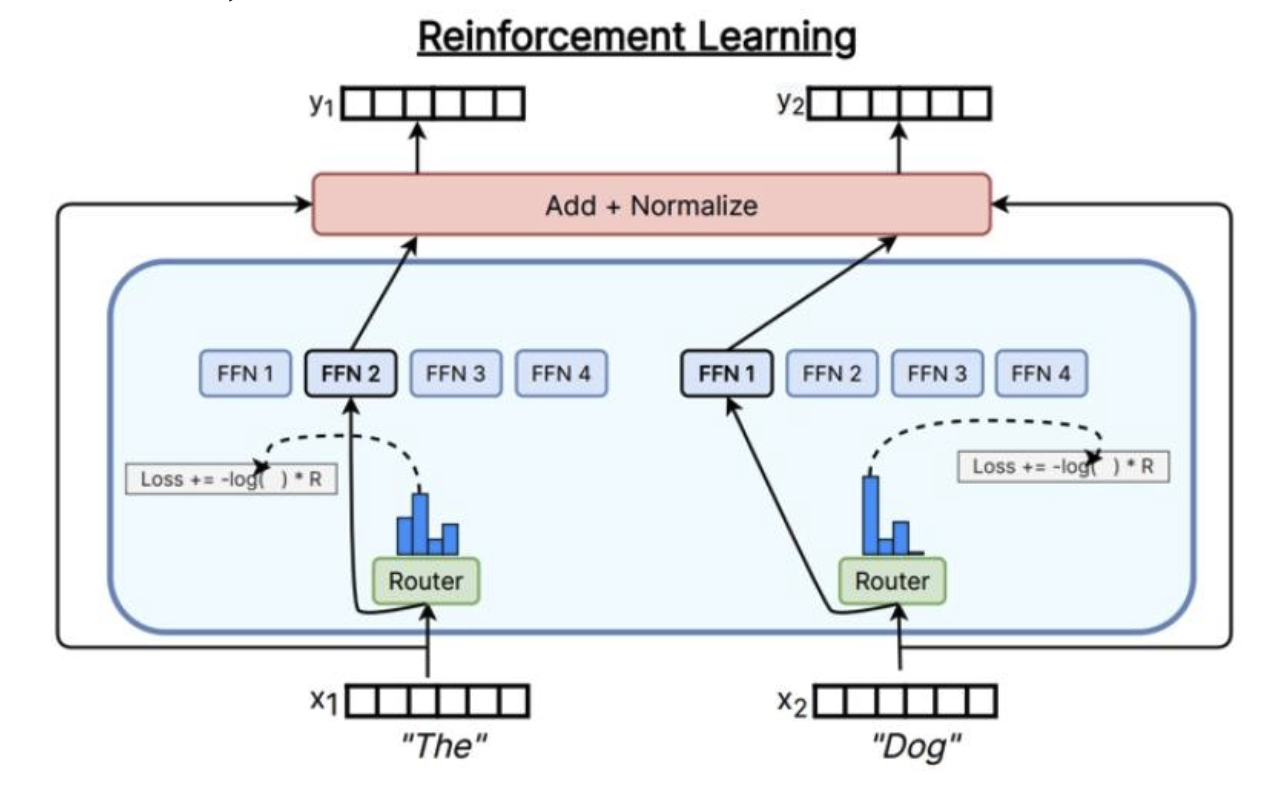
通過強化學習學習路由

計算成本高，大于好處

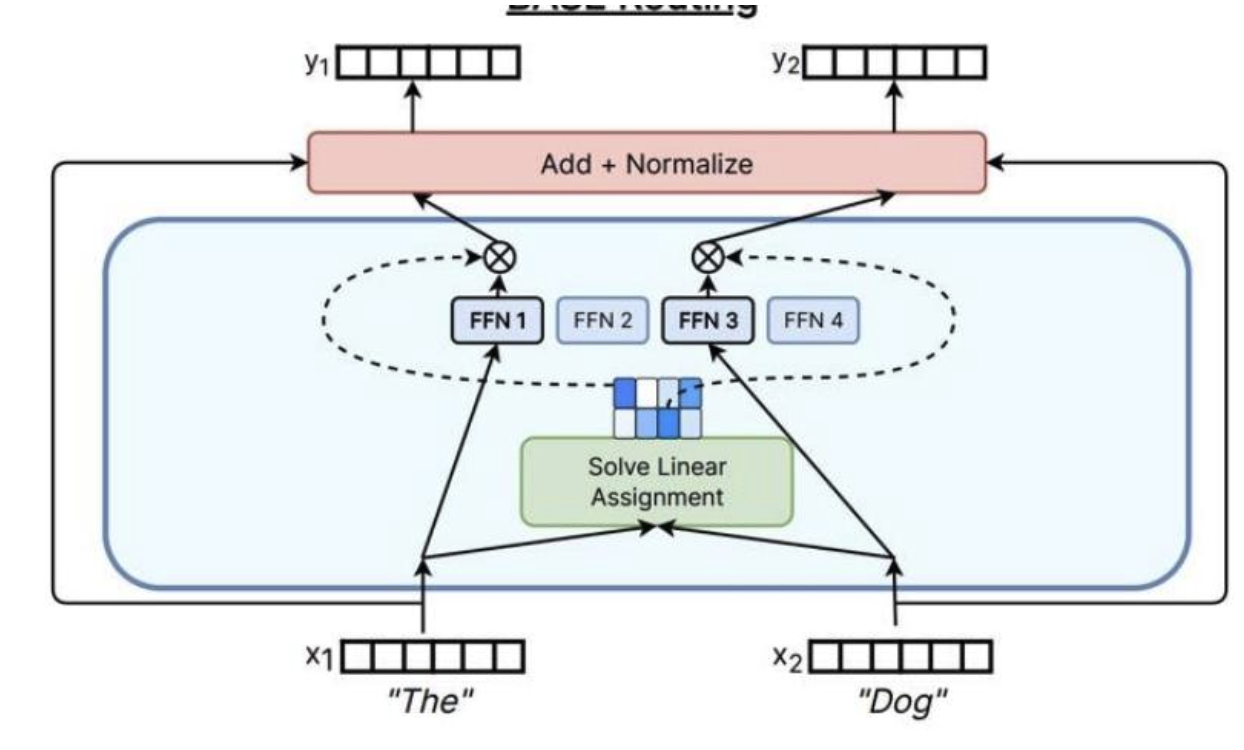
解決一個匹配問題

Top-K路由詳解

1. 計算專家權重（(s_{i,t})）：對于第l層的輸入特征$(u_t^l)$，通過與專家i的門控向量($e_i^l$)進行內積運算，再經過 Softmax 函數歸一化，得到該輸入分配給專家i的權重($s_{i,t}$)，即($s_{i,t}=Softma{x}_i\left(u_t^{l^T}{e}_i^l\right)$)。

2. 篩選 Top-k 專家（(KaTeX parse error: Expected '}', got 'EOF' at end of input: g_{i,t})）：從所有專家的權重($s_{i,t}$)中選取數值最高的前k個，對于這k個專家，保留其權重作為門控系數($g_{i,t}$)；而其他未被選中的專家，門控系數設為 0，即(gi,t={si,t,si,t∈Topk({sj,t∣1≤j≤N},K),0,otherwise,g_{i, t}= \begin{cases}s_{i, t}, & s_{i, t} \in Topk\left(\left\{s_{j, t} | 1 \leq j \leq N\right\}, K\right), \\ 0, & otherwise, \end{cases}gi,t?={si,t?,0,?si,t?∈Topk({sj,t?∣1≤j≤N},K),otherwise,?)。

3. 計算輸出特征（($h_t^l$)）：將篩選出的 Top-k 專家對輸入特征($u_t^l$)的處理結果（即($FF{N}_i\left(u_t^l\right)$)）與各自的門控系數($g_{i,t}$)相乘后求和，再加上原始輸入特征($u_t^l$)，得到該層的輸出特征($h_t^l$)，即($h_t^l={\sum }_{i=1}^N\left(g_{i,t}FF{N}_i\left(u_t^l\right)\right)+u_t^l$)。
   如果這里只使用softmax而不是用TOP-k,那么就失去了模型本身的意義，使得每次都會激活所有模型，違背了我們在訓練和推理中都有少量稀疏的活躍模型的目的

近期由DeepSeek和其他中國大語言模型帶來的變化

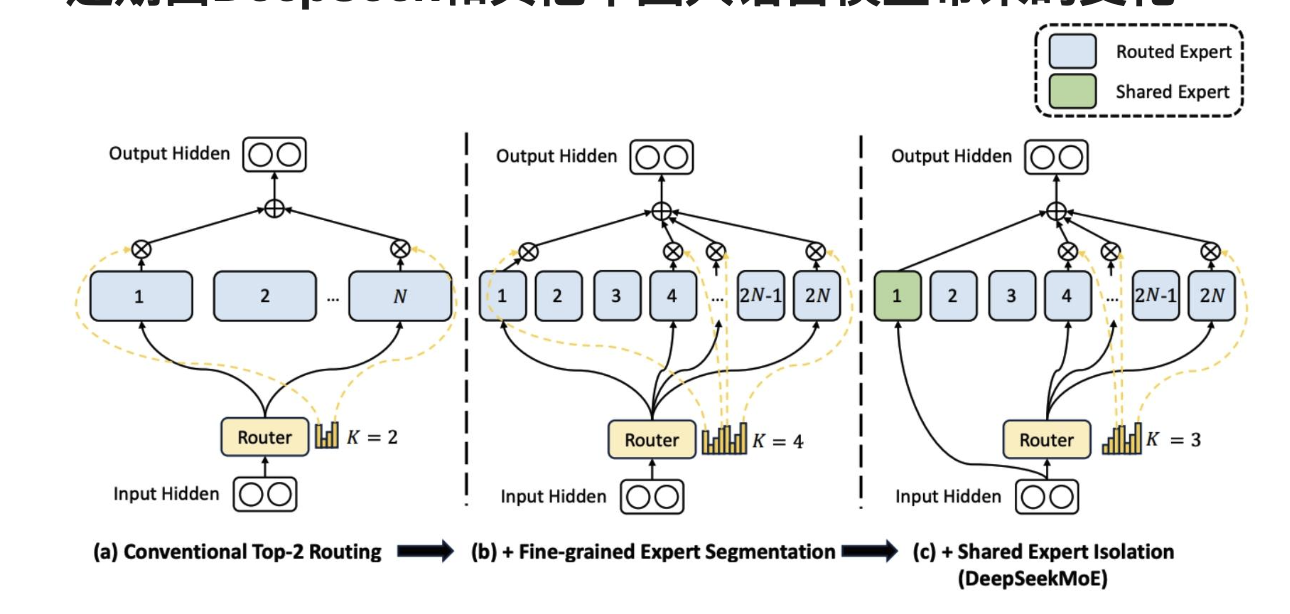
規模較小、數量較多的專家 + 一些始終在線的共享專家。

DeepSeek論文中的各種消融實驗

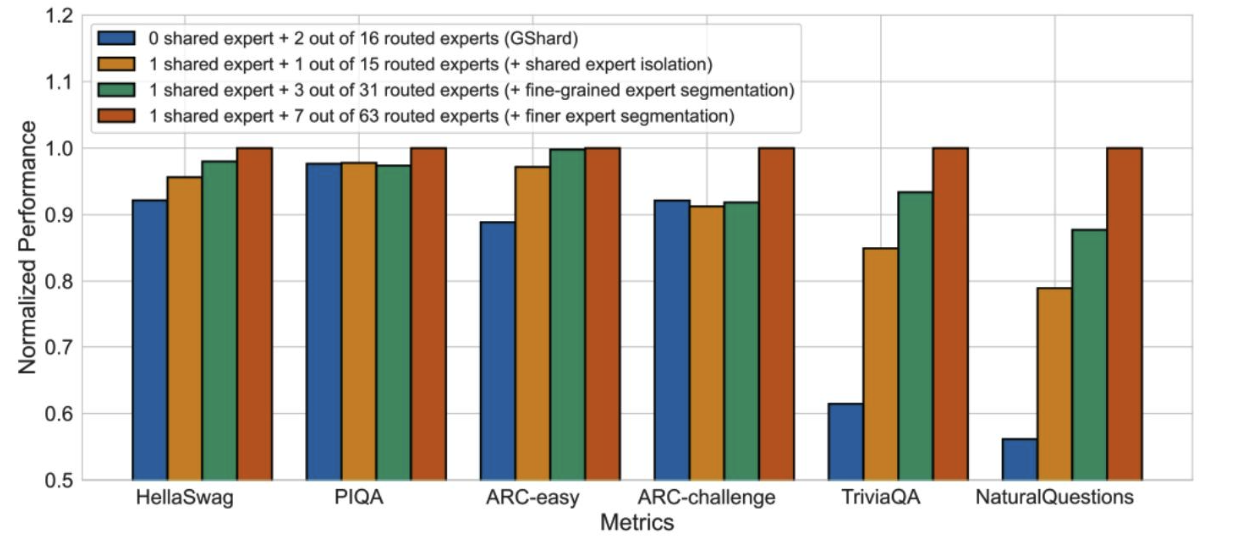
更多的專家、共享專家似乎總體上都有幫助

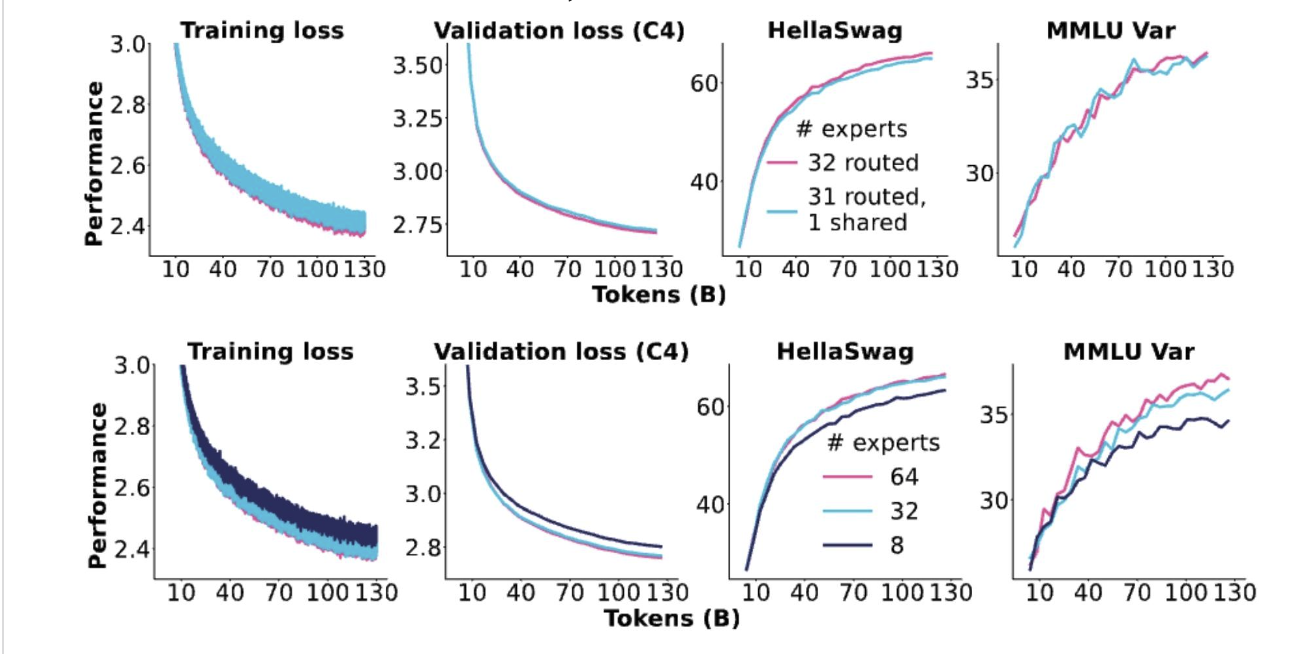
OlMoE的消融實驗

效果都是來自細粒度專家的增益，而沒有來自共享專家的增益。

我們如何訓練混合專家模型（MoEs）？

主要挑戰：為了提高訓練效率，我們需要稀疏性……
但稀疏門控決策是不可微的！
（具體來說，稀疏門控通過路由機制（如 Top-K 路由）選擇部分專家，未被選中的專家對應的門控系數會被設為 0。這種 “非此即彼” 的離散選擇過程（要么選中專家并保留其權重，要么不選中并置零）不存在連續的梯度變化，而深度學習模型的訓練依賴反向傳播算法，需要計算參數關于損失函數的梯度以更新參數。因此，稀疏門控的離散性導致無法直接通過常規的反向傳播對門控相關參數進行優化，給模型訓練帶來了困難）
解決方案？

1. 強化學習優化門控策略
2. 隨機擾動
3. 啟發式“平衡”損失。

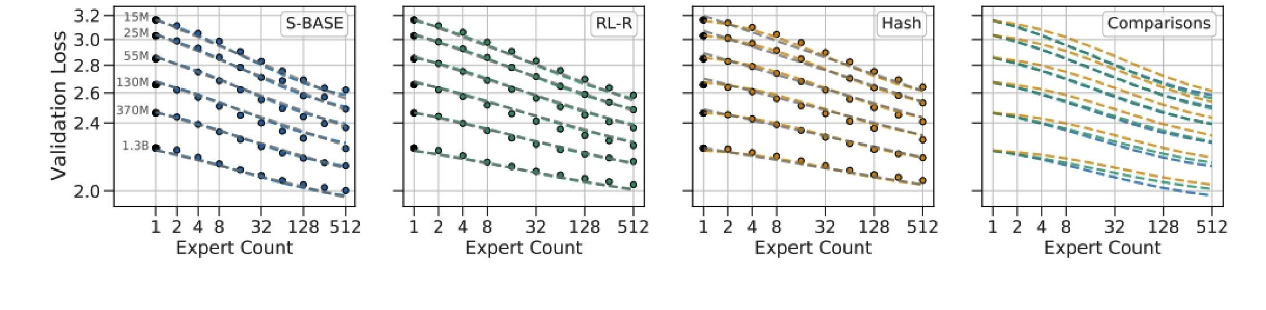
多專家模型的強化學習

通過REINFORCE算法的強化學習確實有效，但并沒有好到能明顯勝出。
強化學習是“正確的解決方案”，但梯度方差和復雜性意味著它并未得到廣泛應用

隨機擾動

出自沙澤爾等人2017年的研究——路由決策是隨機的，伴有高斯擾動。

1. 這自然會產生更具魯棒性的專家。
2. softmax 意味著模型學習如何對 K 個專家進行排序
   

啟發式平衡損失

另一個關鍵問題——系統效率要求我們均衡地使用專家。
輔助損失是向量 f（各專家的 token 分配比例）與 P（各專家的路由概率比例）的縮放點積。通過最小化該損失，可促使模型讓 token 實際分配比例（($f_i$)）與路由概率分配比例（($P_i$)）更接近，從而平衡各專家的負載

深度求索（v1-2）示例

每個專家平衡-與Switch Transformer相同

每個設備平衡-按設備匯總

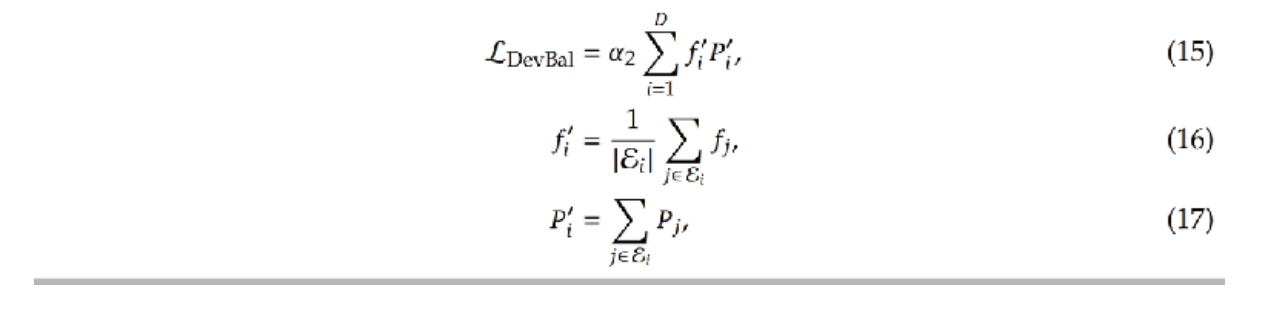
DeepSeek v3變體——專家級偏差

設置每個專家的偏差（使其更有可能獲得詞元）并使用在線學習 gi,t′={si,t,si,t+bi∈Topk({sj,t+bj∣1≤j≤Nr},Kr),0,otherwise.g_{i, t}'= \begin{cases}s_{i, t}, & s_{i, t}+b_{i} \in Topk\left(\left\{s_{j, t}+b_{j} | 1 \leq j \leq N_{r}\right\}, K_{r}\right), \\ 0, & otherwise. \end{cases}gi,t′?={si,t?,0,?si,t?+bi?∈Topk({sj,t?+bj?∣1≤j≤Nr?},Kr?),otherwise.?
他們將此稱為“無輔助損失平衡”

• ($b_i$) 是專家 i 的偏置項，通過在線學習調整：若某專家被分配的 token 過少，($b_i$) 會增大，使其更易被選入 Top-K 專家；若某專家負載過重，($b_i$) 會減小，降低其被選中的概率；

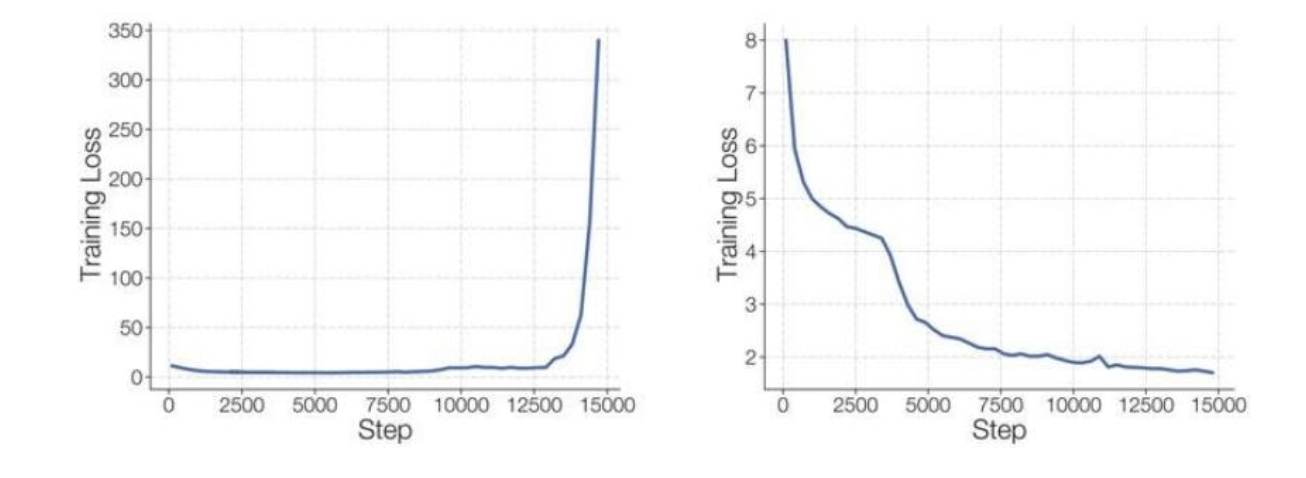
去除負載均衡損失會發生什么？

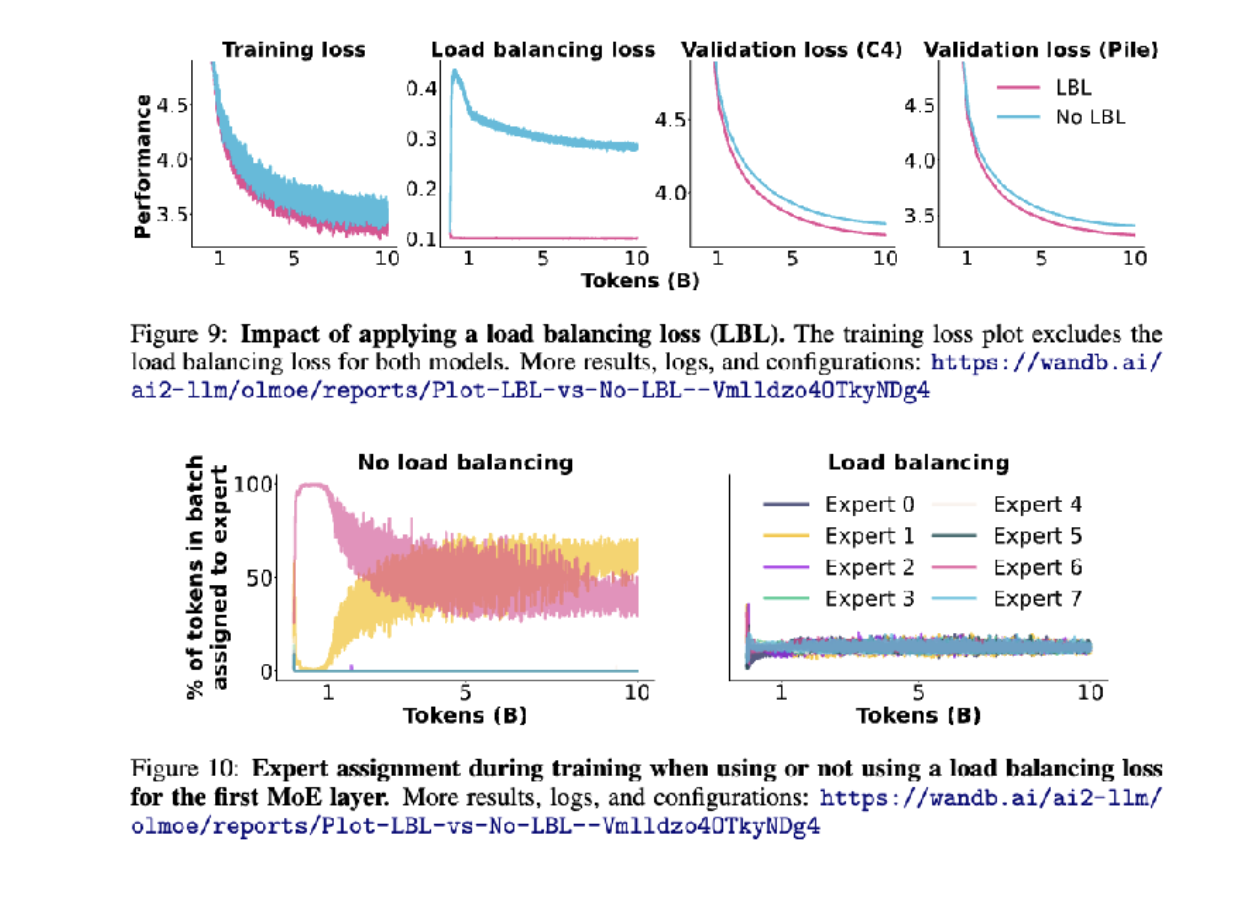
如果不做負載均衡，除了粉色和黃色的模型，其他模型都被浪費了

從系統層面訓練MoEs

混合專家模型（MoEs）的并行性良好——每個前饋神經網絡（FFN）都可以適配一個設備

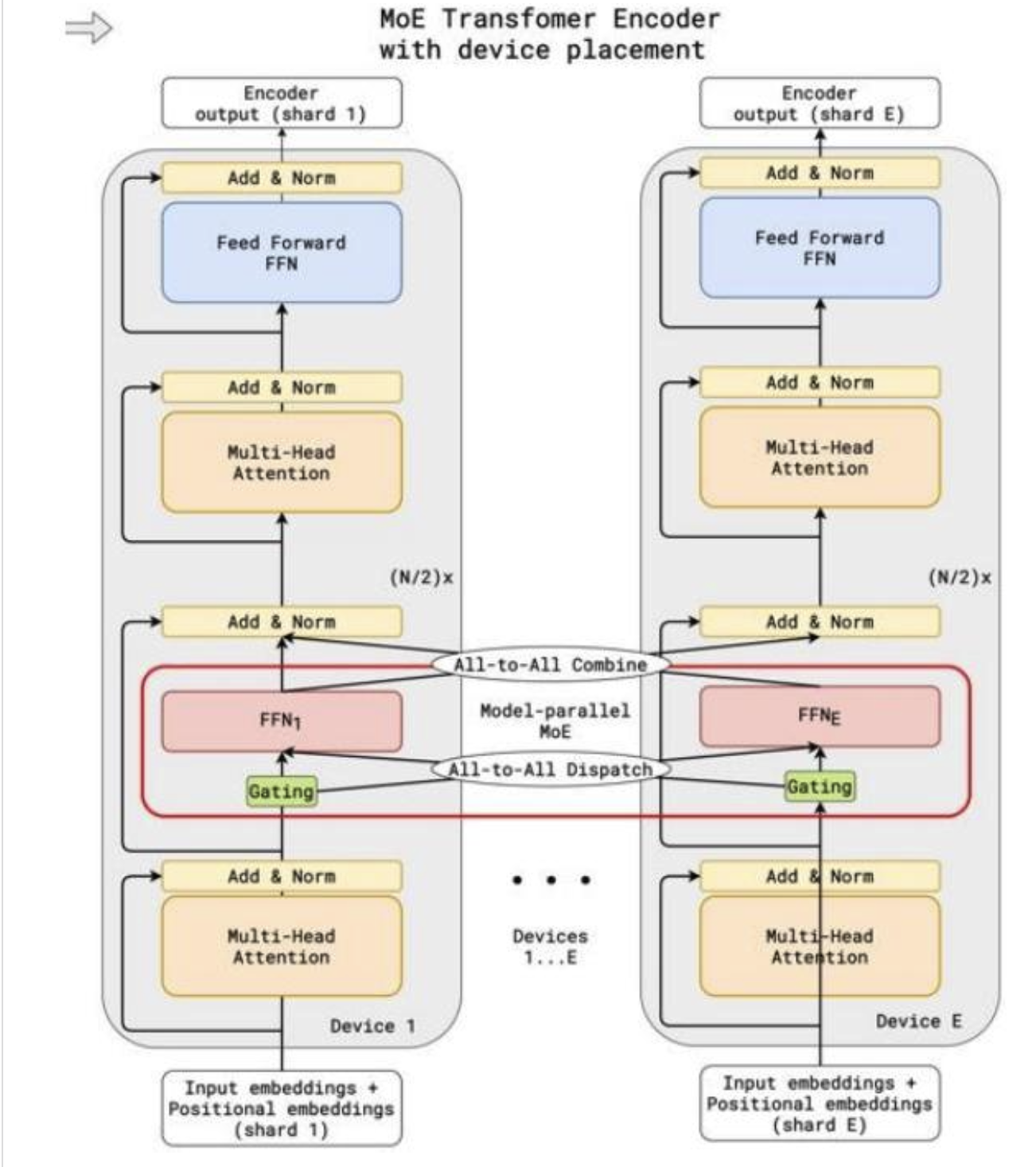
混合專家（MoE）路由允許并行計算，但也存在一些復雜性

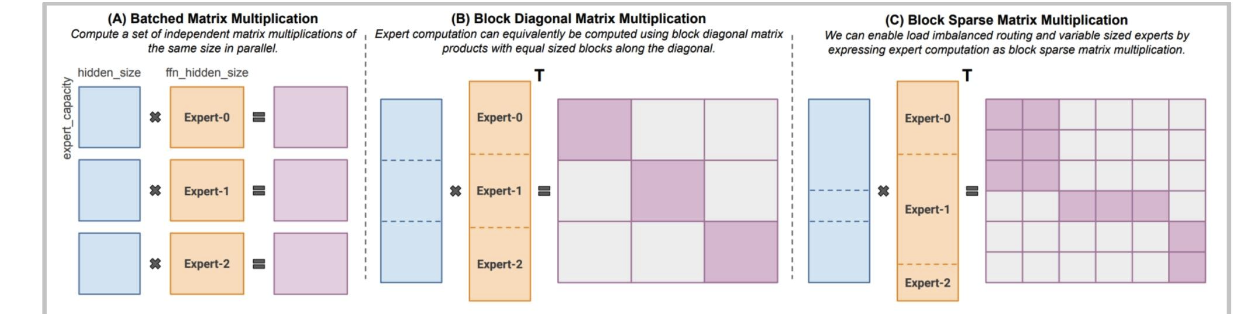
像MegaBlocks這樣的現代庫（在許多開源混合專家模型中使用）采用了更智能的稀疏矩陣乘法運算。

有趣的附帶問題——混合專家（MoE）模型的隨機性

有人猜測GPT-4的隨機性是由于混合專家（MoE）造成的。
為什么混合專家模型（MoE）會有額外的隨機性？

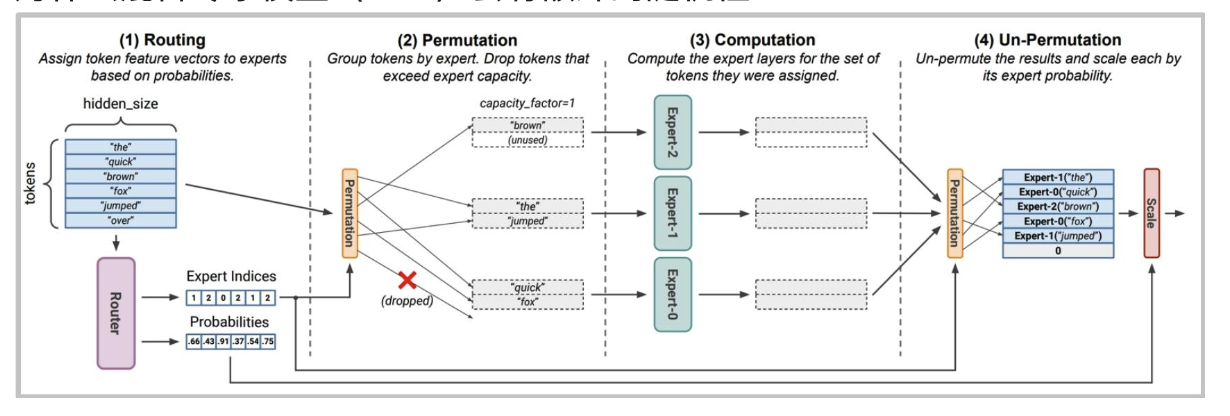
從路由中丟棄令牌是在批次級別進行的——這意味著其他人的查詢可能會丟棄你的令牌！

混合專家模型（MoE）的問題 - 穩定性

解決方案：僅對專家路由器使用Float 32（有時帶有輔助z損失） $L_z(x)=\frac{1}{B}{\sum }_{i=1}^B{\left(log{\sum }_{j=1}^N{e}^{x_j^{(i)}}\right)}^2(5)$

路由器的Z損失穩定性

當我們去掉z損失時會發生什么？

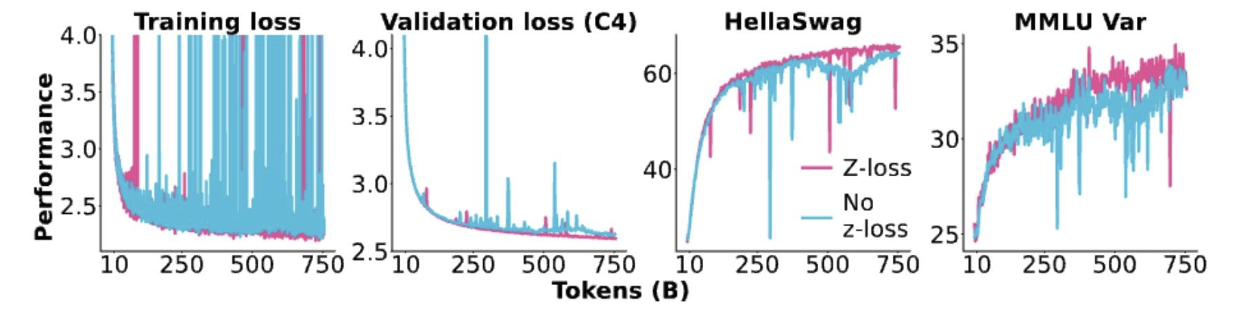
混合專家模型（MoE）的問題——微調

稀疏混合專家模型（Sparse MoEs）在較小的微調數據上可能會過擬合

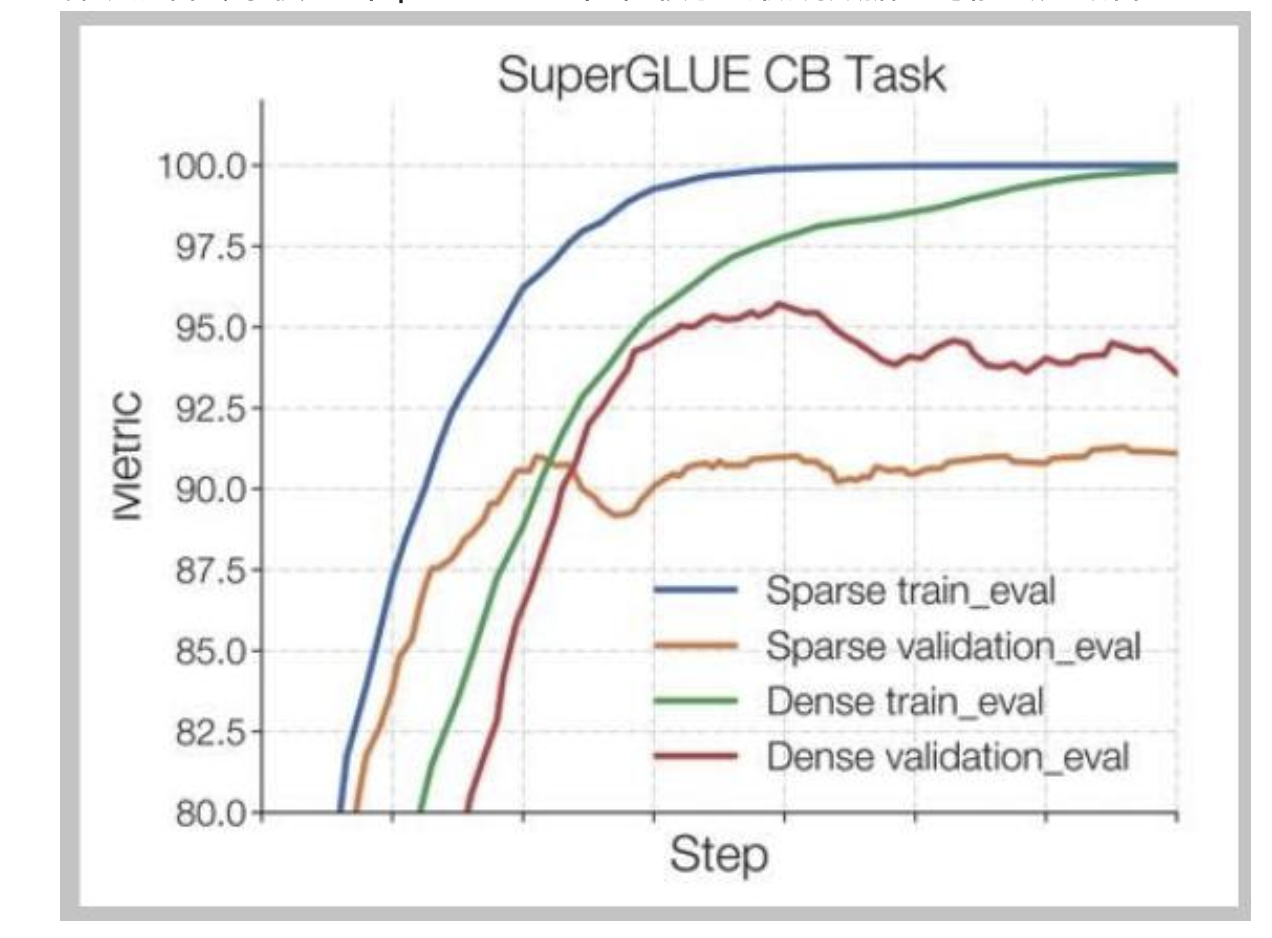
佐夫等人的解決方案——微調非混合專家（MoE）多層感知器（MLP）

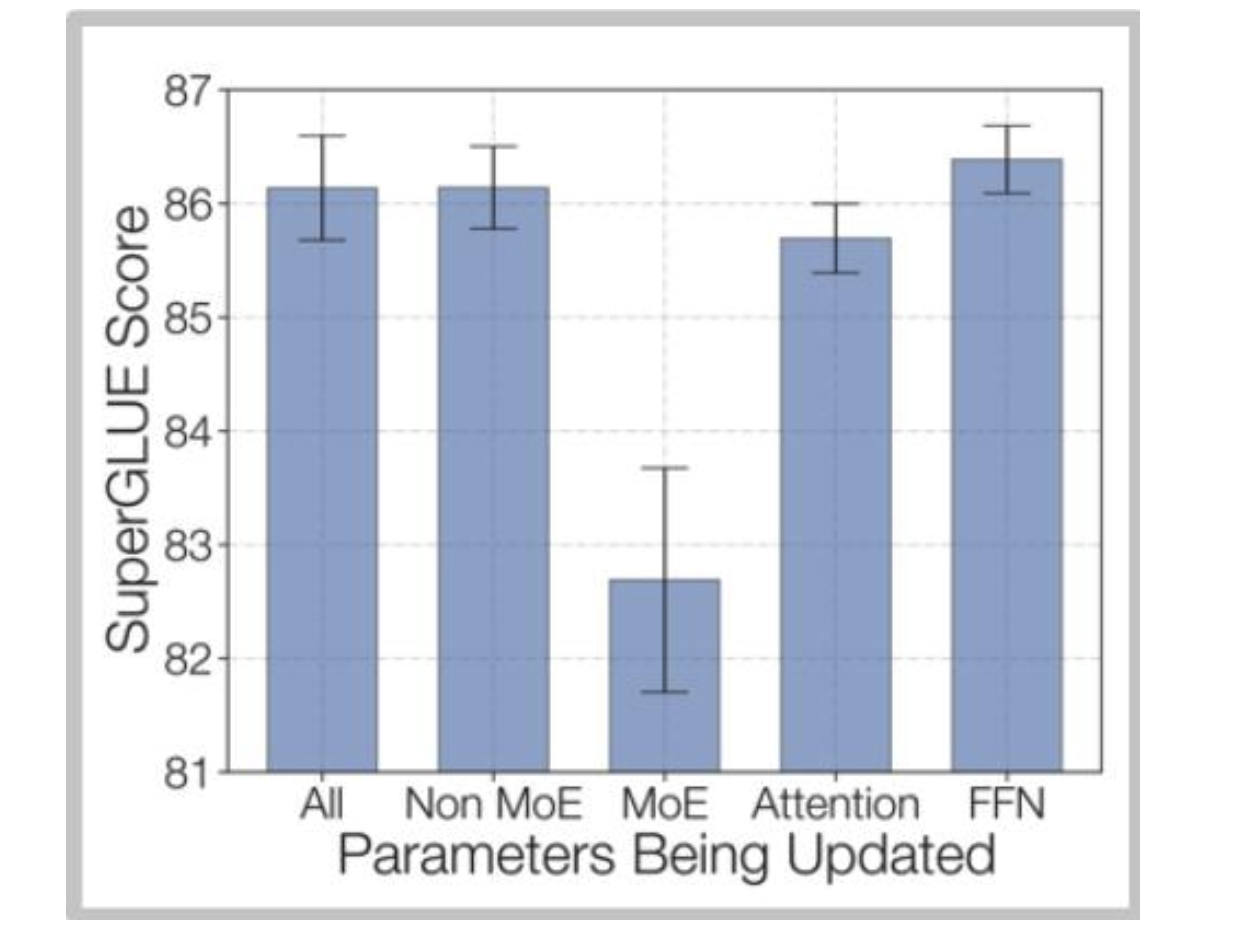
DeepSeek解決方案 - 使用大量數據140萬個監督微調樣本
訓練數據:為了訓練聊天模型，我們使用內部精心整理的數據集進行有監督微調（SFT），該數據集包含140萬個訓練示例。此數據集涵蓋廣泛的類別，包括數學、代碼、寫作、問答、推理、摘要等。我們的有監督微調訓練數據大多為英文和中文，這使得聊天模型用途廣泛，可應用于雙語場景。

其他訓練方法 - 升級循環利用

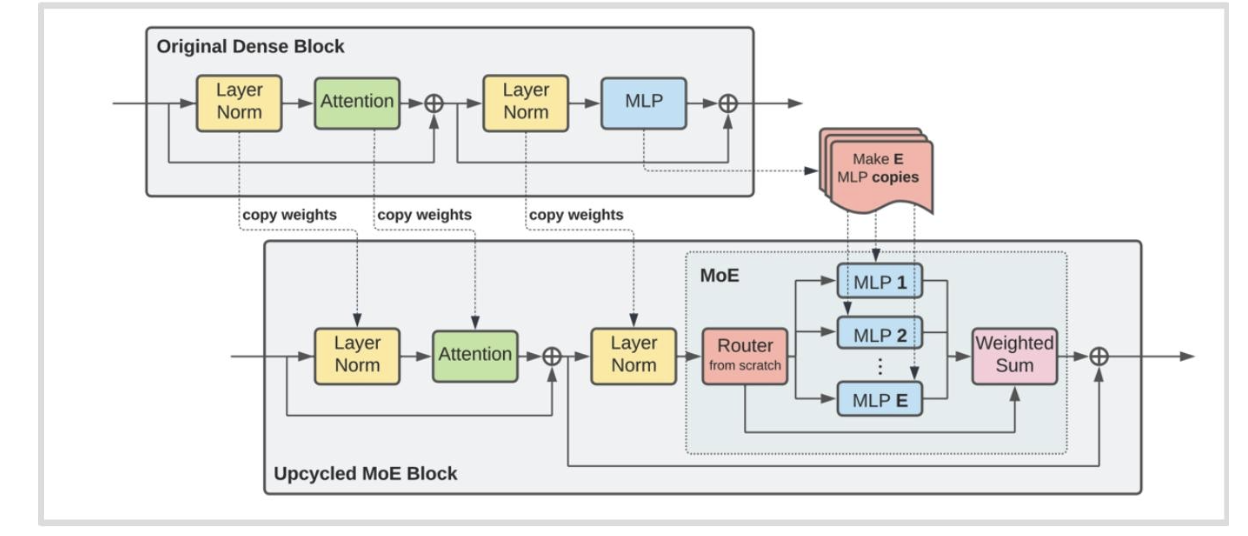
我們可以使用預訓練的大語言模型（LM）來初始化一個混合專家模型（MoE）嗎？

• 原始密集塊中的多層感知機（MLP）模塊被復制了 E 份，形成了混合專家（MoE）模塊中的多個多層感知機。
• 新引入了路由模塊（Router from scratch）來處理輸入并將其分配給不同的多層感知機。
• 最后通過加權求和（Weighted Sum）操作將多個多層感知機的輸出合并。

混合專家模型（MoE）總結

混合專家模型（MoEs）利用了稀疏性——并非所有輸入都需要完整的模型。
離散路由很難，但前 k 啟發式算法似乎可行
現在有大量實證證據表明專家混合模型（MoEs）有效且具有成本效益。

總結

問題1：什么是混合專家模型（MoE），其核心特點是什么？

混合專家模型（MoE）用多個前饋網絡（專家）和一個選擇器層替代傳統大型前饋網絡，核心特點是通過稀疏路由僅激活部分專家，在不顯著增加浮點運算量（FLOPs）的情況下提升參數規模，兼顧效率與性能。

問題2：混合專家模型（MoE）受歡迎的主要原因有哪些？

1.相同FLOPs下，更多參數帶來更好性能；2. 訓練速度更快；3. 與密集模型相比競爭力強；4. 支持專家并行，可將不同專家部署在多個設備上，易于擴展。

問題3：MoE中常見的路由方式有哪些？主流方式的原理是什么？

常見路由方式包括Top-k、哈希、強化學習路由等，主流為Top-k路由。其原理是：輸入通過門控向量計算各專家權重，篩選出權重最高的前k個專家，僅用這些專家處理輸入并加權求和，實現稀疏激活。

問題4：訓練MoE的核心挑戰是什么？有哪些解決方案？

核心挑戰是稀疏門控的離散性導致不可微，難以通過反向傳播優化。解決方案包括：1. 強化學習優化路由（成本高，應用少）；2. 隨機擾動（引入高斯噪聲使路由連續化）；3. 啟發式平衡損失（促使專家負載均衡，如輔助損失調整token分配）。

問題5：MoE存在哪些主要問題，如何應對？

1.穩定性問題：稀疏路由易導致訓練不穩定，可通過對路由器使用float32或添加z損失緩解；2. 微調過擬合：在小數據集上易過擬合，可采用大量微調數據（如DeepSeek用140萬樣本）或微調非MoE的MLP；3. 基礎設施復雜：需支持專家并行，依賴MegaBlocks等庫優化稀疏計算。