數據結構：二叉樹oj練習

在講今天的題目之前，我們還需要講一下二叉樹的以下特點：

對任意一顆二叉樹，如果度為0的節點個數是n0，度為2的節點個數是n2，則有n0=n2+1.

證明：二叉樹總的節點個數是n，那么有n=n0+n1+n2

? ? ? ? ? ?二叉樹的度為n-1=n1*1+n2*2

結合上面兩個式子，就有：n0=n2+1。

完全二叉樹中，度為1的結點數只有0或1兩種可能 。

說明：因為完全二叉樹的結點是連續編號的，最后一層的結點要么是滿的，要么缺少右邊的若干結點，所以度為1的結點最多有1個。

選擇題

題目1

某二叉樹共有 399 個結點，其中有 199 個度為 2 的結點，則該二叉樹中的葉子結點數為（）
A 不存在這樣的二叉樹
B 200
C 198
D 199

解釋：葉子結點的個數等于度為2的節點的個數+1，所以結果是200

題目2

在具有 2n 個結點的完全二叉樹中，葉子結點個數為（）
A n
B n + 1
C n - 1
D n / 2

度為2的節點個數=度為0的節點個數-1，即n2=n0-1

由于是完全二叉樹，度為1的節點個數只有0或1兩種可能。

如果度為1的節點個數為1，那么1+n0+n0-1=2n，就能得到n0=n，即A可選

如果度為1的節點個數為0，那么n0+n0-1=2n，就會得到n0=（2n+1）/ 2，這是一個小數，所以不合理。

綜上，這道題的答案選A。

題目 3

一棵完全二叉樹的結點數為 531 個，那么這棵樹的高度為（）
A 11
B 10
C 8
D 12

我們知道，二叉樹第k層節點個數為2^(k-1),前k層節點個數為2^(k)-1

假設完全二叉樹的高度為h，那么完全二叉樹節點個數的范圍是： 2^(h-1)再到2^(h)-1.

這個范圍是咋來的呢？首先第一個范圍，既然一共有h層，那么根據公式，前h-1層就一共有2^(h-1)-1個節點，而第h層最少有1各節點，所以前h層應該至少是有2^(h-1)個節點。當這個樹為滿二叉樹時，節點個數達到最大，前h層節點個數一共是：2^(h)-1。

結合這個范圍，我們就可以求得答案是10，即選B

題目 4

一個具有 767 個結點的完全二叉樹，其葉子結點個數為（）
A 383
B 384
C 385
D 386

假設節點個數是n，那么結合結論，n=2*n0-1+n1，我們知道，完全二叉樹的節點個數要么是0，要么是1，帶入公式中我們可以得到，n0=384，此時n1=0

題目 5

二叉樹的先序遍歷和中序遍歷如下：前序遍歷：EFHIGJK；中序遍歷：HFIEJKG。則二叉樹后續遍歷序列：（）

如果我們知道前序遍歷+中序遍歷? 或者? 中序遍歷+后序遍歷，就可以推導出二叉樹的結構。

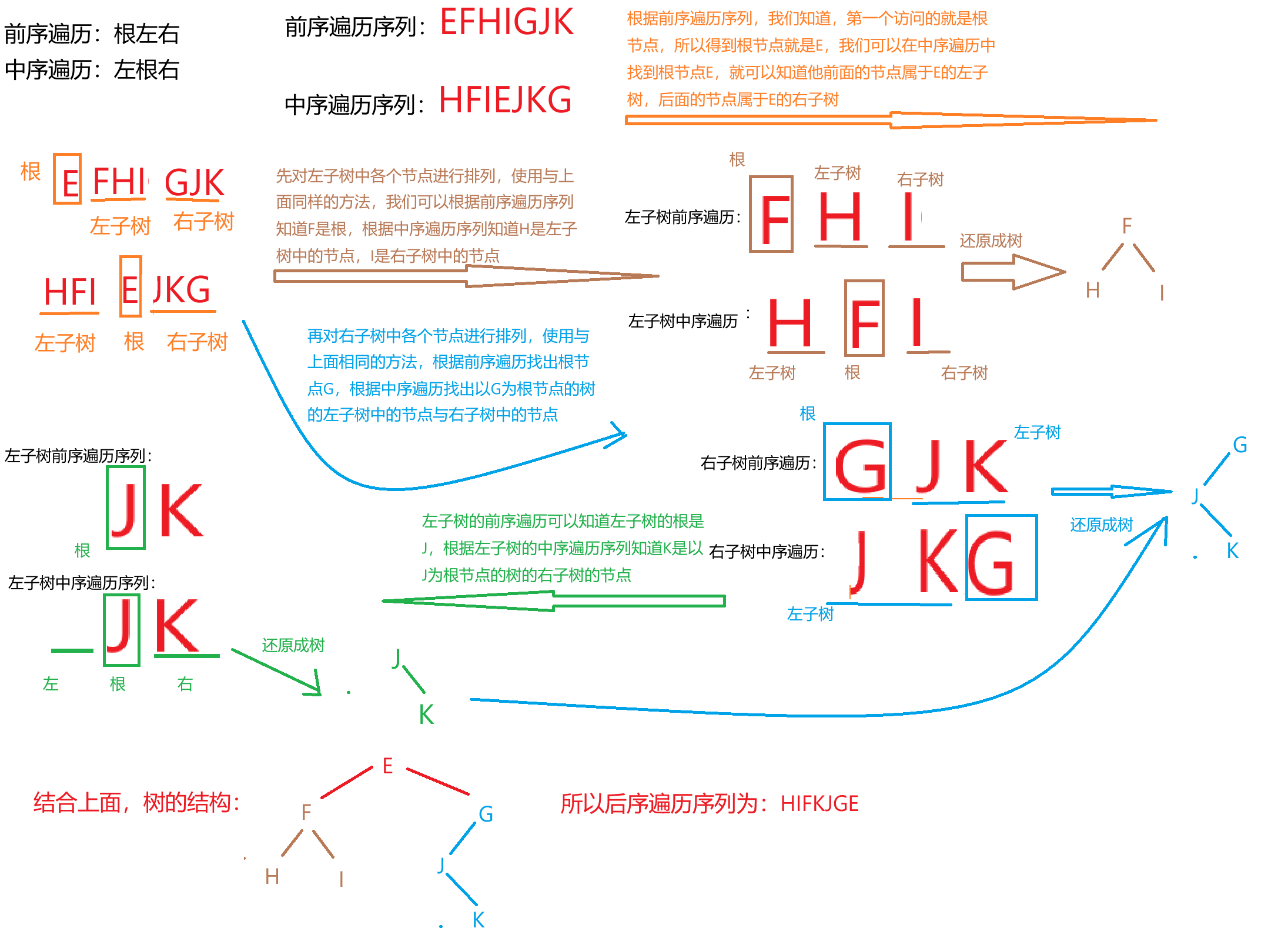
題目 6

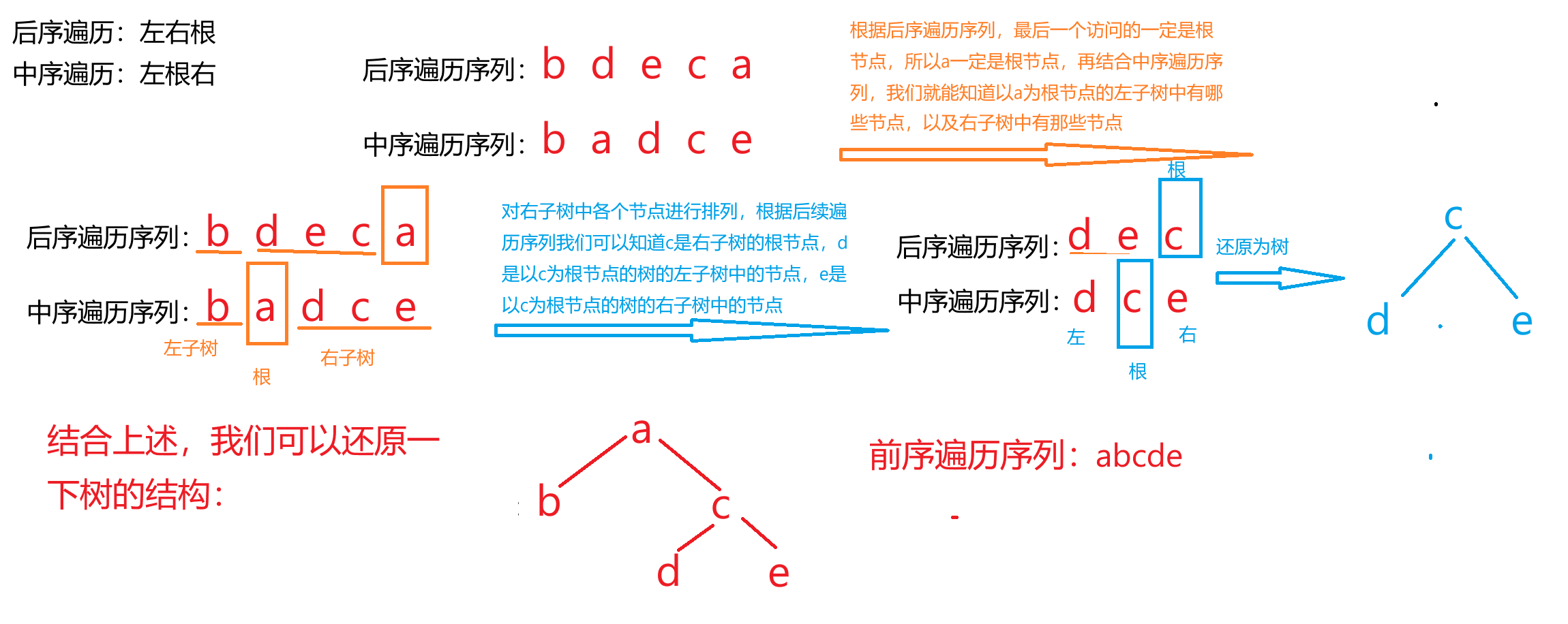
設一棵二叉樹的中序遍歷序列：badce，后序遍歷序列：bdeca，則二叉樹前序遍歷序列為____。 A.?adbce

B.?decab

C.?debac

D.?abcde

編程題

144. 二叉樹的前序遍歷 - 力扣（LeetCode）

這道題就是簡單的前序遍歷，我們之前在二叉樹的實現方法中已經寫過了，只需要將代碼稍加修改就可以咯：

 void preorder(struct TreeNode* root,int*res, int* returnSize){if(root==NULL){return ;}//先存根節點res[(*returnSize)++]=root->val;preorder(root->left,res,returnSize);preorder(root->right,res,returnSize);}
int* preorderTraversal(struct TreeNode* root, int* returnSize) 
{*returnSize=0;//樹中節點的數目在100內int*res=(int*)malloc(sizeof(int)*100);//前序遍歷preorder(root,res,returnSize);return res;
}

145. 二叉樹的后序遍歷 - 力扣（LeetCode）

void postorder(struct TreeNode* root, int* res, int* returnSize)
{if (root == NULL){return;}postorder(root->left, res, returnSize);postorder(root->right, res, returnSize);res[(*returnSize)++] = root->val;
}int* postorderTraversal(struct TreeNode* root, int* returnSize) {*returnSize = 0;//樹中節點的數目在100內int* res = (int*)malloc(sizeof(int) * 100);//后序遍歷postorder(root, res, returnSize);return res;
}

94. 二叉樹的中序遍歷 - 力扣（LeetCode）

 void inorder(struct TreeNode* root, int* res, int* returnSize)
{if (root == NULL){return;}inorder(root->left, res, returnSize);res[(*returnSize)++] = root->val;inorder(root->right, res, returnSize);}int* inorderTraversal(struct TreeNode* root, int* returnSize) {*returnSize = 0;//樹中節點的數目在100內int* res = (int*)malloc(sizeof(int) * 100);//中序遍歷inorder(root, res, returnSize);return res;}

965. 單值二叉樹 - 力扣（LeetCode）

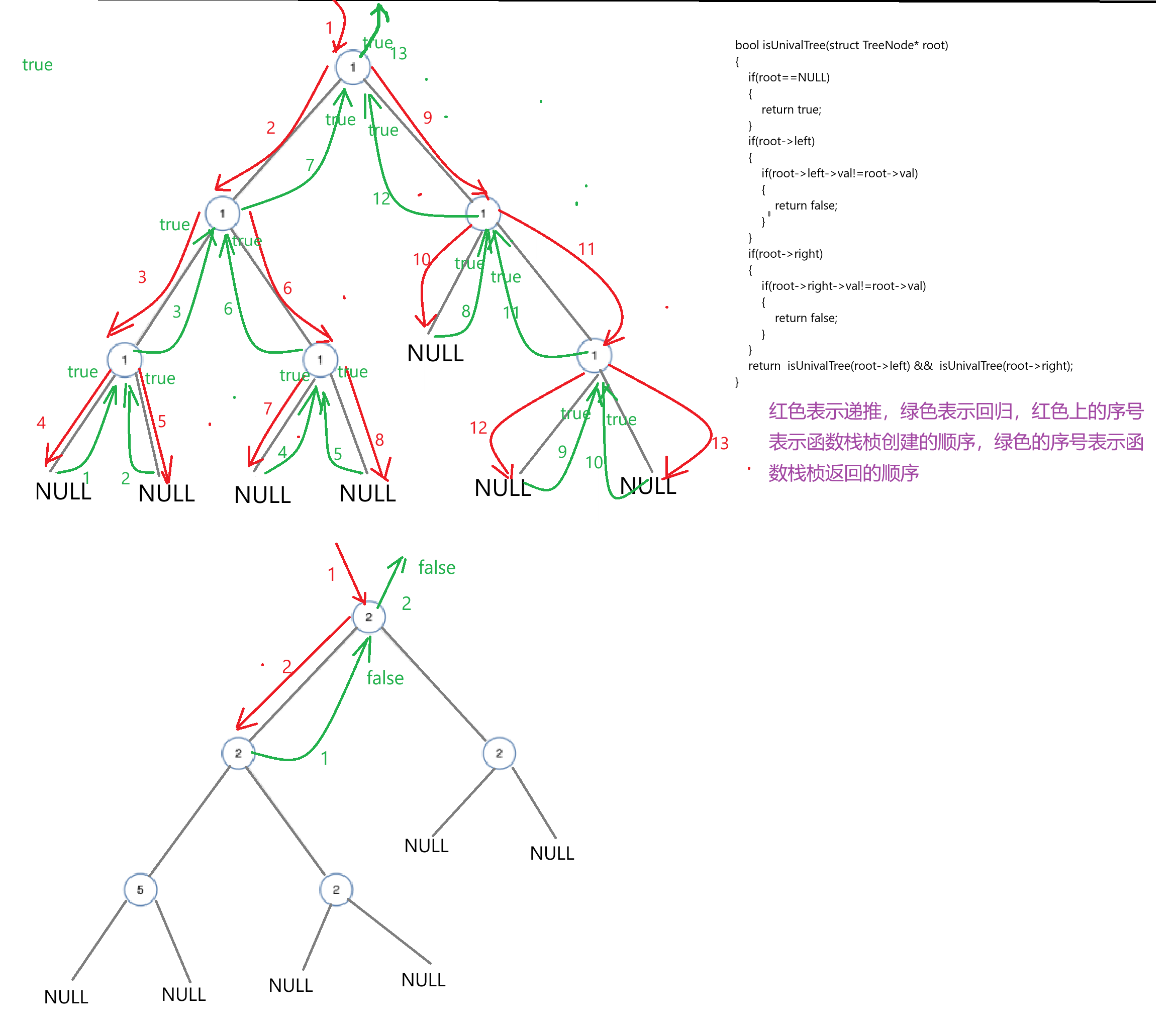
這一道題的簡單思路也是遞歸，如果一棵樹是單值樹，那么他的子樹也是單值樹，那我們就可以把大問題拆分成若干個子問題了：

bool isUnivalTree(struct TreeNode* root) 
{if(root==NULL){return true;}if(root->left){if(root->left->val!=root->val){return false;}}if(root->right){if(root->right->val!=root->val){return false;}}return  isUnivalTree(root->left) &&  isUnivalTree(root->right);
}

我們可以模擬一下遞歸過程：

100. 相同的樹 - 力扣（LeetCode）

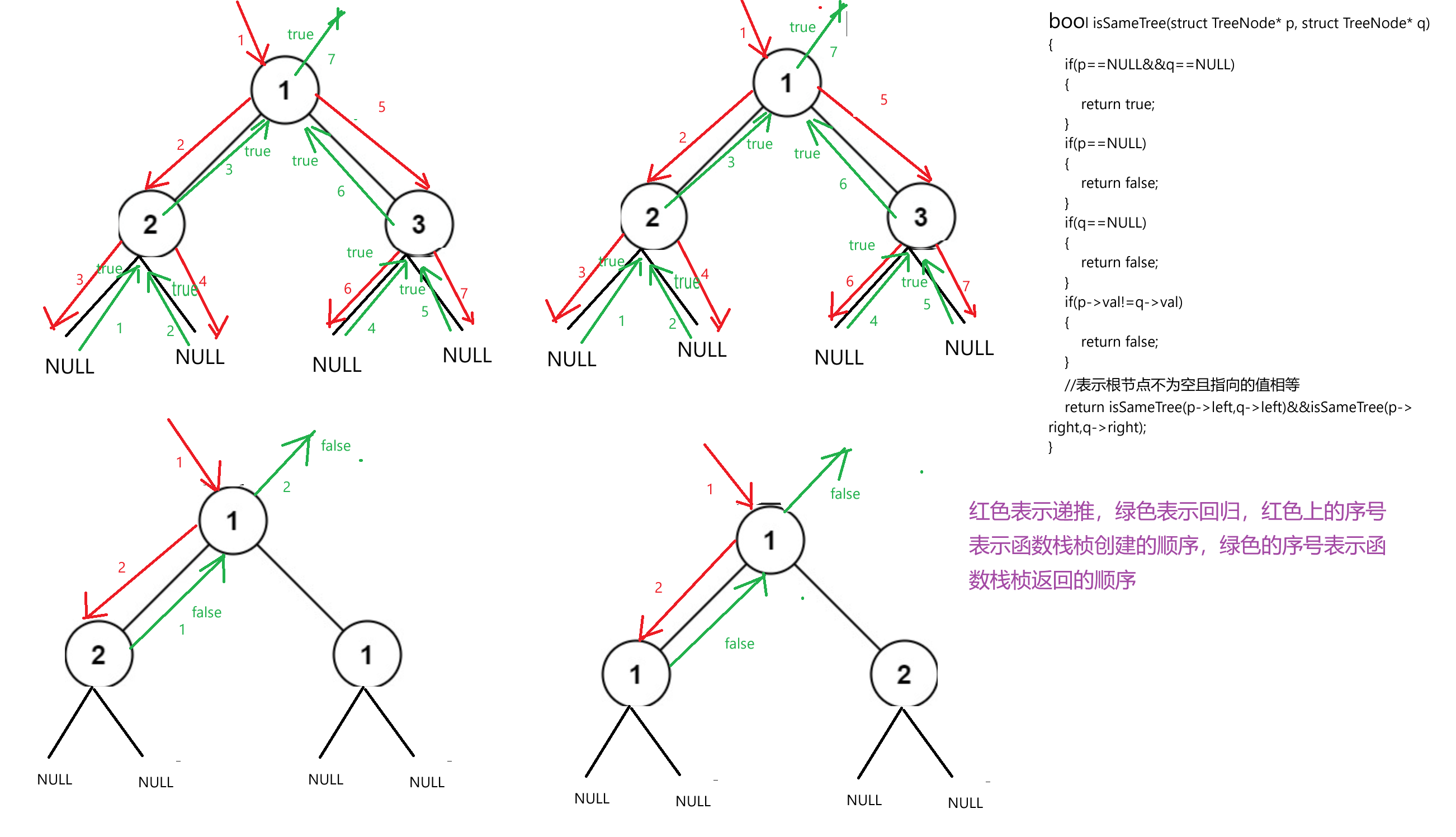
這道題的思路也是利用遞歸，如果兩顆樹的根節點相同，那就只需要再比較兩顆樹的左右子樹是否相同即可：

bool isSameTree(struct TreeNode* p, struct TreeNode* q) 
{if(p==NULL&&q==NULL){return true;}if(p==NULL){return false;}if(q==NULL){return false;}if(p->val!=q->val){return false;}//表示根節點不為空且指向的值相等return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}

我們可以模擬一下遞歸過程：

101. 對稱二叉樹 - 力扣（LeetCode）

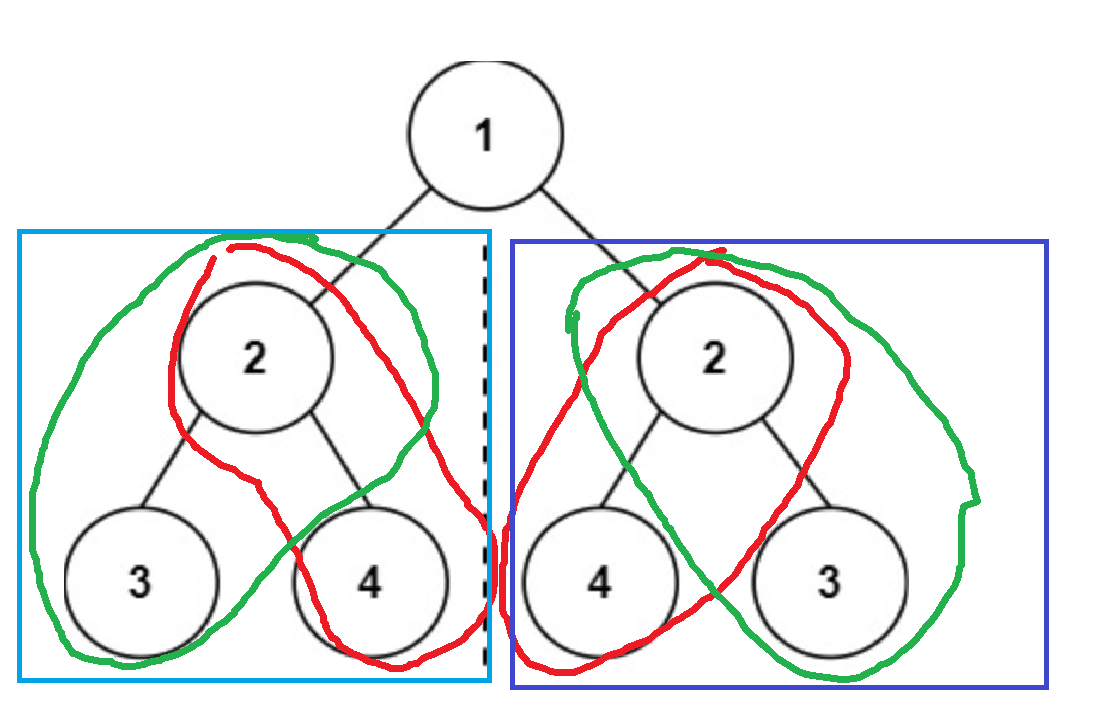
如圖，判斷一個樹是否是對稱二叉樹，就是要比較根節點的左右子樹，我們可以把根節點的左右子樹看成兩棵獨立的二叉樹，問題就轉換為比較這兩棵樹是否對稱。

兩棵樹是否互為對稱樹，就是比較樹A上某個節點的左孩子節點的值與樹B上對應節點的右孩子節點的值以及樹A上某個節點的右孩子節點的值與樹B上對應節點的左孩子節點的值是否相等，如果相等的話，就繼續遞歸比較孩子節點的值。

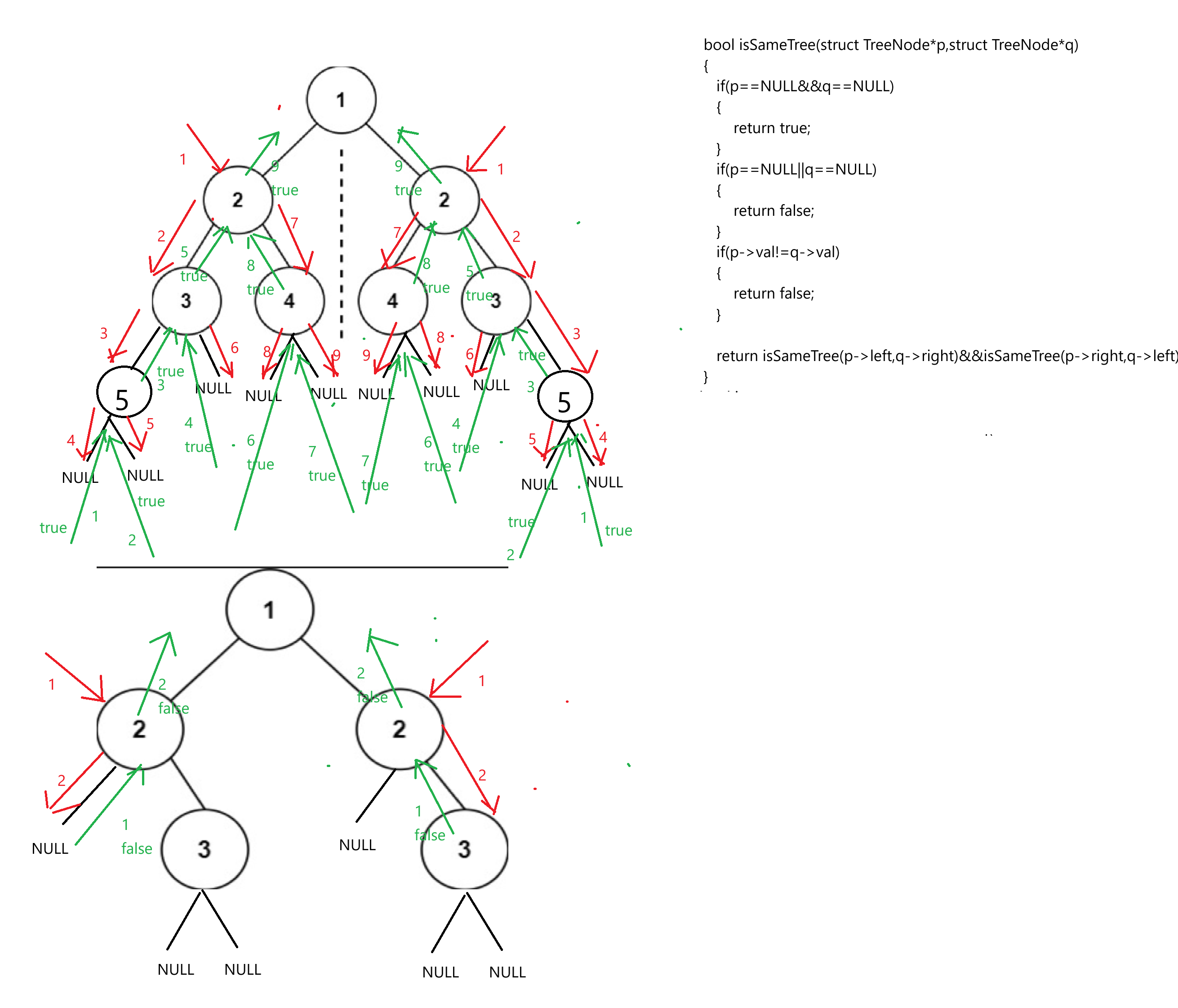
 bool isSameTree(struct TreeNode*p,struct TreeNode*q){if(p==NULL&&q==NULL){return true;}if(p==NULL||q==NULL){return false;}if(p->val!=q->val){return false;}//兩棵樹根節點相同，再比較樹A的左孩子與樹B的右孩子是否相同，以及樹A的右孩子與樹B的左孩子是否相同return isSameTree(p->left,q->right)&&isSameTree(p->right,q->left);}
bool isSymmetric(struct TreeNode* root)
{return  isSameTree(root->left,root->right);
}

模擬遞歸過程：

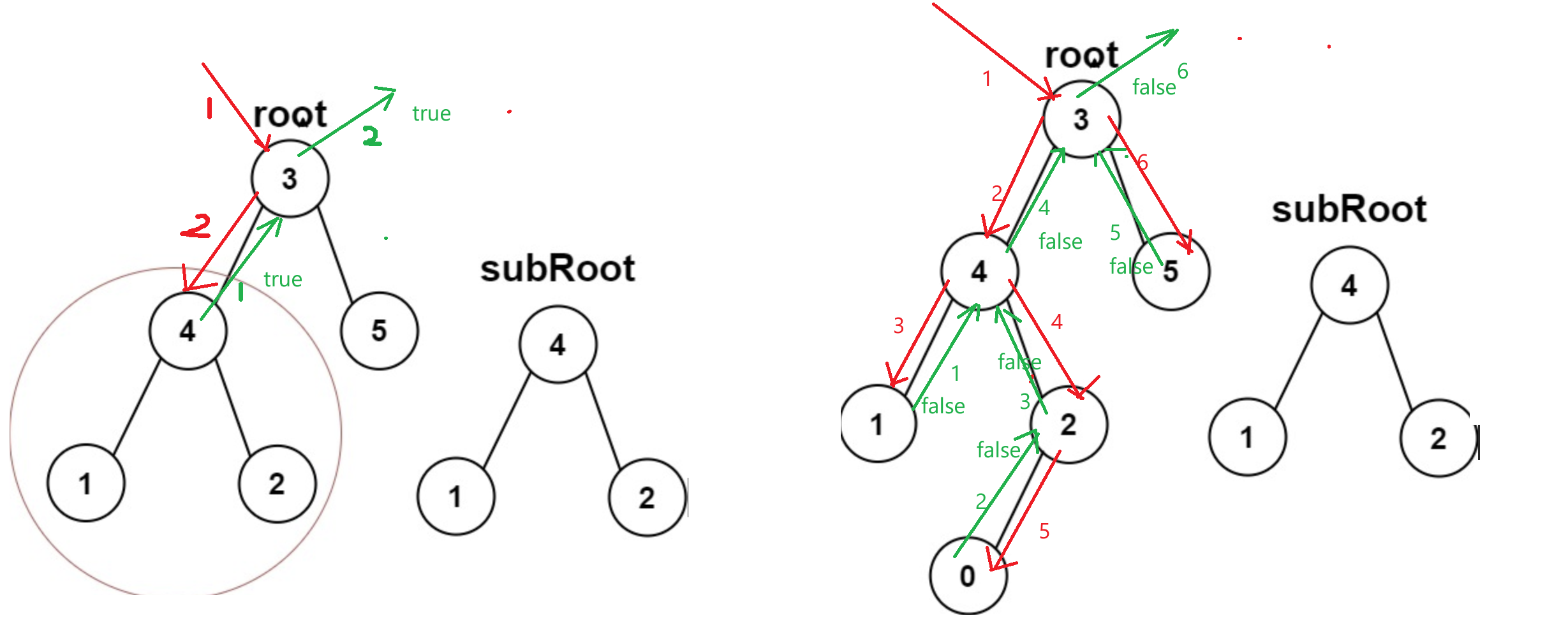
572. 另一棵樹的子樹 - 力扣（LeetCode）

這一體的思路比較好想，我們可以先比較subroot是否與整棵樹相同，如果相同，那就可以直接返回了，如果不相同，說明subroot可能是樹的子樹，就需要遍歷整棵樹的節點，看是否存在以某一個節點為根的樹與subroot相同：

bool isSameTree(struct TreeNode* p, struct TreeNode* q) 
{if(p==NULL&&q==NULL){return true;}if(p==NULL){return false;}if(q==NULL){return false;}if(p->val!=q->val){return false;}//表示根節點不為空且指向的值相等return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) 
{if(subRoot==NULL){return true;}if(root==NULL){return false;}if(isSameTree(root,subRoot)){return true;}return isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);
}

二叉樹遍歷_牛客題霸_牛客網

我們之前說過，如果知道前序遍歷+中序遍歷? 或者? 中序遍歷+后序遍歷，就可以推導出二叉樹的結構。但是現在題目中只給了我們前序遍歷的結果，我們還能根據這個去構建二叉樹的結構嗎？

在這一題中是可以的，因為題中給我們的字符串是帶有'#'的，這表示空指針，前序遍歷的順序是按照根節點->左子樹->右子樹，當我們遇到‘#’的時候，就無法繼續往下遍歷，而是要回到原來子樹的根，這沒說這可能有點抽象，我們利用題目中給的測試樣例來手動還原二叉樹的結構：

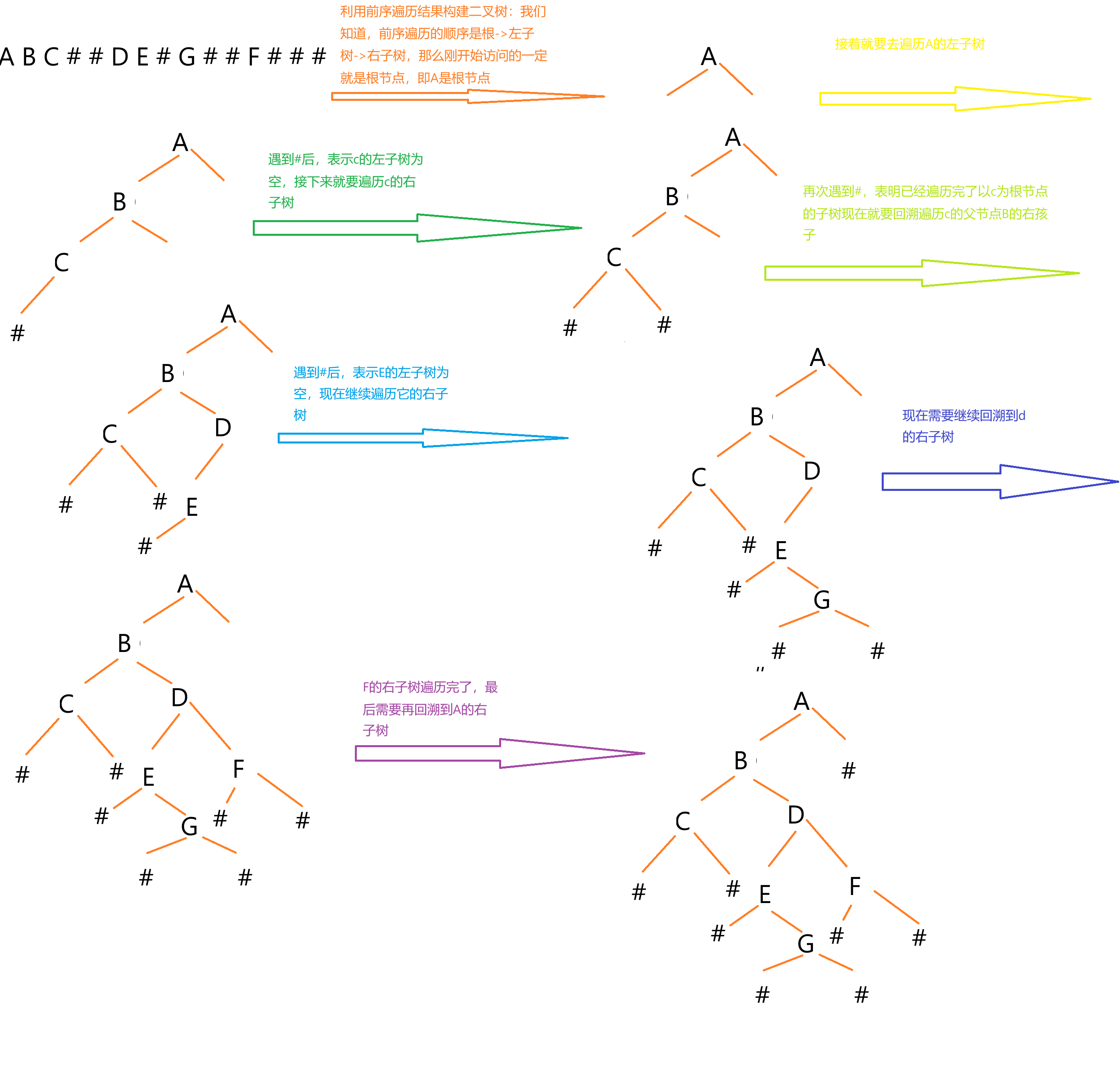
利用遍歷結果構建二叉樹聽起來好像挺難的，但其實就是對二叉樹進行遍歷，我們在寫前序遍歷的代碼的時候，將訪問二叉樹的節點的操作寫成了打印二叉樹的節點值，在這里，無非就是讓我們在前序遍歷過程中將訪問二叉樹的節點的操作寫成了創建節點呀，具體思路還是沒有變呀，那我們就繼續寫一下代碼吧：

//二叉樹的構建與遍歷
#include<stdio.h>
#include<stdlib.h>
//二叉樹的節點的定義
typedef struct btnode {char data;struct btnode* left;struct btnode* right;
} btnode;btnode* buynode(char x) {btnode* newnode = (btnode*)malloc(sizeof(btnode));newnode->data = x;newnode->left = newnode->right = NULL;return newnode;
}//最后返回根節點
//pi表示指向的字符在字符數組中的下標，由于形參的改變需要影響實參，所以我們這里采用傳址調用
btnode* precreattree(char* ch, int* pi) {if (ch[*pi] == '#') {(*pi)++;return NULL;}//先創建根節點btnode* root = buynode(ch[(*pi)++]);//再創建左子樹root->left = precreattree(ch, pi);//創建右子樹root->right = precreattree(ch, pi);//返回根節點return root;
}
//中序遍歷樹的節點
void inorder(btnode* root) {if (root == NULL) {return;}//先遍歷左子樹inorder(root->left);//再訪問根節點printf("%c ", root->data);//再遍歷右子樹inorder(root->right);
}
int main() {char ch[100];//輸入字符串scanf("%s", ch);//輸入的字符串是二叉樹前序遍歷的結果，我們需要根據這個結果去創建二叉樹int i = 0;btnode* root = precreattree(ch, &i);//中序遍歷inorder(root);return 0;
}

今天的內容還是比較豐富的，這些算法題也是比較經典的，能看到這里的兄弟們我真的覺得你們很棒，大家在自己的電腦上也要好好把代碼敲一下，把圖畫一下，把思路整理一下哦！！