EDA（Exploratory Data Analysis，探索性數據分析）是一種在正式建模前，通過統計量和可視化方法來理解數據特征、發現模式與異常、并提出假設的過程。

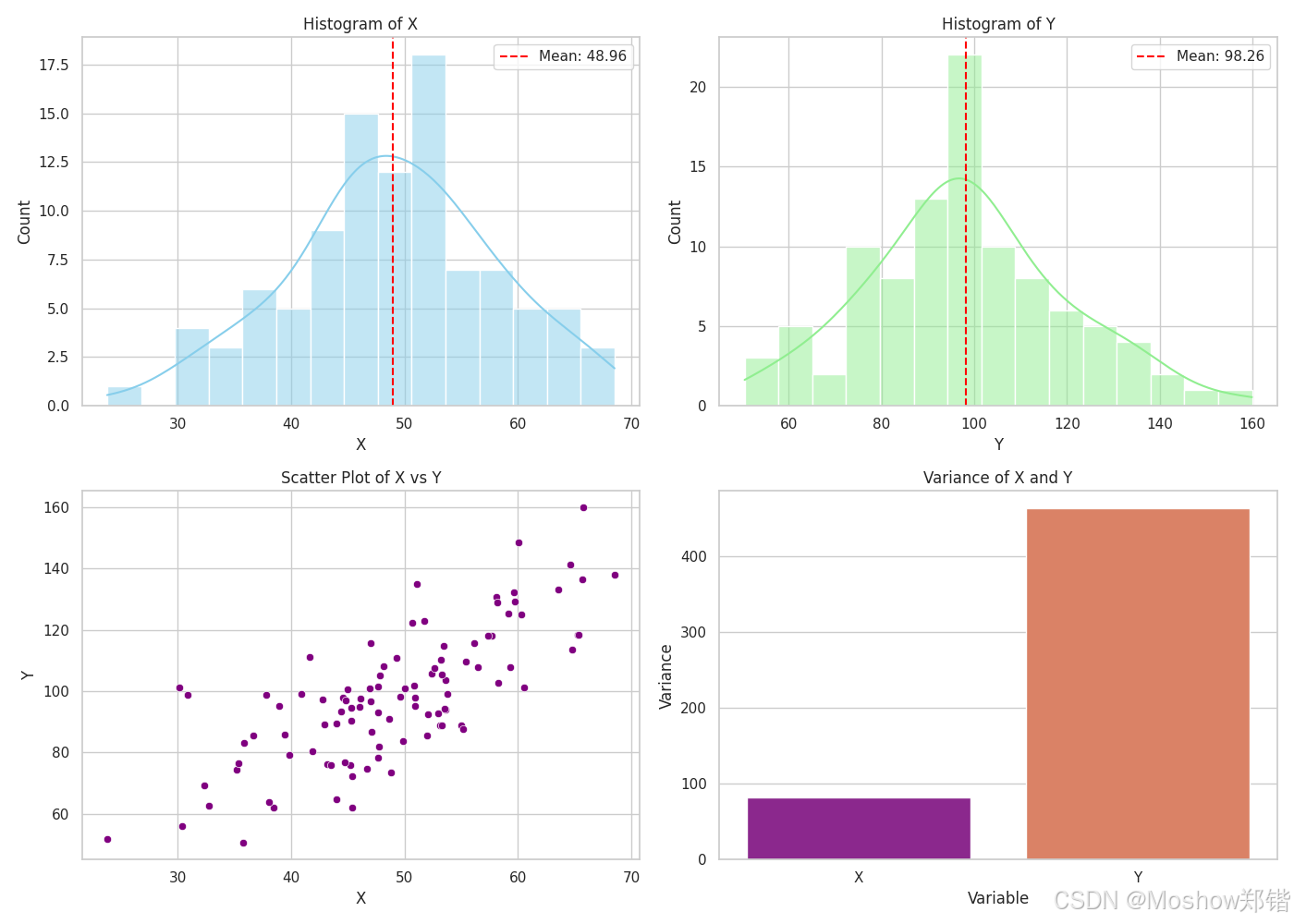
這張圖里你會看到：

• 直方圖：展示單變量的分布，并用紅色虛線標出平均值，幫助理解集中趨勢

• 散點圖：揭示兩個變量之間的關系和可能的相關性

• 方差柱狀圖：直觀比較不同變量的波動大小

• 均值標注：讓你快速定位數據的中心位置

******? 整理 by?Moshow鄭鍇@https://zhengkai.blog.csdn.net/

這里再用表格梳理一下“平均值+方差、散點圖+直方圖”在 EDA 中的作用👇

方法/指標	類型	主要作用	優點	常見注意點
平均值 (Mean)	描述性統計	衡量數據的集中趨勢	直觀易懂，計算簡單	容易受極端值影響
方差 (Variance)	描述性統計	衡量數據離散程度	能反映波動大小	受量綱影響，需要配合標準差使用
散點圖 (Scatter Plot)	可視化	觀察兩變量之間的關系、趨勢或聚類	能發現相關性與離群點	當數據量太大時可能變得難以辨別
直方圖 (Histogram)	可視化	顯示單變量的分布形態	清晰展示分布特征和偏態	組距選擇影響效果

💡 小貼士：

• 平均值+方差適合做數值型特征的整體概覽

• 散點圖更適合找變量之間的關系

• 直方圖能幫助識別分布是否偏態、是否存在多峰