矢量的客觀性和主觀性
宇宙中飄過來一個自由矢量,全世界的人都可以看到,大家都在想,怎么描述它呢,總不能指著它說“那個矢量”吧。數學家很聰明,于是建立了一個坐標系,這個矢量投影到坐標系下,就得到了幾個數,就用這幾個數就可以描述這個矢量了。
這招確實不錯,但是問題來了,沒有這組數字,大家腦子中的矢量是客觀且抽象的,有了這組數字矢量就變成了建坐標系的這個人的了,問題出現了,每個人都可以建立自己的坐標系去描述這個矢量,矢量存在的客觀性和坐標系描述的主觀性之間產生了矛盾。
保留客觀性,沒有具體的數字,不好計算,選擇了坐標,倒是容易計算了,但是每個人眼中的矢量就又不一樣了。
數學家給出的辦法是,先讓一個朋友主觀的選擇一個坐標系,用一組坐標數字描述這個矢量,然后在給出一個所有坐標系的之間的變換,這樣,每個人都能拿著一組任意的主觀的坐標數據通過一定的變換關系變換到自己的主觀坐標系下,也就是說,一個主觀+一組變換方法,可以換得全世界所有的主觀視角,一旦我們掌握了所有的主觀視角,主觀到了極限,我們便再次擁有了客觀。
基變換
在線性代數的學習中,n維空間中的n維向量的元素常常是由相對獨立的因素組成的,這些相對獨立的因素或者完全獨立(垂直或者正交),或者相對獨立(線性無關,我有你沒有的部分)。對于n維空間的幾何圖形的想象,坐標軸的現實意義上的垂直不是必須的,如果幾何意義上的垂直或者正交代之以代數意義上的線性無關概念,取消了幾何作圖對垂直的要求,我們的平面就可以通過斜坐標系畫出來了,就可以形象理解了由n個線性無關向量張成的n維空間的理論,進而想象高維空間的圖像也就不是一件特別困難的事情了。
空間本身并沒有內蘊的網格,每種基下的宇宙空間生物都可以按照基的方向繪制自己的網格,是有助于幫助理解它所在的空間的工具,網格是主觀的,不同的網格空間通過變換達到對方的網格,實現坐標系的切換。因為所有的向量乘以0都是零向量,不同的坐標系下的宇宙生物對0向量的位置可以達成共識。

空間中的兩個點決定了一個自由向量,把所有自由向量的初始點全部拉到坐標原點,這樣平面中的任意一個點就可以和一個向量對應上了(用群的觀點看,是一種自由向量和笛卡爾坐標系中點的之間的同構)。
自由向量的坐標是可以看成是2個標量,這兩個標量的值和坐標系基的選取有直接關系,因為基向量正是這兩個標量縮放的對象。
可以把基向量看成是隱藏于空間坐標系網格中的隱含假設,基變換是說,任何兩個線性無關的向量都可以作為新的坐標系的基定義新的網格,并通過將新基定義為完成加冕。
無論新基是否正交,我們都可以在該坐標系下將基向量自身視為。坐標系切換的本質就是重新定義“單位向量”,與基的正交性無關。非正交性僅導致內積計算不同,但線性變換的代數描述完全自洽。
只要不涉及角度,距離等的度量,可以將任意兩個線性無關的向量作為(1,0)和(0,1)而產生新的坐標宇宙,因為這兩個向量就是定義坐標(1,0)和(0,1)含義的向量。
一個很自然的問題是,我們如何在不同基下進行坐標變換?
坐標變換
問題,在基下的坐標向量(-1,2),如何變換成我們的坐標系下的坐標?
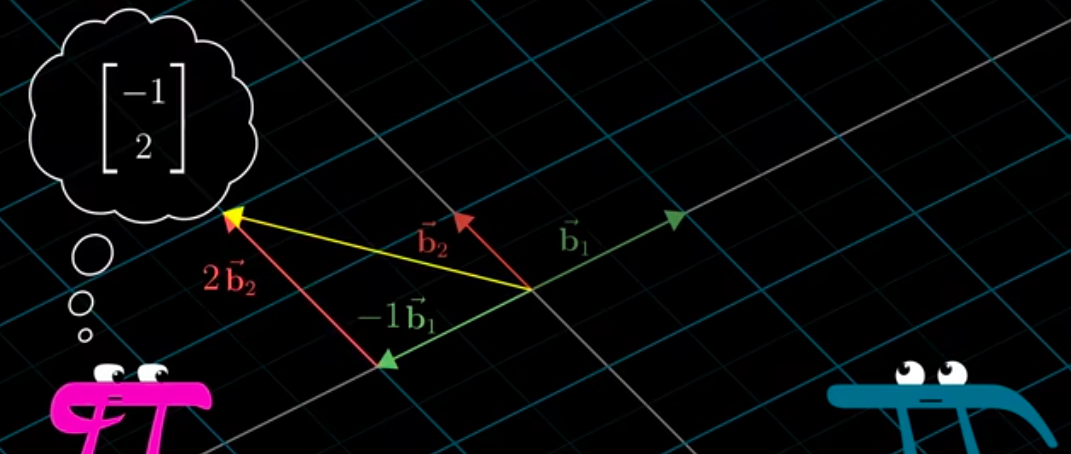
轉換到我們的坐標系下:
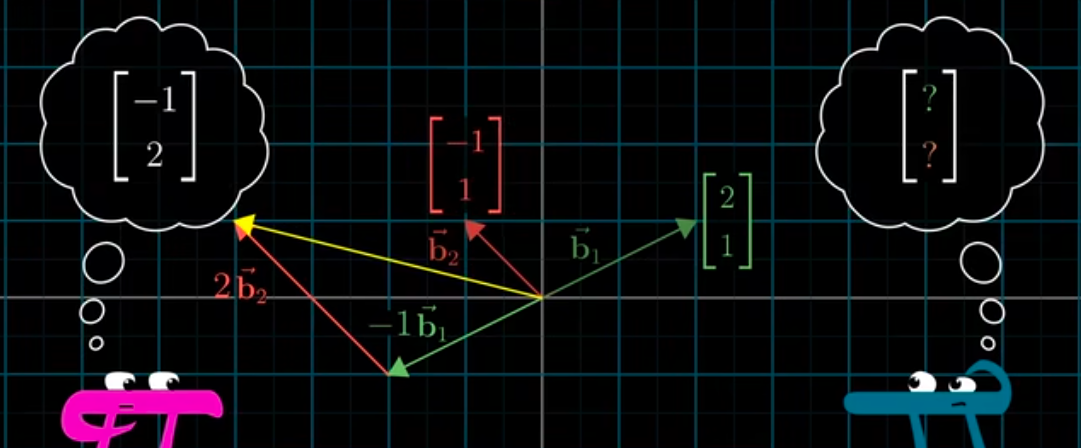
就可以得到我們的坐標系下的坐標了:
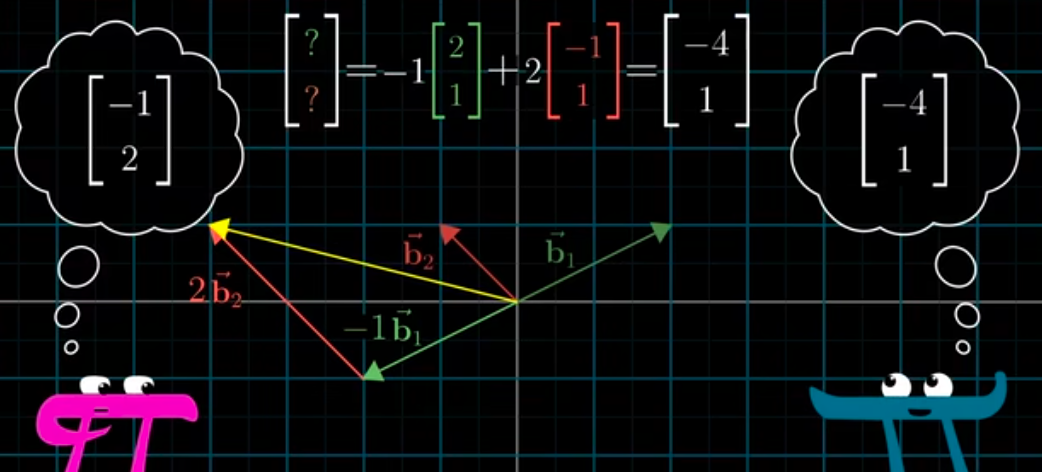 線性變換的一個重要特性在于,變換后的向量仍舊是相同的線性組合,不過使用的是新的基向量。
線性變換的一個重要特性在于,變換后的向量仍舊是相同的線性組合,不過使用的是新的基向量。
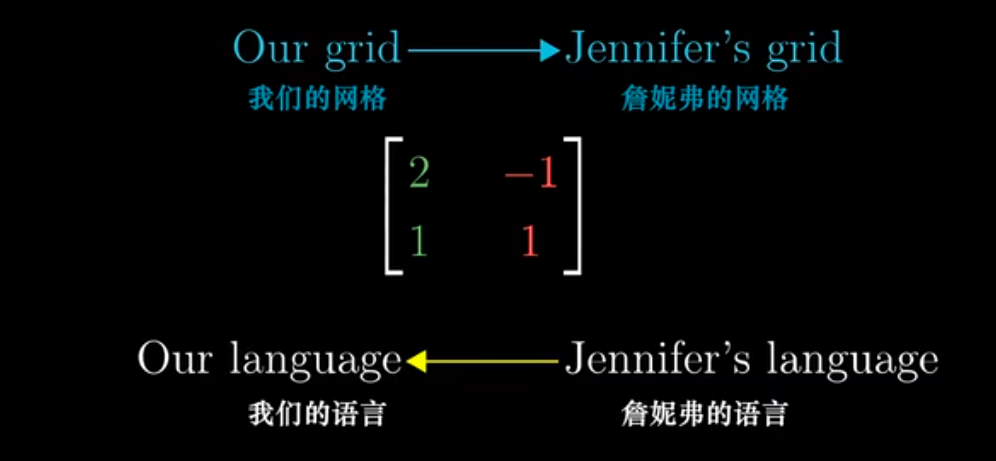
用數學語言表示就是:
舉例說明,在原坐標系下的向量(2,1),經過剪切矩陣的變換后,以剪切矩陣的列向量為新基(這也是原坐標軸轉移到的地方),其坐標仍然是(2,1),只不過是基于新的基向量,從原坐標系來看,其坐標是(3,1)。 兩個坐標誰是對的呢? 答案是相對于各自的基向量,兩個坐標都對,兩者描述同一向量,只是參考系不同。所以,當我們討論坐標的時候,一定要事先問清楚,相對的是哪個基,拋開基向量討論坐標位置是沒有意義的,就像“蘋果”與 “apple”指代同一物體,但符號不同,它們的基就是不同的文明背景。
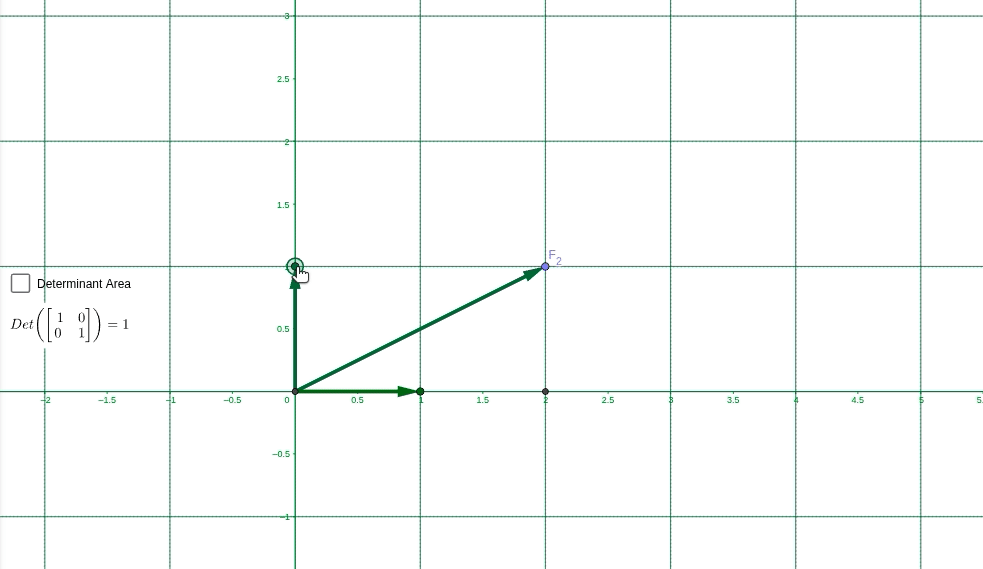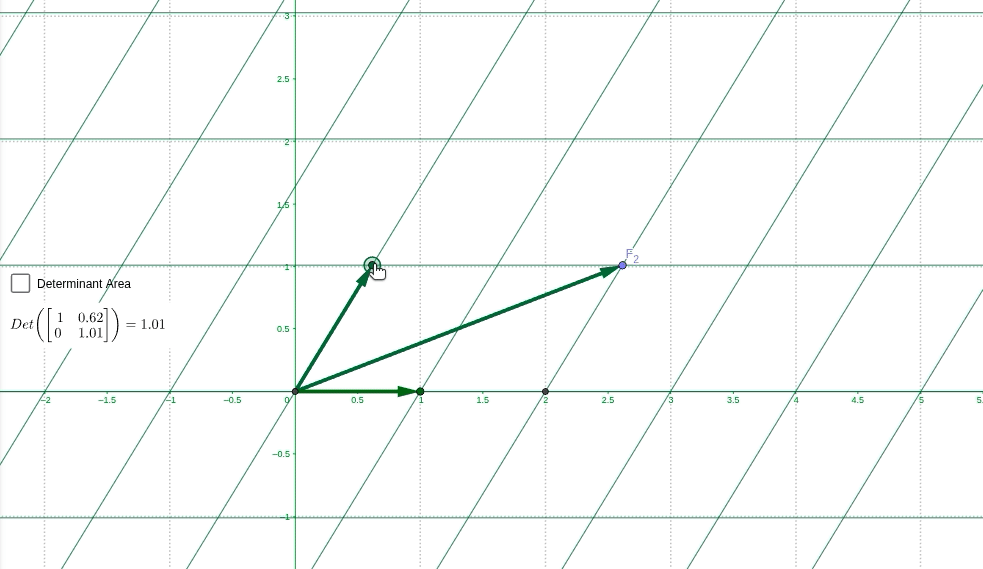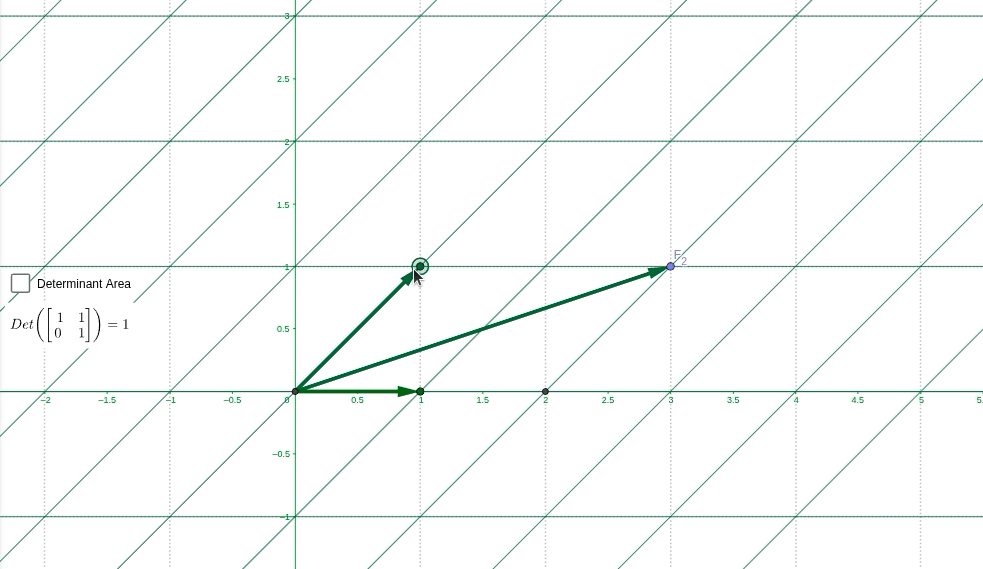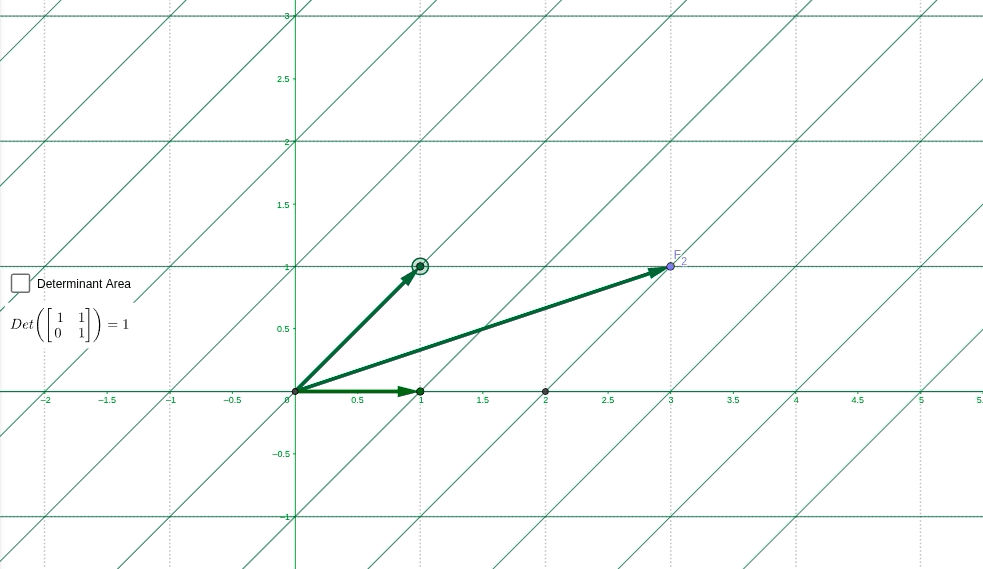
垂直的絕對性
前面提到了可以將非正交的基看成是(1,0)和(0,1)而不會產生自洽問題,但是線性代數中明明學過,兩個垂直的向量其內積為0,內積的計算方式是兩個向量的坐標點乘,所以如果新的非正交坐標系可以看作是(1,0)和(0,1),其坐標點積為0,推導出內積為0,說明兩個坐標系垂直,但是前提明明是新基非正交的呀?矛盾。

其實,上面的邏輯鏈條中存在一個問題,在非正交基下,內積不再等于兩個向量的坐標點乘,也就是說,在任何坐標系下,內積為0確實表示向量互相垂直,但是在非正交基下,內積就不能通過坐標的點積進行計算了,點積計算的結果和基的選擇有直接關系。
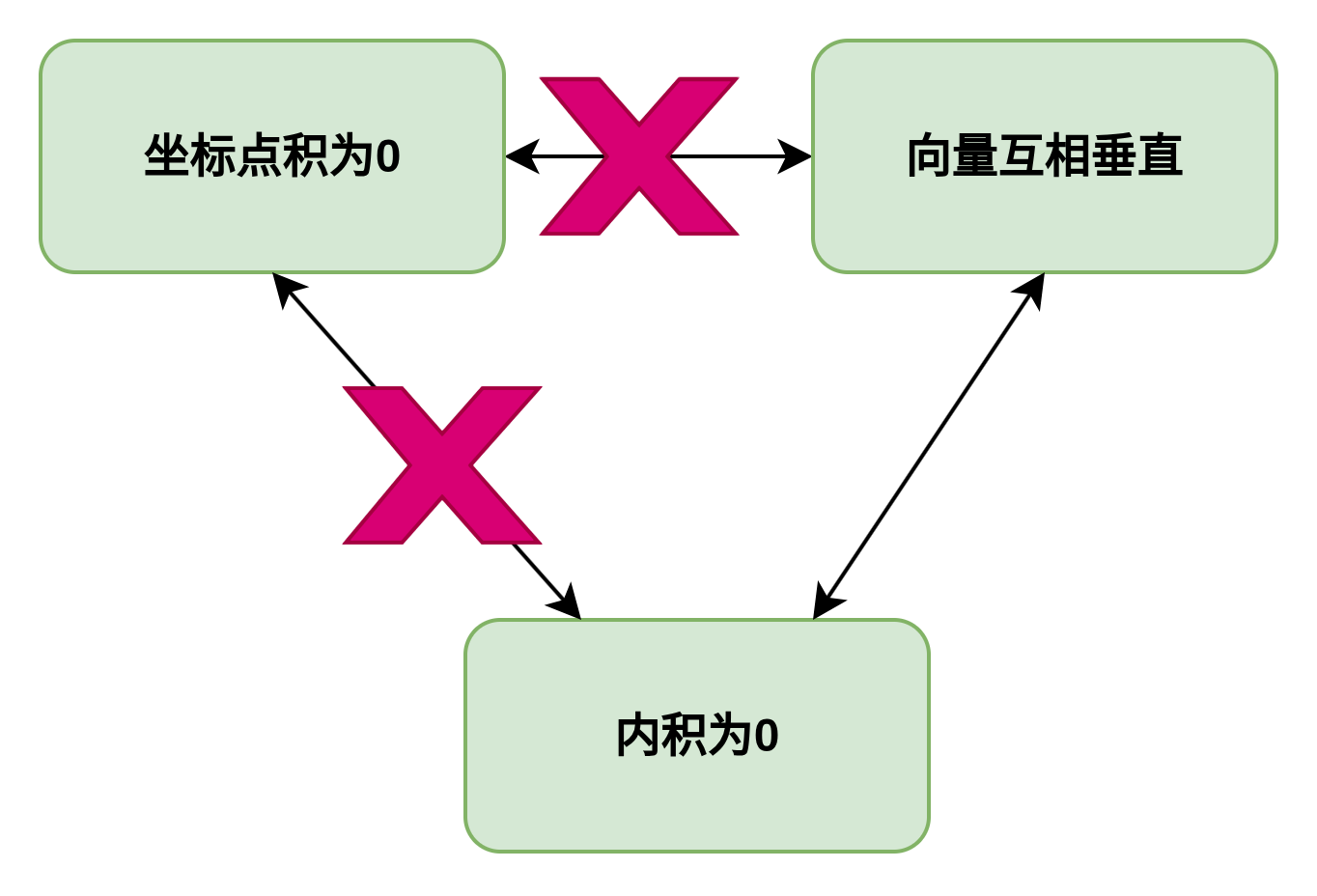
在包括非正交形式的任何基變換下,垂直都是絕對的,垂直由真實內積??u,v?=0定義,在任何坐標系下對應90°夾角。
實際上,內積的完整計算公式是:
其中G是度規矩陣,在標準正交基下,G是單位矩陣,所以可以內積計算公式蛻化為線性代數課本上介紹的:
而在非正較基下,其空間中的兩個向量的
內積計算公式為:
為了計算G,我們先將非標準坐標系下的向量轉換回原正交坐標系:
因為原坐標系正交,可以直接用坐標點乘得到真實內積:
代入:
所以,最終得到度規矩陣G的表達式如下,可以看到其是一個對稱矩陣:
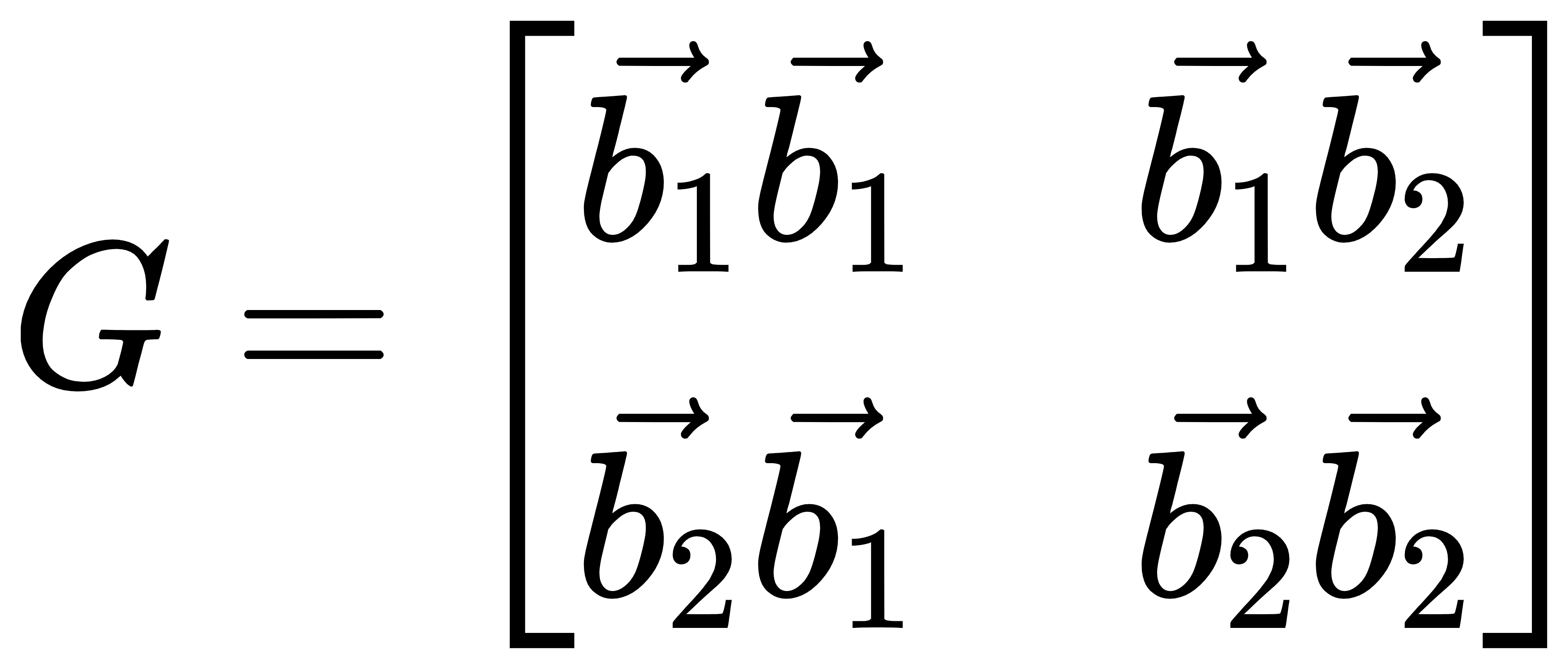
考慮到非正交坐標系,則任意向量的長度公式變為:
在非正交基下,坐標點積為零的向量不一定實際垂直。其實際夾角由度量矩陣G修正:
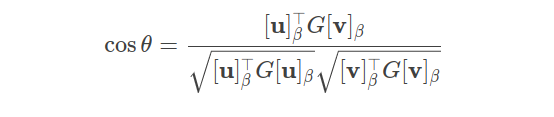
舉例說明
設定:
地球人:標準正交基,點P的坐標(3,4).
外星人:非正交基,從地球人的角度看,其基坐標為:
但是對于外星人來說,他們同樣認為自己的基是(1,0)和(0,1),和地球人無異。地球人根據基變換規則,計算出同樣的P點在外星人的坐標系下的坐標為:

地球人計算P點到原點的坐標,根據勾股定理:
在小尺度下,外星人沒有意識到自己使用的基是非正交的,如果其同樣知道了勾股定理,則其計算兩點間距離的方式和地球人一樣,根據勾股定理:
同樣空間中兩點間的距離,外星人計算出的結果和地球人不同!兩個文明之間開始意識到哪里出了問題。
問題解決
矛盾出現后,雙方可能通過以下方式發現坐標系差異,交換基的信息,地球人立刻就會發現外星人使用的基不是正交的。外星人意識到這一點后,立刻根據自己的基向量在地球人的標準坐標系下的坐標,計算出度規矩陣G:
外星人根據度規矩陣重新計算向量內積得到距離,應用內積公式:
進而得到和地球人同樣的P點距離原點的距離值是5,兩個文明最終就距離問題達成了一致。這里面的關鍵在于認識到度量矩陣G的存在。
總結
宇宙沒有義務滿足人類對直角的審美,正交性和平直性只是空間的局部近似,即使空間在大尺度上是彎曲的,但是對于活動范圍有限的生命體來說,其認識到的空間是"局部可微“的,可以近似看成是平直的歐式空間,所以發展歐式幾何來度量這個空間是文明自然而然的選擇,生命并不能天然的覺察到自己所在的空間是彎曲的(可能生活在黑洞或者中子星附近的文明能夠直觀感受到非正交坐標系和非平直空間),除非像前面的例子一樣,遇到不同文明的碰撞,或者產生出像愛因斯坦那樣的天才,對人類的空間觀念進行徹底的革新。
有限尺度生命體必然首先發展歐氏幾何,因其與局域測量一致,內部突破需愛因斯坦式天才,將思想實驗與數學重構結合,或者外部文明的輸入。實際上,人類是通過自我突破完成上述認知的,人類已經發現我們地球所在的宇宙空間,其度規矩陣G并非單位矩陣,這實際上說明,我們人類才是例子中的那個外星文明。
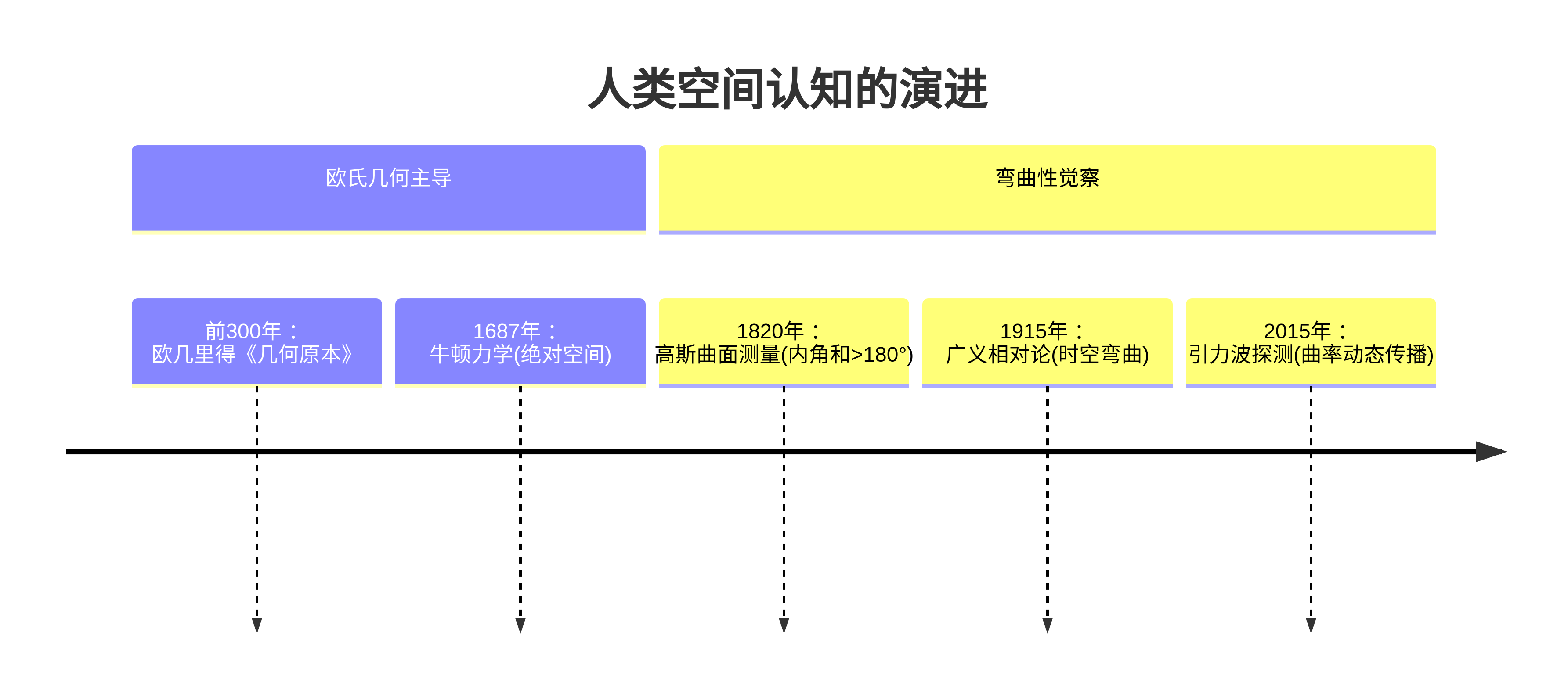
這印證了,從局部歐氏到全局彎曲的認知躍遷,需千年量級的科學積累。

![《P4180 [BJWC2010] 嚴格次小生成樹》](http://pic.xiahunao.cn/《P4180 [BJWC2010] 嚴格次小生成樹》)




)





 詳細版)




)

