Fabonacci 數列，也就是”兔子數列“，

如果第一項為0的話，就是，

0，1，1，2，3，5，8，13，21，34，55，89……

第一項不是0也可以，

1，1，2，3，5，8，13，21，34，55，89……

它是一個無限長數列。

它的特點是，除了前兩項0和1之外，或者不考慮0，除了前兩項1和1之外，后面的每一項都是其前兩項的和。其通項形式為，F[n]=F[n-1]+F[n-2](n>=2,F[0]=1,F[1]=1)

百度百科上是這么寫的：

在數學歷史上，歐洲黑暗時期過后，第一位有影響的數學家是斐波那契(L．Fibonacci，1170一1250)。他早年就隨其父在北非師從阿拉伯人學習算學，后又游歷地中海沿岸諸國，回意大利后寫成《算經》，也翻譯成《算盤書》。這部很有名的著作主要是一些源自古代中國、印度和希臘的數學問題的匯集，內容涉及整數和分數算法、開方法、二次和三次方程以及不定方程。特別是，在1228年的《算經》修訂版上載有如下“兔子問題”：?

“斐波那契數列”是什么？用筆畫出松果的走向，有趣的現象發生了

如果每對兔子（一雄一雌）每月能生殖一對小兔子（也是一雄一雌，下同），每對兔子第一個月沒有生殖能力，但從第二個月以后便能每月生一對小兔子.假定這些兔子都沒有死亡現象，那么從第一對剛出生的兔子開始，12 個月以后會有多少對兔子呢？ 解釋說明為：一個月：只有一對兔子；第二個月：仍然只有一對兔子；第三個月：這對兔子生了一對小兔子， 共有 1+1=2 對兔子.第四個月：最初的一對兔子又生一對兔 子，共有 2+1=3 對兔子.則由第一個月到第十二個月兔子的 對數分別是,0，1，1，2，3，5，8，13，21，34，55，89，144， ……，后人為了紀念提出兔子繁殖問題的斐波納契， 將這個兔子數列稱為斐波那契數列， 即把,0，1，1，2，3，5，8，13，21，34……這樣的數列稱為斐波那契數列。?

這里需要特別注意的是，數列中每一項的數值的單位是“對”也就是“一雄一雌”兩只兔子，而不是一只兔子。這一點特別容易被忽視。

隨著數列長度的增加，前后兩項的比越來越接近于黃金分割率0.618034的倒數1.618034.

這個倒數是方程，

x(x-1)=0

的正根，負根的絕對值為黃金分割率。

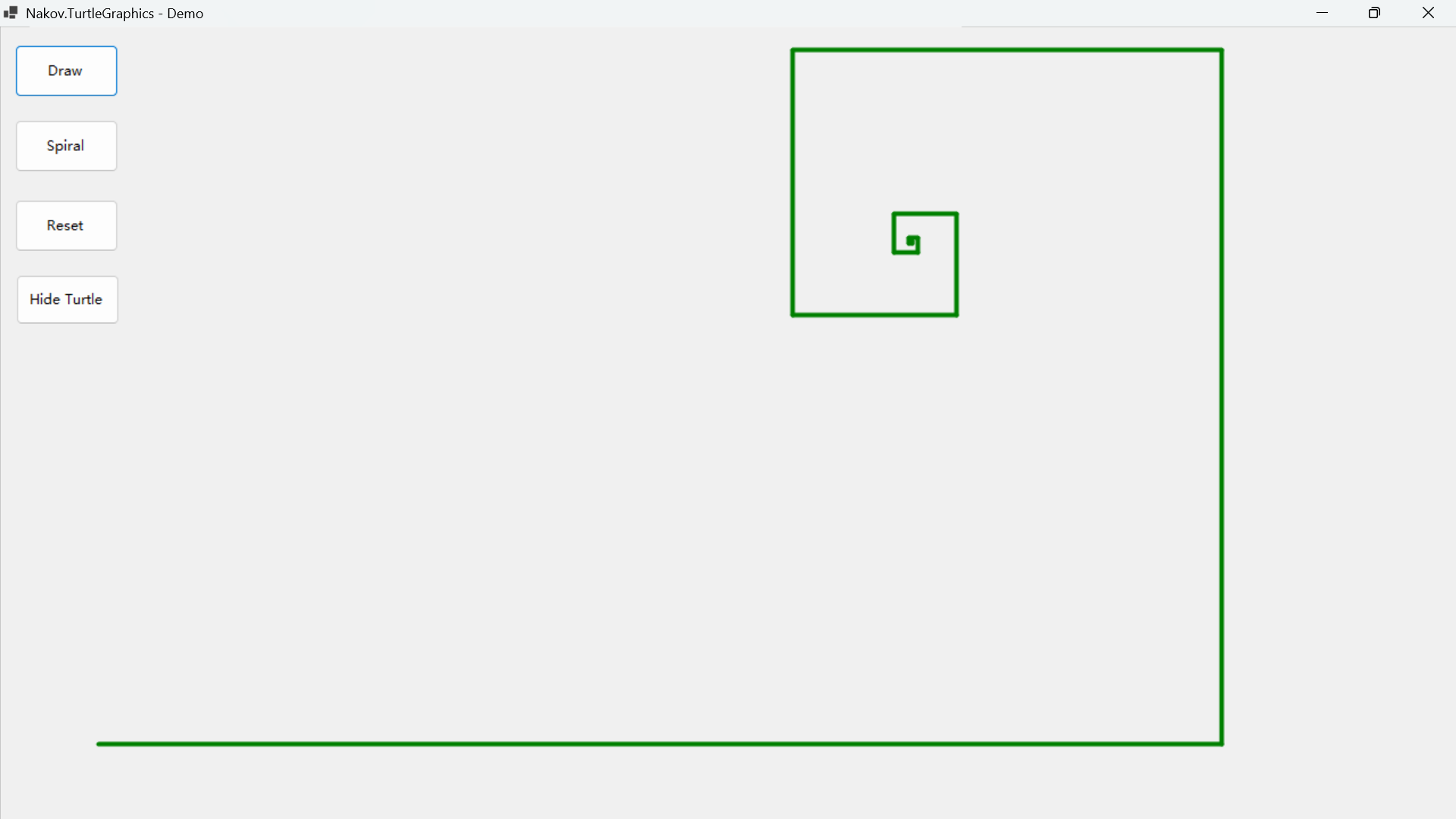
C#上有一個很好用的繪圖庫，Nakov.TurtleGraphics。

它其實就是C#版本的Turtle(Python)，也就是早年的LOGO語言的海龜繪圖。

這件事其實就是為了畫出直角轉彎的斐波那契數列，而不是為了介紹繪圖工具。

    private void ButtonDraw_Click(object sender, EventArgs e){// Assign a delay to visualize the drawing processTurtle.Delay = 0;Turtle.PenSize = 4;Turtle.ShowTurtle = false;// Draw a equilateral triangleTurtle.PenColor = Color.Green;Turtle.PenUp();Turtle.Forward(160);Turtle.Rotate(90);Turtle.Forward(160);Turtle.Rotate(-90);Turtle.PenDown();int length;int an_1 = 1, an_2 = 0;for (int i = 0; i < 16; i++){length = an_1 + an_2;Turtle.Forward(length);Turtle.Rotate(90);//Debug.WriteLine(length);an_1 = an_2;an_2 = length;}}

Github:?https://github.com/yyl-20020115/TurtleGraphics.NET.git?