【LeetCode Solutions】LeetCode 熱題 100 題解（36 ~ 40）

二叉樹 - LeetCode 94. 二叉樹的中序遍歷（簡單）
二叉樹 - LeetCode 104. 二叉樹的最大深度（簡單）
二叉樹 - LeetCode 226. 翻轉二叉樹（簡單）
二叉樹 - LeetCode 101. 對稱二叉樹（簡單）
二叉樹 - LeetCode 543. 二叉樹的直徑（簡單）

二叉樹 - LeetCode 94. 二叉樹的中序遍歷（簡單）

【題目描述】

給定一個二叉樹的根節點 root，返回它的中序遍歷。

【示例 1】

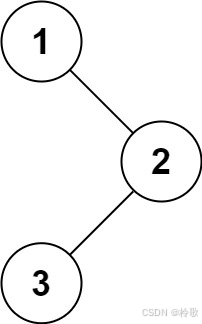
在這里插入圖片描述

輸入：root = [1,null,2,3]
輸出：[1,3,2]

【示例 2】

輸入：root = []
輸出：[]

【示例 3】

輸入：root = [1]
輸出：[1]

【提示】

樹中節點數目在范圍 $[0, 100]$ 內
$? 100 <= N o d e . v a l <= 100$

進階：遞歸算法很簡單，你可以通過迭代算法完成嗎？

【分析】

遞歸遍歷二叉樹非常簡單，不理解的可以看樹和圖的遍歷方式詳解：【UCB CS 61B SP24】Lecture 22 & 23: Tree and Graph Traversals, DFS, BFS。

本題的 Tips 中提到嘗試用迭代算法完成，那么分析一下如何不用遞歸實現中序遍歷。

對于每個節點，如果其左子樹存在，就需要先遍歷左子樹，但是當前點也不能扔掉，因為遍歷完左子樹還要回來遍歷當前節點，因此如果當前節點有左子樹就先將當前點壓入棧中。

如果當前節點的左子樹已經遍歷完了，就可以遍歷自身了，遍歷完就可以出棧，如果有右子樹，那么就對右子樹繼續執行相同的操作遍歷，如果沒有右子樹就可以出棧下一個節點，也就是當前節點的父節點。

【代碼】

【遞歸方法】

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> res;vector<int> inorderTraversal(TreeNode* root) {if (!root) return res;if(root->left) inorderTraversal(root->left);res.push_back(root->val);if (root->right) inorderTraversal(root->right);return res;}
};

【迭代方法】

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> inorderTraversal(TreeNode* root) {vector<int> res;stack<TreeNode*> stk;while (root || stk.size()) {  // 當前節點不為空或棧不為空時循環操作while (root) {  // 一直走到沒有左子樹為止stk.push(root);root = root->left;}root = stk.top();  // root 為空時說明棧頂元素可以被遍歷了stk.pop();res.push_back(root->val);root = root->right;  // 如果沒有右子樹 root 就為空，下一次出棧的就是 root 的父節點}return res;}
};

二叉樹 - LeetCode 104. 二叉樹的最大深度（簡單）

【題目描述】

給定一個二叉樹 root，返回其最大深度。

二叉樹的最大深度是指從根節點到最遠葉子節點的最長路徑上的節點數。

【示例 1】

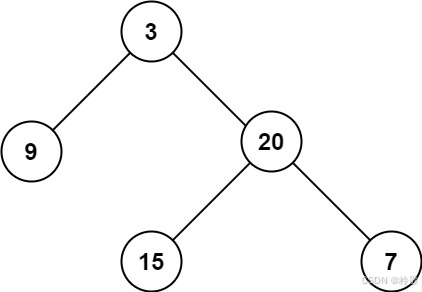
在這里插入圖片描述

輸入：root = [3,9,20,null,null,15,7]
輸出：3

【示例 2】

輸入：root = [1,null,2]
輸出：2

【提示】

樹中節點的數量在 $0, 10^4]$ 區間內。
$? 100 <= N o d e . v a l <= 100$

【分析】

用 BFS 也就是類似前兩題的做法能夠求出層數，也可以直接用遞歸求解，從根節點往下遞歸求解每個節點的高度，到空節點了高度就為 0，否則當前節點的高度就是左子樹與右子樹中的最大高度加一（當前節點的高度比子樹多 1）。

【代碼】

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int maxDepth(TreeNode* root) {  // 返回 root 的最大高度if (!root) return 0;return max(maxDepth(root->left), maxDepth(root->right)) + 1;}
};

二叉樹 - LeetCode 226. 翻轉二叉樹（簡單）

【題目描述】

給你一棵二叉樹的根節點 root，翻轉這棵二叉樹，并返回其根節點。

【示例 1】

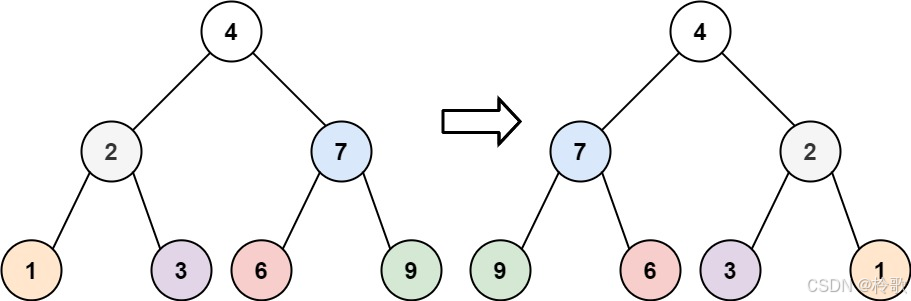
在這里插入圖片描述

輸入：root = [4,2,7,1,3,6,9]
輸出：[4,7,2,9,6,3,1]

【示例 2】

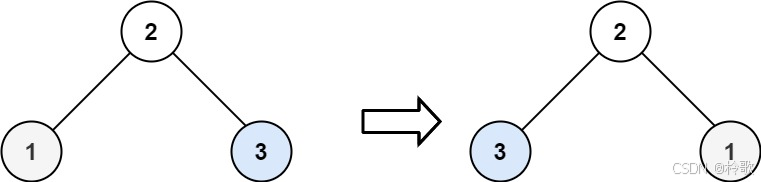
在這里插入圖片描述

輸入：root = [2,1,3]
輸出：[2,3,1]

【示例 3】

輸入：root = []
輸出：[]

【提示】

樹中節點數目范圍在 $[0, 100]$ 內
$? 100 <= N o d e . v a l <= 100$

【分析】

從根節點開始遞歸地處理每個結點，將每個結點的左右子樹交換一下即可。

【代碼】

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* invertTree(TreeNode* root) {if (!root) return nullptr;swap(root->left, root->right);invertTree(root->left);invertTree(root->right);return root;}
};

二叉樹 - LeetCode 101. 對稱二叉樹（簡單）

【題目描述】

給你一個二叉樹的根節點 root，檢查它是否軸對稱。

【示例 1】

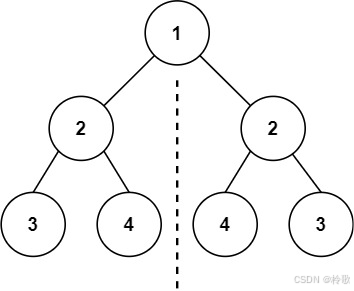
在這里插入圖片描述

輸入：root = [1,2,2,3,4,4,3]
輸出：true

【示例 2】

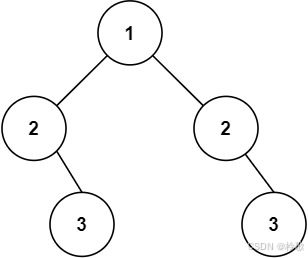
在這里插入圖片描述

輸入：root = [1,2,2,null,3,null,3]
輸出：false

【提示】

樹中節點數目在范圍 $[1, 1000]$ 內
$? 100 <= N o d e . v a l <= 100$

進階：你可以運用遞歸和迭代兩種方法解決這個問題嗎？

【分析】

對稱的樹具有以下屬性之一：

左右子節點均為空；
左右子節點的值相同，且左子節點的左子樹與右子節點的右子樹相同，左子節點的右子樹與右子節點的左子樹相同。

因此我們可以遞歸判斷左右子樹是否對稱。

題目提到用遞歸和迭代實現，那么如何用迭代實現？

可以用隊列維護對稱的相對關系，首先將根節點的左右子節點入隊，然后不斷循環每次從隊列中取兩個節點，判斷這兩個節點是否對稱，然后將其中一個節點的左/右子節點與另一個節點的右/左子節點對應成兩組分別加入到隊列中，如果隊列為空遍歷完整棵樹還沒發現非對稱的節點說明整棵樹就是對稱的。

【代碼】

【遞歸方法】

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool isSymmetric(TreeNode* root) {return dfs(root->left, root->right);}bool dfs(TreeNode* l, TreeNode* r) {if (!l && !r) return true;  // 兩個節點均為空if (!l || !r || l->val != r->val) return false;  // 只有一個節點為空或兩個節點值不同return dfs(l->left, r->right) && dfs(l->right, r->left);  // 左節點的左/右子樹要和右節點的右/左子樹對稱}
};

【迭代方法】

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool isSymmetric(TreeNode* root) {queue<TreeNode*> Q;Q.push(root->left), Q.push(root->right);while (!Q.empty()) {auto p = Q.front(); Q.pop();auto q = Q.front(); Q.pop();if (!p && !q) continue;if (!p || !q || p->val != q->val) return false;  // 不對稱Q.push(p->left), Q.push(q->right);  // p 的左子節點需要和 q 的右子節點對稱Q.push(p->right), Q.push(q->left);  // p 的右子節點需要和 q 的左子節點對稱}return true;  // 全遍歷完了說明樹是對稱的}
};

二叉樹 - LeetCode 543. 二叉樹的直徑（簡單）

【題目描述】

給你一棵二叉樹的根節點，返回該樹的直徑。

二叉樹的直徑是指樹中任意兩個節點之間最長路徑的長度。這條路徑可能經過也可能不經過根節點 root。

兩節點之間路徑的長度由它們之間邊數表示。

【示例 1】

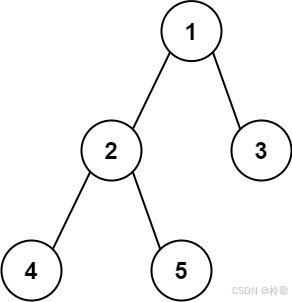
在這里插入圖片描述

輸入：root = [1,2,3,4,5]
輸出：3
解釋：3 ，取路徑 [4,2,1,3] 或 [5,2,1,3] 的長度。

【示例 2】

輸入：root = [1,2]
輸出：1

【提示】

樹中節點數目在范圍 $1, 10^4]$ 內
$? 100 <= N o d e . v a l <= 100$

【分析】

我們遞歸枚舉每個點作為路徑的最高點，那么這條路徑的長度為該結點往左子樹走的最大長度加上往右子樹走的最大長度，因此可以在遞歸的時候維護每個結點往下走到葉子結點的最大長度，這樣就能快速獲得當前結點左右子樹往下走的最大長度。

如果是多叉樹求樹的直徑有通用解法（求圖的最長路徑），首先任選一個點作為根結點，通過 DFS 找到最遠的結點，然后再將其作為根節點，通過 DFS 找到最遠的點，這段距離就是最長路徑。

【代碼】

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int res;int dfs(TreeNode* root) {  // 返回從 root 往下走的最長長度if (!root) return 0;int l = dfs(root->left), r = dfs(root->right);res = max(res, l + r);return max(l, r) + 1;}int diameterOfBinaryTree(TreeNode* root) {dfs(root);return res;}
};