為什么需要批量規范化層呢？

讓我們來回顧一下訓練神經網絡時出現的一些實際挑戰：

• 首先，數據預處理的方式通常會對最終結果產生巨大影響。 回想一下我們應用多層感知機來預測房價的例子。使用真實數據時，我們的第一步是標準化輸入特征，使其平均值為0，方差為1。 直觀地說，這種標準化可以很好地與我們的優化器配合使用，因為它可以將參數的量級進行統一。

• 第二，對于典型的多層感知機或卷積神經網絡，當我們訓練時，中間層中的變量（例如，多層感知機中的仿射變換輸出）可能具有更廣的變化范圍：不論是沿著從輸入到輸出的層，跨同一層中的單元，或是隨著時間的推移，模型參數的隨著訓練更新變幻莫測。 批量規范化的發明者非正式地假設，這些變量分布中的這種偏移可能會阻礙網絡的收斂。 直觀地說，我們可能會猜想，如果一個層的可變值是另一層的100倍，這可能需要對學習率進行補償調整。

• 第三，更深層的網絡很復雜，容易過擬合。 這意味著正則化變得更加重要。

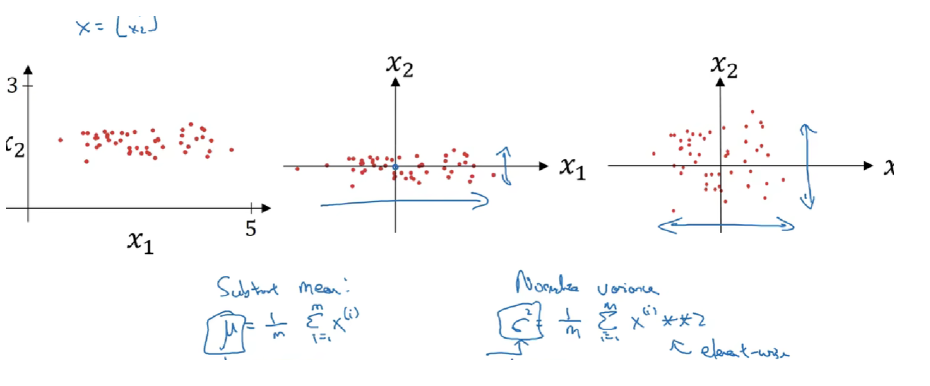
批量規范化應用于單個可選層（也可以應用到所有層），其原理如下：

在每次訓練迭代中，我們首先規范化輸入，即通過減去其均值并除以其標準差，其中兩者均基于當前小批量處理。 接下來，我們應用比例系數和比例偏移。 正是由于這個基于批量統計的標準化，才有了批量規范化的名稱。

• BatchNorm 在 一個 batch 的同一通道 內做歸一化

• LayerNorm 在 每條樣本的 所有通道/特征 內做歸一化

作用：把輸入分布強行壓成 零均值、單位方差，減輕 Internal Covariate Shift 內部協變量偏移，使優化曲面更平滑，從而讓梯度更穩定、訓練更快、更易收斂到較優的泛化解。

計算例子

下面用 3×4 的 RGB 小批次張量舉例，并給出計算過程與差異對照：

數據形狀約定：設輸入 x 形狀為 (B, C, H, W) = (2, 3, 2, 2)：

1. 2 張圖片

2. 3 個通道 (R, G, B)

3. 每通道 2×2 像素

把每張圖片展平后，張量變成：

batch0-0R: [[1, 3], [5, 7]]    → 4 個標量 1 3 5 7G: [[2, 4], [6, 8]]    → 2 4 6 8B: [[0, 2], [4, 6]]    → 0 2 4 6batch0-1R: [[2, 4], [6, 8]]G: [[3, 5], [7, 9]]B: [[1, 3], [5, 7]]

BatchNorm 的計算：BN是在同一個batch中不同樣本之間的同一位置的神經元之間進行歸一化。

• 歸一化維度：在 (B, H, W) 三個維度上求均值/方差，每個通道一組統計量。

• 以 R 通道為例： 共有 2×2×2 = 8 個像素值：{1, 3, 5, 7, 2, 4, 6, 8}

  • μ_R = (1+3+5+7+2+4+6+8)/8 = 4.5

  • σ2_R = 平均((x?4.5)2) = 5.25

• 歸一化后每個像素先做 (x?μ)/√(σ2+ε)，再進行 γ·x + β 的仿射。 G、B 通道同理，各自獨立擁有一組 μ、σ、γ、β。

• 參數：每個通道一對 (γ, β)，共 3×2 = 6 個可學習標量。

• 推理階段：用滑動平均保存的全局 μ、σ，不再依賴 batch。

LayerNorm 的計算：LN是在同一個樣本中不同神經元之間進行歸一化。

• 歸一化維度：在 (C, H, W) 三個維度上求均值/方差，每條樣本一組統計量。

• 以 batch-0 為例： 把 3×2×2 = 12 個數拉成一條向量： {1, 3, 5, 7, 2, 4, 6, 8, 0, 2, 4, 6}

  • μ = 4.0

  • σ2 = 平均((x?4)2) = 5.0

• 歸一化后再用 該樣本獨有 的 γ、β 做仿射。 batch-1 同理，用 batch-1 自己的 12 個數重新算 μ、σ。

• 參數：每條樣本一對 (γ, β)，可共享或不共享，與 BatchNorm 不同。

為什么有效？

• 輸入：手寫數字灰度圖，只保留 2 個像素 → 輸入 x 形狀 (batch, 2)。

• 網絡：2 層線性 y = W? ReLU(W?x)。

• 任務：二分類 0/1，用 Sigmoid + BCE 損失。

• 假設 batch = 4，像素值如下（故意把范圍拉大）：

  x = [[200, 190],[10,  5],[180, 170],[8,   4]]

• 真實標簽 y = [0,? 1,? 0,? 1]

沒有歸一化時（裸網絡）

• 第一層輸出 z? = W?x，假設 W? 隨機初始化后， z? 的均值≈180，方差≈6000。

• 經過 ReLU 后，大多數值落在 0 或 >100 的區間 → 梯度在反向傳播時： – 很大值那一端 → 梯度爆炸； – 很多 0 → 梯度消失。 結果：Loss 震蕩劇烈，訓練 10 個 epoch 仍降不下來。

加上 BatchNorm（放在第一層之后）：

1. 計算 batch 內每個通道的均值 μ、方差 σ2：

   • μ? = (200+10+180+8)/4 = 99.5

   • μ? = (190+5+170+4)/4 = 92.25

2. 歸一化：

   • ?? = (z? ? μ?)/√(σ?2+ε)

   • ?? = (z? ? μ?)/√(σ?2+ε)

3. 現在所有值縮放到 ≈[-1,1] 區間。

4. 再乘可學習 γ、β 做仿射，保持表達能力。

5. 效果：

   • 第一層輸出方差≈1，ReLU 后的分布不再極端。

   • 反向傳播時梯度大小穩定，loss 單調下降，3 個 epoch 就收斂。

加上 LayerNorm（放在第一層之后）

• 對每條樣本的所有特征一起算 μ、σ2：

  • 樣本 0：μ = (200+190)/2 = 195

  • 樣本 1：μ = (10+5)/2 = 7.5

  • …………

• 每條樣本內部做 (x?μ)/σ，再 γ、β。

  • 效果：

    • 即使 batch 大小變成 1 也能用（LN 不依賴 batch）。

    • 輸入尺度被拉齊，梯度同樣穩定，收斂速度與 BN 相近。

因此：

• 在 CNN 里用 BatchNorm，你會看到“所有圖片的 R 通道一起歸一化”；

• 在 Transformer 里用 LayerNorm，你會看到“每個 token 的所有維一起歸一化”。