語言模型
語言(人說的話)+模型(完成某個任務)
任務:
- 概率評估任務:在兩句話中,判斷哪句話出現的概率大(哪句話在自然語言中更合理)
- 生成任務:預測詞語,我明天要
____
統計語言模型
用統計的方法解決上述的兩個任務
核心思想
給定一個詞序列,計算該序列出現的概率
比如句子:“判斷這個詞的詞性”,分詞得到"判斷",“這個”,“詞”,“的”,“詞性”
這句話是有順序的(是一個序列),怎么理解(?)
就是自然語言我們所說的語序
條件概率鏈式法則
用于解決第一個任務
$$
統計語言模型的核心是計算一個句子 P(w_1,w_2,…,w_n) 的聯合概率,即一句話出現的概率(w_i就是單個詞)\
P(w_1,w_2,\cdots,w_n) = P(w_1)\cdot P(w_2|w_1)\cdots P(w_n|w_1,w_2,\cdots,w_{n-1}) = \prod_{i}P(w_i | w_1,w_2,\cdots,w_{i-1})\
$$
(?)理解:求出每個詞wi的概率,然后連乘,就是這個句子的概率;
為什么是條件概率(?)
因為句子是一個序列,計算當前詞的概率需要在前面的詞已經確定的前提下(每個詞是基于上下文的)
詞庫/詞典
解決第二個任務:生成任務 我明天要____
令要生成的詞為wnext,其概率為(1)P(wnext∣"我","明天","要")
令要生成的詞為w_{next},其概率為\\
(1) P(w_{next} | "我","明天","要")
令要生成的詞為wnext?,其概率為(1)P(wnext?∣"我","明天","要")
思想
- 建立一個詞典V,把所有詞都裝入V
- 把V中每個詞都進行(1)式計算
缺點
- 計算太復雜了
- 詞典很大,要匹配很多次計算
- 句子很復雜,分詞后非常長,計算也很復雜
前面沒有給出這個情境下的條件概率怎么計算
P(wnext∣"我","明天","要")=count(wnext,"我","明天","要")count("我","明天","要")count():表示某個詞或詞序列在語料庫中出現的次數eg:我?明天?要?去?學校我?明天?要?去?玩我?明天?要?睡覺我?明天?要?上班我?明天?要?吃飯count("我","明天","要")=5????我?明天?要?這三個詞同時出現的次數
P(w_{next} | "我","明天","要") = \frac{count(w_{next},"我","明天","要")}{count("我","明天","要")} \\
count(): 表示某個詞或詞序列在語料庫中出現的次數\\
eg:\\
我 \ 明天\ 要\ 去\ 學校\\
我\ 明天\ 要\ 去\ 玩\\
我 \ 明天\ 要 \ 睡覺\\
我 \ 明天\ 要 \ 上班\\
我 \ 明天 \ 要\ 吃飯\\
count("我","明天","要")=5 \ \ \ -我\ 明天\ 要\ 這三個詞同時出現的次數
P(wnext?∣"我","明天","要")=count("我","明天","要")count(wnext?,"我","明天","要")?count():表示某個詞或詞序列在語料庫中出現的次數eg:我?明天?要?去?學校我?明天?要?去?玩我?明天?要?睡覺我?明天?要?上班我?明天?要?吃飯count("我","明天","要")=5????我?明天?要?這三個詞同時出現的次數
這count()怎么算的(?)
在語料庫中詞序列出現次數,比如count(“我”,“明天”,“要”)要把"我","明天","要"當成序列,再找出現次數,而不是分開每個詞尋找
n-gram模型/n元統計語言模型
n-gram模型用于預測一個詞在給定前n-1個詞的情況下出現的概率
引入
比如對于這樣一個生成任務:
判斷這個詞的___
wnext="詞性","火星"最原始的式子:P(wnext∣"判斷","這個","詞","的")但是也可以這樣:P(wnext∣這個","詞","的")還可以這樣:P(wnext∣"詞","的")三個式子都能達到選出最佳生成詞語的作用,但是很顯然最后一個式子要更加高效
w_next = {"詞性","火星"}\\
最原始的式子:P(w_{next}|"判斷","這個","詞","的")\\
但是也可以這樣:P(w_{next}|這個","詞","的")\\
還可以這樣:P(w_{next}|"詞","的")\\
三個式子都能達到選出最佳生成詞語的作用,但是很顯然最后一個式子要更加高效
wn?ext="詞性","火星"最原始的式子:P(wnext?∣"判斷","這個","詞","的")但是也可以這樣:P(wnext?∣這個","詞","的")還可以這樣:P(wnext?∣"詞","的")三個式子都能達到選出最佳生成詞語的作用,但是很顯然最后一個式子要更加高效
定義
n-gram是指連續的n個詞構成的序列。n元模型(n-gram model)是基于前 n?1 個詞來預測第 n 個詞的模型。- 常見的有:
- unigram(n=1):不考慮上下文,只統計詞頻。
- bigram(n=2):基于前一個詞預測下一個詞。
- trigram(n=3):基于前兩個詞預測下一個詞。
- 4-gram、5-gram 等:基于更多上下文。
最大似然估計MLE
P(wi∣wi?n+1,??,wi?1)=count(wi?n+1,??,wi?1,wi)count(wi?n+1,??,wi?1) P(w_i | w_{i-n+1},\cdots,w_{i-1}) = \frac{count(w_{i-n+1},\cdots,w_{i-1},w_i)}{count(w_{i-n+1},\cdots,w_{i-1})} P(wi?∣wi?n+1?,?,wi?1?)=count(wi?n+1?,?,wi?1?)count(wi?n+1?,?,wi?1?,wi?)?
缺點:
- 有現實意義的文本,通常會出現數據稀疏的情況;例如訓練時未出現的單詞,在測試時出現
- 這樣就會導致MLE的分子/分母為0,造成計算上的問題,我們需要引入一些平滑策略來避免0的出現
平滑策略
拉普拉斯平滑/加一平滑
P(wi∣wi?n+1,??,wi?1)=count(wi?n+1,??,wi?1,wi)+1count(wi?n+1,??,wi?1)+∣V∣∣V∣:詞庫大小 P(w_i | w_{i-n+1},\cdots,w_{i-1}) = \frac{count(w_{i-n+1},\cdots,w_{i-1},w_i)+1}{count(w_{i-n+1},\cdots,w_{i-1})+|V|}\\ |V|:詞庫大小 P(wi?∣wi?n+1?,?,wi?1?)=count(wi?n+1?,?,wi?1?)+∣V∣count(wi?n+1?,?,wi?1?,wi?)+1?∣V∣:詞庫大小
加k平滑
P(wi∣wi?n+1,??,wi?1)=count(wi?n+1,??,wi?1,wi)+kcount(wi?n+1,??,wi?1)+k∣V∣k:一個小于1的數,可以使用交叉驗證進行選擇∣V∣:詞庫大小 P(w_i | w_{i-n+1},\cdots,w_{i-1}) = \frac{count(w_{i-n+1},\cdots,w_{i-1},w_i)+k}{count(w_{i-n+1},\cdots,w_{i-1})+k|V|}\\ k:一個小于1的數,可以使用交叉驗證進行選擇\\ |V|:詞庫大小 P(wi?∣wi?n+1?,?,wi?1?)=count(wi?n+1?,?,wi?1?)+k∣V∣count(wi?n+1?,?,wi?1?,wi?)+k?k:一個小于1的數,可以使用交叉驗證進行選擇∣V∣:詞庫大小
Kneser-Ney 平滑
核心思想:一個詞是否可以作為多個上下文的結尾
PKN(wi∣context)=max?(count(wi,context),D,0)count(context)+λ(context)Pcont(wi)D:折扣因子λ:歸一化系數λ=D?N1+(context)C(context)N1+(Context):表示有多少個不同的wi使得C(wi,context)>0Pcont(wi):詞wi作為上下文結尾的概率Pcont(wi)=Cprefix(wi)∑w′Cprefix(w′)Cprefix(wi):有多少個不同的詞可以跟在wi前面組成bigram(n=2,根據前一個詞預測下一個詞)∑w′Cprefix(w′):所有詞的Cprefix總和
P_{KN}(w_i|context) = \frac{\max(count(w_i,context),D,0)}{count(context)}+\lambda(context)P_{cont}(w_i)\\
D:折扣因子\\
\lambda:歸一化系數\\
\lambda=\frac{D\cdot N_{1+}(context)}{C(context)}\\
N_{1+}(Context):表示有多少個不同的 w_i 使得 C(w_i,context)>0\\
P_{cont}(w_i):詞w_i作為上下文結尾的概率\\
P_{cont}(w_i) = \frac{C_{prefix}(w_i)}{\sum_{w'}C_{prefix}(w')}\\
C_{prefix}(w_i):有多少個不同的詞可以跟在w_i前面組成bigram(n=2,根據前一個詞預測下一個詞)\\
\sum_{w'}C_{prefix}(w'):所有詞的C_{prefix}總和\\
PKN?(wi?∣context)=count(context)max(count(wi?,context),D,0)?+λ(context)Pcont?(wi?)D:折扣因子λ:歸一化系數λ=C(context)D?N1+?(context)?N1+?(Context):表示有多少個不同的wi?使得C(wi?,context)>0Pcont?(wi?):詞wi?作為上下文結尾的概率Pcont?(wi?)=∑w′?Cprefix?(w′)Cprefix?(wi?)?Cprefix?(wi?):有多少個不同的詞可以跟在wi?前面組成bigram(n=2,根據前一個詞預測下一個詞)w′∑?Cprefix?(w′):所有詞的Cprefix?總和
例子:
我?明天?要?去?玩我?明天?要?去?學校生成bigram列表{(我,明天),(明天,要),(要,去),(去,玩)}{(我,明天),(明天,要),(要,去),(去,學校)}∑w′Cprefix(w′)=8Cprefix("明天")=2Pcont("明天")=28=14
我 \ 明天\ 要\ 去\ 玩\\
我\ 明天\ 要\ 去\ 學校\\
\\
生成bigram列表\\
\{(我,明天),(明天,要),(要,去),(去,玩)\}\\
\{(我,明天),(明天,要),(要,去),(去,學校)\}\\
\sum_{w'}C_{prefix}(w') = 8\\
C_{prefix}("明天")=2 \\
P_{cont}("明天")=\frac{2}{8}=\frac{1}{4}
我?明天?要?去?玩我?明天?要?去?學校生成bigram列表{(我,明天),(明天,要),(要,去),(去,玩)}{(我,明天),(明天,要),(要,去),(去,學校)}w′∑?Cprefix?(w′)=8Cprefix?("明天")=2Pcont?("明天")=82?=41?
問題(?)
公式的理解,對prefix一開始理解不太透徹,prefix就是:有多少個不同的詞可以跟在w_i前面組成bigram(n=2,根據前一個詞預測下一個詞)
神經網絡語言模型NNLM
這里提到NNLM是為了接下來引入Word2Vec
余弦相似度
cos(θ)=A?B∣∣A∣∣B∣∣=∑i=1nAiBi∑i=1nAi2∑i=1nBi2 cos(\theta) = \frac{A\cdot B}{||A||B||} = \frac{\sum_{i=1}^{n}A_iB_i}{\sqrt{\sum_{i=1}^{n}A_i^2}\sqrt{\sum_{i=1}^{n}B_i^2}} cos(θ)=∣∣A∣∣B∣∣A?B?=∑i=1n?Ai2??∑i=1n?Bi2??∑i=1n?Ai?Bi??
one-hot編碼表示詞的缺點

- 維度災難:假設有m=10000個詞
- 每個詞的向量長度都是m,整體大小太大,存儲開銷很大
- 不能表示出詞與詞之間的關系
- 例如Man和Woman關系比較近,Man和Apple關系比較遠,但是其實任取2個向量的內積都是0,也就是余弦相似度為0
流程
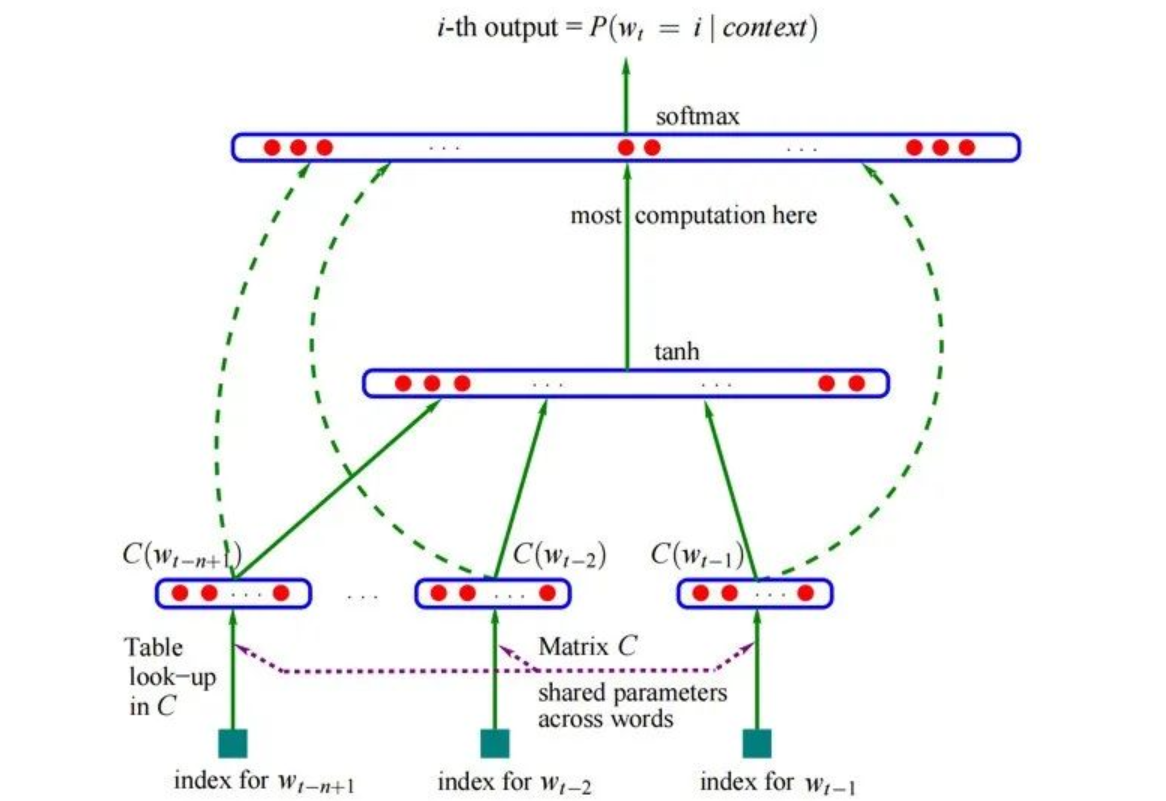
輸入層/Embedding層
先隨機生成矩陣Q,后面對Q進行訓練
wi?Q=ci詞矩陣C=[c1,c2,??,cn]w1×V:詞的one?hot編碼的向量QV×M:嵌入矩陣,類似于權重矩陣W(可學習)V:詞典大小M:新的詞向量大小
w_i \cdot Q = c_i \\
詞矩陣C = [c_1,c_2,\cdots,c_n]\\
w_{1\times V}:詞的one-hot編碼的向量\\
Q_{V\times M}:嵌入矩陣,類似于權重矩陣W(可學習)\\
V:詞典大小\\
M:新的詞向量大小
wi??Q=ci?詞矩陣C=[c1?,c2?,?,cn?]w1×V?:詞的one?hot編碼的向量QV×M?:嵌入矩陣,類似于權重矩陣W(可學習)V:詞典大小M:新的詞向量大小
隱藏層/第一層感知機
h=Tanh(CW+b1) h = Tanh(CW+b_1) h=Tanh(CW+b1?)
輸出層/第二層感知機
O1×V=SoftMax(Uh+b2)=Softmax(U(Tanh(CW+b1))+b2) O_{1\times V} = SoftMax(Uh+b_2) = Softmax(U(Tanh(CW+b_1))+b_2) O1×V?=SoftMax(Uh+b2?)=Softmax(U(Tanh(CW+b1?))+b2?)
詞向量 && 詞嵌入-Word Embedding
能對one-hot編碼的向量起到壓縮的作用
(把一個維數為所有詞的數量的高維空間嵌入到一個維數低得多的連續向量空間中,每個單詞或詞組被映射為實數域上的向量)
w1×V?QV×M=c1×Mci就稱為詞向量
w_{1\times V}\cdot Q_{V\times M} = c_{1\times M}\\
c_i就稱為詞向量
w1×V??QV×M?=c1×M?ci?就稱為詞向量
詞向量:用一個向量表示一個單詞;所以one-hot編碼也是詞向量的一種形式
解決了任務:
- 概率評估任務:將詞轉換成詞向量了,那么就可以輸入到神經網絡中,是二分類或者多分類問題
- 生成任務:NNLM中的softmax給出的概率分布
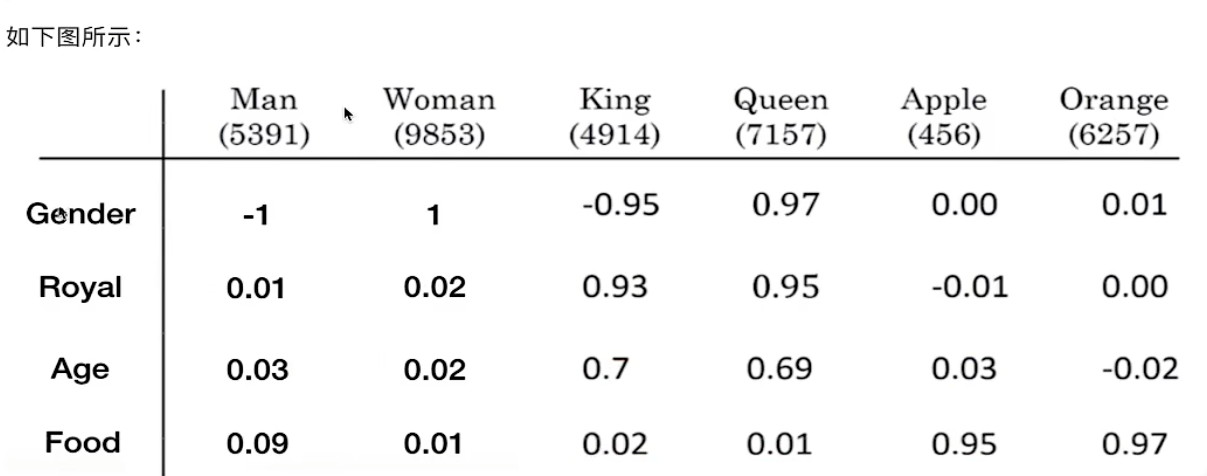
特點
- 能夠體現出詞與詞之間的關系
- 比如用Man-Woman或者Apple-Orange,都能得到一個向量
- 能夠找到相似詞
- 例如Man-Woman = King-? (?=Queen)
Word2Vec
也可以理解成一種神經網絡語言模型
與NNLM的區別
- NNLM:重點是預測下一個詞
- Word2Vec:重點是得到
Q矩陣
重要假設:文本中離得越近的詞語相似度越高

skip-gram(跳字模型)
使用中心詞預測上下文詞
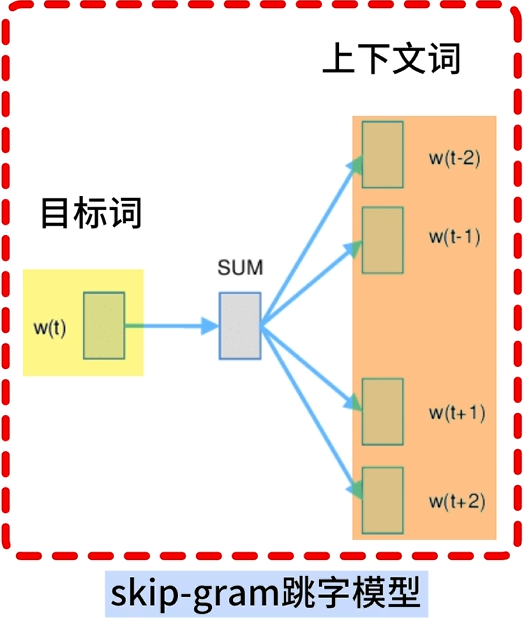
例子
假設文本序列有5個詞[“The”, “man”, “loves”, “his”, “son”],中心詞wt=“love”,背景窗口大小skip-window=2
那么上下文詞(背景詞)為"The", “man”, “his”, “son”
skip-gram做的是:通過中心詞wc,生成距離它不超過m=skip-window的背景詞,用公式表示就是:
p=P(context∣wc)=P(wc?m,wc?m+1,??,wc+m?1,wc+m∣wc)=P(wc1,wc2,??,wc2m∣wc)如果在給定中心詞的情況下,背景詞是互相獨立的,那么上面的公式可以寫成:P(context∣wt)=P(wc1∣wc)P(wc2∣wc)?P(wc2m?1∣wt)P(wc2m∣wt)wcj:第j個上下文詞wncj:第j個非上下文詞
\begin{align}
p = P(context | w_c) = P(w_{c-m},w_{c-m+1},\cdots,w_{c+m-1},w_{c+m}| w_c) = P(w_{c1},w_{c2},\cdots,w_{c2m}|w_c)\\
如果在給定中心詞的情況下,背景詞是互相獨立的,那么上面的公式可以寫成:\\
P(context |w_t) = P(w_{c1}|w_c)P(w_{c2}|w_c)\cdots P(w_{c2m-1}|w_t)P(w_{c2m}|w_t)\\
w_{cj}:第j個上下文詞\\
w_{ncj}:第j個非上下文詞
\end{align}
p=P(context∣wc?)=P(wc?m?,wc?m+1?,?,wc+m?1?,wc+m?∣wc?)=P(wc1?,wc2?,?,wc2m?∣wc?)如果在給定中心詞的情況下,背景詞是互相獨立的,那么上面的公式可以寫成:P(context∣wt?)=P(wc1?∣wc?)P(wc2?∣wc?)?P(wc2m?1?∣wt?)P(wc2m?∣wt?)wcj?:第j個上下文詞wncj?:第j個非上下文詞??
思想
使用一個詞預測另一個詞,盡量使這兩個詞的詞向量接近
skip-gram在迭代過程中,調整詞向量:
- 中心詞(目標詞)的詞向量與上下文詞(背景詞)的詞向量盡可能接近
- 中心詞詞向量與非上下文詞詞向量盡可能遠離
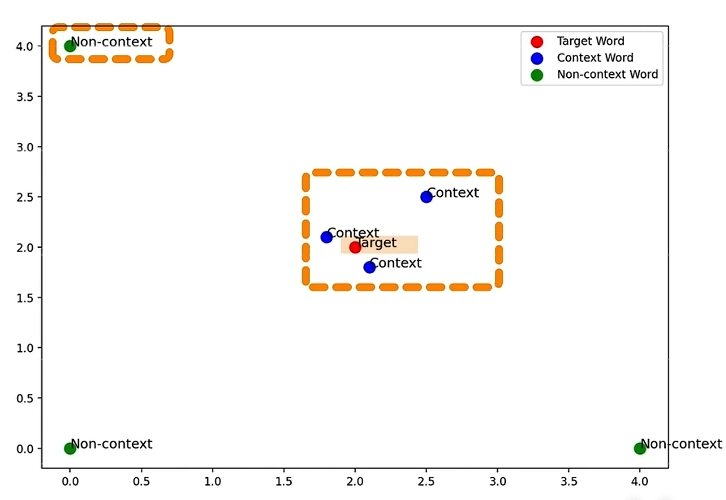
在skip-gram中,衡量兩個詞向量相似程度,采用點積的方式
點積衡量了兩個向量在同一方向上的強度,點積越大,兩個向量越相似,他們對應的詞語的語義就越接近
結構
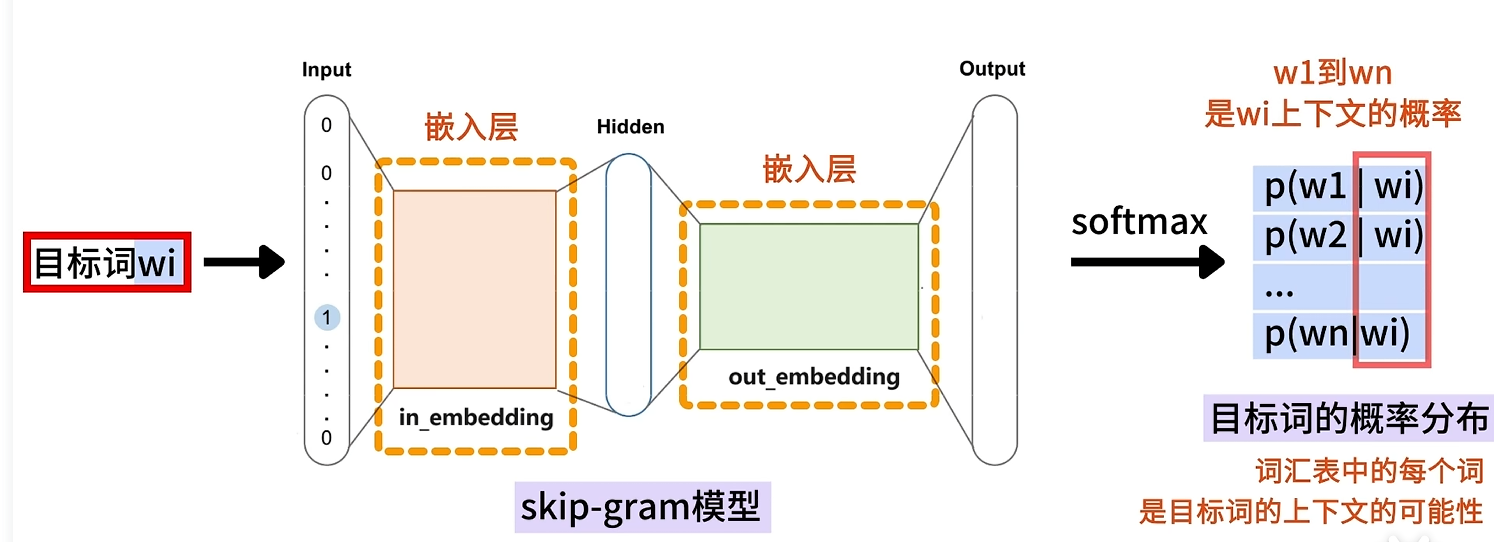
流程
和CBOW的流程其實很相似
-
one-hot編碼,將中心詞轉換成one-hot編碼形式輸入第一層嵌入層,用于計算詞向量
-
word embedding;計算中心詞的詞向量v
vi=wi?W得到形狀為1×d的中心詞詞向量viv_i = w_i\cdot W \\得到形狀為1\times d的中心詞詞向量v_ivi?=wi??W得到形狀為1×d的中心詞詞向量vi? -
skip-gram模型訓練,計算上下文詞的詞向量u
ui=vi?W′W′是d×V的矩陣,每一列對應單詞作為上下文詞的詞向量ui\begin{align}u_i = v_i\cdot W' \\W'是d\times V的矩陣,每一列對應單詞作為上下文詞的詞向量u_i\end{align}ui?=vi??W′W′是d×V的矩陣,每一列對應單詞作為上下文詞的詞向量ui??? -
softmax計算概率分布
P(wc∣wt)=exp(ucT?vt)∑i=1Vexp(uiT?vt)vt:當前中心詞詞向量uc:當前中心詞的上下文詞的詞向量\begin{align}P(w_c |w_t) = \frac{exp(u_c^T\cdot v_t)}{\sum_{i=1}^{V}exp(u_i^T\cdot v_t)} \\v_t:當前中心詞詞向量\\u_c:當前中心詞的上下文詞的詞向量\end{align}P(wc?∣wt?)=∑i=1V?exp(uiT??vt?)exp(ucT??vt?)?vt?:當前中心詞詞向量uc?:當前中心詞的上下文詞的詞向量?? -
極大化概率(求損失函數)
L=?logP(wc∣wt)=?(log(wt?m∣wt)+log(wt?m+1∣wt)+?+log(wt+m?1∣wt)+log(wt+m∣wt))\begin{align}L = -logP(w_c|w_t) = -(log(w_{t-m}|w_t)+log(w_{t-m+1}|w_t)+\cdots+log(w_{t+m-1}|w_t)+log(w_{t+m}|w_t))\end{align}L=?logP(wc?∣wt?)=?(log(wt?m?∣wt?)+log(wt?m+1?∣wt?)+?+log(wt+m?1?∣wt?)+log(wt+m?∣wt?))?? -
反向傳播更新參數矩陣
優化
在模型中出現的單詞對或短語當成一個詞
比如有些短語/單詞對的意思和一個一個單詞拼寫出的意思完全不一樣,將他們作為一個詞
二次采樣
在一個很大的語料庫中,有一些出現頻率很高的詞(比如冠詞a,the,中文的的,地,得,了之類的)
但是這些詞,提供的信息不多,會導致我們很多訓練是沒用的
因此我們引入二次采樣的思路:每個單詞都有一定概率被丟棄,這個概率為:
P(wi)=1?tf(wi)t:一個選定的閾值,通常是1e?5f(wi):單詞wi出現的頻率(次數與總單詞數的比值)
\begin{align}P(w_i) = 1-\sqrt{\frac{t}{f(w_i)}} \\t:一個選定的閾值,通常是1e-5\\f(w_i):單詞w_i出現的頻率(次數與總單詞數的比值)\\
\end{align}
P(wi?)=1?f(wi?)t??t:一個選定的閾值,通常是1e?5f(wi?):單詞wi?出現的頻率(次數與總單詞數的比值)??
為什么t取1e-5(?)
這是在 Word2Vec 原始論文和 Google 的實現中推薦的默認值
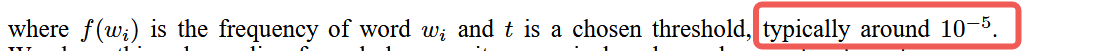
負采樣
在 Word2Vec的兩個算法中,每接收一個訓練樣本,就需要調整隱藏層和輸出層的權重參數 W,W',
來使神經網絡預測的更加準確;也就是說,每個訓練樣本都將會調整所有神經網絡中的參數
負采樣的思路是:每次讓樣本僅僅更新一小部分的權重參數,從而降低梯度下降過程中的計算量
如何去理解?
在skip-gram中,我們的目標是學習中心詞和上下文詞之間的語義關系,可以分為兩種詞:
- 正詞/正樣本(positive word):真正出現在當前詞上下文的詞(即給定的中心詞wtw_twt?及其上下文詞wcw_cwc?)
- 負詞/負樣本(negative word):隨機從詞匯表中采樣出的詞,不是當前詞的上下文詞,即與當前詞沒用上下文關系
那么為什么這樣就可以更新小部分的權重矩陣了呢(?)
原本我們需要更新所有詞對應的權重,現在我們只要更新正詞以及采樣的負詞對應的權重
這里的權重指的是輸出嵌入層參數W'
負樣本的選擇
選擇的經驗公式為:
P(wi)=f(wi)3/4∑j=1Vf(wj)3/4
P(w_i) = \frac{f(w_i)^{3/4}}{\sum_{j=1}^{V}f(w_j)^{3/4}}
P(wi?)=∑j=1V?f(wj?)3/4f(wi?)3/4?
3/4是純基于經驗的選擇
正樣本概率
給定中心詞w和上下文詞qpq^=σ(xwT?θq)xw∈R1×N:中心詞w的低維密集向量(詞嵌入后的詞向量)θq∈RN×1:輸出參數矩陣W’∈RN×V中q對應的上下文向量對于正樣本,我們希望pq^越大越好 \begin{align} 給定中心詞w和上下文詞q\\ \hat{p_q} = \sigma(x_w^T\cdot \theta^q) \\ x_w \in R^{1\times N}:中心詞w的低維密集向量(詞嵌入后的詞向量) \\ \theta^q \in R^{N\times 1}:輸出參數矩陣W’ \in R^{N\times V} 中q對應的上下文向量\\ 對于正樣本,我們希望\hat{p_q}越大越好 \end{align} 給定中心詞w和上下文詞qpq?^?=σ(xwT??θq)xw?∈R1×N:中心詞w的低維密集向量(詞嵌入后的詞向量)θq∈RN×1:輸出參數矩陣W’∈RN×V中q對應的上下文向量對于正樣本,我們希望pq?^?越大越好??
為什么不再使用Softmax而是使用sigmoid了(?)
- 引入負采樣后,問題可以被看成是一個二分類:是否是正樣本?
- 而且
Softmax分母需要計算所有詞的exp(),sigmoid不用
負樣本概率
$$
\begin{align}
選擇負樣本詞u\
\hat{p_u} = \sigma(w_w^T\cdot \theta^u) \
我們希望\hat{p_q}越小越好
\end{align}
$$
總樣本
給定(w,context(w)),可構造∣(w,context(w))∣個正樣本對于每個正樣本(w,q),q∈context(w),采樣一組負樣本NEG(q)進行對比學習則構造出∣NEG(q)∣個負樣本,負樣本為(w,u),u∈NEG(q)每個中心詞w的損失函數設計為:Lw=∏q∈context(w)(pq^∏u∈NEG(q)(1?pu^))對于語料庫C:LC=∏w∈CLw為了計算方便,進行取對數操作:Lc=∑w∈ClogLw=∑w∈C∑q∈context(w)log(pq^∏u∈NEG(q)(1?pu^))=∑w∈C∑q∈context(w)(logpq^+∑u∈NEG(q)log(1?pu^)) \begin{align} 給定(w,context(w)),可構造|(w,context(w))|個正樣本\\ 對于每個正樣本(w,q),q \in context(w),采樣一組負樣本NEG(q)進行對比學習\\ 則構造出|NEG(q)|個負樣本,負樣本為(w,u),u \in NEG(q) \\ 每個中心詞w的損失函數設計為: \\ L_w = \prod_{q \in context(w)}(\hat{p_q} \prod_{u \in NEG(q)}(1-\hat{p_u}))\\ 對于語料庫C:\\ L_C = \prod_{w \in C}L_w\\ 為了計算方便,進行取對數操作:\\ L_c = \sum_{w \in C}logL_w \\ =\sum_{w \in C}\sum_{q \in context(w)}log(\hat{p_q}\prod_{u \in NEG(q)}(1-\hat{p_u}))\\ =\sum_{w \in C}\sum_{q \in context(w)}(log\hat{p_q}+\sum_{u \in NEG(q)}log(1-\hat{p_u}))\\ \end{align} 給定(w,context(w)),可構造∣(w,context(w))∣個正樣本對于每個正樣本(w,q),q∈context(w),采樣一組負樣本NEG(q)進行對比學習則構造出∣NEG(q)∣個負樣本,負樣本為(w,u),u∈NEG(q)每個中心詞w的損失函數設計為:Lw?=q∈context(w)∏?(pq?^?u∈NEG(q)∏?(1?pu?^?))對于語料庫C:LC?=w∈C∏?Lw?為了計算方便,進行取對數操作:Lc?=w∈C∑?logLw?=w∈C∑?q∈context(w)∑?log(pq?^?u∈NEG(q)∏?(1?pu?^?))=w∈C∑?q∈context(w)∑?(logpq?^?+u∈NEG(q)∑?log(1?pu?^?))??
CBOW(連續詞袋模型)
使用上下文詞預測中心詞
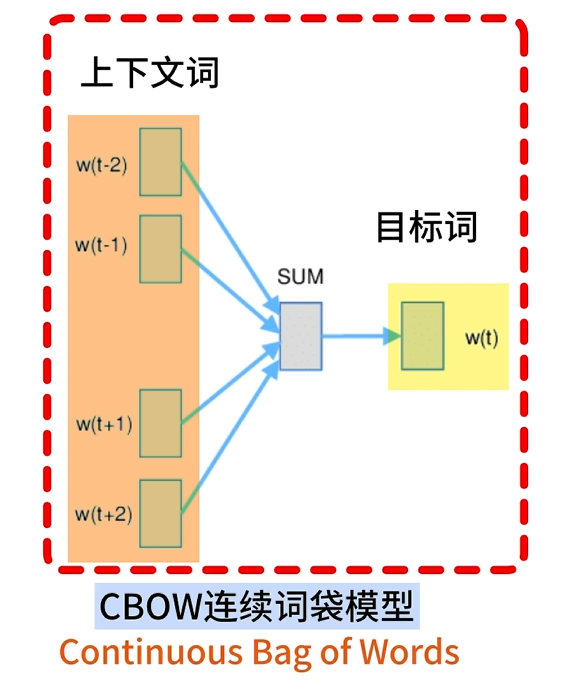
前向傳播
embeddings層
embeddings層其實是輸入層和投影層的結合,負責接受輸入的詞索引,并映射成詞向量后輸出
輸入的one?hot編碼向量為w1×Vembeddings層是一個V×M的矩陣Q,其中:V:詞典中詞語個數M:詞向量維度Q就是我們最終希望得到的嵌入矩陣
\begin{align}
輸入的one-hot編碼向量為w_{1\times V}\\
embeddings層是一個V\times M的矩陣Q,其中:\\
V:詞典中詞語個數\\
M:詞向量維度\\
Q就是我們最終希望得到的嵌入矩陣\\
\end{align}
輸入的one?hot編碼向量為w1×V?embeddings層是一個V×M的矩陣Q,其中:V:詞典中詞語個數M:詞向量維度Q就是我們最終希望得到的嵌入矩陣??
一個詞的上下文會包含多個詞語,這些詞語會被同時輸入embeddings層,每個詞語都會轉換成一個詞向量
w1Q=c1w2Q=c2?wkQ=ckC=[c1,c2,??,ck]C是序列對應的詞向量矩陣,每個元素ci(每一行)對應一個詞的word?embedding輸入embeddings層k個上下文詞,得到k個對應的詞向量需要對多個上下文詞進行統一表示:h=1k∑i=1kci
\begin{align}
w_1Q = c_1 \\
w_2Q = c_2\\
\vdots\\
w_kQ = c_k\\
C = [c_1,c_2,\cdots,c_k]\\
C是序列對應的詞向量矩陣,每個元素c_i(每一行)對應一個詞的word\ embedding\\
輸入embeddings層k個上下文詞,得到k個對應的詞向量\\
需要對多個上下文詞進行統一表示:\\
h = \frac{1}{k}\sum_{i=1}^{k}c_i
\end{align}
w1?Q=c1?w2?Q=c2??wk?Q=ck?C=[c1?,c2?,?,ck?]C是序列對應的詞向量矩陣,每個元素ci?(每一行)對應一個詞的word?embedding輸入embeddings層k個上下文詞,得到k個對應的詞向量需要對多個上下文詞進行統一表示:h=k1?i=1∑k?ci???
embeddings層的輸出結果就是:將語義信息平均的向量h
embeddings層的本質就是一個查找表(look up table),因為其每一行都對應著一個詞向量(如圖所示)
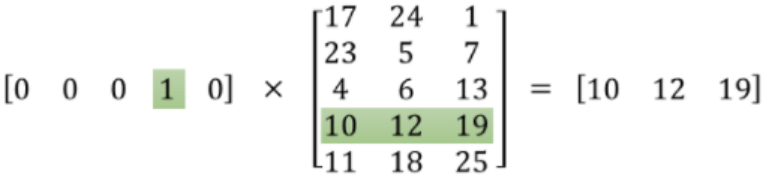
優點
- embeddings層是可訓練的,也就是說每一行對應的詞向量可以更新,使最終詞與詞之間的語義關系能更好的表示
- 可以不進行矩陣運算,僅進行查表操作,效率高很多
線性層/輸出層
特點:不設置激活函數
前面的embeddings層輸入進來的向量h∈R1×M線性層的輸出的結果是一個詞向量v∈R1×V所以線性層的權重矩陣W∈RM×Vv1×V=h?Wv=[u1,u2,??,uV]第j個詞的得分uj=WjThWj:線性層權重矩陣的第i行線性層輸出U=[u1,u2,??,um]
\begin{align}
前面的embeddings層輸入進來的向量h \in R^{1\times M} \\
線性層的輸出的結果是一個詞向量v \in R^{1\times V} \\
所以線性層的權重矩陣W \in R^{M\times V} \\
v_{1\times V} =h\cdot W\\
v = [u_1,u_2,\cdots,u_V] \\
第j個詞的得分u_j = W_j^Th\\
W_j:線性層權重矩陣的第i行\\
線性層輸出U = [u_1,u_2,\cdots,u_m]
\end{align}
前面的embeddings層輸入進來的向量h∈R1×M線性層的輸出的結果是一個詞向量v∈R1×V所以線性層的權重矩陣W∈RM×Vv1×V?=h?Wv=[u1?,u2?,?,uV?]第j個詞的得分uj?=WjT?hWj?:線性層權重矩陣的第i行線性層輸出U=[u1?,u2?,?,um?]??
為什么CBOW中不設置激活函數Tanh或者ReLU呢(?)
LLNM中設置激活函數(第一層感知機)是為了讓預測下一個詞變得更準確- 但是
CBOW中,我們只是想得到嵌入矩陣Q,然后進行正常的反向傳播更新Q和W就可以- 并且embeddings層輸出時,是進行了求平均向量這步線性操作,如果使用了非線性的激活函數,會破壞詞向量之間的語義關系
Softmax層
將線性層的輸出向量轉換為概率分布
P(yj∣context)=exp(uj)∑i=1Vexp(ui)
P(y_j | context) = \frac{exp(u_j)}{\sum_{i=1}^{V}exp(u_i)}
P(yj?∣context)=∑i=1V?exp(ui?)exp(uj?)?
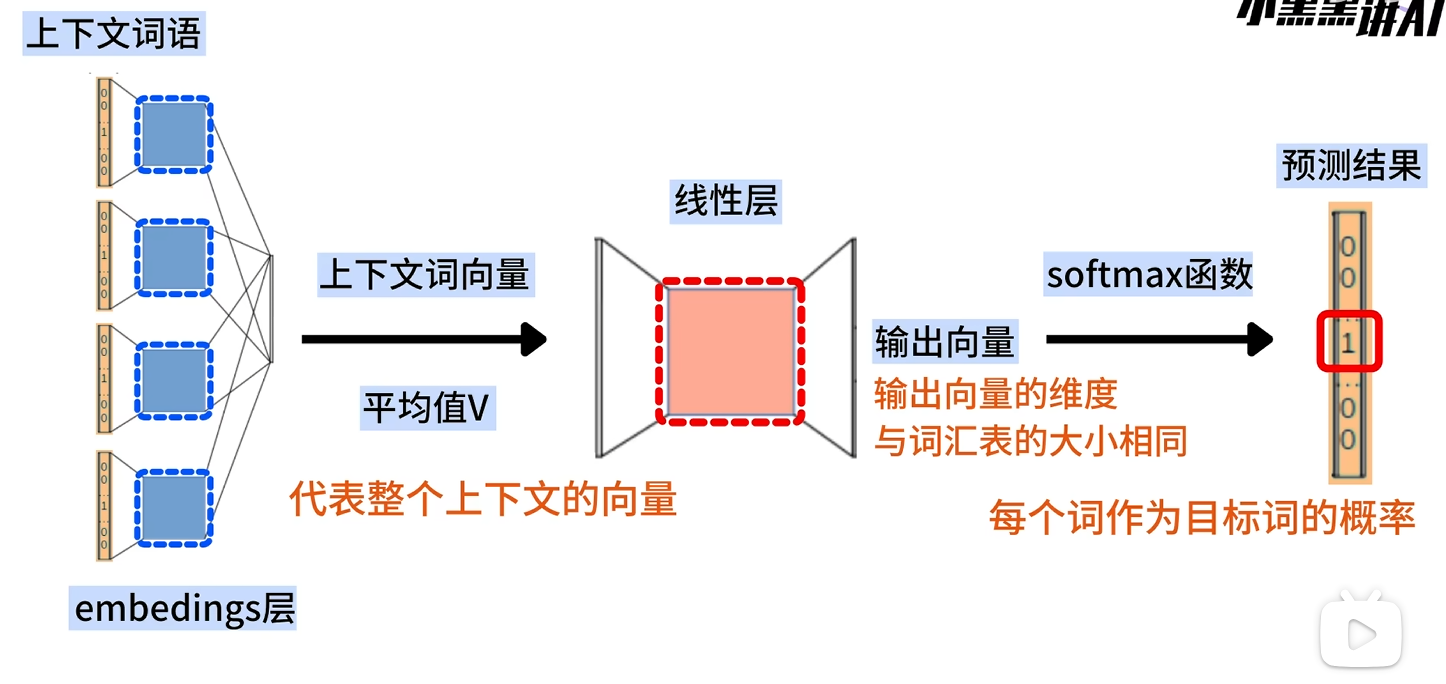
損失函數
L=?logP(wt∣wc)=?logPtruewt:中心詞wc:所有上下文詞Ptrue:Softmax輸出的對應目標詞位置的概率 \begin{align} L = -logP(w_t | w_c) = -logP_{true} \\ w_t:中心詞\\ w_c:所有上下文詞\\ P_{true}:Softmax輸出的對應目標詞位置的概率 \end{align} L=?logP(wt?∣wc?)=?logPtrue?wt?:中心詞wc?:所有上下文詞Ptrue?:Softmax輸出的對應目標詞位置的概率??
使用mini-batch進行訓練:
L=?1B∑i=1BlogP(wt(i)∣wc(i))B:Batch_size;一個Batch的樣本數(i):第i個樣本
\begin{align}
L = -\frac{1}{B}\sum_{i=1}^{B}logP(w_t^{(i)}|w_c^{(i)}) \\
B:Batch\_size;一個Batch的樣本數\\
^{(i)}:第i個樣本
\end{align}
L=?B1?i=1∑B?logP(wt(i)?∣wc(i)?)B:Batch_size;一個Batch的樣本數(i):第i個樣本??
反向傳播
先回顧一下前向傳播;embeddings層輸出:h=1V∑i=1Vwi?Q線性層:uj=WjThU=[u1,u2,??,um]Softmax層:pj=P(wj∣context)=exp(uj)∑i=1Vexp(ui) \begin{align} 先回顧一下前向傳播;\\ embeddings層輸出:h = \frac{1}{V}\sum_{i=1}^{V}w_i\cdot Q \\ 線性層:u_j = W_j^Th\\ U = [u_1,u_2,\cdots,u_m]\\ Softmax層:p_j = P(w_j|context) = \frac{exp(u_j)}{\sum_{i=1}^{V}exp(u_i)}\\ \end{align} 先回顧一下前向傳播;embeddings層輸出:h=V1?i=1∑V?wi??Q線性層:uj?=WjT?hU=[u1?,u2?,?,um?]Softmax層:pj?=P(wj?∣context)=∑i=1V?exp(ui?)exp(uj?)???
對于損失函數:
E=?logP(wt∣wc)=?log(exp(ut)∑i=1Vexp(ui))=?log(exp(WtT?h)∑i=1Vexp(WiT?h))=?(WtT?h?log∑i=1Vexp(WiT?h))=?WtT?h+log∑i=1Vexp(WiT?h)=?WtT?∑i=1Vwi?QV+log∑i=1Vexp(WiT?∑i=1Vwi?Q)V
\begin{align}
E = -logP(w_t | w_c)\\
=-log(\frac{exp(u_{t})}{\sum_{i=1}^{V}exp(u_i)})\\
= -log(\frac{exp(W^T_{t}\cdot h)}{\sum_{i=1}^{V}exp(W_i^T\cdot h)})\\
=-(W_t^T\cdot h - log\sum_{i=1}^{V}exp(W_i^T\cdot h))\\
=-W_t^T\cdot h + log\sum_{i=1}^{V}exp(W_i^T\cdot h)\\
=-\frac{W_t^T\cdot \sum_{i=1}^{V}w_i\cdot Q}{V}+log\sum_{i=1}^{V}\frac{exp(W_i^T\cdot \sum_{i=1}^{V}w_i\cdot Q)}{V}
\end{align}
E=?logP(wt?∣wc?)=?log(∑i=1V?exp(ui?)exp(ut?)?)=?log(∑i=1V?exp(WiT??h)exp(WtT??h)?)=?(WtT??h?logi=1∑V?exp(WiT??h))=?WtT??h+logi=1∑V?exp(WiT??h)=?VWtT??∑i=1V?wi??Q?+logi=1∑V?Vexp(WiT??∑i=1V?wi??Q)???
計算梯度
首先是對線性層的權重矩陣W求梯度:對當前的中心詞wt?Wt=?E?Wt=??Wt(?WtT?h+log∑i=1Vexp(WiT?h))=?h+??Wtexp(WtT?h)∑i=1Vexp(WiT?h)=?h+exp(WtT?h)?h∑i=1Vexp(WiT?h)=?h+pt?h=(pt?1)?h對其他上下文詞wc?Wc=?E?Wc=??Wc(?WtT?h+log∑i=1Vexp(WiT?h))=pc?h可以得到一個統一形式:?W=(pi?yi)?h??(yi=1,當i=t) \begin{align} 首先是對線性層的權重矩陣W求梯度:\\ 對當前的中心詞w_t\\ \nabla_{W_t} = \frac{\partial E}{\partial W_t}=\frac{\partial}{\partial W_t}(-W_t^T\cdot h + log\sum_{i=1}^{V}exp(W_i^T\cdot h))\\ = -h +\frac{\frac{\partial}{\partial W_t}exp(W_t^T\cdot h)}{\sum_{i=1}^{V}exp(W_i^T\cdot h)} = -h+\frac{exp(W_t^T\cdot h)\cdot h}{\sum_{i=1}^{V}exp(W_i^T\cdot h)} = -h+p_t\cdot h = (p_t-1)\cdot h\\ 對其他上下文詞w_c\\ \nabla_{W_c} = \frac{\partial E}{\partial W_c}=\frac{\partial}{\partial W_c}(-W_t^T\cdot h + log\sum_{i=1}^{V}exp(W_i^T\cdot h))\\ =p_c\cdot h\\ 可以得到一個統一形式:\\ \nabla_{W} = (p_i-y_i)\cdot h\ \ (y_i=1,當i=t) \end{align} 首先是對線性層的權重矩陣W求梯度:對當前的中心詞wt??Wt??=?Wt??E?=?Wt???(?WtT??h+logi=1∑V?exp(WiT??h))=?h+∑i=1V?exp(WiT??h)?Wt???exp(WtT??h)?=?h+∑i=1V?exp(WiT??h)exp(WtT??h)?h?=?h+pt??h=(pt??1)?h對其他上下文詞wc??Wc??=?Wc??E?=?Wc???(?WtT??h+logi=1∑V?exp(WiT??h))=pc??h可以得到一個統一形式:?W?=(pi??yi?)?h??(yi?=1,當i=t)??
對embeddings層的嵌入矩陣Q求梯度:?Q=?E?U?U?h?h?Q=(pi?yi)?Wi???Q(1V∑i=1Vwi?Q)=1V((pi?yi)?Wi?∑i=1Vwi)因為wi是one?hot編碼得到的二進制向量∑i=1Vwi相當于是一個長度為V的全1向量所以得到最終的梯度:?Q=1V(pi?yi)?Wi \begin{align} 對embeddings層的嵌入矩陣Q求梯度:\\ \nabla_Q = \frac{\partial E}{\partial U}\frac{\partial U}{\partial h}\frac{\partial h}{\partial Q}\\ =(p_i-y_i)\cdot W_i\cdot \frac{\partial}{\partial Q}(\frac{1}{V}\sum_{i=1}^{V}w_i\cdot Q )\\ =\frac{1}{V}((p_i-y_i)\cdot W_i\cdot \sum_{i=1}^{V}w_i) \\ 因為w_i是one-hot編碼得到的二進制向量 \\ \sum_{i=1}^{V}w_i相當于是一個長度為V的全1向量\\ 所以得到最終的梯度:\\ \nabla_Q = \frac{1}{V}(p_i-y_i)\cdot W_i \end{align} 對embeddings層的嵌入矩陣Q求梯度:?Q?=?U?E??h?U??Q?h?=(pi??yi?)?Wi???Q??(V1?i=1∑V?wi??Q)=V1?((pi??yi?)?Wi??i=1∑V?wi?)因為wi?是one?hot編碼得到的二進制向量i=1∑V?wi?相當于是一個長度為V的全1向量所以得到最終的梯度:?Q?=V1?(pi??yi?)?Wi???
層次Softmax(Hierarchical Softmax)
前置知識
哈夫曼樹
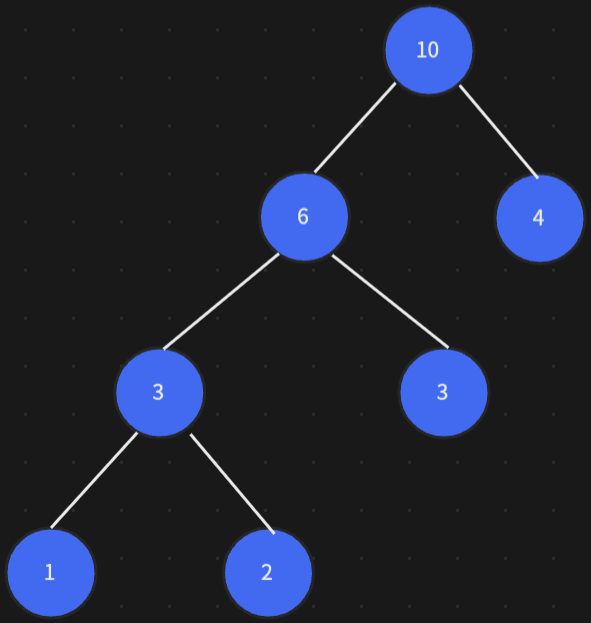
哈夫曼樹是保證所有葉子節點的帶權路徑長度最小的一種樹
比如對于這樣一顆二叉樹
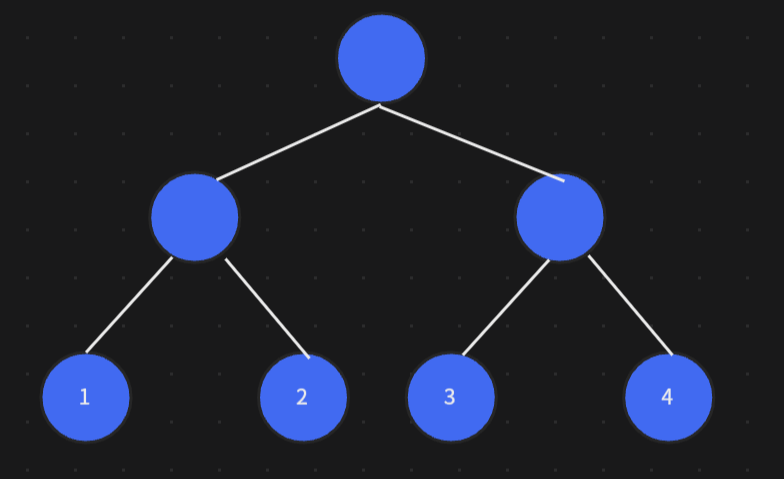
首先找出兩個最小的葉子節點,組成一顆新的樹
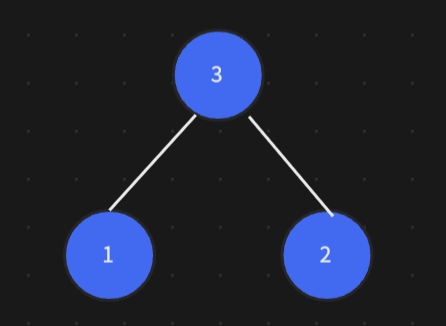
找出下一個最小的葉子節點,與新樹組成樹
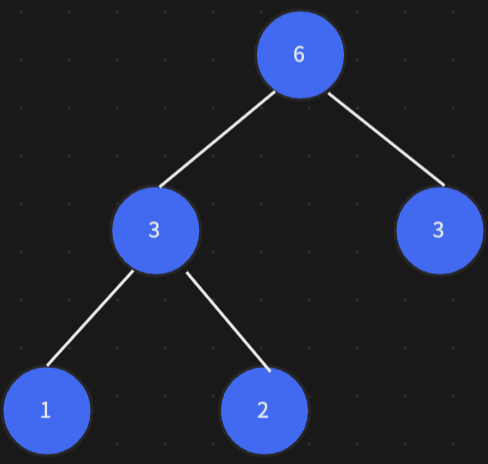
以此類推,最終組成哈夫曼樹
優化點
-
類似于
CBOW的embeddings層,從輸入層到隱藏層的映射,不是像神經網絡那樣線性變換+激活函數的操作,而是對詞向量求平均 -
原本我們計算Softmax:
P(wc∣wt)=exp(ucT?vt)∑i=1Vexp(uiT?vt)vt:當前中心詞詞向量uc:當前中心詞的上下文詞的詞向量\begin{align}P(w_c |w_t) = \frac{exp(u_c^T\cdot v_t)}{\sum_{i=1}^{V}exp(u_i^T\cdot v_t)} \\v_t:當前中心詞詞向量\\u_c:當前中心詞的上下文詞的詞向量\end{align}P(wc?∣wt?)=∑i=1V?exp(uiT??vt?)exp(ucT??vt?)?vt?:當前中心詞詞向量uc?:當前中心詞的上下文詞的詞向量??
需要遍歷整個詞匯表,對于大詞匯表來說,這個做法的效率太災難了
因此,層次Softmax通過將詞匯表構造成樹形結構,從而減少了計算量,特別是在計算時只需要經過樹的部分路徑,而不是整個詞匯表
工作原理
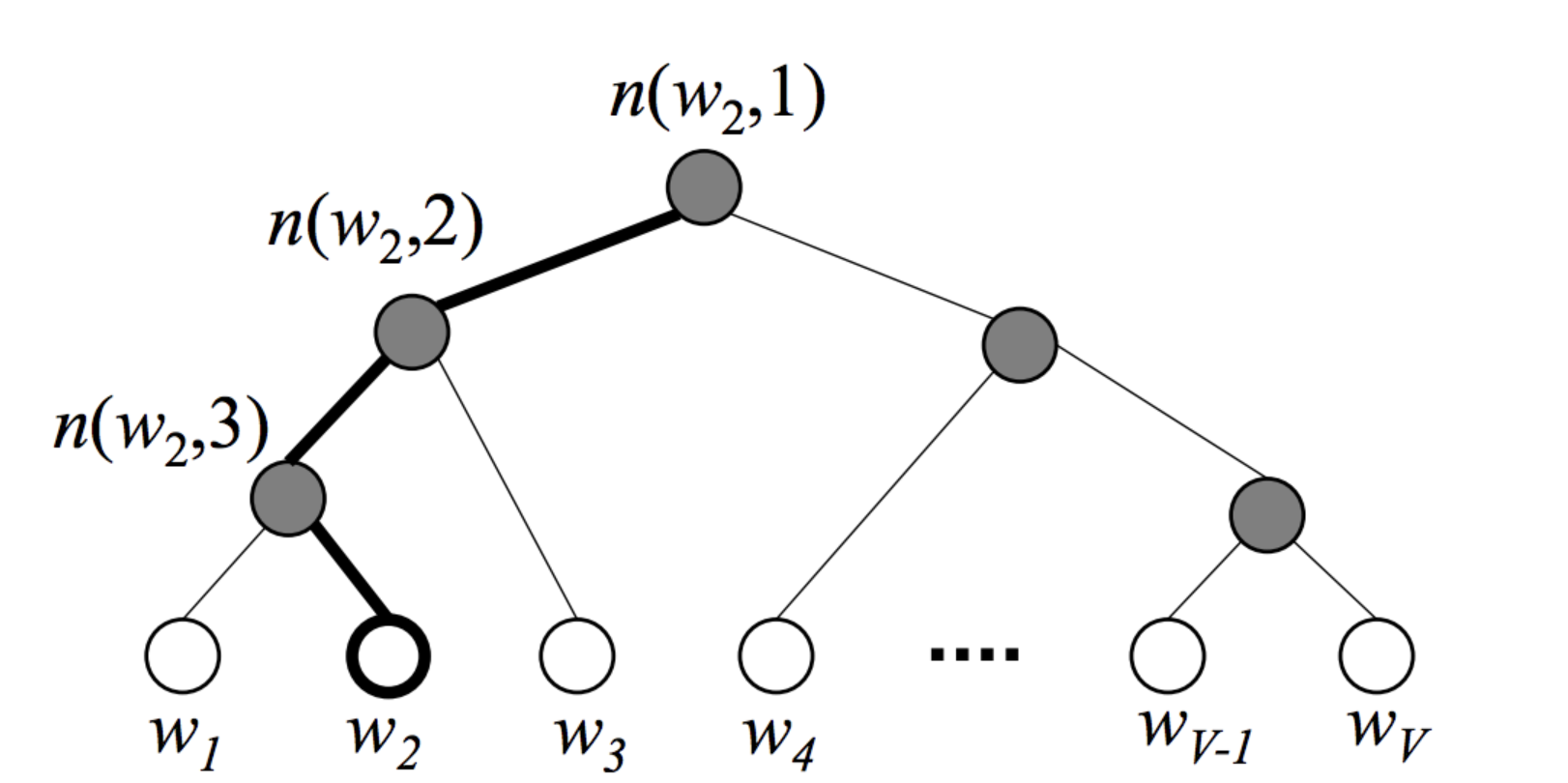
將詞匯表V中的所有詞匯根據詞頻f(wi))f(w_i))f(wi?))表示成一顆哈夫曼樹,詞頻越大,路徑越短,編碼信息更少;其中葉子節點表示對應的詞wiw_iwi?,非葉子節點表示決策路徑(二分類決策),每個葉子節點都有唯一的從根節點到該節點的路徑path
比如對于葉子節點w2w_2w2?,從根節點出發到w2w_2w2?的路徑為:
n(w2,1),n(w2,2),n(w2,3),w2n(wi,j):詞wi的path的第j個節點
\begin{align}
n(w_2,1),n(w_2,2),n(w_2,3),w_2\\
n(w_i,j):詞w_i的path的第j個節點
\end{align}
n(w2?,1),n(w2?,2),n(w2?,3),w2?n(wi?,j):詞wi?的path的第j個節點??
葉子節點詞的概率表示
在Hierarchical Softmax中,我們的目標是計算根節點到葉子節點的路徑的概率,并最大化路徑上每個節點的概率;根節點到葉子節點有很多中間節點nkn_knk?,每個中間節點的決策都是二分類問題
那么就有正類(+)與負類(-)的區分:在這里規定向左為負(-)
使用sigmoid判斷正負類:
P(+)=σ(vnT′?h)vnT′:中間節點詞向量h:隱藏層輸出的中心詞的上下文向量 \begin{align} P(+) = \sigma(v_n^T{'} \cdot h) \\ v_n^T{'}:中間節點詞向量\\ h:隱藏層輸出的中心詞的上下文向量 \end{align} P(+)=σ(vnT?′?h)vnT?′:中間節點詞向量h:隱藏層輸出的中心詞的上下文向量??
還是計算上面根節點到w2w_2w2?路徑的概率,我們應最大化下式:
P(w2)=∏i=13P(n(w2,i))=P(n(w2,1),?)?P(n(w2,2),?)?P(n(w2,3),+)=σ(?vn(w2,1)T′?h)?σ(?vn(w2,2)T′?h)?σ(vn(w2,3)T′?h) \begin{align} P(w_2) = \prod_{i=1}^{3}P(n(w_2,i)) = P(n(w_2,1),-)\cdot P(n(w_2,2),-)\cdot P(n(w_2,3),+) \\ =\sigma(-v_{n(w_2,1)}^T{'} \cdot h)\cdot\sigma(-v_{n(w_2,2)}^T{'} \cdot h)\cdot\sigma(v_{n(w_2,3)}^T{'} \cdot h) \end{align} P(w2?)=i=1∏3?P(n(w2?,i))=P(n(w2?,1),?)?P(n(w2?,2),?)?P(n(w2?,3),+)=σ(?vn(w2?,1)T?′?h)?σ(?vn(w2?,2)T?′?h)?σ(vn(w2?,3)T?′?h)??
損失函數:
E=?logP(w2)=?∑i=13logP(n(w2,i))=?∑i=13logσ(signi?vn(w2,i)T′?h)signi:表示向左(?1)向右(+1)
\begin{align}
E = -logP(w_2) = -\sum_{i=1}^{3}logP(n(w_2,i)) = -\sum_{i=1}^{3}log\sigma(sign_i \cdot v_{n(w_2,i)}^T{'} \cdot h)\\
sign_i:表示向左(-1)向右(+1)
\end{align}
E=?logP(w2?)=?i=1∑3?logP(n(w2?,i))=?i=1∑3?logσ(signi??vn(w2?,i)T?′?h)signi?:表示向左(?1)向右(+1)??
通過梯度下降更新vnT′和hv_n^T{'} 和 hvnT?′和h
案例
設備
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(f"current device:{device}")
數據
# 句子數據
sentences = [ # 動物行為 "dogs chase cats", "cats drink milk", "dogs love bones", "cats hate water", "dogs bark loudly", "cats climb trees", "dogs play fetch", "cats purr softly", "dogs guard houses", "cats hunt mice", "dogs wag tails", "cats nap all day", "birds fly high", "fish swim fast", "birds sing in morning", "tigers roar at night", "elephants walk slowly", "monkeys swing on trees", # 食物特征 "apples are sweet", "bananas taste creamy", "apples grow on trees", "bananas have peels", "apples make juice", "bananas are yellow", "apples can be red", "bananas rich in potassium", "oranges are juicy", "grapes are sour", "strawberries are red", "bread is soft", "cheese tastes salty", "eggs are nutritious", "rice is sticky", "noodles are long", "chocolate is sweet", # 日常生活 "kids eat apples", "monkeys love bananas", "dogs enjoy meat", "cats prefer fish", "people drink milk", "children like fruit", "breakfast has milk", "dogs drink water", "cats avoid dogs", "people walk to work", "buses run on time", "cars drive fast", "students study hard", "teachers explain clearly", "doctors help patients", "cooks prepare meals", "babies cry at night", "seniors rest peacefully", # 情感與動作 "he feels happy", "she looks tired", "they laugh together", "he cries softly", "she dances gracefully", "they argue loudly", "he hugs his dog", "she kisses her baby", "they shake hands", "he smiles kindly", "she yells in anger", "they cheer with joy", # 自然與天氣 "sun rises early", "moon shines at night", "stars twinkle above", "clouds float in sky", "rain falls gently", "wind blows strongly", "snow covers mountains", "ice melts in sun", "lightning flashes bright", "thunder rumbles loudly", "fog covers the fields", "dew drops sparkle", # 人物與職業 "doctors heal patients", "teachers teach students", "engineers build bridges", "writers write stories", "artists draw pictures", "singers sing songs", "actors perform plays", "pilots fly planes", "farmers grow crops", "chefs cook meals", "drivers drive cars", "scientists make discoveries", # 更多組合 "apple pie is delicious", "banana smoothie is healthy", "dog food contains nutrients", "cat food has tuna flavor", "apple and banana salad", "dog and cat live together", "milk with banana shake", "fish for cat dinner", "bread with cheese", "rice with chicken", "noodles with beef", "coffee with milk", "tea with sugar", "juice with ice"
]
構造詞匯表V以及索引與詞之間映射關系的字典
# 分詞
word_list = "".join(sentences).split() # 轉換成set去重
vocab = set(list(word_list))
# print(vocal) # 構建索引
v_to_idx = {c: i for i, c in enumerate(vocab)}
idx_to_v = {i: c for i, c in enumerate(vocab)} # 構建詞頻
f_word = Counter(vocab)
# print(f"f(w)={f_word}")# 所有詞的頻度和其實就是對原始句子數據分詞后得到的長度
f_total = len(word_list)
# print(f"\sumf(w)={f_total}")
構造負采樣的概率
# 計算負采樣概率
prob_neg_samples = {w: (cnt / f_total) ** 0.75 for w, cnt in f_word.items()}
# print(f"prob_neg_samples = {prob_neg_samples}") # 轉換成np.array的形式,其中放的是負采樣概率
prob_neg_samples = np.array([prob_neg_samples[w] for w in vocab])
# print(f"prob_neg_samples = {prob_neg_samples}")
存在問題?
當前負采樣概率和不為1,后續選擇負樣本時會出錯
解決:進行歸一化
# 歸一化
prob_neg_samples /= prob_neg_samples.sum()
修正后的構造負采樣的代碼為:
# 計算負采樣概率
prob_neg_samples = {w: (cnt / f_total) ** 0.75 for w, cnt in f_word.items()}
# print(f"prob_neg_samples = {prob_neg_samples}")# 轉換成np.array的形式,其中放的是負采樣概率
prob_neg_samples = np.array([prob_neg_samples[w] for w in vocab])
# print(f"prob_neg_samples = {prob_neg_samples}")# 歸一化
prob_neg_samples /= prob_neg_samples.sum()
生成帶負采樣的訓練數據
# 窗口大小
window_size = 2
# 1個正例對4個反例
neg_count = 4 # 生成負采樣訓練樣本
def generate_neg_sample(): skip_gram = [] # 存放((正/反例),flag) flag=True為正例 for idx in range(window_size, len(word_list) - window_size): centre = v_to_idx[word_list[idx]] # 中心詞 # 上下文詞 contexts = [v_to_idx[word_list[i]] for i in range(idx - window_size, idx + window_size + 1) if i != idx] for c in contexts: # 對中心詞-上下文詞,作為正樣本加入 skip_gram.append((centre, c, True)) # 負樣本對應詞索引集合 negs = [] # 隨機選擇負樣本 while len(negs) < neg_count: neg_idx = np.random.choice(len(vocab), p=prob_neg_samples) if neg_idx != c: negs.append(neg_idx) # 負樣本加入 for ni in negs: skip_gram.append((centre, ni, False)) return skip_gram
轉換為tensor
# 將負采樣訓練樣本轉換為torch.tensor
data = generate_neg_sample()centres = torch.tensor([d[0] for d in data], dtype=torch.long).to(device)
# print(f"centres={centres}")
contexts = torch.tensor([d[1] for d in data], dtype=torch.long).to(device)
# print(f"contexts ={contexts}")
labels = torch.tensor([d[2] for d in data], dtype=torch.float32).to(device)
# print(f"labels={labels}")
構建數據集以及分批加載
# 使用TensorDataset將三個張量合成一個數據集對象,每個樣本是一個三元組(centres, contexts, labels)
dataset = Data.TensorDataset(centres, contexts, labels)
# 按批次加載對象
dataloader = Data.DataLoader(dataset, batch_size, shuffle=True)
模型
class NegSkipGram(nn.Module): def __init__(self, vocab_size, embedding_dim): """ :param vocab_size: 詞匯表長度 :param embedding_dim: 嵌入矩陣維度 """ super().__init__() # 得到中心詞詞嵌入向量 self.centre_embedding = nn.Embedding(vocab_size, embedding_dim) # 得到上下文詞詞嵌入向量 self.context_embedding = nn.Embedding(vocab_size, embedding_dim) # 初始化兩個embedding層中的權重矩陣,使用正態分布進行原地填充(直接修改原tensor的值) nn.init.normal_( self.centre_embedding.weight, # 輸出中心詞word embedding的權重矩陣 mean=0, # 均值為0 std=0.01 # 標準差 ) nn.init.normal_( self.context_embedding.weight, # 輸出上下文詞word embedding的權重矩陣 mean=0, std=0.01 ) def forward(self, centres, contexts): """ :param centres: 中心詞詞向量 shape=[batch_size] :param contexts: 上下文詞詞向量 shape=[batch_size] :return: 余弦相似度 """ # 中心詞詞向量shape=[batch_size,embedding_dim] vec_centre = self.centre_embedding(centres) # print(f"vec_centre.shape={vec_centre.shape}") # 上下文詞詞向量shape=[batch_size,embedding_dim] vec_context = self.context_embedding(contexts) # print(f"vec_context.shape={vec_context.shape}") # print(f"vec_context={vec_context}") # 余弦相似度 return torch.cosine_similarity(vec_centre, vec_context, dim=1)模型訓練
# 一批訓練多少個樣本
batch_size = 128
# word-embedding維度
embedding_dim = 20# 模型
model = NegSkipGram(vocab_size, embedding_size).to(device)
# 二分類交叉熵損失
criterion = nn.BCEWithLogitsLoss()
# adam優化
optimiser = torch.optim.Adam(model.parameters(), lr=0.005) epochs = 100 for i in range(epochs): # 在dataloader中取出每一批的中心詞向量,上下文詞向量,標簽 for batch_centre, batch_context, batch_label in dataloader: # 獲得前向傳播分數 cos_score = model(batch_centre, batch_context) # 獲取損失函數值 loss = criterion(cos_score, batch_label) # 清空優化器中所有參數的梯度緩存 optimiser.zero_grad() loss.backward() # 更新參數 optimiser.step()可視化:使用sklearn.manifold.TSNE進行降維,以及plt進行繪圖
# 中心詞嵌入層參數矩陣的numpy形式 shape=(vocab_size,embedding_dim)
word_vectors = (# 中心詞嵌入層的權重W shape=Tensor[vocab_size,embedding_dim] model.centre_embedding.weight .cpu() # 獲取的權重矩陣轉存到cpu中 .detach() # 切斷歷史梯度 .numpy()
) # TSNE降維
tsne = TSNE( n_components=2, # 詞向量維度降到2D random_state=42, perplexity=min(5, len(vocab) - 1) # perplexity可以理解為每個點鄰居數量的估計值
) # 降維
word_vectors_2d = tsne.fit_transform(word_vectors) plt.figure(figsize=(12, 10))
for i in range(vocab_size): plt.scatter(word_vectors_2d[i, 0], word_vectors_2d[i, 1]) plt.annotate( idx_to_v[i], xy=(word_vectors_2d[i, 0], word_vectors_2d[i, 1]), xytext=(5, 2), # 標簽文字對點的偏移量 textcoords='offset points', # 指定xytext單位是點 ha='right', va='bottom' ) plt.show()問題
為什么嵌入層返回的形狀跟之前公式里學習的都不太一樣(?)
因為在torch中,我們使用了批量處理的方法,一次處理一個batch而不是一個詞;
在嵌入矩陣中,每輸入一個詞,就會輸出一個形狀為[,embedding_dim]的向量,那么對于batch_size個詞,就會輸出形狀為[batch_size,embedding_dim]的矩陣
為什么計算余弦相似度時要指定維度(?)
因為torch返回的詞向量的shape是[batch_size,embedding_dim],對embedding_dim這一維度求余弦相似度,才能正確計算這一個batch中每個詞的余弦相似度評分





——pandas庫)
![第十六屆藍橋杯青少組C++省賽[2025.8.9]第二部分編程題(1 、慶典隊列)](http://pic.xiahunao.cn/第十六屆藍橋杯青少組C++省賽[2025.8.9]第二部分編程題(1 、慶典隊列))

)









)
