【AI論文】序列標注任務廣義化研究（SFT廣義化）：基于獎勵修正的強化學習視角

摘要：我們針對大語言模型（Large Language Model，LLM）的監督微調（Supervised Fine-Tuning，SFT）提出了一種簡單但具有理論依據的改進方法，以解決其與強化學習（Reinforcement Learning，RL）相比泛化能力有限的問題。通過數學分析，我們發現標準的SFT梯度隱式地編碼了一種有問題的獎勵結構，這種結構可能會嚴重限制模型的泛化能力。為了解決這一問題，我們提出了動態微調（Dynamic Fine-Tuning，DFT）方法，該方法通過根據每個詞元的出現概率對目標函數進行動態縮放，來穩定每個詞元的梯度更新。值得注意的是，僅對代碼進行這一處簡單修改，就在多個具有挑戰性的基準測試和基礎模型上顯著優于標準SFT，展現出大幅提高的泛化能力。此外，我們的方法在離線強化學習場景中也表現出具有競爭力的結果，提供了一種有效且更簡單的替代方案。本研究將理論見解與實際解決方案相結合，顯著提升了SFT的性能。代碼將在https://github.com/yongliang-wu/DFT上公開。Huggingface鏈接：Paper page，論文鏈接：2508.05629

一、研究背景和目的

研究背景

在自然語言處理領域，大語言模型（LLM）的發展日新月異，監督微調（Supervised Fine-Tuning，SFT）作為一種常用的后訓練方法，被廣泛應用于模型對新任務的適應和現有能力的增強。SFT通過在專家演示數據集上訓練模型，使其能夠快速模仿專家行為，具有實現簡單、獲取專家模式速度快的優點。然而，與強化學習（RL）方法相比，SFT的泛化能力存在明顯局限。RL方法利用顯式的獎勵或驗證信號，允許模型探索多樣化的策略，從而實現更強的泛化能力。但在實際應用中，RL方法往往需要大量的計算資源，對超參數敏感，并且依賴于獎勵信號的可用性，這些條件并不總是能夠滿足。

盡管已有多種混合方法被開發出來，結合了SFT和RL的優勢，但在沒有負樣本、獎勵模型或驗證信號的數據集中，SFT仍然是唯一可行的選擇。因此，如何從根本上改進SFT本身，提高其泛化能力，成為了一個亟待解決的問題。

研究目的

本研究旨在通過理論分析和數學推導，揭示SFT梯度隱式編碼的問題獎勵結構，進而提出一種簡單而有效的改進方法——動態微調（DFT）。DFT的目標是通過動態調整每個詞元的損失函數，穩定梯度更新，從而提高SFT的泛化能力。本研究期望通過這一改進，使SFT在保持其原有優勢的同時，能夠更接近或達到RL方法的泛化性能，為LLM的后訓練提供一種更高效、更穩定的解決方案。

二、研究方法

理論分析與數學推導

本研究首先通過理論分析，揭示了SFT梯度與RL政策梯度之間的數學聯系。研究指出，標準的SFT梯度可以看作是一種特殊形式的政策梯度，其隱式定義的獎勵結構存在問題，具體表現為獎勵極其稀疏且與模型分配給專家動作的概率成反比。這種獎勵結構導致當模型為專家動作分配低概率時，梯度會出現無界方差，從而產生不穩定的優化景觀。

基于上述分析，研究提出了DFT方法，其核心思想是通過動態調整每個詞元的損失函數，消除隱式獎勵結構中的逆概率加權問題。具體來說，DFT通過將標準SFT目標函數與詞元概率相乘（脫鉤以避免梯度流動），實現了對每個詞元損失的動態縮放。

實驗設計與實施

為了驗證DFT方法的有效性，研究在多個具有挑戰性的數學推理基準測試和不同規模的基礎模型上進行了廣泛的實驗。實驗設置包括：

數據集：使用NuminaMath CoT數據集，包含約860,000個數學問題及其解決方案。為了高效管理計算資源，研究隨機抽取了100,000個實例進行訓練。
模型：實驗涉及多個最先進的模型，包括Qwen2.5-Math-1.5B、Qwen2.5-Math-7B、LLaMA-3.2-3B、LLaMA-3.1-8B和DeepSeekMath-7B-Base。
訓練細節：基于verl框架實現，使用推薦的SFT超參數。具體來說，采用AdamW優化器，學習率設置為5×10-5（LLaMA-3.1-8B模型為2×10-5），迷你批次大小為256，最大輸入長度為2048個詞元。學習率遵循余弦衰減計劃，預熱比率為0.1。
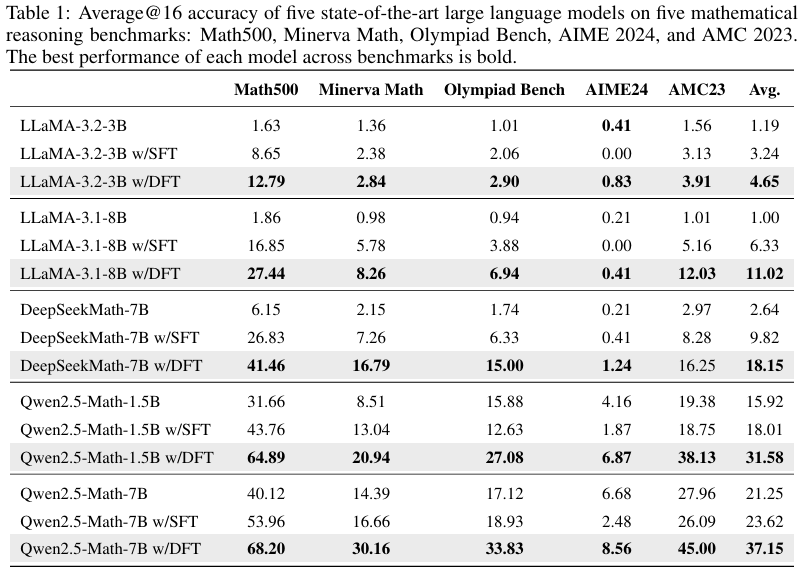
評估設置：在數學推理任務上，研究在Math500、Minerva Math、Olympiad Bench、AIME2024和AMC2023等基準測試上進行了評估。每個模型使用默認的聊天模板和思維鏈（CoT）提示來激發逐步推理。所有報告的結果均為在溫度為1.0和最大生成長度為4096個詞元下，進行16次解碼運行的平均準確率。

對比方法

為了全面評估DFT方法的性能，研究還實現了以下對比方法：

標準SFT：作為基線方法，用于比較DFT的改進效果。
重要性加權SFT（iw-SFT）：作為一種同時利用SFT和RL優勢的混合方法，用于與DFT進行對比。
離線RL方法：包括DPO和RFT/RAFT，用于在離線RL設置下評估DFT的性能。
在線RL方法：包括PPO和GRPO，用于在在線RL設置下與DFT進行比較。

三、研究結果

主要發現

DFT顯著優于標準SFT：在所有評估的LLM上，DFT的平均性能提升均顯著超過標準SFT。例如，在Qwen2.5-Math-1.5B模型上，DFT的平均準確率提升了+15.66點，是SFT提升（+2.09點）的5.9倍以上。
DFT在具有挑戰性的基準測試上表現尤為突出：在Olympiad Bench、AIME2024和AMC2023等具有挑戰性的基準測試上，標準SFT往往出現性能下降，而DFT則能夠持續提供顯著的性能提升。例如，在Olympiad Bench上，SFT使Qwen2.5-Math-1.5B的準確率從15.88降至12.63，而DFT則將其提升至27.08。
DFT在離線RL設置下表現優異：在利用拒絕采樣生成的獎勵信號的離線RL設置下，DFT的表現超過了所有離線RL基線方法，甚至超過了最強的在線RL算法GRPO。例如，在Qwen2.5-Math-1.5B模型上，DFT的平均得分達到了35.43，超過了GRPO的32.00。
DFT的收斂速度更快：與標準SFT相比，DFT在大多數基準測試上表現出更快的收斂速度。通常在120個訓練步驟內就能達到峰值性能，而SFT則需要更多的訓練步驟。

深入分析

詞元概率分布變化：研究通過分析模型在訓練集上的詞元概率分布變化，發現DFT與標準SFT在優化過程中對詞元概率的調整方式存在顯著差異。標準SFT傾向于均勻增加所有詞元的概率，而DFT則顯著提升了部分詞元的概率，同時主動抑制了其他詞元的概率，導致詞元概率分布呈現雙峰分布。
超參數敏感性分析：研究通過消融實驗評估了DFT對關鍵訓練超參數的敏感性，發現DFT在不同學習率和批次大小下均能保持穩定的性能提升，表明DFT對超參數的選擇具有較強的魯棒性。

四、研究局限

盡管本研究在提高SFT泛化能力方面取得了顯著成果，但仍存在以下局限：

評估范圍有限：目前的研究僅在數學推理基準測試和最多70億參數的模型上進行了評估，未在其他任務領域（如代碼生成、常識問答）和更大規模的LLM（如130億+參數）上進行驗證。
文本場景限制：當前研究僅限于文本場景，未在視覺語言任務上驗證DFT的有效性。
理論分析的簡化假設：在理論分析中，研究對SFT梯度與RL政策梯度之間的聯系進行了一定的簡化假設，這些假設在實際應用中可能不完全成立。

五、未來研究方向

針對上述研究局限，未來的研究可以從以下幾個方面展開：

擴展評估范圍：將DFT方法應用于更廣泛的任務領域和更大規模的LLM上，以驗證其普適性和有效性。特別是在代碼生成、常識問答等非數學推理任務上，評估DFT的泛化能力。
多模態場景驗證：在視覺語言任務上驗證DFT的有效性，探索其在多模態大語言模型后訓練中的應用潛力。
深化理論分析：進一步放松理論分析中的簡化假設，更精確地揭示SFT梯度與RL政策梯度之間的聯系，為DFT方法的優化提供更堅實的理論基礎。
結合其他先進技術：探索將DFT與其他先進技術（如元學習、遷移學習）相結合的可能性，以進一步提高LLM的后訓練性能和泛化能力。
實際應用探索：將DFT方法應用于實際場景中，如智能客服、內容生成等，評估其在真實世界中的表現和價值。