【C++】STL二叉搜索樹——map與set容器的基礎結構

目錄

前言

1.二叉搜索樹的概念

1.1基本結構

1.2性能分析

2.二叉搜索樹的實現

2.1創建

2.2插入

2.3查找與遍歷

2.4刪除

3.二叉搜索樹類代碼

前言

C++中STL的map與set容器廣泛應用于實踐過程中，本文將詳細分析容器最基礎的二叉搜索樹結構，為后續map與set容器的學習打下更好基礎。更多C++內容可前往->|C++主題專欄|<-

1.二叉搜索樹的概念

1.1基本結構

二叉搜索樹是一種便于快速查找(搜索)數據的搜索結構，也稱二叉排序樹。它或是棵空樹，又或是滿足以下性質的樹：

二叉搜索樹的性質

? 若它的左?樹不為空，則左?樹上所有結點的值都?于等于根結點的值
? 若它的右?樹不為空，則右?樹上所有結點的值都?于等于根結點的值
? 它的左右?樹也分別為?叉搜索樹
? ?叉搜索樹中可以?持插?相等的值，也可以不?持插?相等的值，具體看使?場景定義

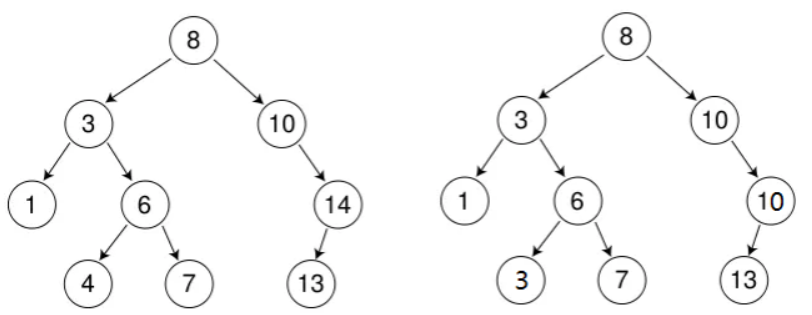
如上兩棵樹都是二叉搜索樹，當然第二棵樹的重復元素(10)可以在父節點的左子樹也可以在父節點的右子樹。但我們常用的一般是左邊無重復元素的二叉搜索樹。

1.2性能分析

以上面第一棵樹為例：這種情況下的樹基本為完全二叉樹，其搜索性能(時間復雜度)與樹的高度相同為logN。但這是最優的情況，若二叉搜索樹的數據插入滿足一定條件，就會形成類似單支樹的情況(如下圖)，這種情況下的搜索性能就會降為O(N)。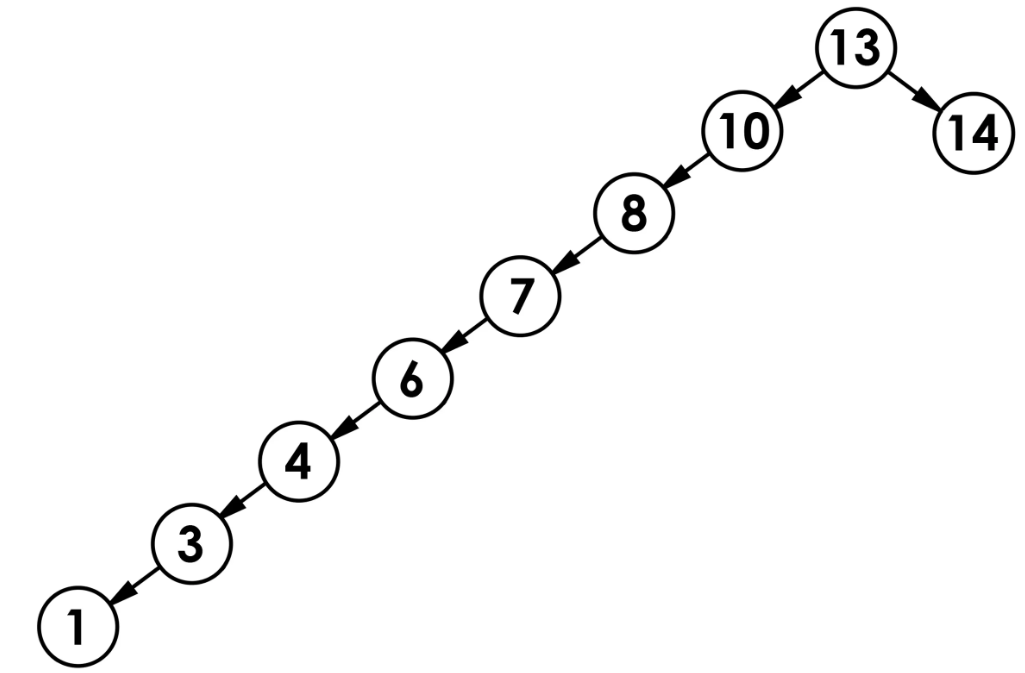

因此綜合考慮，普通搜索二叉樹的搜索性能就是O(N)，但這樣的效率顯然不夠理想，后面在實際應用時使用的是優化過平衡二叉樹(AVL樹、紅黑樹)。

其次對于查找功能，在數組中的二分查找算法也能實現O(logN)級別的查找效率，但二分查找算法對比于二叉搜索樹有著明顯的缺點：

二分查找的缺點

1. 需要存儲在?持下標隨機訪問的結構中，并且有序
2. 插?和刪除數據效率很低。存儲在下標隨機訪問的結構中，插?和刪除數據?般需要挪動數據

這里二叉搜索樹的價值也更為顯著。

2.二叉搜索樹的實現

二叉搜索樹的核心功能是增、刪、查功能的實現，修改數據值的話主要會破壞搜索結構，進而大大降低效率，因此一般不會實現。下面會從邏輯->代碼依次實現各部分功能。

2.1創建

二叉搜索的底層結構還是一個鏈式二叉樹，因此需要結點，主體部分用根來連接各個結點即可。結點中需要儲存數據，以及左右孩子結點。但要注意的是搜索結構中顯示進行搜索的數據我們一般稱為關鍵字(key)。

其次結點的構造函數只需保證讓key值的構造，左右孩子指針置空即可。代碼如下：

#pragma once
#include<iostream>
using namespace std;//樹結點
template<class K>
struct BSTNode
{K _key;BSTNode<K>* _left;BSTNode<K>* _right;BSTNode(K x):_key(x),_left(nullptr),_right(nullptr){}
};//二叉搜索樹
template<class K>
class BSTree
{
private:typedef BSTNode<K> Node
public:private:Node* _root = nullptr;
};

2.2插入

插入分為為空插入與非空插入。當樹為空的時候只需讓根結點指向新結點即可。

當樹非空時，按照二叉搜索樹的性質，插入值比當前結點大就往右子樹走，插入值比當前結點小就往左子樹走。

當遇見插入值與當前結點相同時就可以直接返回，表示結構中已有此值。但為了區分void返回的插入成功與失敗，我們插入函數的返回類似設置為bool。

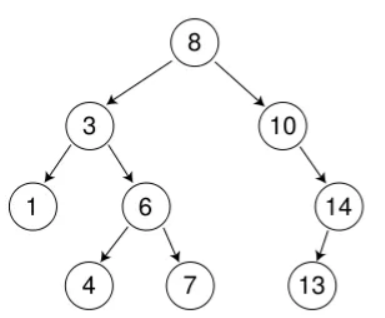
以在下圖樹中插入5為例：

????????????????????????????????????????

????????

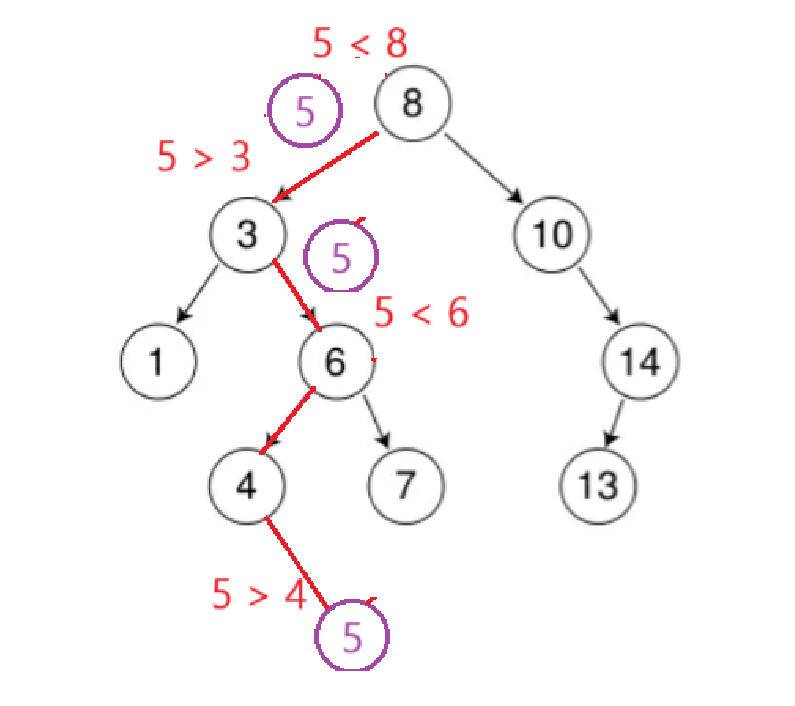
這里最需要注意的是最后一部得到5應該插入的位置時，那個位置是為空的，因此需要在過程中記錄應該插入位置的父結點。代碼如下：

//插入
bool insert(const K& key)
{//分為根為空或不為空if (_root == nullptr){_root = new Node(key);return true;}//不為空則尋找合適位置Node* cur = _root;Node* parent = nullptr;while (cur){parent = cur;if (key > cur->_key){cur = cur->_right;}else if (key < cur->_key){cur = cur->_left;}else if(key == cur->_key){return false; //不插入重復數據}}//插入左還是右if (key > parent->_key){parent->_right = new Node(key);}else{parent->_left = new Node(key);}return true;
}

除了迭代的方式插入，也可通過遞歸進行插入：

private://遞歸插入bool _insert(Node*& root, const K& x){if (root == nullptr){root = new Node(x);return true;}if (root->_key == x){return false;}return root->_key > x ? _insert(root->_left, x) : _insert(root->_right, x);}public://遞歸插入bool REinsert(const K& x){return _insert(_root, x);}

這里最值得注意的是遞歸插入利用引用特性，能直接修改最后空位置的結點。

2.3查找與遍歷

二叉搜索樹的查找邏輯與插入類似，不同的是遇見相同的值就返回當前結點，若樹遍歷完沒找到就返回空。但查找的前提是樹不為空。

二叉搜索樹的遍歷主要實現方式為中序遍歷，這部分主要注意的是在類中顯示成員函數實現遞歸，后面代碼實現后再進行分析。

private://方便函數內部傳參void _inorder(Node* root){if (root == nullptr){return;}_inorder(root->_left);cout << root->_key << ' ';_inorder(root->_right);}
public://遍歷——中序遍歷void inorder(){_inorder(_root);cout << endl;}//查找Node* find(const K& x){assert(_root != nullptr);Node* cur = _root;while (cur){if (cur->_key < x){cur = cur->_right;}else if (cur->_key > x){cur = cur->_left;}else if(cur->_key == x){return cur;}}return nullptr;}

?遞歸調用時因要傳參數，而在類外部無法直接傳樹的根結點，因此可以直接在類中進行內部函數嵌套，進而實現遞歸調用。

2.4刪除

二叉搜索樹的刪除是最復雜的，因為當結點刪除時可能也會涉及搜索結構的破壞，但這里的破壞情況會比修改簡單。

具體刪除情況可以分為以下三種(均以下圖樹為例)：

???????????????????????????????

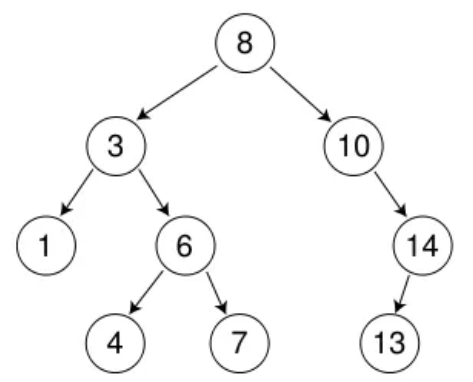
1.要刪除結點N左右孩?均為空。這時可以直接將改結點刪除，并將父節點置為空。

????????

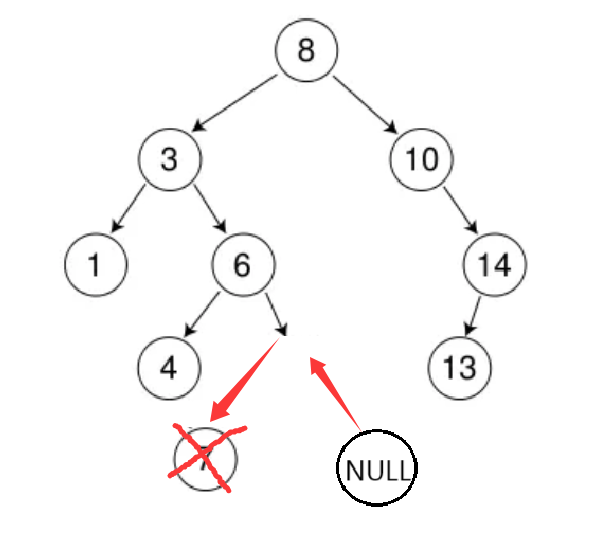
2.要刪除的結點N左孩?或右孩子為空，另一孩子結點不為空。這種情況下要刪改結點，可以直接讓該結點的父親指向該結點的孩子結點。

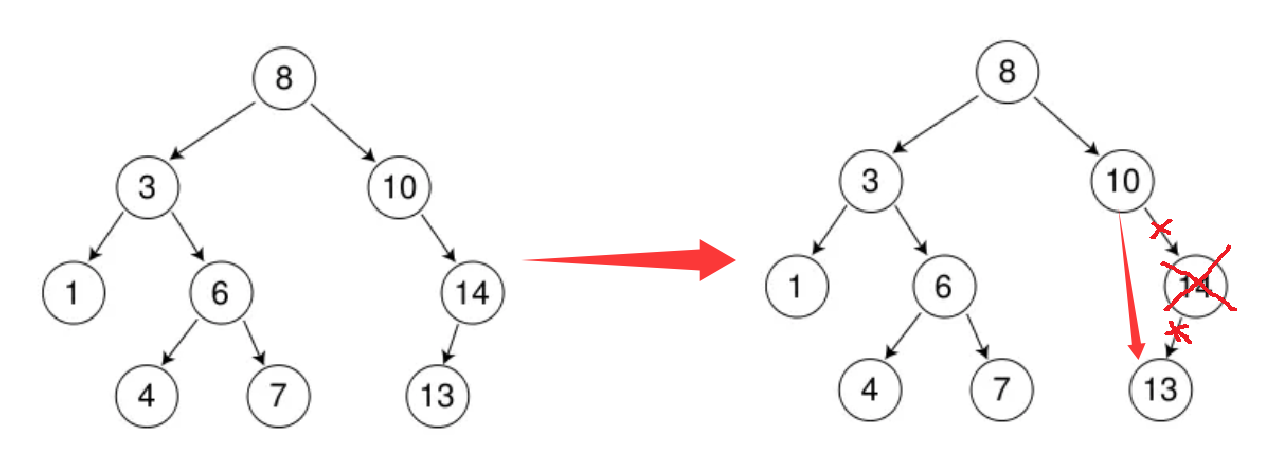
3.要刪除的結點N左右孩?結點均不為空。這種情況?法直接刪除N結點，因為N的兩個孩??處安放，只能?替換法刪除。找N左?樹的值最?結點R(最右結點)或者N右?樹的值最?結點R(最左結點)替代N，因為這兩個結點中任意?個，放到N的位置，都滿??叉搜索樹的規則。替代N的意思就是N和R的兩個結點的值交換，轉?變成刪除R結點，R結點符合情況2或情況3，可以直接刪除。

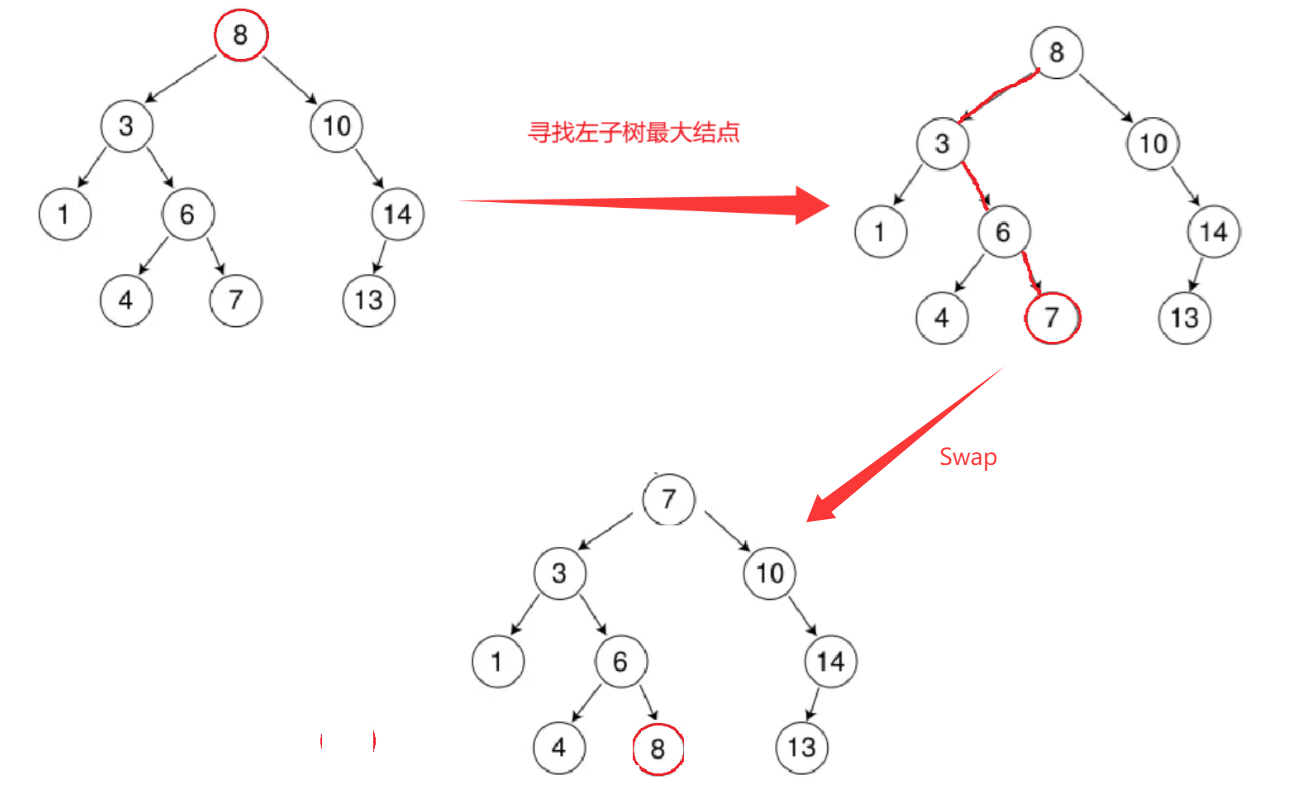
可以看到這里本質是讓其變為第一種情況再進行刪除。

綜上進行代碼實現：

public://刪除bool erase(const K& x){//內部查找Node* cur = _root;Node* parent = nullptr;while (cur){parent = cur;if (cur->_key < x){cur = cur->_right;}else if (cur->_key > x){cur = cur->_left;}else //找到了,進行分情況刪除{if(cur->_left == nullptr) //左孩子為空{if (cur != _root){//父親指向不為空的右if (cur == parent->_left){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}else{_root = cur->_right;}delete cur;}else if(cur->_right == nullptr) //右孩子為空{if (cur != _root){//父親指向不為空的右if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}else{_root = cur->_left;}delete cur;}else //左右都不為空{//查找合適結點——左子樹最大Node* curLeftmax = cur->_left;Node* maxParent = cur;while (curLeftmax->_right){maxParent = curLeftmax;curLeftmax = curLeftmax->_right;}//交換key值swap(cur->_key, curLeftmax->_key);if (curLeftmax == maxParent->_left)maxParent->_left = curLeftmax->_right;elsemaxParent->_right = curLeftmax->_right;delete curLeftmax;}return true;}}return false;}

這里實際情況并沒有將第一種分化出來，因為當被刪除結點的孩子都為空時，其父親無論指向左孩子還是右孩子仍然同樣置空。

其次是最后一種情況只交換兩個結點的值，不用再進行復雜的結點遷移，利于直接保持原樹順序。

3.二叉搜索樹類代碼

#pragma once
#include<iostream>
#include<assert.h>
#include<algorithm>
using namespace std;//樹結點
template<class K>
struct BSTNode
{K _key;BSTNode<K>* _left;BSTNode<K>* _right;BSTNode(K x):_key(x),_left(nullptr),_right(nullptr){}
};//二叉搜索樹
template<class K>
class BSTree
{
private:typedef BSTNode<K> Node;//方便函數內部傳參void _inorder(Node* root){if (root == nullptr){return;}_inorder(root->_left);cout << root->_key << ' ';_inorder(root->_right);}//遞歸插入bool _insert(Node*& root, const K& x){if (root == nullptr){root = new Node(x);return true;}if (root->_key == x){return false;}return root->_key > x ? _insert(root->_left, x) : _insert(root->_right, x);}public:BSTree() = default;//調用默認構造即可//插入bool insert(const K& key){//分為根為空或不為空if (_root == nullptr){_root = new Node(key);return true;}//不為空則尋找合適位置Node* cur = _root;Node* parent = nullptr;while (cur){parent = cur;if (key > cur->_key){cur = cur->_right;}else if (key < cur->_key){cur = cur->_left;}else if(key == cur->_key){return false; //不插入重復數據}}if (key > parent->_key){parent->_right = new Node(key);}else{parent->_left = new Node(key);}return true;}//遞歸插入bool REinsert(const K& x){return _insert(_root, x);}//刪除bool erase(const K& x){//內部查找Node* cur = _root;Node* parent = nullptr;while (cur){parent = cur;if (cur->_key < x){cur = cur->_right;}else if (cur->_key > x){cur = cur->_left;}else //找到了,進行分情況刪除{if(cur->_left == nullptr) //左孩子為空{if (cur != _root){//父親指向不為空的右if (cur == parent->_left){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}else{_root = cur->_right;}delete cur;}else if(cur->_right == nullptr) //右孩子為空{if (cur != _root){//父親指向不為空的右if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}else{_root = cur->_left;}delete cur;}else //左右都不為空{//查找合適結點——左子樹最大Node* curLeftmax = cur->_left;Node* maxParent = cur;while (curLeftmax->_right){maxParent = curLeftmax;curLeftmax = curLeftmax->_right;}//交換key值swap(cur->_key, curLeftmax->_key);if (curLeftmax == maxParent->_left)maxParent->_left = curLeftmax->_right;elsemaxParent->_right = curLeftmax->_right;delete curLeftmax;}return true;}}return false;}//遍歷——中序遍歷void inorder(){_inorder(_root);cout << endl;}//查找Node* find(const K& x){assert(_root != nullptr);Node* cur = _root;while (cur){if (cur->_key < x){cur = cur->_right;}else if (cur->_key > x){cur = cur->_left;}else if(cur->_key == x){return cur;}}return nullptr;}private:Node* _root = nullptr;
};

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/web/92765.shtml
繁體地址，請注明出處：http://hk.pswp.cn/web/92765.shtml
英文地址，請注明出處：http://en.pswp.cn/web/92765.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

基于Spring Boot和SSE的實時消息推送系統

基于Spring Boot和SSE的實時消息推送系統

一、SSE技術深度解析 1.1 協議工作原理 #mermaid-svg-u7ZBlEsXcn68R5a8 {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-u7ZBlEsXcn68R5a8 .error-icon{fill:#552222;}#mermaid-svg-u7ZBlEsXcn68R5a8 .error-text{fi…
閱讀更多...
Day 40 訓練和測試的規范寫法

Day 40 訓練和測試的規范寫法

知識點回顧&#xff1a; 彩色和灰度圖片測試和訓練的規范寫法&#xff1a;封裝在函數中展平操作&#xff1a;除第一個維度batchsize外全部展平dropout操作&#xff1a;訓練階段隨機丟棄神經元&#xff0c;測試階段eval模式關閉dropout 作業&#xff1a;仔細學習下測試和訓練代…
閱讀更多...
分析代碼并回答問題

分析代碼并回答問題

代碼 <template><div>Counter: {{ counter }}</div><div>Double Counter: {{ doubleCounter }}</div> </template><script setup lang"ts"> import { ref, computed } from "vue";const counter ref(0);const …
閱讀更多...
在macOS上掃描192.168.1.0/24子網的所有IP地址

在macOS上掃描192.168.1.0/24子網的所有IP地址

在macOS上掃描192.168.1.0/24子網的所有IP地址&#xff0c;可以通過終端命令實現。以下是幾種常用方法&#xff1a; 使用ping命令循環掃描 打開終端執行以下腳本&#xff0c;會逐個ping測試192.168.1.1到192.168.1.254的地址&#xff0c;并過濾出有響應的IP&#xff1a; for i …
閱讀更多...
Java基礎05——類型轉換(本文為個人學習筆記，內容整理自嗶哩嗶哩UP主【遇見狂神說】的公開課程。 ＞ 所有知識點歸屬原作者，僅作非商業用途分享）

Java基礎05——類型轉換(本文為個人學習筆記，內容整理自嗶哩嗶哩UP主【遇見狂神說】的公開課程。 ＞ 所有知識點歸屬原作者，僅作非商業用途分享）

Java基礎05——類型轉換 類型轉換 由于Java是強類型語言&#xff0c;所以要進行有些運算的時候&#xff0c;需要用到類型轉換。 如&#xff1a;byte(占1個字節)&#xff0c;short(占2個字節)&#xff0c;char(占2個字節)→int(4個字節)→long(占8個字節)→float(占4個字節)→do…
閱讀更多...
mysql基礎（二）五分鐘掌握全量與增量備份

mysql基礎（二）五分鐘掌握全量與增量備份

全量備份 Linux環境 數據備份 數據庫的備份與恢復有多中方法&#xff0c;通過mysql自帶的mysqldump工具可對數據庫進行備份。語法&#xff1a; mysqldump -u username -p password --databases db_name > file_name .sql說明&#xff1a; -u參數指定用戶名&#xff0c;usern…
閱讀更多...
使用Windbg分析多線程死鎖項目實戰問題分享

使用Windbg分析多線程死鎖項目實戰問題分享

目錄 1、問題描述 2、使用.effmach x86命令切換到32位上下文 3、切換到UI線程&#xff0c;發現UI線程死鎖了 4、使用!locks命令查看臨界區鎖的詳細信息&#xff0c;遇到了問題 5、使用dt命令查看臨界區對象信息&#xff0c;找到發生死鎖的多個線程 6、用戶態鎖與內核態鎖…
閱讀更多...
防火墻組網方式總結

防火墻組網方式總結

一、部署模式&#xff1a;靈活適配多樣網絡環境下一代防火墻&#xff08;NGAF&#xff09;具備極強的網絡適應能力&#xff0c;支持五種核心部署模式&#xff0c;可根據不同網絡需求靈活選擇。路由模式&#xff1a;防火墻相當于路由器&#xff0c;位于內外網之間負責路由尋址&a…
閱讀更多...
AI大模型：（二）5.1 文生視頻（Text-to-Video）模型發展史

AI大模型：（二）5.1 文生視頻（Text-to-Video）模型發展史

目錄 1.介紹 2.發展歷史 2.1.早期探索階段（2015-2019） 2.1.1.技術萌芽期 2.1.2.RNN/LSTM時代 2.2.技術突破期（2020-2021） 2.2.1 Transformer引入視頻生成 2.2.2 擴散模型的興起 2.3.商業化突破期（2022-2023） 2.3.1 產品化里程碑 2.3.2 競爭格局形成 2.4.革命…
閱讀更多...
14mm尋北儀能否塞進液壓支架生死縫隙？

14mm尋北儀能否塞進液壓支架生死縫隙？

在煤礦井下世界的方寸之間&#xff0c;液壓支架的每個關鍵節點都承載著千鈞重壓。頂梁鉸接點、立柱頂端、掩護梁角落&#xff0c;恰恰是空間最為局促的“禁區”。ER-MNS-10A MEMS尋北儀應運而生&#xff01;它采用了先進的MEMS陀螺技術&#xff0c;以14mm至薄高度、40g極致輕盈…
閱讀更多...
python之淺拷貝深拷貝

python之淺拷貝深拷貝

文章目錄潛拷貝(shallow copy)深拷貝(deep copy)總結一下python的淺拷貝和深拷貝.潛拷貝(shallow copy) python中潛拷貝指的是:構造一個新的復合對象&#xff0c;然后將原對象中的對象引用插入其中 平常開發過程中潛拷貝是比深拷貝更常見的場景. 比如編程中使用到的一些基本的…
閱讀更多...
普通大學本科生如何入門強化學習？

普通大學本科生如何入門強化學習？

問題:你平時是如何緊跟大型語言模型和智能體技術前沿的&#xff1f;有哪些具體的學習和跟蹤方式&#xff1f;回答:我會通過“輸入-內化-實踐”結合的方式跟蹤前沿。首先&#xff0c;學術動態方面&#xff0c;每天花10分鐘瀏覽arXiv的http://cs.CL和http://cs.AI板塊&#xff0c…
閱讀更多...
新手向:Python實現數據可視化圖表生成

新手向:Python實現數據可視化圖表生成

Python數據可視化入門&#xff1a;從零開始生成圖表數據可視化是數據分析過程中不可或缺的關鍵環節&#xff0c;它通過將抽象的數字信息轉化為直觀的圖形展示&#xff0c;幫助分析師和決策者更快速、更準確地發現數據中隱藏的模式、規律和發展趨勢。在當今大數據時代&#xff0…
閱讀更多...
VBA即用型代碼手冊：計算選擇的單詞數Count Words in Selection

VBA即用型代碼手冊：計算選擇的單詞數Count Words in Selection

我給VBA下的定義&#xff1a;VBA是個人小型自動化處理的有效工具。可以大大提高自己的勞動效率&#xff0c;而且可以提高數據的準確性。我這里專注VBA,將我多年的經驗匯集在VBA系列九套教程中。作為我的學員要利用我的積木編程思想&#xff0c;積木編程最重要的是積木如何搭建及…
閱讀更多...
DNS（域名系統）

DNS（域名系統）

分層結構根域名&#xff08;ipv4&#xff0c;13臺&#xff09;&#xff0c;二級域名&#xff0c;三級域名……相關記錄A將域名解析為ipv4地址AAAA將域名解析為ipv6地址MX指名該區域為郵件服務區PTR反向查詢將主機名解析為域名NS記錄服務器的名字CNAME別名查詢方式遞歸查詢迭代查…
閱讀更多...
【大模型】強化學習算法總結

【大模型】強化學習算法總結

角色和術語定義 State&#xff1a;狀態Action&#xff1a;動作Policy/actor model&#xff1a;策略模型&#xff0c;用于決策行動的主要模型Critic/value model&#xff1a;價值模型&#xff0c;用于評判某個行動的價值大小Reward model&#xff1a;獎勵模型&#xff0c;用于給…
閱讀更多...
基于梅特卡夫定律的開源鏈動2+1模式AI智能名片S2B2C商城小程序價值重構研究

基于梅特卡夫定律的開源鏈動2+1模式AI智能名片S2B2C商城小程序價值重構研究

摘要&#xff1a;梅特卡夫定律揭示了網絡價值與用戶數量的平方關系&#xff0c;在互聯網經濟中&#xff0c;連接的深度與形式正因人的參與發生質變。本文以開源鏈動21模式、AI智能名片與S2B2C商城小程序的協同應用為研究對象&#xff0c;通過實證分析其在社群團購、下沉市場等場…
閱讀更多...
Ubuntu22.04安裝CH340驅動及串口

Ubuntu22.04安裝CH340驅動及串口

一、CH340驅動安裝 1.1 查看USB設備能否被識別 CtrlAltT打開終端&#xff1a; lsusb 插入設備前&#xff1a; 插入設備后&#xff1a; 輸出中包含ID 1a86:7523 QinHeng Electronics CH340 serial converter的信息&#xff0c;這表明CH340設備已經被系統識別。 1.2 查看USB轉串…
閱讀更多...
CPU緩存（CPU Cache）和TLB（Translation Lookaside Buffer）緩存現代計算機體系結構中用于提高性能的關鍵技術

CPU緩存（CPU Cache）和TLB（Translation Lookaside Buffer）緩存現代計算機體系結構中用于提高性能的關鍵技術

CPU緩存&#xff08;CPU Cache&#xff09;和TLB&#xff08;Translation Lookaside Buffer&#xff09;緩存是現代計算機體系結構中用于提高性能的關鍵技術。它們通過減少CPU訪問數據和指令的延遲來提高系統的整體效率。以下是對這兩者的詳細解釋&#xff1a; 1. CPU 緩存 CPU…
閱讀更多...
唐揚·高并發系統設計40問

唐揚·高并發系統設計40問

課程下載&#xff1a;https://download.csdn.net/download/m0_66047725/91644703 00開篇詞 _ 為什么你要學習高并發系統設計&#xff1f;.pdf 00開篇詞丨為什么你要學習高并發系統設計&#xff1f;.mp3 01 _ 高并發系統&#xff1a;它的通用設計方法是什么&#xff1f;.pdf …
閱讀更多...
最新文章

Copyright @ 2022~2023