題目

給定一個無序的數組 nums，返回 數組在排序之后，相鄰元素之間最大的差值 。如果數組元素個數小于 2，則返回 0 。

您必須編寫一個在「線性時間」內運行并使用「線性額外空間」的算法。

思路

這道題的思路很簡單我們使用合適的排序方法后就可以很順利的找到最大差值了，那么關鍵是合法的排序方法是什么？我們常見的排序有：快排，歸并，希爾，堆排等等。題目要求我們的時間復雜度和空間復雜度都是O(N)，那么有哪些排序是可以完成這個要求的呢？下圖是常見的排序的時間復雜度和空間復雜度。

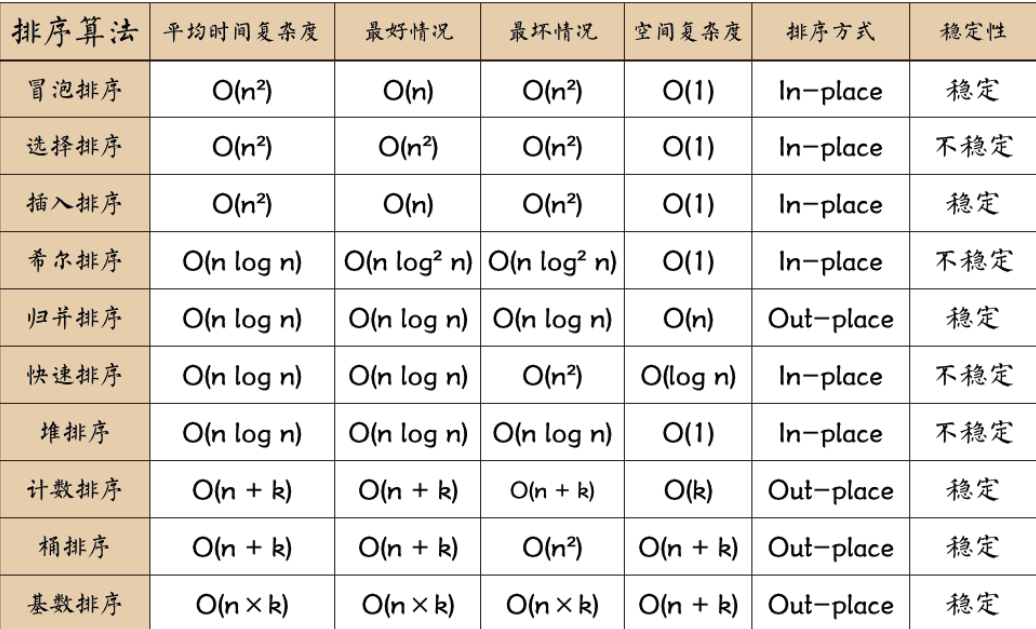
我們發現只有桶排序和基數排序是符合這個要求的但是桶排序在最壞的情況下還有可能達到O(N^2)。所以我們使用基數排序來完成。

代碼

class Solution {
public:int maximumGap(vector<int>& nums) {int n = nums.size();if (n < 2) {return 0;}else if(n == 2){return abs(nums[1] - nums[0]);}// 尋找最大值也就是知道有幾位數int maxval = *max_element(nums.begin(),nums.end());vector<int> res(n);long exp = 1;while (maxval >= exp) {// 十個桶vector<int> cnt(10);// 判斷每個桶里有幾個數for (int i = 0; i < n; i++) {int dig = (nums[i] / exp) % 10;cnt[dig]++;}// 將桶中存儲的幾個數轉換為每個桶里數的下標// 也就是桶中的數前面有幾個數for (int i = 1; i < 10; i++) {cnt[i] += cnt[i - 1];}// 將原數組的數按照順序來放到新數組中for (int i = n - 1; i >= 0; i--) {int dig = (nums[i] / exp) % 10;res[cnt[dig] - 1] = nums[i];cnt[dig]--;}copy(res.begin(),res.end(),nums.begin());exp *= 10;}int maxdiff = 0;for(int i = 1; i < n;i++){maxdiff = max(maxdiff,nums[i] - nums[i-1]);}return maxdiff;}
};