一: 一些基本概念
1.1 信息量:特定事件所攜帶的信息多少
信息量衡量的是特定事件所攜帶的信息多少,其數學定義為:其中p(x)是事件x發生的概率。
核心思想:越罕見的事件,其攜帶的信息量越大;越常見的事件,其攜帶的信息量越小。
例如:
- 如果某事件必然發生(p(x)=1),信息量為0,意味著觀察到它不會帶來任何新信息
-如果某事件極其罕見(p(x)很小),信息量很大,觀察到它提供了大量信息
1.2 驚奇度:觀察到某事件時的"意外程度"
驚奇度表示觀察到某事件時的"意外程度",其數學定義為:
核心思想:越意外的事件驚奇度越高,越預期的事件驚奇度越低。
實際上,驚奇度和信息量是完全等價的數學表達式:
信息量強調的是事件所攜帶的信息內容
驚奇度強調的是事件發生的意外程度
1.3 熵 Entropy:度量隨機變量的不確定性
信息論中的基本概念,用于度量隨機變量(一個概率分布)的不確定性。
熵的概念可以從信息論角度推導:
- 定義信息量: 對于概率為 p 的事件,其信息量為 I( p )=-log2 ( p)
- 低概率事件攜帶更多信息(更"意外")
- 高概率事件攜帶更少信息(更"預期")
1.3.1 定義:熵是平均信息量
熵是平均信息量:
對于離散隨機變量X,其熵定義為:
對于一個特例,p(X=x?)=1,即隨機變量 X 確定性地取值為 x?,我們可以如下推導:
所以,p(X=x?)=1表示隨機變量 X 是一個確定性變量,它總是取值為 x?,沒有任何不確定性。這種情況下:
– 隨機變量沒有任何隨機性
– 系統處于完全確定的狀態
– 我們可以100%確定 X 的值熵為0正是反映了這種情況:當系統完全確定(無不確定性)時,熵達到最小值0,不需要任何額外信息就能預測其狀態。
二元分布的熵與概率 p
- 橫軸是第一個事件發生的概率 p(第二個事件的概率就是 1-p)
- 縱軸是對應的熵值
- 這個圖會呈現出一個倒U形曲線,
- 在 p = 0.5 處達到最大值1比特。這是因為:
當 p 接近 0 或 1 時,分布非常不平衡,一個事件幾乎必然發生,另一個幾乎不可能發生,這種情況下熵接近于0(表示低不確定性)
當 p = 0.5 時,兩個事件等可能發生,這是最不確定的情況,熵達到最大值1比特
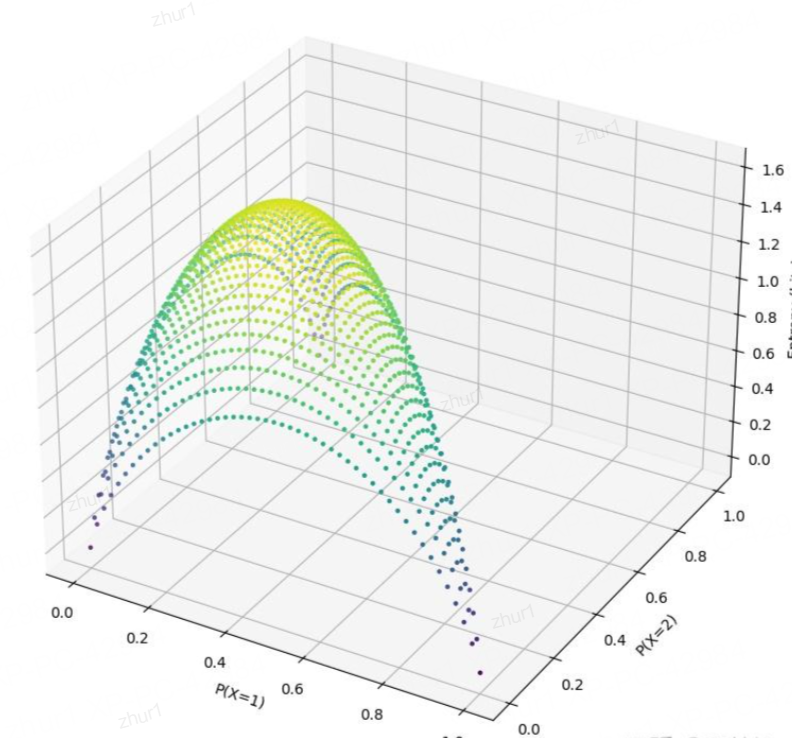
三元分布belike:
- 當分布均勻時(p1=p2=p3=1/3),熵達到最大值 log?(3) ≈ 1.585 比特
- 當一個概率接近1,其他接近0時,熵接近0
- 當兩個概率相等且較大,第三個較小時,熵介于log?(2)和log?(3)之間
- 分布越不均勻,熵值越低,表示不確定性越小
自由度解釋:
三元分布有兩個自由度時:
在一個有n個可能取值的概率分布中,因為所有概率之和必須等于1(∑p_i = 1),所以只有(n-1)個概率值可以自由選擇。一旦確定了這(n-1)個值,最后一個值就被約束了。
例如:
二元分布:只有1個自由度。如果p? = 0.3,那么必然p? = 0.7
三元分布:有2個自由度。如果p? = 0.2,p? = 0.5,那么必然p? = 0.3
1.3.2 熵 Entropy和期望 Expectation
期望是隨機變量的平均值或加權平均值,表示隨機變量的"中心位置"。
對于離散隨機變量 X,其期望定義為:
x 是隨機變量 X 可能的取值、p(x) 是 X 取值為 x 的概率
對于連續隨機變量 X,其期望定義為:
其中 f(x) 是 X 的概率密度函數。
推導過程
第一步:熵的標準定義
第二步:對數性質的應用
這一步是將負號移入對數內部,使用了對數的基本性質。
第三步:轉換為期望形式
這一步表明熵是隨機變量log(1/p(X))關于分布 p(x) 的期望。
熵是隨機變量 X的"驚奇度"log2(1/p(X))的平均值。
1/p(x) 越大(即概率越小),驚奇度越高,貢獻的信息量也越大。
熵是平均信息量 。換句話說,熵是對隨機變量不確定性的平均度量,數學上就是信息量的期望(期望值)
1.4 相對熵(KL散度)
KL散度的定義:
對于未知概率分布p(x),我們用q(x)去逼近p(x),并定義相對熵或稱KL散度。
1.5 交叉熵 Cross Entropy:度量兩個概率分布之間的差異
交叉熵定義:用于度量兩個概率分布之間的差異
所以可以得到
這個公式可以從編碼理論角度理解:
- H( p) - 使用最優編碼方案(基于真實分布p)對來自分布p的數據進行編碼所需的平均比特數
- H(p,q) - 使用基于估計分布q的編碼方案對來自真實分布p的數據進行編碼所需的平均比特數
- D(p||q) - 使用分布q的編碼方案(而非最優編碼方案p)所導致的額外編碼成本
因此,這個公式表明:交叉熵 = 最優編碼長度 + 使用錯誤分布造成的額外成本
二:從機器學習訓練角度理解交叉熵與KL散度
2.1 模型訓練目標:
有監督學習中:H( p) 是固定的,等價于最小化 D(p||q)
目標:最小化 p 和 q 之間的差異
在有監督學習中:
H( p)是固定的(取決于真實數據分布)
我們試圖最小化H(p,q)(交叉熵損失)
這等價于最小化D(p||q)(KL散度)
p(x) 是數據的真實分布(由標簽定義)
q(x) 是模型預測的分布(模型輸出)
我們的目標是最小化 p 和 q 之間的差異
2.2 為什么使用交叉熵作為損失函數
最小化交叉熵等價于最大化對數似然
當我們使用交叉熵 H(p,q) 作為損失函數時:
我們實際上是在最小化 D(p||q),因為 H( p) 是固定的
最小化交叉熵等價于最大化對數似然(log-likelihood)
交叉熵容易計算,且梯度性質好
梯度下降最小化交叉熵,D(p||q)→0時,q→p
當我們通過梯度下降最小化交叉熵時:
我們在尋找能夠使模型分布q最接近真實分布p的參數
在訓練過程中,D(p||q)逐漸減小
理想情況下,當D(p||q)→0時,q→p,模型完美擬合數據
- 訓練開始時:
q分布與p分布差異大,D(p||q)值高, 交叉熵損失值大- 訓練進行中:
模型更新使q逐漸接近p, D(p||q)逐漸減小, 交叉熵損失逐漸降低
過擬合與正則化
如果模型過度專注于使訓練數據的D(p||q)→0,可能會導致過擬合
正則化技術可以理解為對模型分布q施加額外約束,防止其過度擬合訓練數據的p
2.3 具體例子
2.3.1 多分類問題
p 是one-hot編碼的真實標簽 [0,1,0,0,…]
q 是模型輸出的softmax概率 [0.1,0.7,0.05,…]
交叉熵損失: H(p,q) = -∑p(x)log q(x)
因為p是one-hot編碼,這簡化為: -log q(正確類別)
2.3.2 在語言模型訓練中
p是下一個token的真實分布
q是模型預測的下一個token的概率分布
最小化H(p,q)使模型預測分布盡可能接近真實分布
這種框架不僅解釋了為什么交叉熵是首選損失函數,還幫助我們理解模型訓練的本質:讓模型分布逐漸接近數據真實分布的過程。
它幫助我們讓模型分布q盡可能接近真實分布p,當q完全匹配p時,KL散度為0,交叉熵達到理論最小值H§ 。
2.4 最大似然估計 MLE
最大似然估計是統計學習的核心原理,
MLE的本質:找到一組參數使模型生成觀測數據的概率最大
基本概念
我們從真實但未知的數據分布 p_data(x) 中采樣得到數據集
每個樣本 x_i 都是獨立同分布(i.i.d.)的
目標是估計模型參數 θ,使得模型分布Pmodel (x; θ)最接近真實分布
2.4.1 推導過程解析:MLE與交叉熵
 這一步是對目標函數(也就是似然函數)取對數。這樣做的原因是:
這一步是對目標函數(也就是似然函數)取對數。這樣做的原因是:
- 對數是單調遞增函數,所以最大化一個函數和最大化這個函數的對數是等價的,不會改變最大值對應的參數θ
- 將乘積轉換為求和,計算上更加方便,特別是當我們需要計算導數時
- 避免數值計算中的下溢問題。直接計算很多小概率的乘積容易導致數值變得極小,超出計算機的表示范圍
當我們將 p_model(x; θ) 記為 q(x),將 p_data(x) 記為 p(x) 時:
這最后一步正是最小化交叉熵
2.4.2 MLE的與交叉熵的等價性,
最小化交叉熵也等價于最小化KL散度
- MLE的本質
找到一組參數使模型生成觀測數據的概率最大- 與交叉熵的等價性:
最大化似然等價于最小化真實分布與模型分布之間的交叉熵- 與KL散度的關系:
由于H(p,q) = H§ + D(p||q),而H§是常數,最小化交叉熵也等價于最小化KL散度- 實際應用:
這就是為什么在神經網絡等模型訓練中,我們使用交叉熵作為損失函數 - 它直接對應于最大似然估計原則
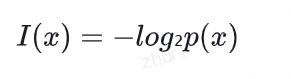
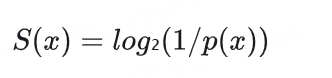
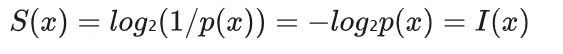
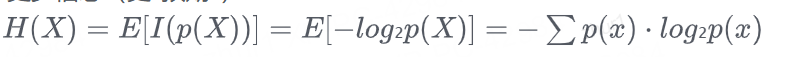
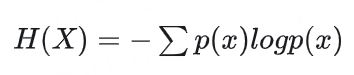
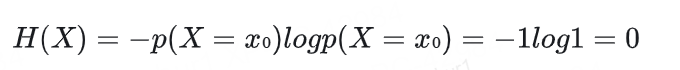
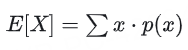
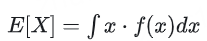
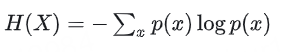
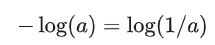
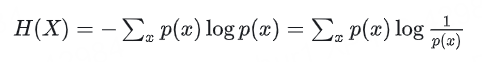
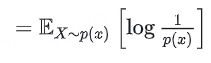

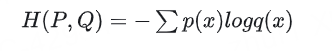
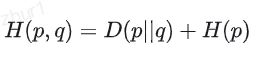
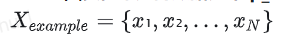
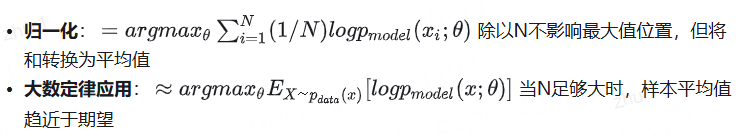
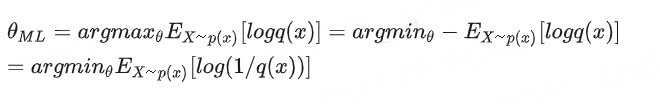
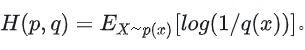

方法:從原理到并發控制實踐)






)
】)





![[Linux]從零開始的vs code交叉調試arm Linux程序教程](http://pic.xiahunao.cn/[Linux]從零開始的vs code交叉調試arm Linux程序教程)



