在機器學習領域,分類任務占據核心地位。Scikit-learn作為Python的機器學習利器,提供了豐富高效的分類算法。現在進行初步探討三種經典算法:K最近鄰(KNN)、樸素貝葉斯(Naive Bayes)和決策樹(Decision Tree),并延伸至集成方法隨機森林(Random Forest)
一、K最近鄰(KNN):基于實例的惰性學習
算法原理
KNN是一種典型的惰性學習(Lazy Learning) 算法。其核心思想是:相似的數據點擁有相似的標簽。預測新樣本時,算法在訓練集中找到與其最接近的K個鄰居,通過投票(分類)或平均(回歸)得出結果。
比如: 有10000個樣本,選出7個到樣本A的距離最近的,然后這7個樣本中假設:類別1有2個,類別2有3個,類別3有2個.那么就認為A樣本屬于類別2,因為它的7個鄰居中 類別2最多(近朱者赤近墨者黑)
再比如使用KNN算法預測《唐人街探案》電影屬于哪種類型?分別計算每個電影和預測電影的距離然后求解:
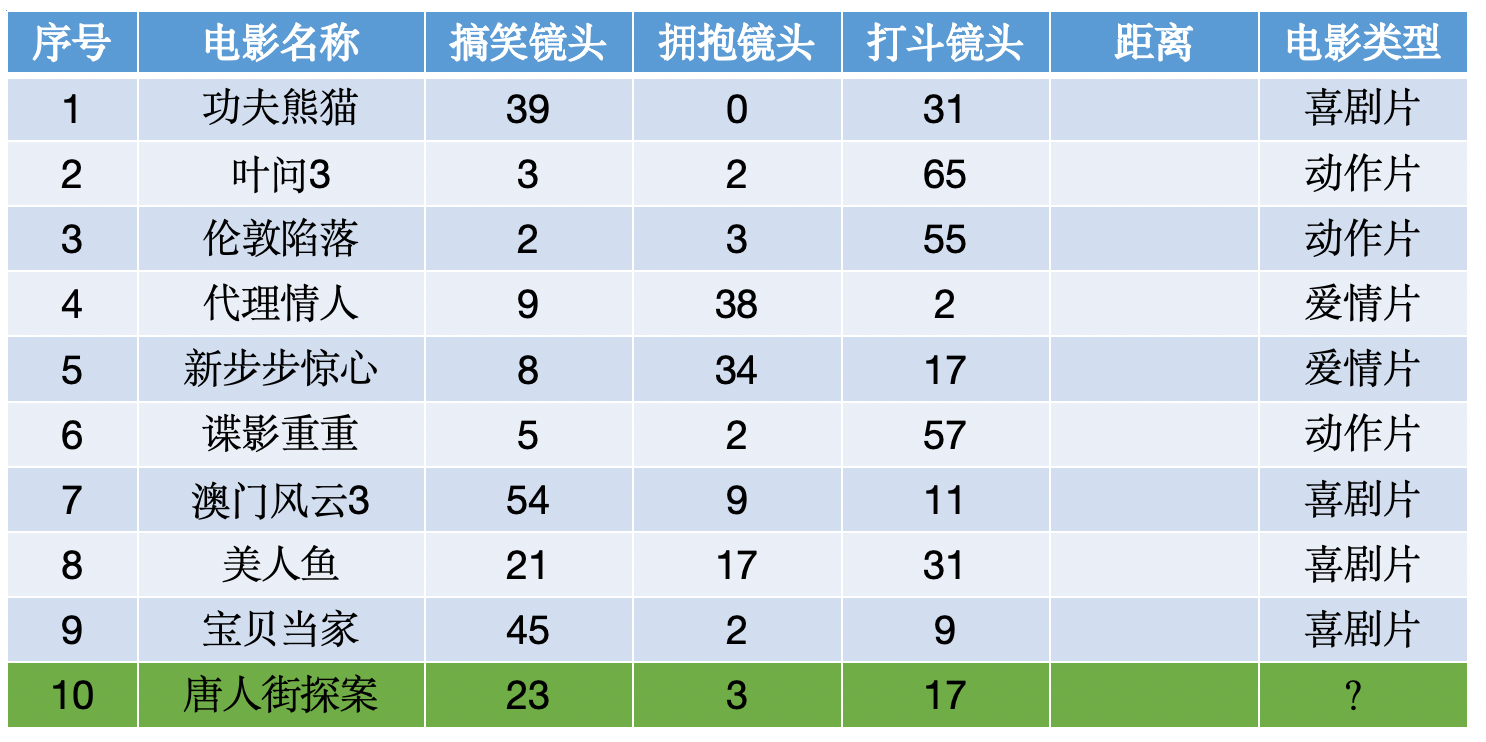
其中原理也很簡單,模型會通過給出的其余電影的每種鏡頭數量來計算唐探和每一個的距離,選出前k個電影,再綜合判斷唐探的類型。
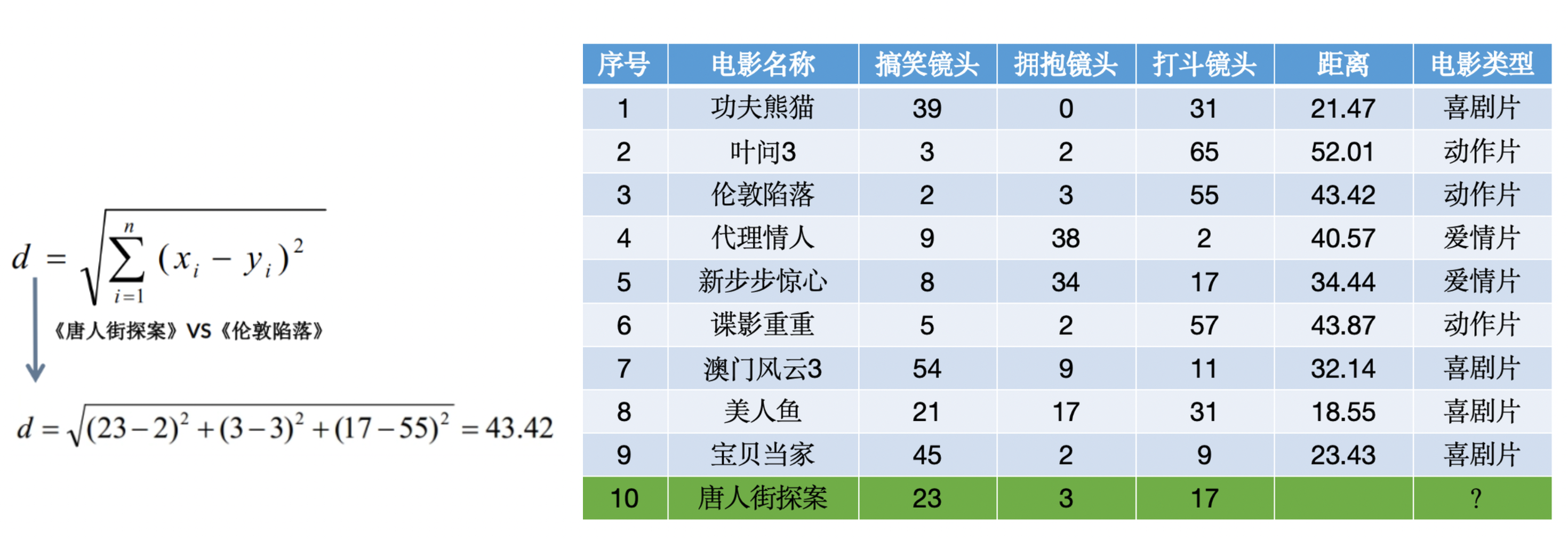
KNN算法API使用:
from sklearn.neighbors import KNeighborsClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split# 加載數據
iris = load_iris()
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.3)# 創建KNN模型(k=5,使用歐氏距離)
knn = KNeighborsClassifier(n_neighbors=5, metric='euclidean')
knn.fit(X_train, y_train)print("KNN準確率:", knn.score(X_test, y_test))
關鍵缺點與挑戰
- 計算成本高:預測時需計算新樣本與所有訓練樣本的距離,大數據集上效率低,使得KNN算法的訓練成本低,預測成本高。因為訓練只需要保存記錄訓練數據。
- 維度災難:高維空間中距離度量失效,分類性能急劇下降。簡而言之就是,當預測數據是極大的數據,如預測生物細胞特征差別等等,這一類數據往往特征差距數據量極大,當每一個樣本的差距都上億的,這種差距就沒有代表性。就好像你擁有馬爸爸的資產后掉了幾塊錢,幾十塊錢不會有多大心理波動。
- 特征縮放敏感:不同量綱的特征需標準化(如
StandardScaler)。 - 類別不平衡敏感:多數類易主導投票結果。
模型選擇與調優
- K值選擇:過小(k=1)導致過擬合、噪聲敏感;過大使決策邊界模糊。通過交叉驗證,超參數搜索選擇最優k:
from sklearn.model_selection import GridSearchCV param_grid = {'n_neighbors': range(1, 20)} grid_search = GridSearchCV(KNeighborsClassifier(), param_grid, cv=5) grid_search.fit(X_train, y_train) print("最優K值:", grid_search.best_params_['n_neighbors']) - 距離度量:歐氏距離(連續特征)、曼哈頓距離(高維)、余弦相似度(文本)等。
- 加速策略:使用
KDTree或BallTree數據結構(通過algorithm參數指定)。
二、樸素貝葉斯:概率推理的高效引擎
算法原理與貝葉斯推理
假設現在我們有一個數據集,它由兩類數據組成,數據分布如下圖所示: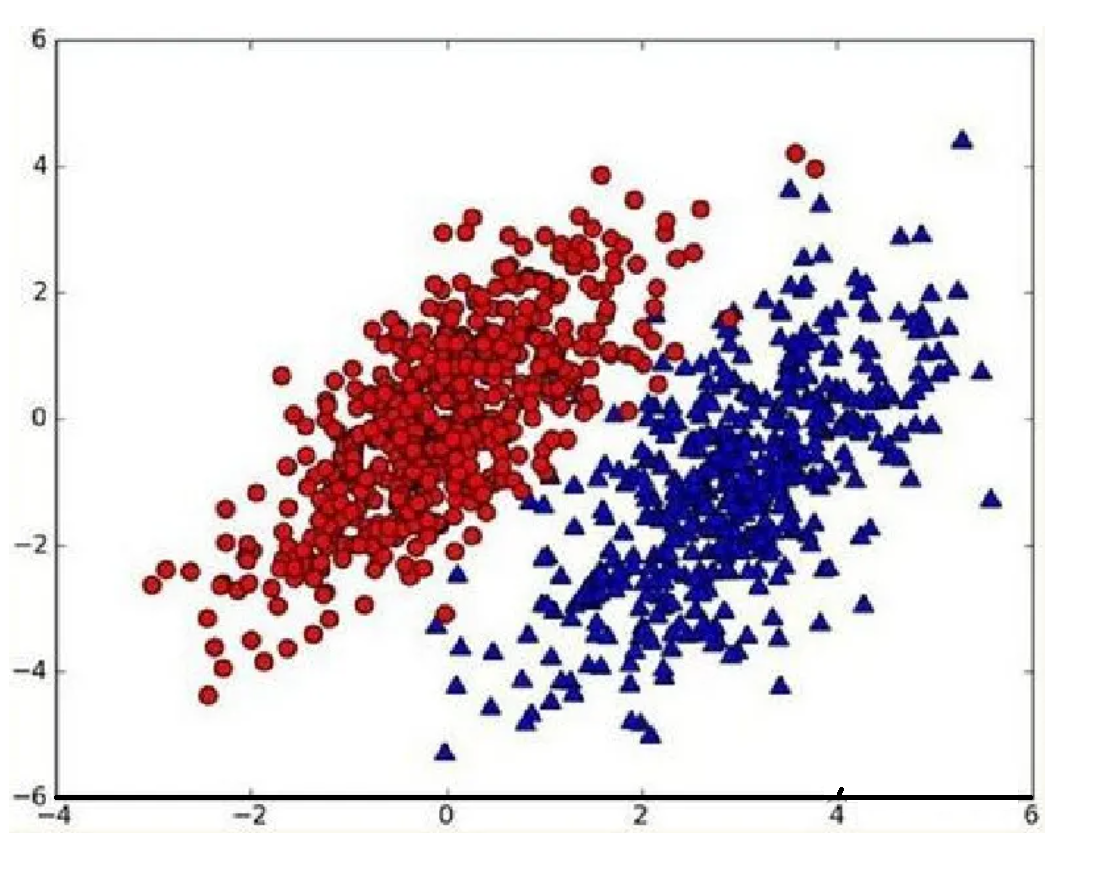
我們現在用p1(x,y)表示數據點(x,y)屬于類別1(圖中紅色圓點表示的類別)的概率,用p2(x,y)表示數據點(x,y)屬于類別2(圖中藍色三角形表示的類別)的概率,那么對于一個新數據點(x,y),可以用下面的規則來判斷它的類別:
- 如果p1(x,y)>p2(x,y),那么類別為1
- 如果p1(x,y)<p2(x,y),那么類別為2
也就是說,我們會選擇高概率對應的類別。這就是貝葉斯決策理論的核心思想,即選擇具有最高概率的決策。已經了解了貝葉斯決策理論的核心思想,那么接下來,就是學習如何計算p1和p2概率。
條件概率
在學習計算p1 和p2概率之前,我們需要了解什么是條件概率(Conditional probability),就是指在事件B發生的情況下,事件A發生的概率,用P(A|B)來表示。
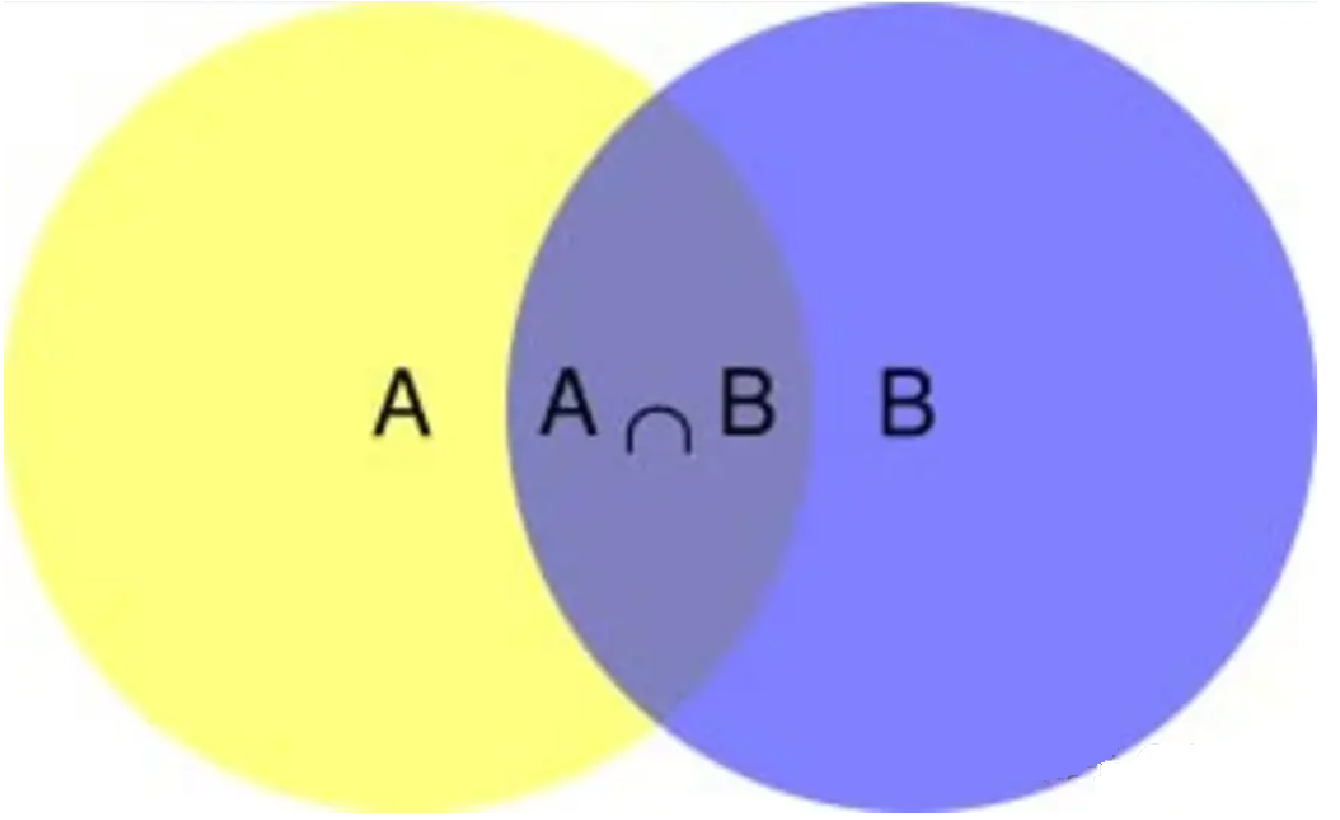
根據文氏圖,可以很清楚地看到在事件B發生的情況下,事件A發生的概率就是P(A∩B)除以P(B)。
𝑃(𝐴|𝐵)=𝑃(𝐴∩𝐵)/𝑃(𝐵)
因此,
𝑃(𝐴∩𝐵)=𝑃(𝐴|𝐵)𝑃(𝐵)
同理可得,
𝑃(𝐴∩𝐵)=𝑃(𝐵|𝐴)𝑃(𝐴)
即
𝑃(𝐴|𝐵)=𝑃(B|A)𝑃(𝐴)/𝑃(𝐵)
這就是條件概率的計算公式。
貝葉斯推斷
對條件概率公式進行變形,可以得到如下形式:
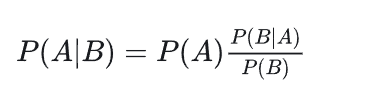
我們把P(A)稱為"先驗概率"(Prior probability),即在B事件發生之前,我們對A事件概率的一個判斷。
P(A|B)稱為"后驗概率"(Posterior probability),即在B事件發生之后,我們對A事件概率的重新評估。
P(B|A)/P(B)稱為"可能性函數"(Likelyhood),這是一個調整因子,使得預估概率更接近真實概率。
所以,條件概率可以理解成下面的式子:
后驗概率 = 先驗概率x調整因子
這就是貝葉斯推斷的含義。我們先預估一個"先驗概率",然后加入實驗結果,看這個實驗到底是增強還是削弱了"先驗概率",由此得到更接近事實的"后驗概率"。
樸素貝葉斯推斷
理解了貝葉斯推斷,那么讓我們繼續看看樸素貝葉斯。貝葉斯和樸素貝葉斯的概念是不同的,區別就在于“樸素”二字,樸素貝葉斯對條件概率分布做了條件獨立性的假設。 比如下面的公式,假設有n個特征:
根據貝葉斯定理,后驗概率 P(a|X) 可以表示為:
P(a∣X)=P(X∣a)P(a)P(X)P(a|X) = \frac{P(X|a)P(a)}{P(X)}P(a∣X)=P(X)P(X∣a)P(a)?
其中:
- P(X|a) 是給定類別 ( a ) 下觀測到特征向量 X=(x1, x2, …, xn) 的概率;
- P(a) 是類別 a 的先驗概率;
- P(X) 是觀測到特征向量 X 的邊緣概率,通常作為歸一化常數處理。
樸素貝葉斯分類器的關鍵假設是特征之間的條件獨立性,即給定類別 a ,特征 xix_ixi? 和 xjx_jxj? (其中 i≠ji \neq ji=j 相互獨立。)
因此,我們可以將聯合概率 P(X|a) 分解為各個特征的概率乘積:
P(X∣a)=P(x1,x2,...,xn∣a)=P(x1∣a)P(x2∣a)...P(xn∣a)P(X|a) = P(x_1, x_2, ..., x_n|a) = P(x_1|a)P(x_2|a)...P(x_n|a)P(X∣a)=P(x1?,x2?,...,xn?∣a)=P(x1?∣a)P(x2?∣a)...P(xn?∣a)
將這個條件獨立性假設應用于貝葉斯公式,我們得到:
P(a∣X)=P(x1∣a)P(x2∣a)...P(xn∣a)P(a)P(X)P(a|X) = \frac{P(x_1|a)P(x_2|a)...P(x_n|a)P(a)}{P(X)}P(a∣X)=P(X)P(x1?∣a)P(x2?∣a)...P(xn?∣a)P(a)?
這樣,樸素貝葉斯分類器就可以通過計算每種可能類別的條件概率和先驗概率,然后選擇具有最高概率的類別作為預測結果。
sklearn中的樸素貝葉斯分類器
- GaussianNB:假設連續特征服從高斯分布。
- MultinomialNB:適用于離散計數(如文本詞頻)。
- BernoulliNB:二值特征(如文本是否出現某詞)。
平滑系數(Laplace Smoothing)
解決零概率問題:當訓練集中某特征未在某個類中出現時,P(特征|類)=0會導致整個后驗概率為0。
平滑技術通過在計數中添加一個常數α(通常為1)避免此問題:
from sklearn.naive_bayes import MultinomialNB
from sklearn.feature_extraction.text import CountVectorizer# 文本分類示例
texts = ["good movie", "not good", "bad plot"]
y = [1, 0, 0] # 1:正面, 0:負面vectorizer = CountVectorizer()
X = vectorizer.fit_transform(texts)# 使用平滑系數alpha=1.0(默認)
nb = MultinomialNB(alpha=1.0)
nb.fit(X, y)test_text = ["good plot"]
test_X = vectorizer.transform(test_text)
print("預測類別:", nb.predict(test_X)) # 輸出: [1]
三、決策樹:直觀的規則生成器
決策樹的建立:核心是特征選擇
選擇最佳分裂特征以最大化數據“純度”提升。常用準則:
信息增益(Information Gain)
基于信息熵(Entropy):
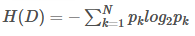
信息增益 = ![Entropy(父節點) - Σ[(|D?|/|D|) * Entropy(子節點?)]](https://i-blog.csdnimg.cn/direct/cb3fd1a5a43d484fa2066af99b560716.png)
偏向選擇取值較多的特征。
信息增益決策樹傾向于選擇取值較多的屬性,在有些情況下這類屬性可能不會提供太多有價值的信息,算法只能對描述屬性為離散型屬性的數據集構造決策樹。
根據以下信息構建一棵預測是否貸款的決策樹。我們可以看到有4個影響因素:職業,年齡,收入和學歷。
| 職業 | 年齡 | 收入 | 學歷 | 是否貸款 | |
|---|---|---|---|---|---|
| 1 | 工人 | 36 | 5500 | 高中 | 否 |
| 2 | 工人 | 42 | 2800 | 初中 | 是 |
| 3 | 白領 | 45 | 3300 | 小學 | 是 |
| 4 | 白領 | 25 | 10000 | 本科 | 是 |
| 5 | 白領 | 32 | 8000 | 碩士 | 否 |
| 6 | 白領 | 28 | 13000 | 博士 | 是 |
第一步,計算根節點的信息熵
上表根據是否貸款把樣本分成2類樣本,"是"占4/6=2/3, "否"占2/6=1/3,
所以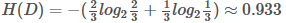
第二步,計算屬性的信息增益
<1> "職業"屬性的信息增益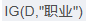
在職業中,工人占1/3, 工人中,是否代款各占1/2, 所以有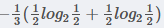
,
在職業中,白領占2/3, 白領中,是貸款占3/4, 不貸款占1/4, 所以有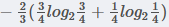
所以有 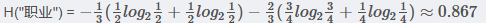
最后得到職業屬性的信息增益為:
<2>" 年齡"屬性的信息增益(以35歲為界)

<3> "收入"屬性的信息增益(以10000為界,大于等于10000為一類)
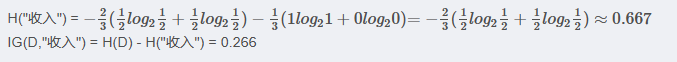
<4> "學歷"屬性的信息增益(以高中為界, 大于等于高中的為一類)
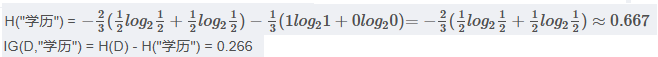
注意: 以上年齡使用35為界,收入使用10000為界,學歷使用高中為界,實計API使用中,會有一個參數"深度", 屬性中具體以多少為界會被根據深度調整。
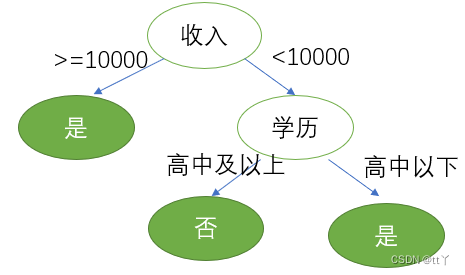
第三步, 劃分屬性
對比屬性信息增益發現,"收入"和"學歷"相等,并且是最高的,所以我們就可以選擇"學歷"或"收入"作為第一個
決策樹的節點, 接下來我們繼續重復1,2的做法繼續尋找合適的屬性節點
基于基尼指數決策樹的建立(了解)
基尼指數**(Gini Index)是決策樹算法中用于評估數據集純度的一種度量,基尼指數衡量的是數據集的不純度,或者說分類的不確定性。在構建決策樹時,基尼指數被用來決定如何對數據集進行最優劃分,以減少不純度。
基尼指數的計算
對于一個二分類問題,如果一個節點包含的樣本屬于正類的概率是 §,則屬于負類的概率是 (1-p)。那么,這個節點的基尼指數 (Gini§) 定義為:
Gini(p)=1?p2?(1?p)2=2p(1?p)Gini(p) = 1 - p^2 - (1-p)^2 = 2p(1-p)Gini(p)=1?p2?(1?p)2=2p(1?p)
對于多分類問題,如果一個節點包含的樣本屬于第 k 類的概率是 pkp_kpk?,則節點的基尼指數定義為:
Gini(p)=1?∑k=1Kpk2Gini(p) = 1 - \sum_{k=1}^{K} p_k^2Gini(p)=1?∑k=1K?pk2?
基尼指數的意義
- 當一個節點的所有樣本都屬于同一類別時,基尼指數為 0,表示純度最高。
- 當一個節點的樣本均勻分布在所有類別時,基尼指數最大,表示純度最低。
決策樹優點:
? 可視化 - 可解釋能力-對算力要求低
決策樹缺點:
? 易產生過擬合,所以不要把深度調整太大了。
決策樹API使用
class sklearn.tree.DecisionTreeClassifier(…)
參數:
criterion “gini” "entropy” 默認為=“gini”
當criterion取值為"gini"時采用 基尼不純度(Gini impurity)算法構造決策樹,
當criterion取值為"entropy”時采用信息增益( information gain)算法構造決策樹.
max_depth int, 默認為=None 樹的最大深度可視化決策樹
function sklearn.tree.export_graphviz(estimator, out_file=“iris_tree.dot”, feature_names=iris.feature_names)
參數:
estimator決策樹預估器
out_file生成的文檔
feature_names節點特征屬性名
功能:
把生成的文檔打開,復制出內容粘貼到"http://webgraphviz.com/"中,點擊"generate Graph"會生成一個樹型的決策樹圖
這里使用決策樹對sklearn本地分類數據集鳶尾花進行分類來作為實例:
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.tree import DecisionTreeClassifier, export_graphviz# 1)獲取數據集
iris = load_iris()# 2)劃分數據集
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)#3)標準化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)# 4)決策樹預估器
estimator = DecisionTreeClassifier(criterion="entropy")estimator.fit(x_train, y_train)# 5)模型評估,計算準確率
score = estimator.score(x_test, y_test)
print("準確率為:\n", score)# 6)預測
index=estimator.predict([[2,2,3,1]])
print("預測:\n",index,iris.target_names,iris.target_names[index])# 可視化決策樹
export_graphviz(estimator, out_file="iris_tree.dot", feature_names=iris.feature_names)
把文件"iris_tree.dot"內容粘貼到"http://webgraphviz.com/"點擊"generate Graph"決策樹圖
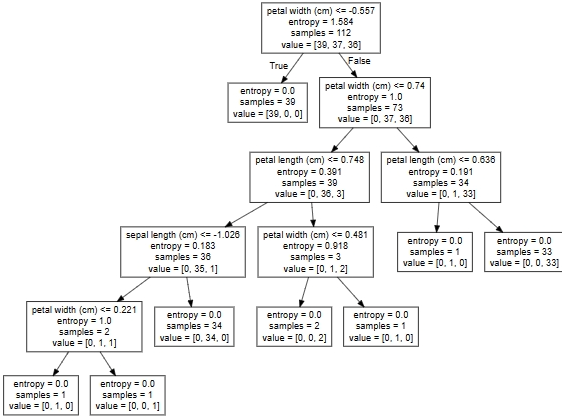
關鍵參數解析
max_depth:控制樹復雜度,防止過擬合的核心參數。min_samples_split/min_samples_leaf:限制節點繼續分裂的條件。ccp_alpha:代價復雜度剪枝參數(Post-pruning)。
四、集成學習之隨機森林:決策樹的威力升級
算法原理
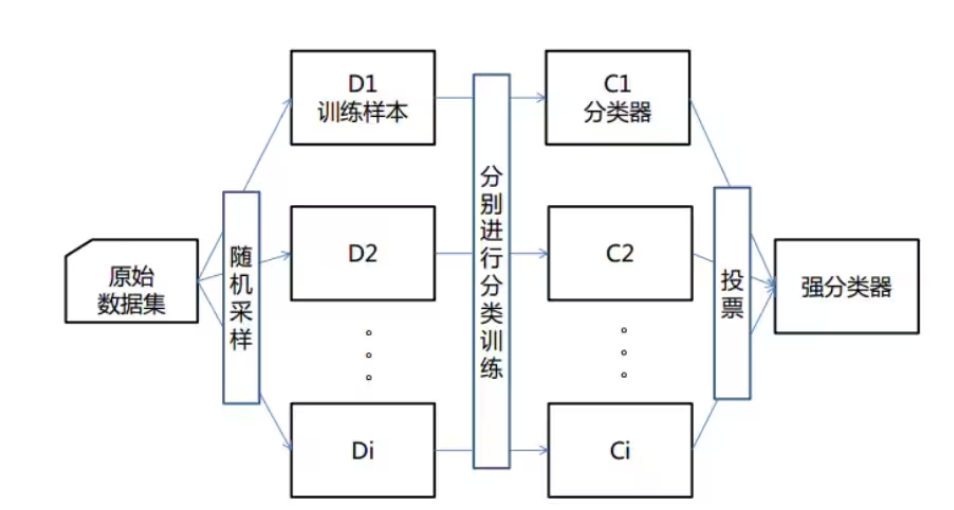
- 隨機: 特征隨機,訓練集隨機
- 樣本:對于一個總體訓練集T,T中共有N個樣本,每次有放回地隨機選擇n個樣本。用這n個樣本來訓練一個決策樹。
- 特征:假設訓練集的特征個數為d,每次僅選擇k(k<d)個來構建決策樹。
- 森林: 多個決策樹分類器構成的分類器, 因為隨機,所以可以生成多個決策樹
- 處理具有高維特征的輸入樣本,而且不需要降維
- 使用平均或者投票來提高預測精度和控制過擬合
核心思想
- Bagging(Bootstrap Aggregating):
從訓練集有放回隨機抽樣生成多個子集,分別訓練基模型。 - 隨機特征子空間:
每個決策樹分裂時,僅考慮隨機選取的一部分特征(如max_features='sqrt')。
為什么有效?
- 降低方差:通過平均多個獨立訓練的樹,減少模型對訓練數據的敏感度。
- 提高泛化能力:特征隨機性增加了模型的多樣性。
sklearn實現與優勢
from sklearn.ensemble import RandomForestClassifierrf = RandomForestClassifier(n_estimators=100, # 森林中樹的數量criterion='gini', # 分裂準則max_depth=None, # 樹可生長到最大深度(常不限制,靠其他參數剪枝)min_samples_split=2,min_samples_leaf=1,max_features='auto', # 通常為 'sqrt' (特征總數的平方根)bootstrap=True, # 使用bootstrap抽樣oob_score=True, # 使用袋外樣本評估模型n_jobs=-1, # 使用所有CPU核心random_state=42
)
rf.fit(X_train, y_train)print("袋外估計準確率:", rf.oob_score_)
關鍵優勢
- 顯著提升預測準確性(相比單棵決策樹)。
- 自帶特征重要性評估(
rf.feature_importances_)。 - 對部分特征缺失、異常值不敏感。
- 袋外樣本(OOB)提供內置驗證。
五、算法對比與選擇指南
| 特性 | KNN | 樸素貝葉斯 | 決策樹 | 隨機森林 |
|---|---|---|---|---|
| 學習類型 | 惰性學習 | 渴望學習 | 渴望學習 | 集成學習(渴望) |
| 訓練速度 | 快(無顯式訓練) | 非常快 | 快 | 較慢(需訓練多棵樹) |
| 預測速度 | 慢(需計算距離) | 快 | 快 | 中等(取決于樹數量) |
| 可解釋性 | 低 | 中等(概率) | 高(規則清晰) | 低(整體模型) |
| 對數據假設 | 無 | 強(特征獨立) | 無 | 無 |
| 處理高維數據 | 差(維度災難) | 好(文本分類表現佳) | 中等 | 好 |
| 抗噪聲/過擬合 | 敏感(需調k) | 穩健(依賴分布假設) | 易過擬合(需剪枝) | 強(Bagging+隨機) |
| 主要調優參數 | n_neighbors, metric | alpha (平滑系數) | max_depth, min_* | n_estimators, max_features |
場景推薦:
- 追求極致速度/文本分類:樸素貝葉斯(特別是
MultinomialNB)。 - 需要可解釋性/簡單規則:決策樹(
max_depth不宜過大)。 - 平衡精度與效率/通用場景:隨機森林(首選)。
- 小數據集/低維/需簡單基準:KNN(注意標準化和k選擇)。
結語
掌握KNN、樸素貝葉斯、決策樹及隨機森林的原理與實戰技巧,是構建高效分類系統的基石。理解算法背后的假設、優缺點及適用場景,結合Scikit-learn強大的API和調優工具(如GridSearchCV),能針對實際問題游刃有余地選擇與優化模型。沒有“最好”的算法,只有“最合適”的算法。持續探索不同模型在數據上的表現,是機器學習工程師的精進之道。
代碼實踐提示:本文所有代碼示例均基于
scikit-learn 1.3+版本,運行前請確保安裝正確依賴(pip install scikit-learn matplotlib)。可視化決策樹需額外安裝graphviz。


)

)




)









