一、線性回歸簡介
1.什么是線性回歸
線性回歸(Linear?? ?regression)是利?回歸?程(函數)對?個或多個?變量(特征值)和因變量(?標值)之間關系進?建模的?種分析?式。
特點:只有?個?變量的情況稱為單變量回歸,多于?個?變量情況的叫做多元回歸
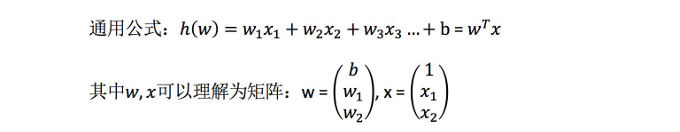 ?
?
?線性回歸?矩陣表示舉例:

線性回歸的特征與?標的關系分析?:
線性回歸當中主要有兩種模型,?種是線性關系,另?種是?線性關系。
二、線性回歸api初步使?
sklearn.linear_model.LinearRegression(fit_intercept=True)
通過正規?程優化
參數:fit_intercept:是否計算偏置
屬性:LinearRegression.coef_:回歸系數
LinearRegression.intercept_:偏置
sklearn.linear_model.SGDRegressor(loss="squared_loss",?? ?fit_intercept=True,?? ?learning_rate?? ?='invscaling',eta0=0.01)
SGDRegressor類實現了隨機梯度下降學習,它?持不同的loss函數和正則化懲罰項來擬合線性回歸模型。
參數:loss:損失類型
loss=”squared_loss”:?? ?普通最??乘法
fit_intercept:是否計算偏置
learning_rate?? ?:?? ?string,?? ?optional
學習率填充
'constant':?? ?eta?? ?=?? ?eta0
'optimal':?? ?eta?? ?=?? ?1.0?? ?/?? ?(alpha?? ?*?? ?(t?? ?+?? ?t0))?? ?[default]
'invscaling':?? ?eta?? ?=?? ?eta0?? ?/?? ?pow(t,?? ?power_t)
power_t=0.25:存在?類當中對于?個常數值的學習率來說,可以使?learning_rate=’constant’?? ?,并使?eta0來指定學習率。
屬性:
SGDRegressor.coef_:回歸系數
SGDRegressor.intercept_:偏置
三、線性回歸的損失和優化
1.損失函數
總損失定義為:
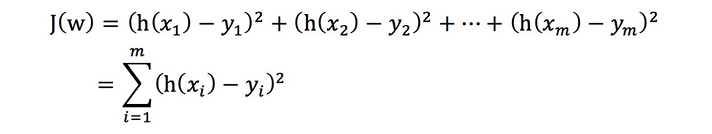
y 為第i個訓練樣本的真實值
h(x )為第i個訓練樣本特征值組合預測函數
?稱最??乘法
2.優化算法
如何去求模型當中的W,使得損失最??(?的是找到最?損失對應的W值)
線性回歸經常使?的兩種優化算法:1.正規?程? 2.梯度下降法
(1)?正規?程的推導
把該損失函數轉換成矩陣寫法:
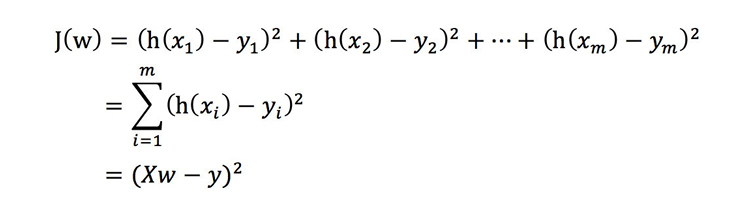
其中y是真實值矩陣,X是特征值矩陣,w是權重矩陣
對其求解關于w的最?值,起?y,X?? ?均已知?次函數直接求導,導數為零的位置,即為最?值。
求導:
?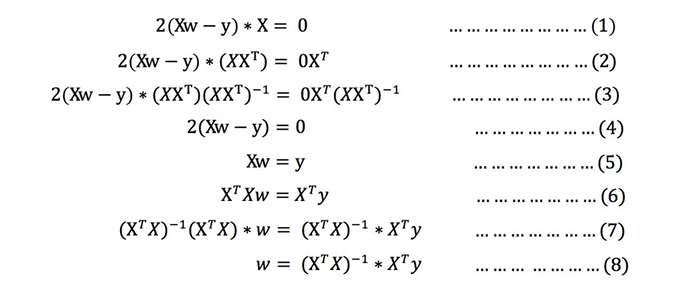
注:式(1)到式(2)推導過程中,?? ?X是?個m?n列的矩陣,并不能保證其有逆矩陣,但是右乘X 把其變成?個?陣,保證其有逆矩陣。
式(5)到式(6)推導過程中,和上類似。?
四、項目案列
1.問題背景
糖尿病是一種常見的慢性疾病,其病情發展與多種因素相關(如年齡、體重指數、血壓等)。本案例將通過線性回歸模型,探索這些因素與糖尿病病情進展的量化關系,實現對病情的預測。
2 數據介紹
輸入特征(10 個):age(年齡)、sex(性別)、bmi(體重指數)、bp(平均血壓)、s1-s6(6 項血清指標)
目標變量:target(一年后糖尿病病情進展的量化值)
數據已做標準化處理,可直接用于模型訓練。
3.完整流程實現:
1. 導入必要的庫
import pandas as pd # 用于數據讀取和處理
from sklearn.linear_model import LinearRegression # 導入線性回歸模型2. 讀取數據
data = pd.read_csv('糖尿病數據.csv', encoding='gbk')用pd.read_csv讀取 CSV 格式的糖尿病數據
?encoding='gbk'指定編碼格式,確保中文正常顯示(Windows 系統常見需求)
3. 計算相關性
corr = data[['age','sex','bmi','bp','s1','s2','s3','s4','s5','s6','target']].corr()選取數據中的 10 個特征和 1 個目標變量target
用corr()計算這些變量之間的相關系數,用于分析變量間的相關性強度
4. 定義特征和目標變量
x = data[['age','sex','bmi','bp','s1','s2','s3','s4','s5','s6']] # 特征變量
y = data[['target']] # 目標變量(一年后糖尿病病情進展)x包含 10 個輸入特征:年齡、性別、體重指數、血壓及 6 項血清指標
y是需要預測的目標變量:糖尿病病情進展的量化值
5. 構建并訓練線性回歸模型
lr_model = LinearRegression() # 初始化線性回歸模型
lr_model.fit(x, y) # 用特征x和目標變量y訓練模型LinearRegression()創建線性回歸模型實例
fit(x, y)通過最小二乘法擬合數據,求解最優回歸系數
6. 評估模型性能
score = lr_model.score(x, y) # 計算決定系數R2
print(f"模型決定系數(R2):{score}")score(x, y)計算模型的決定系數 R2,衡量模型對數據的擬合程度
R2 取值范圍為 [0,1],越接近 1 表示模型擬合效果越好
7. 準備預測數據并進行預測
# 構建帶特征名的預測數據(解決特征名匹配問題)
predict_data = pd.DataFrame([[0.00538306037424807, -0.044641636506989, -0.0363846922044735,0.0218723549949558, 0.00393485161259318, 0.0155961395104161,0.0081420836051921, -0.00259226199818282, -0.0319914449413559,-0.0466408735636482]],columns=['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']
)
print("預測結果:", lr_model.predict(predict_data)) # 輸出預測值將新樣本數據轉換為 DataFrame 并指定與訓練數據相同的特征名
predict(predict_data)使用訓練好的模型對新樣本進行預測,輸出糖尿病病情進展的預測值
8. 提取模型參數并構建回歸方程
coefficients = lr_model.coef_[0] # 提取特征系數(權重),轉換為一維數組
intercept = lr_model.intercept_[0] # 提取截距項,轉換為標量# 構建線性回歸方程表達式
features = ['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']
model_expression = "y = "
for i in range(len(coefficients)):model_expression += f"{coefficients[i]:.2f}x{i+1} + " # 拼接系數和特征編號
model_expression += f"{intercept:.2f}" # 拼接截距項print(f'線性回歸模型為:{model_expression}') # 輸出完整的回歸方程coef_[0]獲取 10 個特征對應的系數(權重),表示各特征對目標變量的影響程度intercept_[0]獲取回歸方程的截距項- 通過循環構建完整的線性回歸方程表達式,直觀展示各特征與目標變量的量化關系
完整代碼如下:
import pandas as pd
from sklearn.linear_model import LinearRegression
data=pd.read_csv('糖尿病數據.csv',encoding='gbk')
corr=data[['age','sex','bmi','bp','s1','s2','s3','s4','s5','s6','target']].corr()
x=data[['age','sex','bmi','bp','s1','s2','s3','s4','s5','s6']]
y=data[['target']]
lr_model=LinearRegression()
lr_model.fit(x,y)
score=lr_model.score(x,y)
print(f"模型決定系數(R2):{score}")
predict_data = pd.DataFrame([[0.00538306037424807, -0.044641636506989, -0.0363846922044735,0.0218723549949558, 0.00393485161259318, 0.0155961395104161,0.0081420836051921, -0.00259226199818282, -0.0319914449413559,-0.0466408735636482]],columns=['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6'])
print("預測結果:", lr_model.predict(predict_data))
coefficients = lr_model.coef_[0]
intercept = lr_model.intercept_[0]
features = ['age', 'sex', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']
model_expression = "y = "
for i in range(len(coefficients)):model_expression += f"{coefficients[i]:.2f}x{i+1} + "
model_expression += f"{intercept:.2f}"
print(f'線性回歸模型為:{model_expression}')
?代碼整體作用
通過線性回歸模型分析糖尿病數據中各醫學特征與病情進展的關系,構建可解釋的數學模型,并利用該模型對新患者的病情進展進行預測。代碼同時解決了特征名不匹配警告和系數格式化錯誤等常見問題,確保模型正常運行并輸出直觀的結果。



:基于 Qt Widgets 搭建串口調試界面)



)
)



)





)
