機器學習第二課之線性回歸的實戰技巧

1 線性回歸簡介

1 線性回歸應用場景

????????線性回歸是一種用于分析自變量與連續型因變量之間線性關系的模型，其核心是通過擬合線性方程(y = w_1x_1 + w_2x_2 + ... + w_nx_n + b）來預測因變量或解釋自變量的影響。由于其簡單、可解釋性強的特點，線性回歸在多個領域有廣泛應用。預測類場景（核心應用）包括房價預測、銷售額 / 銷量預測、能源消耗預測等。影響因素分析（解釋性應用）上包括經濟指標分析、醫學健康分析等都可以使用線性回歸算法進行預測。

?2.線性回歸的定義與公式

????????線性回歸 (Linear regression) 是利用回歸方程 (函數) 對一個或多個自變量 (特征值) 和因變量 (目標值) 之間關系進行建模的一種分析方式。這種函數是一個或多個稱為回歸系數的模型參數的線性組合。只有一個自變量的情況稱為簡單回歸，大于一個自變量情況的叫做多元回歸。（這反過來又應當由多個相關的因變量預測的多元線性回歸區別，而不是一個單一的標量變量。）在線性回歸中，數據使用線性預測函數來建模，并且未知的模型參數也是通過數據來估計。這些模型被叫做線性模型。最常用的線性回歸建模是給定X值的y的條件均值是X的仿射函數。不太一般的情況，線性回歸模型可以是一個中位數或一些其他的給定X的條件下y的條件分布的分位數作為X的線性函數表示。像所有形式的回歸分析一樣，線性回歸也把焦點放在給定X值的y的條件概率分布，而不是X和y的聯合概率分布（多元分析領域）。

特點：只有一個自變量的情況稱為單變量回歸，多于一個自變量情況的叫做多元回歸

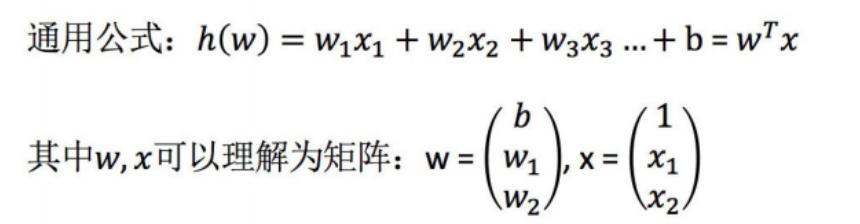
?那么怎么理解呢？我們來看幾個例子

期末成績：0.7× 考試成績 + 0.3× 平時成績
房子價格 = 0.02× 中心區域的距離 + 0.04× 城市一氧化氮濃度 + (-0.12× 自住房平均房價) + 0.254× 城鎮犯罪率

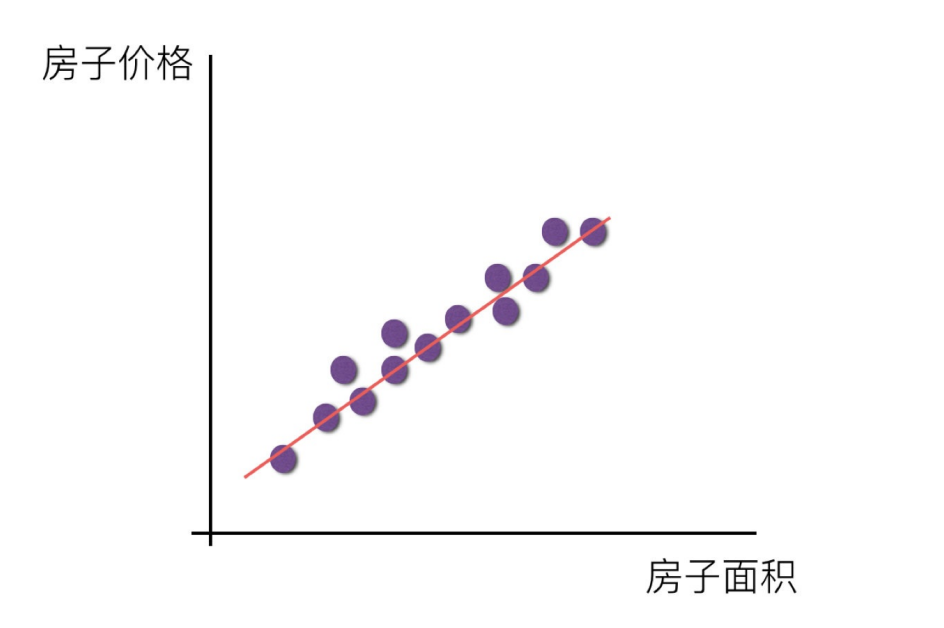
上面兩個例子，我們看到特征值與目標值之間建立了一個關系，這個關系可以理解為線性模型。

3.線性回歸的特征與?標的關系分析?

????????線性回歸當中主要有兩種模型，?種是線性關系，另?種是?線性關系。在這?我們只能畫?個平?更好去理解，所以都?單個特征或兩個特征舉例?。

????????線性關系

單變量線性關系：（一元線性回歸）

?y=mx+b

????????中學時，我們經常使用上面的方程來解一些數學問題，方程描述了變量?y?隨著變量?x?而變化。方程從圖形上來看，是一條直線。如果建立好這樣的數學模型，已知?x?我們就可以得到預測的 $\hat{y}$ 值了。統計學家給變量帶上了一個小帽子，表示這是預測值，以區別于真實觀測到的數據。方程只有一個自變量?x，且不含平方立方等非一次項，因此被稱為一元線性方程。?

????????在對收入數據集進行建模時，我們可以對參數?m?和?b?取不同值來構建不同的直線，這樣就形成了一個參數家族。參數家族中有一個最佳組合，可以在統計上以最優的方式描述數據集。那么監督學習的過程就可以被定義為：給定?N?個數據對?(x, y)，尋找最佳參數?m*和?b*，使模型可以更好地擬合這些數據。?

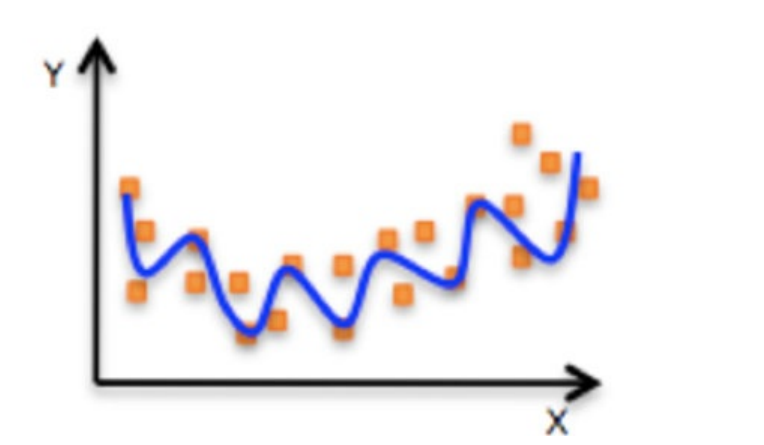
????????上圖給出了不同的參數，到底哪條直線是最佳的呢？如何衡量模型是否以最優的方式擬合數據呢？機器學習用損失函數（loss function）來衡量這個問題。損失函數又被稱為代價函數（cost function），它計算了模型預測值 $\hat{y}$ 和真實值?y?之間的差異程度。從名字也可以看出，這個函數計算的是模型犯錯的損失或代價，損失函數越大，模型越差，越不能擬合數據。統計學家通常使用$L(\hat{y}, y)$來表示損失函數。?

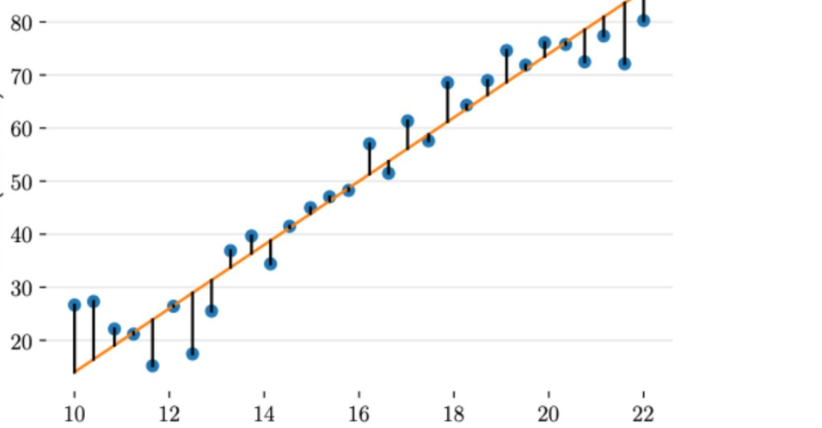
????????對于線性回歸，一個簡單實用的損失函數為預測值與真實值誤差的平方。上圖展示了收入數據集上預測值與真實值之間的誤差。

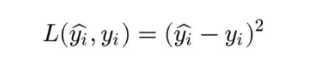
多變量線性關系?(多元線性回歸)

????????現在我們把?x?擴展為多元的情況，即多種因素共同影響變量?y。現實問題也往往是這種情況，比如，要預測房價，需要考慮包括是否學區、房間數量、周邊是否繁華、交通方便性等。共有?D?種維度的影響因素，機器學習領域將這?D?種影響因素稱為特征（feature）。每個樣本有一個需要預測的?y?和一組?D?維向量? $\mathbf{X}$ 。原來的參數?m?變成了?D?維的向量? $\mathbf{w}$ 。這樣，某個? $y_i$ 可以表示成? $b + \sum_{d=1}^{D} w_d x_{i,d}$ ，其中 $x_{i,d}$ 表示第?i?個樣本向量? $\mathbf{x}_i$ 中第?d?維特征值。

$y_i = b + \sum_{d=1}^{D} w_d x_{i,d} \qquad b = w_{D+1}\)\(y_i = \sum_{d=1}^{D+1} w_d x_{i,d}$ ?

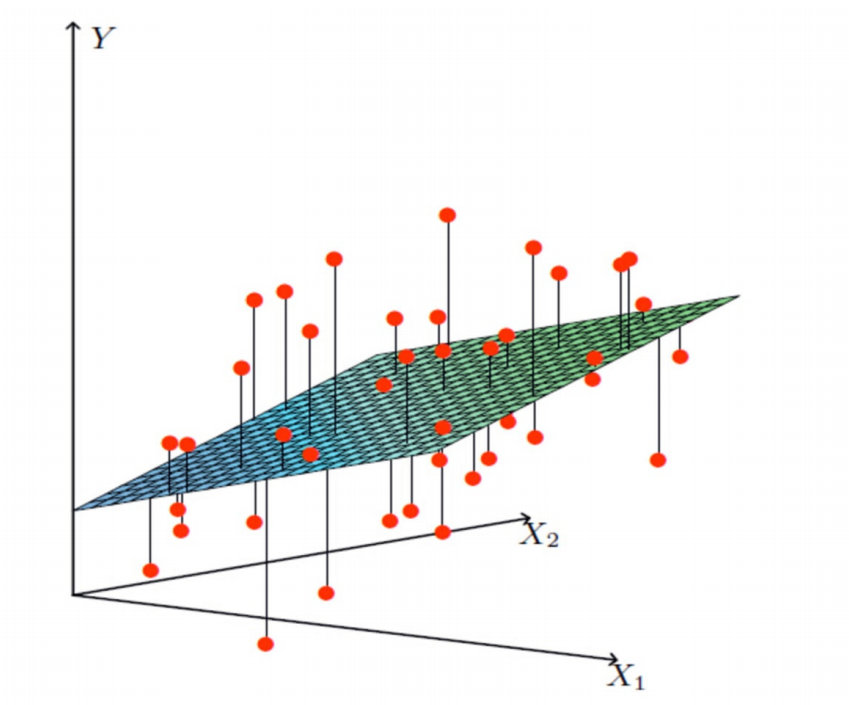
????????比一元線性回歸更為復雜的是，多元線性回歸組成的不是直線，是一個多維空間中的超平面，數據點散落在超平面的兩側。

?????????線性關系?

為什么會這樣的關系呢？原因是什么？如果是?線性關系，那么回歸?程可以理解為

?4.最小二乘法

????????線性回歸模型經常用最小二乘逼近來擬合，但他們也可能用別的方法來擬合，比如用最小化“擬合缺陷”在一些其他規范里（比如最小絕對誤差回歸），或者在橋回歸中最小化最小二乘損失函數的懲罰.相反,最小二乘逼近可以用來擬合那些非線性的模型.因此，盡管“最小二乘法”和“線性模型”是緊密相連的，但他們是不能劃等號的。

????????要使損失函數最小，可以將損失函數當作多元函數來處理，采用多元函數求偏導的方法來計算函數的極小值。

對于上面提到的：預測值與真實值之間的誤差

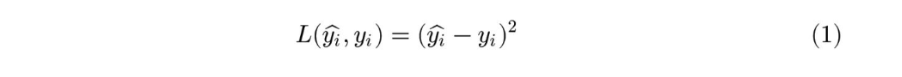
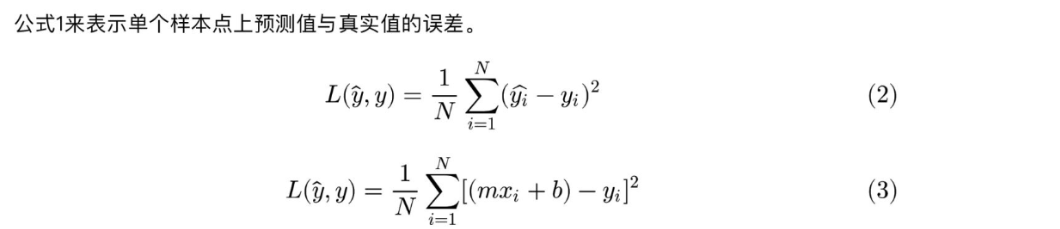
?2.線性回歸項目案例

1.簡單線性回歸分析廣告投入與銷售額關系

導入必要的庫

import pandas as pd
import matplotlib.pyplot as plt  
from sklearn.linear_model import LinearRegression

加載數據

data = pd.read_csv("data(1).csv")

廣告投入	銷售額
29	77
28	62
34	93
31	84
25	59
29	64
32	80
31	75
24	58
33	91
25	51
31	73
26	65
30	84

?數據預處理與可視化?

plt.scatter(data['廣告投入'], data['銷售額'])
plt.xlabel('廣告投入')
plt.ylabel('銷售額')
plt.show()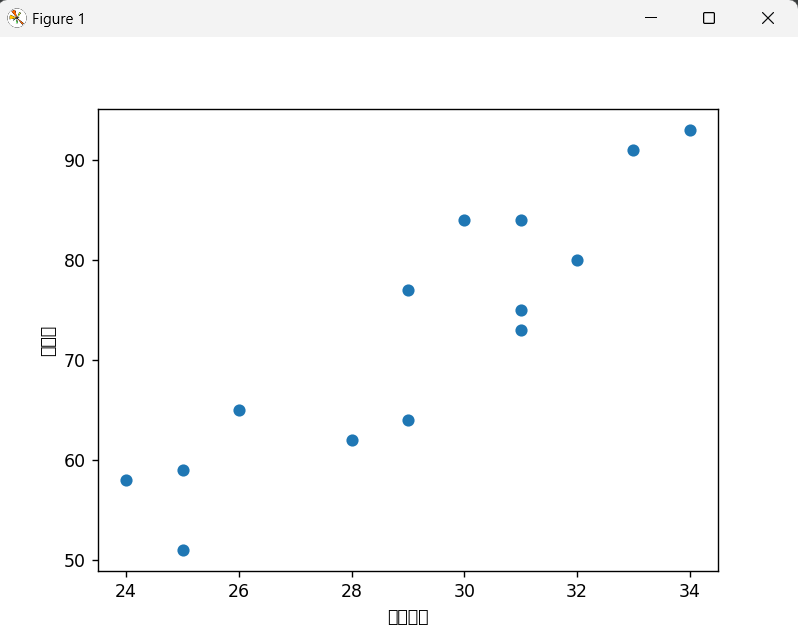

準備訓練數據

x = data[["廣告投入"]]  # 特征矩陣（自變量），需使用二維數組格式
y = data[['銷售額']]   # 目標向量（因變量）

x：選取廣告投入列作為特征
y：選取銷售額列作為目標變量

創建并訓練模型?

estimator = LinearRegression(fit_intercept=True)  # 創建線性回歸模型，包含截距項
estimator.fit(x, y)  # 訓練模型

fit_intercept=True：指定模型包含截距項（即公式中的 b）
fit()方法通過最小二乘法計算最佳擬合參數

輸出模型參數?

print(estimator.coef_)        # 輸出斜率（權重）
print(estimator.intercept_)   # 輸出截距
print("線性回歸模型為: y = {}x + {}".format(estimator.coef_[0][0], estimator.intercept_[0]))

coef_：模型的斜率（即廣告投入對銷售額的影響系數）
intercept_：模型的截距
模型公式：銷售額 = 系數 × 廣告投入 + 截距

評估模型?

score = estimator.score(x, y)  # 計算R2得分
print(score)

score()方法返回模型的 R2（決定系數）
R2 表示模型對數據的擬合程度，取值范圍 [0,1]，越接近 1 表示擬合效果越好

運行結果

[[3.73788546]]
[-36.36123348]
線性回歸模型為: y = [[3.73788546]]x+[-36.36123348]
0.8225092881166945

完整代碼?

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegressiondata=pd.read_csv("data(1).csv")plt.scatter(data['廣告投入'], data['銷售額'])
plt.xlabel('廣告投入')
plt.ylabel('銷售額')
plt.show()x=data[["廣告投入"]]
y=data[['銷售額']]estimator=LinearRegression(fit_intercept=True)estimator.fit(x,y)
print(estimator.coef_)
print(estimator.intercept_)
print("線性回歸模型為: y = {}x+{}".format(estimator.coef_,estimator.intercept_))
score=estimator.score(x,y)
print(score)

2.多元線性回歸分析體重、年齡與收縮壓關系

導入必要的庫導入數據?

import pandas as pd
from sklearn.linear_model import LinearRegression
data = pd.read_csv("多元線性回歸.csv", encoding='gbk', engine='python')

計算相關系數矩陣

corr = data[["體重", "年齡", "血壓收縮"]].corr()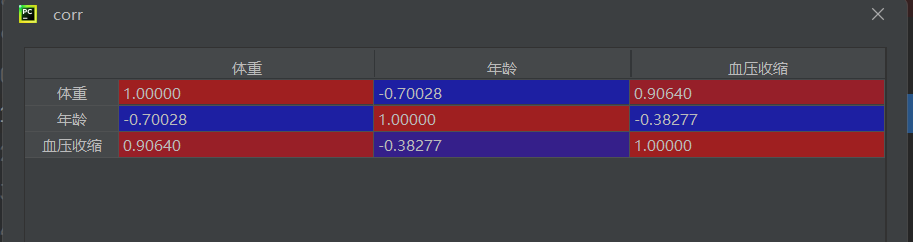

相關系數矩陣可幫助判斷變量間的線性相關程度，絕對值越接近1表示越相關

?準備訓練數據

x = data[['體重', '年齡']]  # 特征矩陣（自變量）
y = data[['血壓收縮']]     # 目標向量（因變量）

x：選取體重和年齡作為特征
y：選取血壓收縮作為目標變量

創建并訓練模型?

lr_model = LinearRegression()
lr_model.fit(x, y)  # 訓練模型

創建線性回歸模型實例
fit()方法通過最小二乘法計算最佳擬合參數

模型評估?

score = lr_model.score(x, y)  # 計算R2得分

score()方法返回模型的 R2（決定系數）
R2 表示模型對數據的擬合程度，取值范圍 [0,1]

預測新數據?

print(lr_model.predict([[80, 60]]))  # 預測體重80kg、年齡60歲的收縮壓
print(lr_model.predict([[70, 30], [70, 20]]))  # 批量預測

predict()方法根據訓練好的模型進行預測
輸入需為二維數組，每行代表一個樣本

輸出模型參數

a = lr_model.coef_       # 獲取系數
b = lr_model.intercept_  # 獲取截距
print("線性回歸模型為: y = {:.2f}x1 + {:.2f}x2 + {:.2f}.".format(a[0][0], a[0][1], b[0]))

運行結果

[[131.97426124]]
[[98.60219521][94.60003367]]
線性回歸模型為: y = 2.14x1 + 0.40x2 + -62.96.

完整代碼

import pandas as pd
from sklearn.linear_model import LinearRegression# 導入數據
data = pd.read_csv("多元線性回歸.csv", encoding='gbk', engine='python')# 打印相關系數矩陣
corr = data[["體重", "年齡", "血壓收縮"]].corr()# 第二步，估計模型參數，建立回歸模型
lr_model = LinearRegression()
x = data[['體重', '年齡']]
y = data[['血壓收縮']]lr_model.fit(x, y)  # 訓練模型# 第四步，對回歸模型進行檢驗
score = lr_model.score(x, y)  # sklearn statsmodes（數理統計這個專業）# 第五步，利用回歸模型進行預測
print(lr_model.predict([[80, 60]]))
print(lr_model.predict([[70, 30], [70, 20]]))"""
a:自變量系數
b:截距
"""
a = lr_model.coef_
b = lr_model.intercept_
print("線性回歸模型為: y = {:.2f}x1 + {:.2f}x2 + {:.2f}.".format(a[0][0], a[0][1], b[0]))
# 線性回歸模型為: y = 2.14x1 + 0.40x2 + -62.96.