一、Oracle數據庫安裝
1.找到軟件的位置 D:\學習軟件\Oracle,并解壓軟件
2.雙擊setup.exe
3.選擇 是
4.去掉勾,下一步
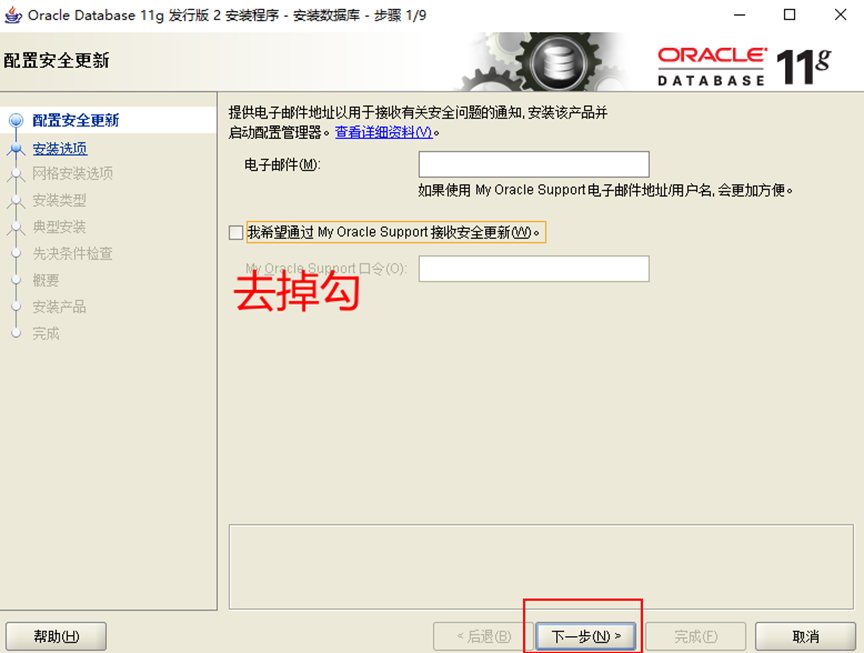
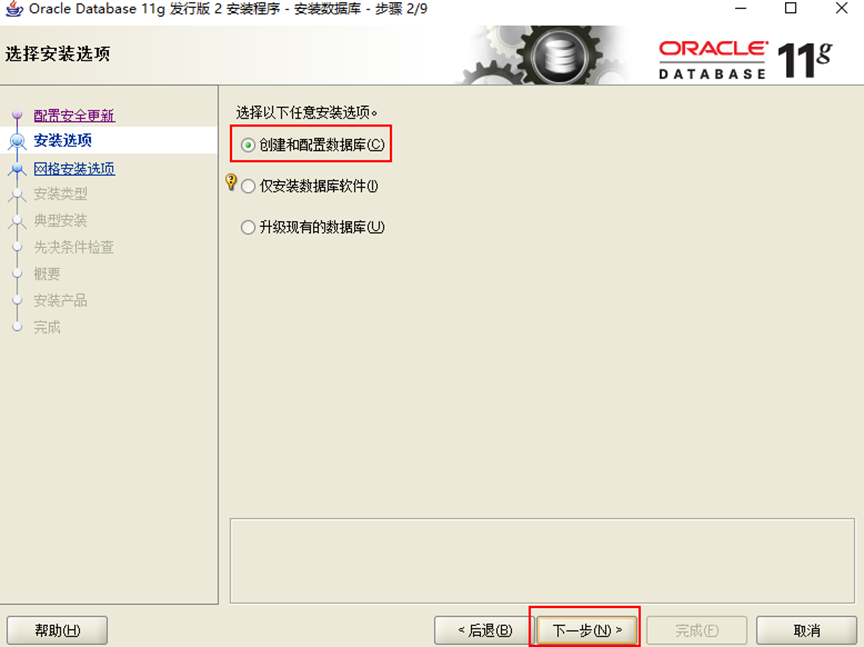
5.創建和配置數據庫,下一步
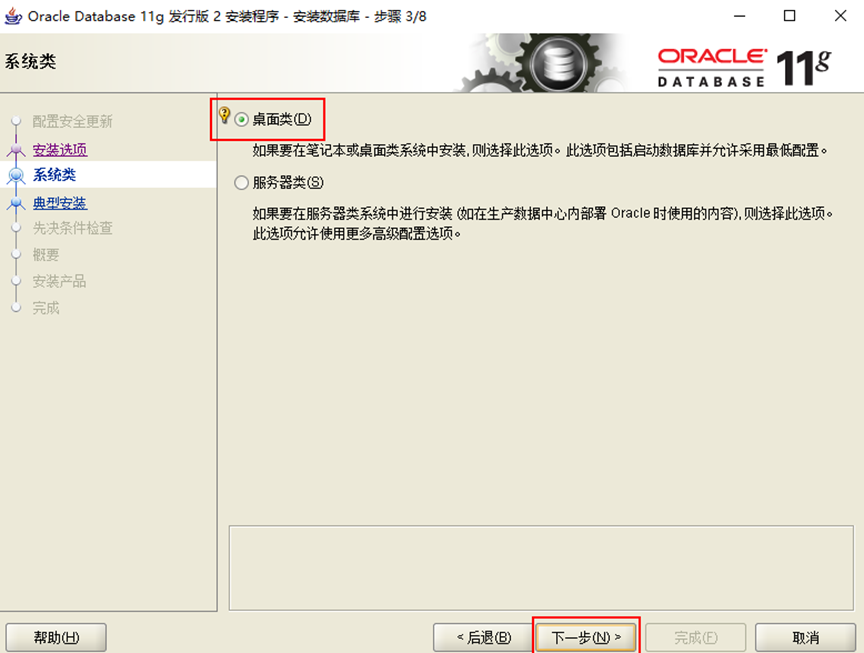
6.桌面類,下一步
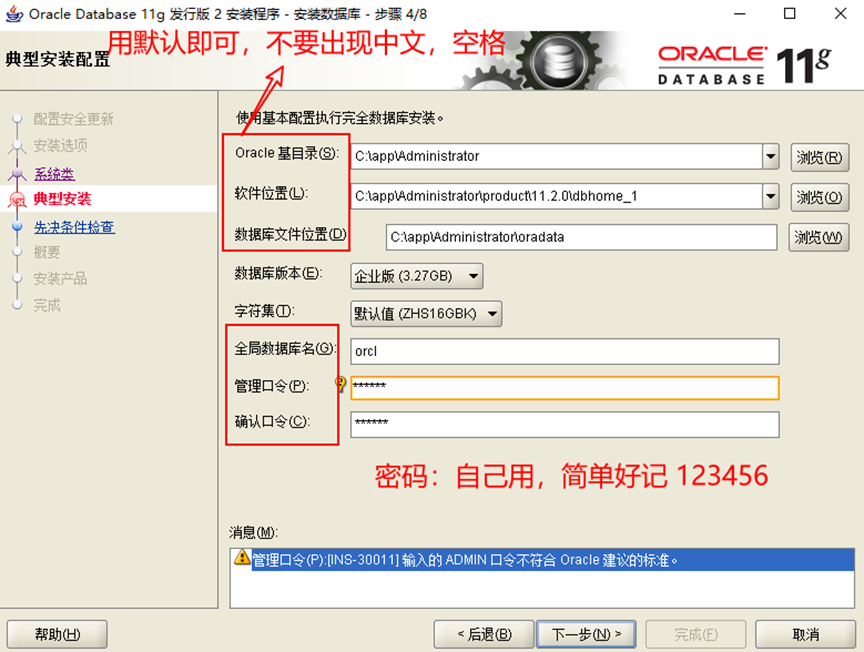
7.配置安裝路徑地址和密碼
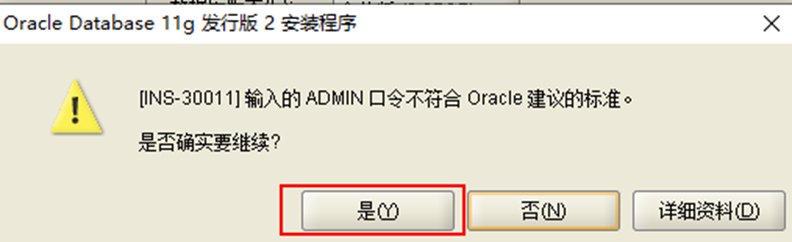
8.點完成
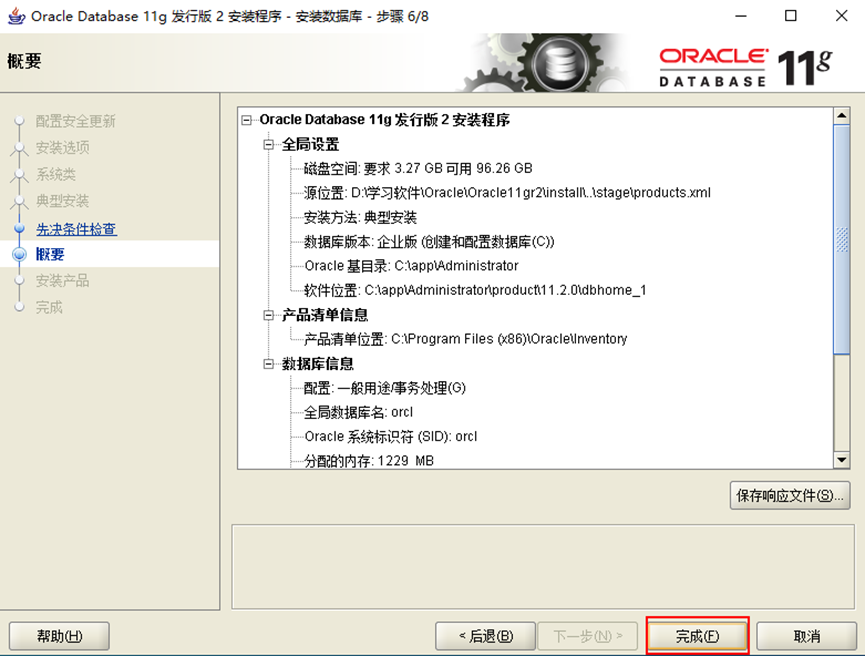
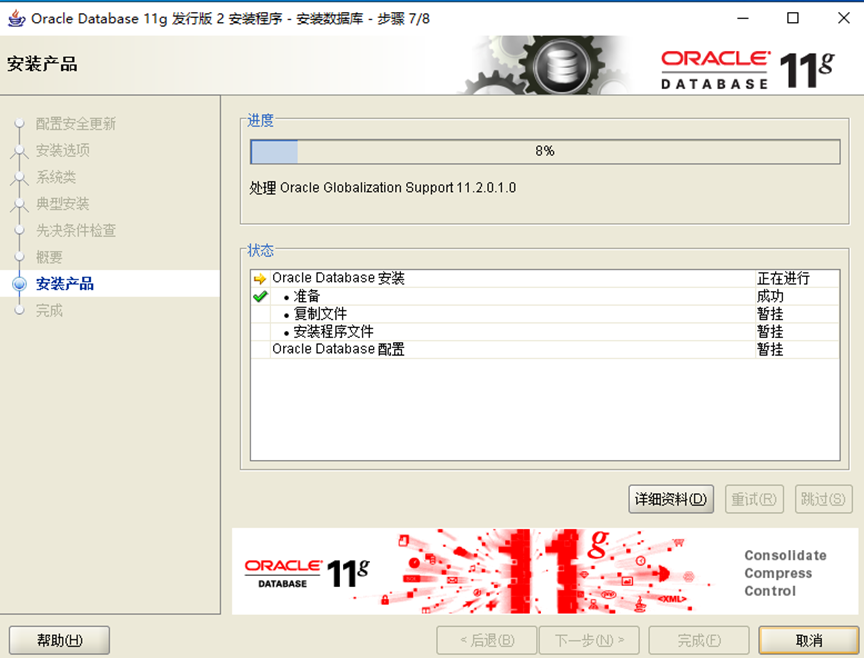
9.正在安裝,稍等片刻
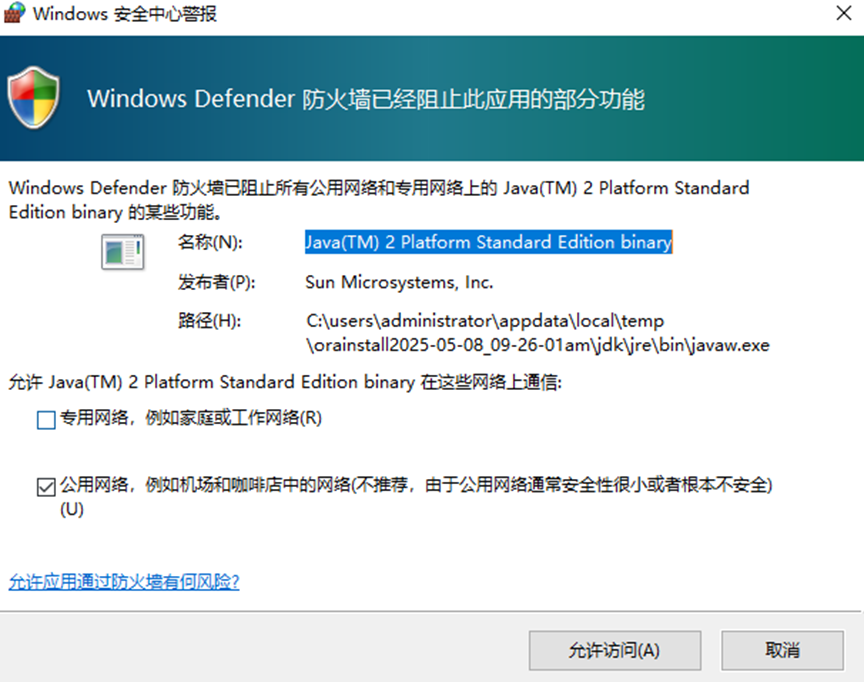
10.有可能會彈出防火墻,允許即可
11.會彈出下面的界面,不要去停止它,讓它慢慢安裝
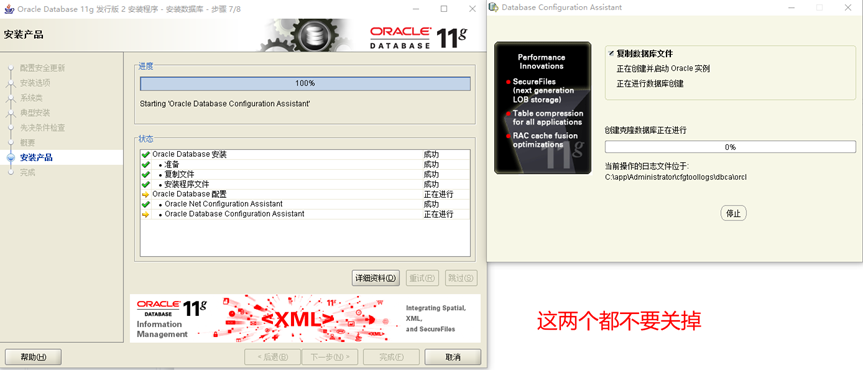
12.裝好之后,會彈出下面的界面,選擇口令管理

13.給scott賬戶設置密碼
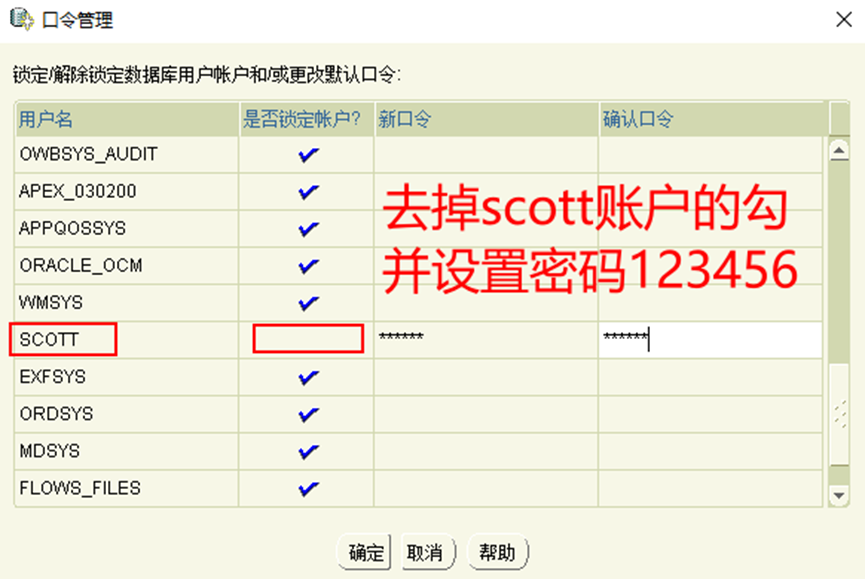
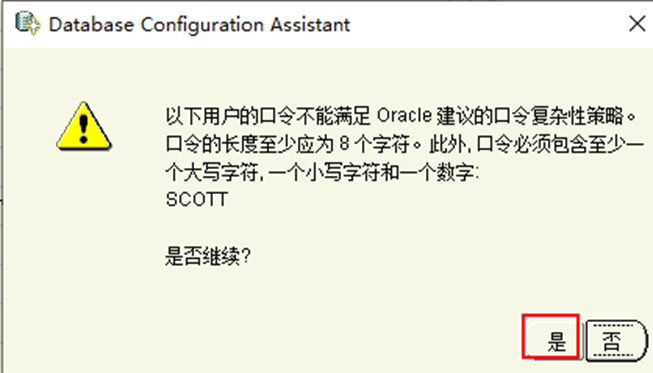
二、plsql客戶端工具安裝
1.找到軟件目錄,并解壓出來
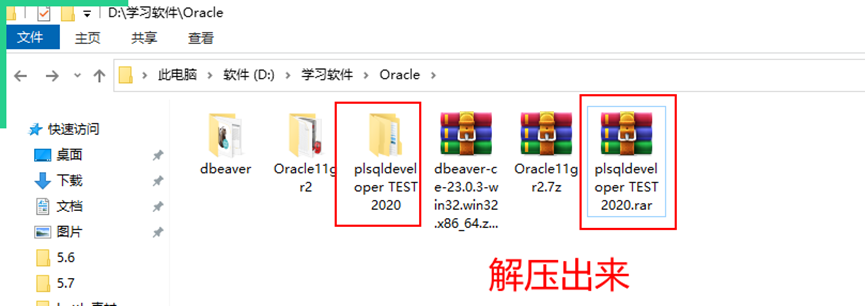
2.雙擊安裝
3.點確定
4.點i agree
5.下一步
6.點下一步,點完成
7.點關閉
8.安裝好之后,就會客戶端工具的圖標
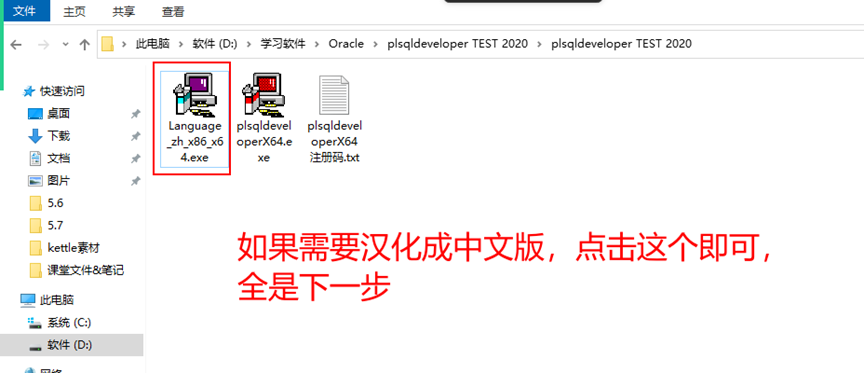
9.如果需要漢化成中文版,可以雙擊下面的,這一步可選
10.雙擊桌面的客戶端圖標
11.登入scott用戶
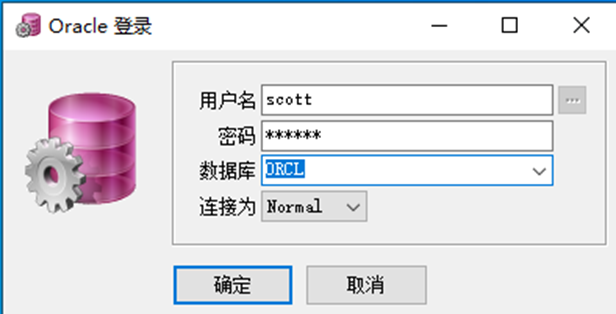
12.左上角顯示scott就代表登入成功
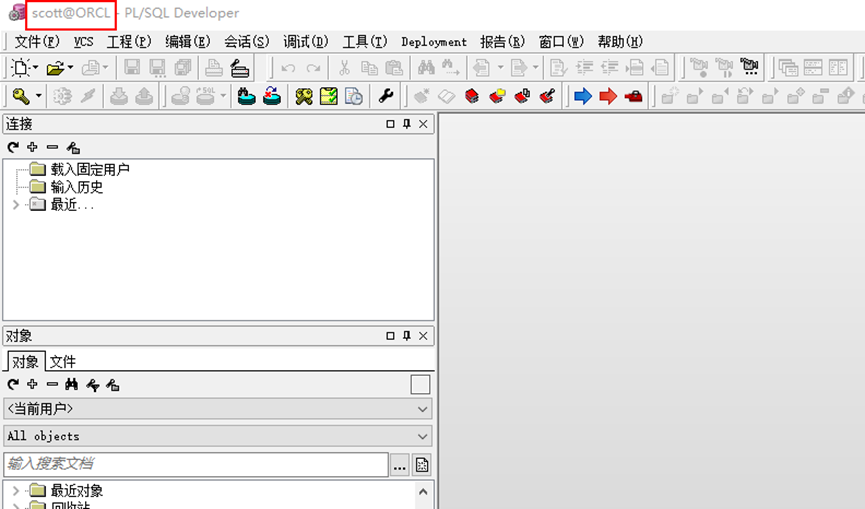
13.點幫助,注冊
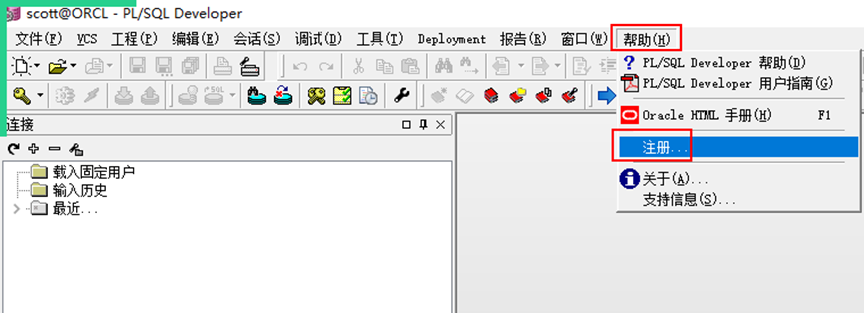
14.注冊
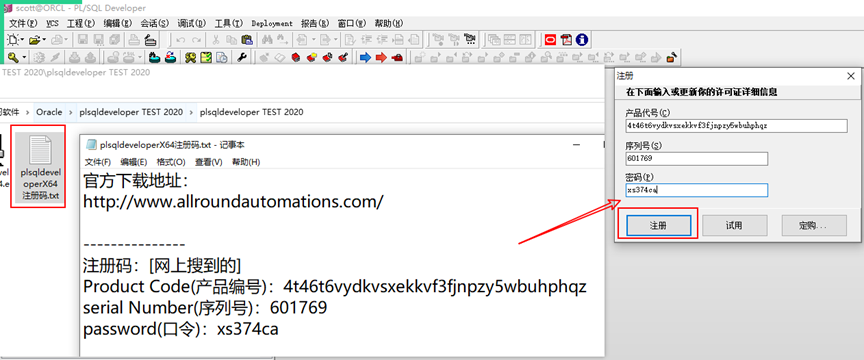



)
實現方案)


![[明道云]-基礎教學2-工作表字段 vs 控件:選哪種?](http://pic.xiahunao.cn/[明道云]-基礎教學2-工作表字段 vs 控件:選哪種?)










)
![【GNSS原理】【LAMBDA】Chapter.12 GNSS定位算法——模糊度固定LAMBDA算法[2025年7月]](http://pic.xiahunao.cn/【GNSS原理】【LAMBDA】Chapter.12 GNSS定位算法——模糊度固定LAMBDA算法[2025年7月])