前言

是看了這個大佬的視頻后想進行一下自己的整理（流程只到了扁平化），如果有問題希望各位大佬能夠給予指正。卷積神經網絡（CNN）到底卷了啥？8分鐘帶你快速了解！_嗶哩嗶哩_bilibilihttps://www.bilibili.com/video/BV1MsrmY4Edi/?spm_id_from=333.1007.top_right_bar_window_history.content.click&vd_source=7c3bfbf39d037fe80c97234396acc524

輸入層

由于自己也不知道設置什么矩陣，就干脆讓deepseek生成0~9的矩陣，每次隨機使用一個數字來進行測試。

• 從預定義的digit_templates中隨機選擇一個數字（0-9）

• 將數字的6x6二進制矩陣轉換為NumPy數組
  關鍵變量：

• digit: 原始數字矩陣（6x6），值為0（黑）或1（白）

# 數字模板（6x6矩陣）
digit_templates = {0: [[0, 1, 1, 1, 1, 0],[1, 0, 0, 0, 0, 1],[1, 0, 0, 0, 0, 1],[1, 0, 0, 0, 0, 1],[1, 0, 0, 0, 0, 1],[0, 1, 1, 1, 1, 0]],1: [[0, 0, 1, 1, 0, 0],[0, 1, 1, 1, 0, 0],[0, 0, 1, 1, 0, 0],[0, 0, 1, 1, 0, 0],[0, 0, 1, 1, 0, 0],[0, 1, 1, 1, 1, 0]],2: [[0, 1, 1, 1, 1, 0],[1, 0, 0, 0, 0, 1],[0, 0, 0, 1, 1, 0],[0, 1, 1, 0, 0, 0],[1, 0, 0, 0, 0, 0],[1, 1, 1, 1, 1, 1]],3: [[1, 1, 1, 1, 1, 0],[0, 0, 0, 0, 0, 1],[0, 1, 1, 1, 1, 0],[0, 0, 0, 0, 0, 1],[0, 0, 0, 0, 0, 1],[1, 1, 1, 1, 1, 0]],4: [[1, 0, 0, 0, 1, 0],[1, 0, 0, 0, 1, 0],[1, 0, 0, 0, 1, 0],[1, 1, 1, 1, 1, 1],[0, 0, 0, 0, 1, 0],[0, 0, 0, 0, 1, 0]],5: [[1, 1, 1, 1, 1, 1],[1, 0, 0, 0, 0, 0],[1, 1, 1, 1, 1, 0],[0, 0, 0, 0, 0, 1],[0, 0, 0, 0, 0, 1],[1, 1, 1, 1, 1, 0]],6: [[0, 1, 1, 1, 1, 0],[1, 0, 0, 0, 0, 0],[1, 1, 1, 1, 1, 0],[1, 0, 0, 0, 0, 1],[1, 0, 0, 0, 0, 1],[0, 1, 1, 1, 1, 0]],7: [[1, 1, 1, 1, 1, 1],[0, 0, 0, 0, 1, 0],[0, 0, 0, 1, 0, 0],[0, 0, 1, 0, 0, 0],[0, 1, 0, 0, 0, 0],[1, 0, 0, 0, 0, 0]],8: [[0, 1, 1, 1, 1, 0],[1, 0, 0, 0, 0, 1],[0, 1, 1, 1, 1, 0],[1, 0, 0, 0, 0, 1],[1, 0, 0, 0, 0, 1],[0, 1, 1, 1, 1, 0]],9: [[0, 1, 1, 1, 1, 0],[1, 0, 0, 0, 0, 1],[1, 0, 0, 0, 0, 1],[0, 1, 1, 1, 1, 1],[0, 0, 0, 0, 0, 1],[0, 1, 1, 1, 1, 0]]
}# 隨機選擇數字
random_digit = randint(0, 9)
digit = np.array(digit_templates[random_digit])

Padding

將6*6的矩陣邊界填充0擴展為8x8矩陣，防止丟失邊緣信息。

numpy.pad()函數詳解_numpy pad-CSDN博客https://blog.csdn.net/weixin_41862755/article/details/128336141

• 在原始矩陣周圍添加一圈0（pad_width=1）

• 將6x6矩陣擴展為8x8，防止卷積時邊緣信息丟失
  輸出：

• padded: 填充后的矩陣（8x8）

padded = np.pad(digit, pad_width=1, mode='constant')  # 邊界填充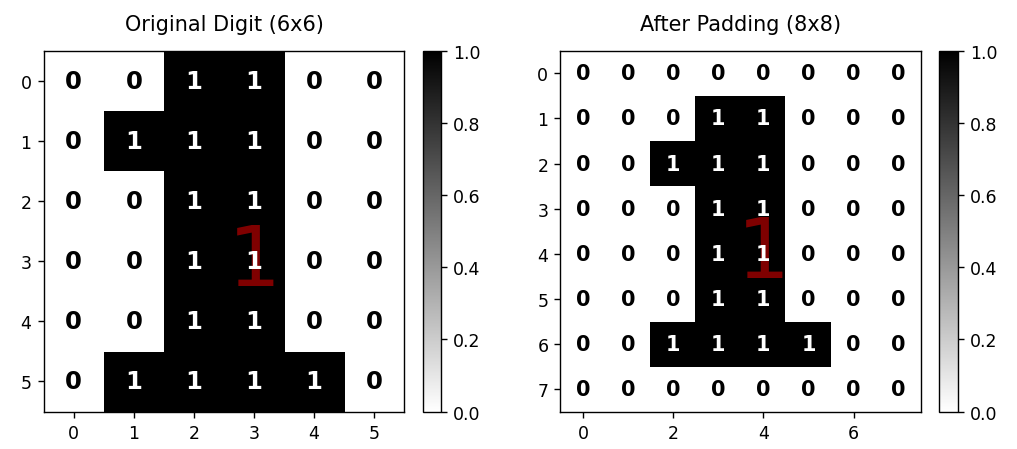

卷積

局部加權求和（對應相乘再相加），提取輸入數據的局部特征，形成特征映射。

• conv2d函數實現滑動窗口卷積運算

• 使用垂直核（kernel_v）檢測垂直邊緣特征

• 使用水平核（kernel_h）檢測水平邊緣特征
  關鍵參數：

• kernel_v:?[[0,1,0], [0,1,0], [0,1,0]]（強化垂直線條）

• kernel_h:?[[0,0,0], [1,1,1], [0,0,0]]（強化水平線條）
  輸出：

• conv_v: 垂直卷積結果（6x6矩陣）

• conv_h: 水平卷積結果（6x6矩陣）

# 定義卷積核
kernel_v = np.array([[0, 1, 0], [0, 1, 0], [0, 1, 0]])  # 垂直特征
kernel_h = np.array([[0, 0, 0], [1, 1, 1], [0, 0, 0]])  # 水平特征def conv2d(image, kernel):# 手動實現卷積運算h, w = image.shapek_h, k_w = kernel.shapeoutput = np.zeros((h - k_h + 1, w - k_w + 1))for y in range(h - k_h + 1):for x in range(w - k_w + 1):output[y, x] = np.sum(image[y:y + k_h, x:x + k_w] * kernel)return output.astype(int)conv_v = conv2d(padded, kernel_v)  # 垂直卷積
conv_h = conv2d(padded, kernel_h)  # 水平卷積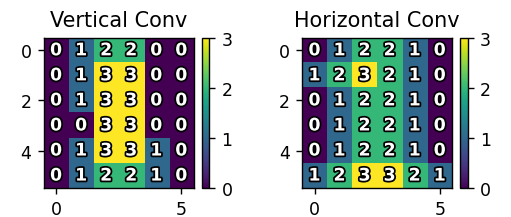

激活

這個視頻中沒有，然后代碼中也沒起作用，因為沒有出現值為負數出現。激活函數可以進行非線性變換，使網絡能夠學習復雜模式，可以進行特征過濾，保留有用特征，抑制噪聲，可以優化訓練，控制梯度流動，提高模型收斂速度。

• 對卷積結果應用ReLU（Rectified Linear Unit）激活函數

• 保留正值，負值置為0（非線性變換）
  輸出：

• relu_v: 垂直特征激活結果（6x6）

• relu_h: 水平特征激活結果（6x6）

relu_v = np.maximum(0, conv_v)  # ReLU激活
relu_h = np.maximum(0, conv_h)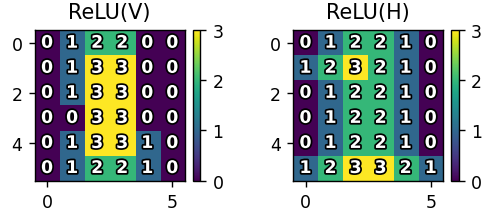

池化

池化能夠進行信息壓縮，用更少的參數表達關鍵特征，可以不變性增強，使模型對輸入的小變化更魯棒，可以計算效率，加速訓練和推理過程。

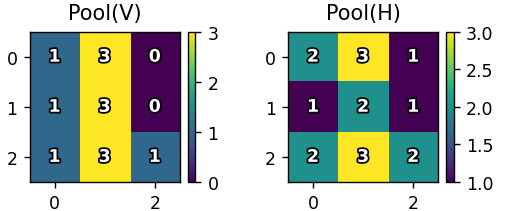
• maxpool2d函數實現2x2最大池化（步長=2）

• 降低特征圖維度，保留顯著特征（保留2*2中的最大值）
  輸出：

• pool_v: 垂直特征池化結果（3x3）

• pool_h: 水平特征池化結果（3x3）

扁平化

扁平化可以結構轉換，讓多維特征轉換成一維向量，可以信息整合，合并不同特征提取路徑的結果，起到橋梁作用，連接特征提取層與分類決策層。

• 將池化后的3x3矩陣展平為一維向量（flatten()）

• 合并垂直和水平特征向量（最終18維向量）
  輸出：

• flattened: 合并后的特征向量（形狀：(18,)）

flattened = np.concatenate([pool_v.flatten(), pool_h.flatten()])

可視化

• 使用Matplotlib繪制處理流程各階段的結果

• 關鍵可視化內容：

  • 原始數字矩陣（標注0/1值）

  • 卷積/激活/池化結果（熱力圖+數值標注）

  • 扁平化向量（條形圖，紅色標記激活特征）

完整代碼

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patheffects as path_effects
from random import randint# 數字模板（6x6矩陣）
digit_templates = {0: [[0, 1, 1, 1, 1, 0],[1, 0, 0, 0, 0, 1],[1, 0, 0, 0, 0, 1],[1, 0, 0, 0, 0, 1],[1, 0, 0, 0, 0, 1],[0, 1, 1, 1, 1, 0]],1: [[0, 0, 1, 1, 0, 0],[0, 1, 1, 1, 0, 0],[0, 0, 1, 1, 0, 0],[0, 0, 1, 1, 0, 0],[0, 0, 1, 1, 0, 0],[0, 1, 1, 1, 1, 0]],2: [[0, 1, 1, 1, 1, 0],[1, 0, 0, 0, 0, 1],[0, 0, 0, 1, 1, 0],[0, 1, 1, 0, 0, 0],[1, 0, 0, 0, 0, 0],[1, 1, 1, 1, 1, 1]],3: [[1, 1, 1, 1, 1, 0],[0, 0, 0, 0, 0, 1],[0, 1, 1, 1, 1, 0],[0, 0, 0, 0, 0, 1],[0, 0, 0, 0, 0, 1],[1, 1, 1, 1, 1, 0]],4: [[1, 0, 0, 0, 1, 0],[1, 0, 0, 0, 1, 0],[1, 0, 0, 0, 1, 0],[1, 1, 1, 1, 1, 1],[0, 0, 0, 0, 1, 0],[0, 0, 0, 0, 1, 0]],5: [[1, 1, 1, 1, 1, 1],[1, 0, 0, 0, 0, 0],[1, 1, 1, 1, 1, 0],[0, 0, 0, 0, 0, 1],[0, 0, 0, 0, 0, 1],[1, 1, 1, 1, 1, 0]],6: [[0, 1, 1, 1, 1, 0],[1, 0, 0, 0, 0, 0],[1, 1, 1, 1, 1, 0],[1, 0, 0, 0, 0, 1],[1, 0, 0, 0, 0, 1],[0, 1, 1, 1, 1, 0]],7: [[1, 1, 1, 1, 1, 1],[0, 0, 0, 0, 1, 0],[0, 0, 0, 1, 0, 0],[0, 0, 1, 0, 0, 0],[0, 1, 0, 0, 0, 0],[1, 0, 0, 0, 0, 0]],8: [[0, 1, 1, 1, 1, 0],[1, 0, 0, 0, 0, 1],[0, 1, 1, 1, 1, 0],[1, 0, 0, 0, 0, 1],[1, 0, 0, 0, 0, 1],[0, 1, 1, 1, 1, 0]],9: [[0, 1, 1, 1, 1, 0],[1, 0, 0, 0, 0, 1],[1, 0, 0, 0, 0, 1],[0, 1, 1, 1, 1, 1],[0, 0, 0, 0, 0, 1],[0, 1, 1, 1, 1, 0]]
}# 隨機選擇數字
random_digit = randint(0, 9)
digit = np.array(digit_templates[random_digit])# 定義卷積核
kernel_v = np.array([[0, 1, 0], [0, 1, 0], [0, 1, 0]])  # 垂直特征
kernel_h = np.array([[0, 0, 0], [1, 1, 1], [0, 0, 0]])  # 水平特征def process_digit(digit):# Paddingpadded = np.pad(digit, pad_width=1, mode='constant')# 卷積計算def conv2d(image, kernel):h, w = image.shapek_h, k_w = kernel.shapeoutput = np.zeros((h - k_h + 1, w - k_w + 1))for y in range(h - k_h + 1):for x in range(w - k_w + 1):output[y, x] = np.sum(image[y:y + k_h, x:x + k_w] * kernel)return output.astype(int)  # 轉換為整型conv_v = conv2d(padded, kernel_v)conv_h = conv2d(padded, kernel_h)# ReLU激活relu_v = np.maximum(0, conv_v).astype(int)  # 轉換為整型relu_h = np.maximum(0, conv_h).astype(int)  # 轉換為整型# 最大池化def maxpool2d(image, size=2):h, w = image.shapereturn np.array([[np.max(image[i:i + size, j:j + size])for j in range(0, w, size)]for i in range(0, h, size)]).astype(int)  # 轉換為整型pool_v = maxpool2d(relu_v)pool_h = maxpool2d(relu_h)# 扁平化flattened = np.concatenate([pool_v.flatten(), pool_h.flatten()]).astype(int)  # 轉換為整型return {'original': digit,'padded': padded,'conv_v': conv_v,'conv_h': conv_h,'relu_v': relu_v,'relu_h': relu_h,'pool_v': pool_v,'pool_h': pool_h,'flattened': flattened}def visualize_flow(results):fig = plt.figure(figsize=(20, 12))plt.suptitle(f'CNN Processing Flow for Digit {random_digit}', fontsize=18, y=0.97)grid = plt.GridSpec(4, 6, hspace=0.4, wspace=0.3)# 創建文本描邊效果text_effect = [path_effects.withStroke(linewidth=2, foreground='black')]# 原始圖像 - 顯示阿拉伯數字ax1 = fig.add_subplot(grid[0:2, 0:2])img1 = ax1.imshow(results['original'], cmap='binary')plt.colorbar(img1, ax=ax1, fraction=0.046, pad=0.04)ax1.set_title("Original Digit (6x6)", pad=12)ax1.text(3, 3, str(random_digit),ha='center', va='center',color='red', fontsize=48, alpha=0.5)for y in range(results['original'].shape[0]):for x in range(results['original'].shape[1]):display_val = '1' if results['original'][y, x] > 0.5 else '0'ax1.text(x, y, display_val,ha='center', va='center',color='white' if results['original'][y, x] > 0.5 else 'black',fontsize=14, weight='bold')# Padding后的圖像 - 顯示阿拉伯數字ax2 = fig.add_subplot(grid[0:2, 2:4])img2 = ax2.imshow(results['padded'], cmap='binary')plt.colorbar(img2, ax=ax2, fraction=0.046, pad=0.04)ax2.set_title("After Padding (8x8)", pad=12)ax2.text(4, 4, str(random_digit),ha='center', va='center',color='red', fontsize=48, alpha=0.5)for y in range(results['padded'].shape[0]):for x in range(results['padded'].shape[1]):display_val = '1' if results['padded'][y, x] > 0.5 else '0'ax2.text(x, y, display_val,ha='center', va='center',color='white' if results['padded'][y, x] > 0.5 else 'black',fontsize=12, weight='bold')# 右側圖像的統一設置right_plots = {'conv_v': ('Vertical Conv', grid[0, 4]),'conv_h': ('Horizontal Conv', grid[0, 5]),'relu_v': ('ReLU(V)', grid[1, 4]),'relu_h': ('ReLU(H)', grid[1, 5]),'pool_v': ('Pool(V)', grid[2, 4]),'pool_h': ('Pool(H)', grid[2, 5])}for key, (title, pos) in right_plots.items():ax = fig.add_subplot(pos)img = ax.imshow(results[key], cmap='viridis')plt.colorbar(img, ax=ax, fraction=0.046, pad=0.04)ax.set_title(title, pad=7)for y in range(results[key].shape[0]):for x in range(results[key].shape[1]):ax.text(x, y, f"{results[key][y, x]:d}",  # 使用整型格式ha='center', va='center',color='white',fontsize=10, weight='bold',path_effects=text_effect)# 扁平化ax9 = fig.add_subplot(grid[3, :])bars = ax9.bar(range(len(results['flattened'])), results['flattened'])for j, val in enumerate(results['flattened']):if val > 0:bars[j].set_color('red')ax9.text(j, val / 2, f"{val:d}",  # 使用整型格式ha='center', va='center',color='white',weight='bold',path_effects=text_effect)ax9.set_xticks(range(len(results['flattened'])))ax9.set_title("Flattened Vector (Red = Activated Features)", pad=12)plt.tight_layout()plt.show()# 執行流程
results = process_digit(digit)
print(f"Processing digit: {random_digit}")
print("Flattened vector:", results['flattened'])
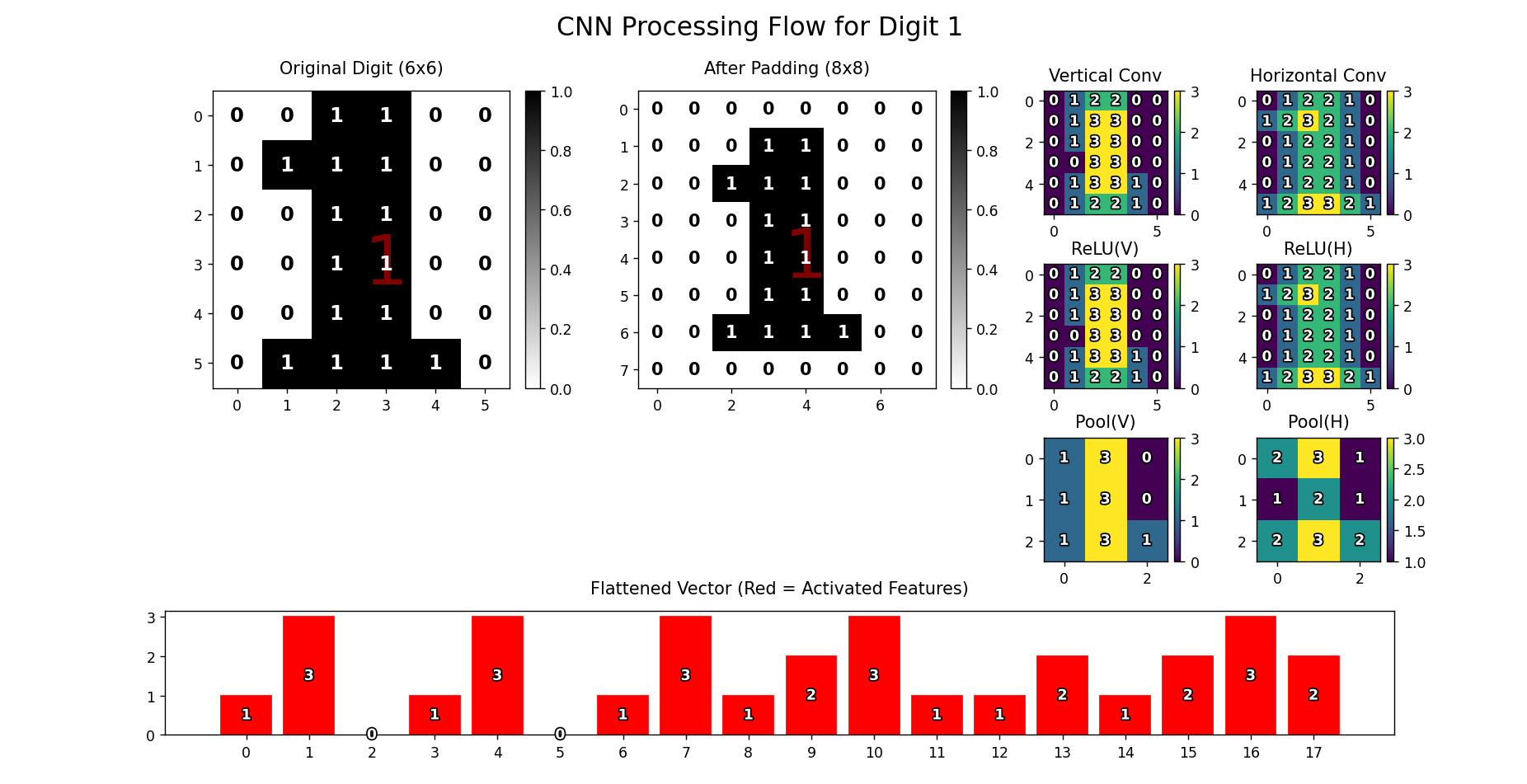
visualize_flow(results)

Processing digit: 1
Flattened vector: [1 3 0 1 3 0 1 3 1 2 3 1 1 2 1 2 3 2]?

?