暑期算法訓練.9

43 .力扣75 顏色分類

43.1 題目解析：

43.2 算法思路：

43.3 代碼演示：

43.4 總結反思：

44. 力扣 912 排序數組

44.1 題目解析：

44.2 算法思路：

44.3 代碼演示：

?編輯

44.4 總結反思：

45. 力扣215 數組中第k個最大的元素

45.1 題目解析：

45.2 算法思路：

?編輯?

45.3 代碼演示：

45.4 總結反思

?46. 劍指offer 40.最小的k

46.1 題目解析：

?46.2 算法思路：

46.3 代碼演示：

?編輯

46.4 總結反思

43 .力扣75 顏色分類

43.1 題目解析：

咱們今天講的題目都是涉及到一個算法，就是分治算法，即分而治之。顧名思義，就是把一個大問題分成很多個小問題，一直分，直到那個小問題可以被解決為止。之后再回溯，這個時候，那個大問題，也基本就被解決了.......以此類推即可

這道題目很好理解，就是排序，但是不可以使用sort函數，所以就增加了一點難度。

43.2 算法思路：

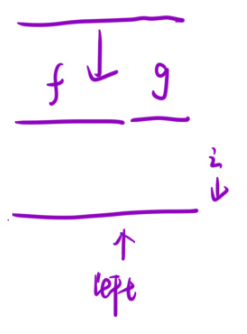
本題咱們可以使用三指針來做。那么咱們之前學過雙指針對吧。

遍歷i，從左往右進行遍歷，之后判斷left，最終left要停在結束的位置即可。把整個數組分成了2份。

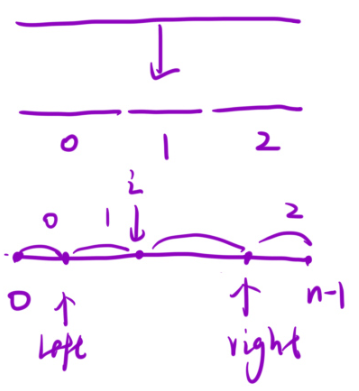
好，那么類比一下，咱們可以推出三指針：

其實最后是把整個數組分成了四部分：

i：遍歷數組

left：標記0區域的最右側

right：標記2區域的最左側

那么[0,left]才全為0，那么得從left+1開始才是1的區域（因為在數組中，是一個一個的數。因為這個數在0區間內，那么下一個數只能在1區間內）直到i-1。（因為i這個位置還沒有掃描呢，還沒有判斷，所以說，只可以到i-1）。之后i到right-1為掃描元素，后面的[right,n-1]才全都是2.

之所以這么算，是因為：

left與right都是從數組之外開始的。

那么，咱們先來看總結的規律：

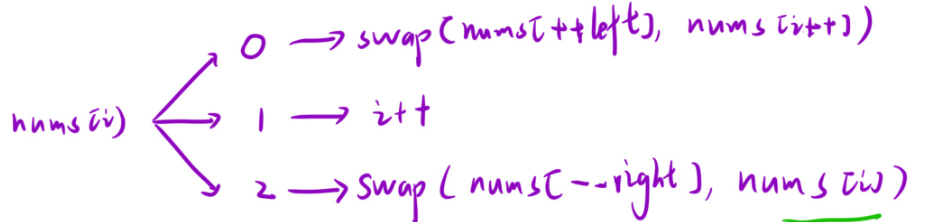1.nums[i]：為0的時候，0應該是在left這個區間內的，得讓nums[i]與nums[left+1]交換，為什么與left+1?交換呢？因為咱們的left，right這倆個指針也得動啊，那你0換到left+1，left再加加，不就正好[0,left]為0了嘛？之后i再加加，因為此時[left+1,i-1]，此時i++完了，那么i-1才是剛才交換后1的位置（i從左往右挪動到這的時候，差不多可以這么挪動了，之前left+1這個位置，差不多是1，就算不是也沒事）。那么若1正好在left+1的地方，i正好為0.也要交換（自己交換自己）。交換之后兩個都要加加。此時swap([nums[++left],nums[i++]),既然都要寫left+1交換，且后面left還要加加，不如直接寫++left。

2.當nums[i]恰好為1的時候，直接i++即可。因為i-1的位置得為1.

3.若nums[i]為2，那么swap(nums[--right],nums[i])，因為right的位置為2，且right后面還得減減，所以得讓right-1位置與i交換，之后right--。但是沒交換之前right-1位置為未掃描，交換后i位置還是未掃描，所以i不用移動！

且直到循環到i==right的時候，因為此時待掃描的區間已經沒有了。循環也就停止了。即while(i<right)

好了，本題的算法終于分析完了。本題的算法對于后面的題目也有用處，所以大家要好好的研讀一下。

43.3 代碼演示：

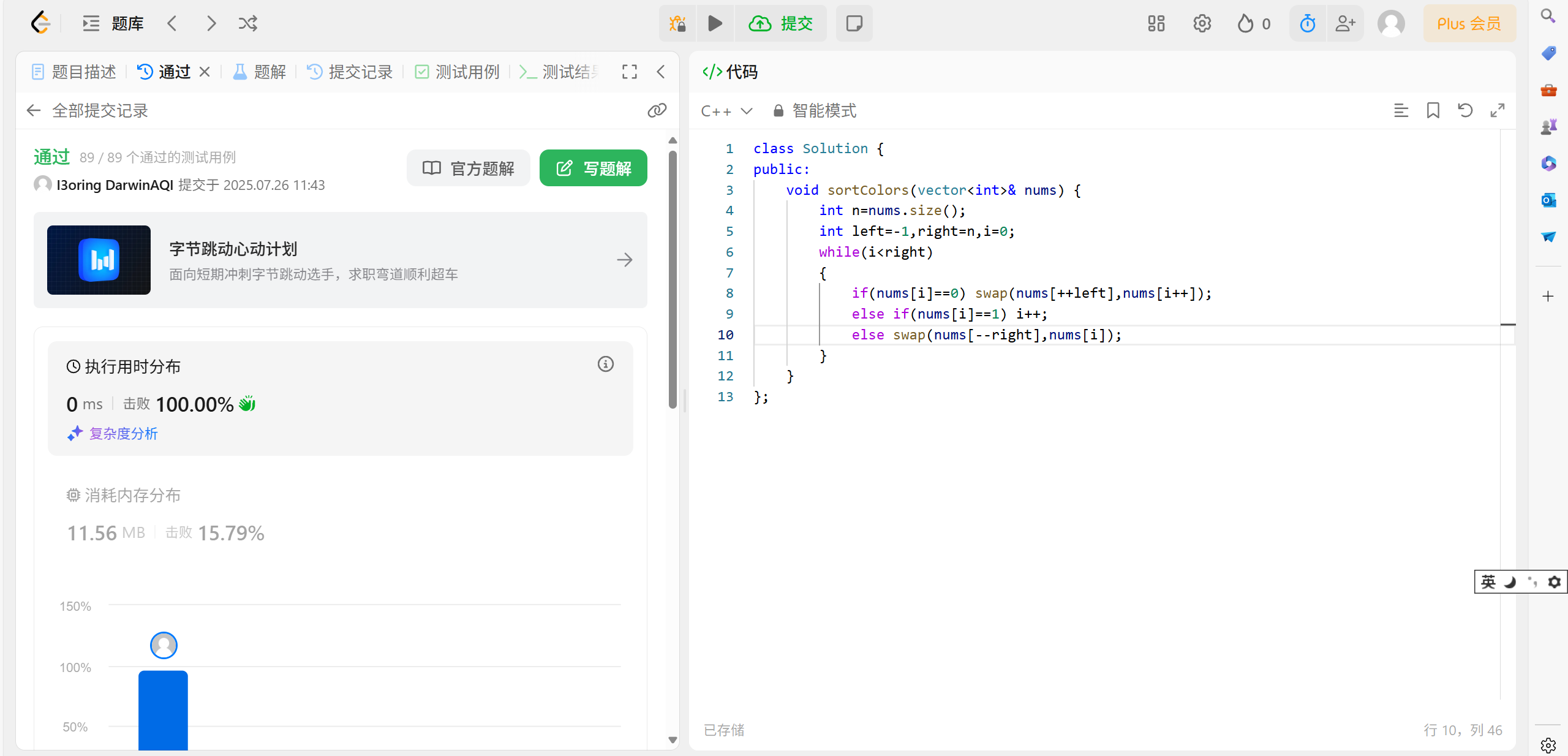
void sortColors(vector<int>& nums) {int n = nums.size();int left = -1, right = n, i = 0;while (i < right){if (nums[i] == 0) swap(nums[++left], nums[i++]);else if (nums[i] == 1) i++;else swap(nums[--right], nums[i]);}
}
int main()
{vector<int> nums = { 2,0,1,0,2,1 };sortColors(nums);for (auto& e : nums){cout << e << "";}cout << endl;return 0;
}

43.4 總結反思：

代碼量其實還是挺少的，只要還是看這個思路一定要掌握。

44. 力扣 912 排序數組

44.1 題目解析：

題目很好理解，就是讓你排序。

44.2 算法思路：

咱們這道題目采用的是快速排序，那么之前咱們一定學過將數組分成兩份的那種快速排序。那種也可以解決這種問題。

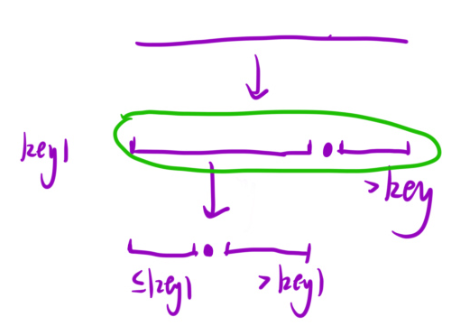但是呢，當所有的元素有一樣的時候，這個時候，這個key就會跑到最右側。那么下次分的時候，還是分這個一大塊。所以時間復雜度就是O（n^2)，挺不好。

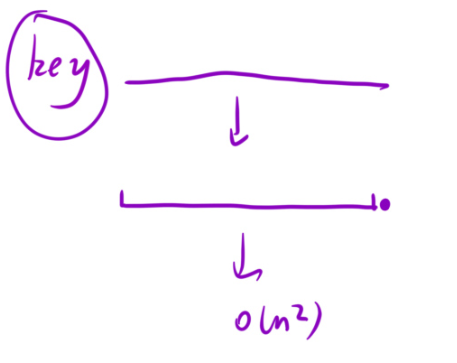所以，咱們今天將使用數組分三塊來實現快速排序（key將數組分成了三塊）

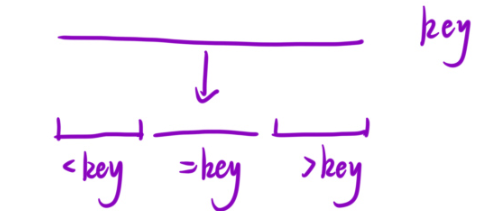最后等于key的這個部分就不需要再管了，只需要對小于key的，以及大于key的再進行遞歸就可以了。

最后還是

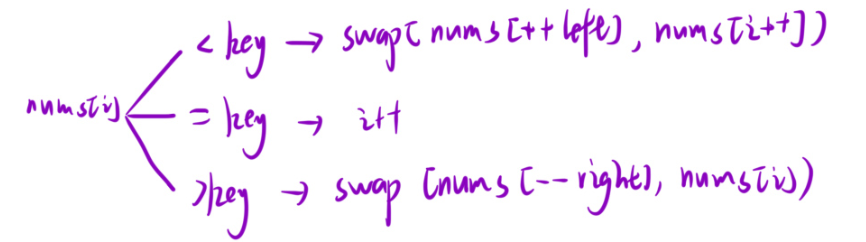還是這些，所以搞懂上一題的算法很有必要。

那么為什么說數組分三塊的效率更高呢？因為當元素都一樣的時候，由于咱們只需要對小于key以及大于key的進行遞歸，但是元素都一樣了，根本不需要遞歸了。所以分一次就可以停止了。時間復雜度就是O（n）,肯定快。

2.優化：使用隨機的方式選擇基準值

快排時復雜度要想靠近N*logN,必須得使用隨機方式選基準值，因為只有這種方式才是等概率的。證明方法大家可以去《算法導論》這本書上找。

注意，上面的，這個left+r%(right-left+1)僅僅只是下標，咱們還得在外面套上nums才可以。

別忘了還得種下一個隨機數種子：srand(time(NULL))

44.3 代碼演示：

// 先聲明 Random 和 qsortl。因為程序是從上到下執行的，所以說你要是不提前聲明存在這兩個函數的話，編譯器是找不到的，當然，你在做力扣的題目的時候，是不需要寫的
int Random(vector<int>& nums, int left, int right);
void qsortl(vector<int>& nums, int l, int r);vector<int> sortArray(vector<int>& nums) {srand(time(NULL));//種下一顆隨機數種子qsortl(nums, 0, nums.size() - 1);//這個其實就是給后面要實現的qsort函數進行傳參return nums;}void qsortl(vector<int>& nums, int l, int r)//這個是區間的左端點與區間的右段點，這個l其實就是0，r就是nums.size()-1（這個只是最初始的是0跟nums.size()-1，后面的就跟遞歸有關了{if (l >= r) return;//說明此時只有一個元素，或者是區間不存在，直接返回即可int key = Random(nums, l, r);int i = l, left = l - 1, right = r + 1;//這個地方涉及到遞歸，所以i是遍歷的l到r，但是遞歸的時候，l與r不是每次都是一樣的數值，所以，i得賦值為l(這個不是數字1)while (i < right){if (nums[i] < key) swap(nums[++left], nums[i++]);else if (nums[i] == key) i++;else swap(nums[--right], nums[i]);}//遞歸//[l,left][left+1,right-1][right,r]qsortl(nums, l, left);qsortl(nums, right, r);}int Random(vector<int>& nums, int left, int right)//這個時候才是對第一次定義的qsort中的left，right的應用{int r = rand();return nums[r % (right - left + 1) + left];}int main()
{vector<int> nums = { 5,2,3,1 };vector<int> outcome = sortArray(nums);for (auto& e : outcome){cout << e << "";}cout << endl;return 0;
}

這道題目開始，i就是l（不是1），不是0了。因為i的作用就是遍歷區間，雖然說第一次的區間是0到n-1，但是還有遞歸啊，遞歸后的這個i就不能再是0了。所以直接讓i隨著l變化就可以了?

代碼確實挺長的，但是大家只要理解了思路，就挺簡單的。

44.4 總結反思：

其實這道題目還是運用了數組分三塊加上隨機產生基準值。大家以后寫快速排序的時候，也可以這么寫，這么寫是比數組分兩塊來進行寫，寫的快的。

45. 力扣215 數組中第k個最大的元素

45.1 題目解析：

本題就是典型的topk問題，topk問題的問法有很多，比如1.找第k大? 2.找第k小? ?3.前k大? 4.前k小

通常可以使用堆排序（時復為O（n*logn）），以及今天介紹的快速選擇算法：（時復為O（n））。這里的快速選擇算法，只需要去一個區間尋找就可以了。

45.2 算法思路：

?

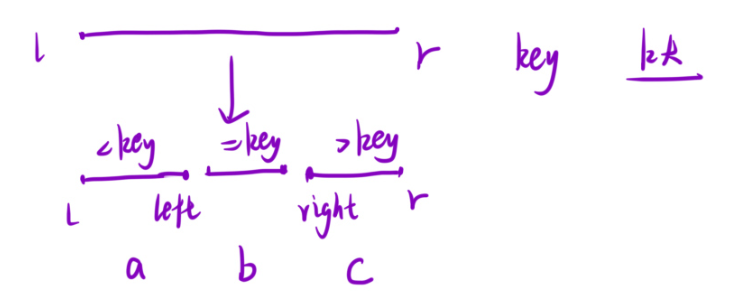a，b，c代表的是區間的元素的個數。

那么1.若c>=k,則第k個大的元素會落在[right,r]這個區間內，去這兒找第k個大的元素（后面還得繼續在這個區間內qsort，代碼中有的，記得看代碼）?

2.第二種情況，說明第一種情況一定不成立：b+c>=k,因為c>=k不成立（c<k),所以第k大個元素，一定在b這個區間內，則直接返回key。

3.則第一種與第二種情況一定不成立。所以去[l,left]內尋找，不就是找第k-b-c個大的元素嘛？

所以快速選擇就是根據數量劃分去某一個區間找。

這里需要算一個區間的長度：咱們直到左閉右閉的區間長度是right-left+1，所以c的區間長度是r-right+1.但是b的區間長度right-1-（left+1）+1，就是right-left-1.

45.3 代碼演示：

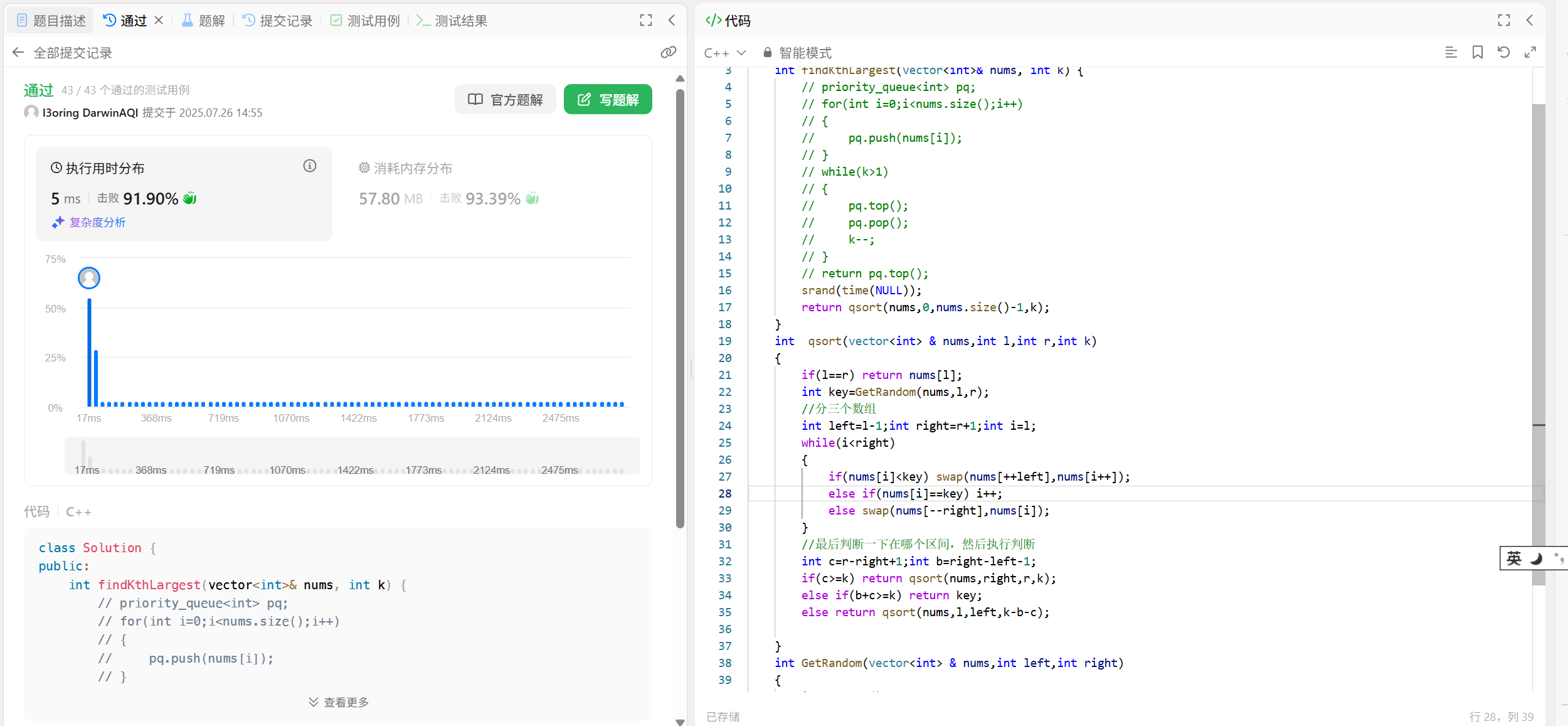
int  qsort2(vector<int>& nums, int l, int r, int k);
int GetRandom(vector<int>& nums, int left, int right);int findKthLargest(vector<int>& nums, int k) {srand(time(NULL));return qsort2(nums, 0, nums.size() - 1, k);
}
int  qsort2(vector<int>& nums, int l, int r, int k)
{if (l == r) return nums[l];//若數組中只有一個元素，這個只要是進入了qsort這個函數，則數組區間一定存在int key = GetRandom(nums, l, r);//分三個數組int left = l - 1; int right = r + 1; int i = l;while (i < right){if (nums[i] < key) swap(nums[++left], nums[i++]);else if (nums[i] == key) i++;else swap(nums[--right], nums[i]);}//最后判斷一下在哪個區間，然后執行判斷int c = r - right + 1; int b = right - left - 1;if (c >= k) return qsort2(nums, right, r, k);else if (b + c >= k) return key;else return qsort2(nums, l, left, k - b - c);//這里別忘了return}
int GetRandom(vector<int>& nums, int left, int right)
{int r = rand();return nums[r % (right - left + 1) + left];
}
int main()
{vector<int> nums = { 3,2,1,5,6,4 };int k = 2;cout << findKthLargest(nums, k) << endl;return 0;
}

哇，這個的代碼量也是挺多的。

45.4 總結反思

這里涉及到了幾個問題，我會在最后一個問題全部說清楚。

?46. 劍指offer 40.最小的k

46.1 題目解析：

這道題目也是屬于topk問題，只不過是尋找一個范圍k。

?46.2 算法思路：

解法一：可以使用排序方法，然后找出前k個小的元素即可（時間復雜度為O（n*logn））

解法二：利用堆排序（找最小的，用大根堆）（時間復雜度為O（n*logk））。

解法三就是使用快速選擇算法了：（時間復雜度為O（n））

依舊是數組分三塊加上隨機選擇基準值

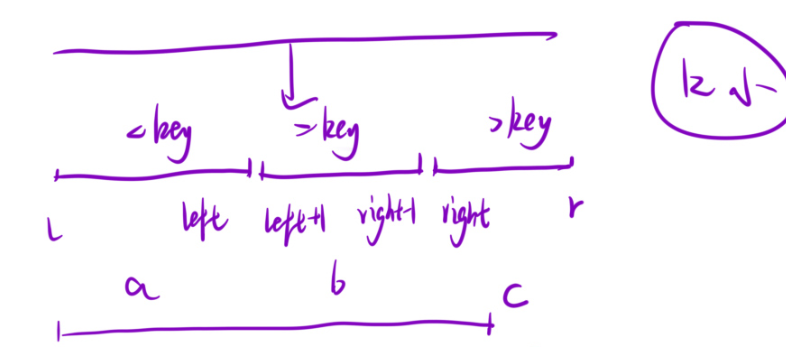
1.若a>k,前k小在a里面，去[l,left]中尋找最小的k個元素。

2.a+b>=k,此時第一種情況一定不成立，那么k>=a,又因為b區間內都是相同的元素，所以此時可以直接返回了。因為b內元素都是相同的，不需要再去找前k-a個小的了。

3.若第一種與第二種情況都不成立。那么就去[right,r]內去找最小的k-a-b個元素即可。

這里快就快在，他沒有排序（這個里面只是小于基準值，大于基準值，可能小于基準值里面的順序不是排好的）。所以它管你是小于還是大于，直接找到前k個小的元素即可。

46.3 代碼演示：

void qsort(vector<int>& nums, int l, int r, int k);
int getRandom(vector<int>& nums, int l, int r);vector<int> getLeastNumbers(vector<int>& nums, int k)
{srand(time(NULL));qsort(nums, 0, nums.size() - 1, k);return { nums.begin(), nums.begin() + k };
}
void qsort(vector<int>& nums, int l, int r, int k)
{if (l == r) return;// 1. 隨機選擇?個基準元素+數組分三塊int key = getRandom(nums, l, r);int left = l - 1, right = r + 1, i = l;while (i < right){if (nums[i] < key) swap(nums[++left], nums[i++]);else if (nums[i] == key) i++;else swap(nums[--right], nums[i]);}// [l, left][left + 1, right - 1] [right, r]// 2. 分情況討論int a = left - l + 1, b = right - left - 1;if (a > k) qsort(nums, l, left, k);else if (a + b >= k) return ;//直接return是因為最上面已經有return了， return { nums.begin(), nums.begin() + k };//且這個是void返回值else qsort(nums, right, r, k - a - b);
}
int getRandom(vector<int>& nums, int l, int r)
{return nums[rand() % (r - l + 1) + l];
}
int main()
{vector<int> nums = { 2,5,7,4 };int k =1 ;vector<int> outcome = getLeastNumbers(nums, k);for (auto& e : outcome){cout << e << "";}cout << endl;return 0;
}

好，咱們看44題里面是l>=r,而第45，46題里面都是l==r，為什么呢？

那么咱們要先知道，為什么排序的時候會有>=?

關鍵點

快速排序（Quicksort）?的目標是?完全排序數組，需要處理所有子區間。

分區邏輯?不同：

分區后遞歸?[l, left]?和?[right, r]。

可能出現?空區間：

如果所有元素 ≤?key，則?left?可能等于?r，導致?[right, r]?為空。

如果所有元素 ≥?key，則?right?可能等于?l，導致?[l, left]?為空。

為什么需要?l >= r？

快速排序的遞歸調用?不保證區間非空：

可能遞歸到?[l, left]?時?left < l（區間無效）。

需要?if (l >= r)?提前終止無效遞歸。

示例

假設?nums = [1, 1, 1]：

分區后?key = 1，left = -1，right = 3。

遞歸?[0, -1]（無效）和?[3, 2]（無效）。

需要?if (l >= r)?避免無限遞歸。

?

主要就是解決這個無效的區間的問題。

那么為什么后面兩個不需要大于呢？因為后面兩個快速選擇算法，假如，都是元素相同的數組，那么[right,r]是無效的區間對吧，但是第一次調用qsort的時候就已經返回了，它不會進入遞歸，知道吧，所第二次并不會出現[right,r]這個區間，那么排序就不同了，排序是不管怎樣，都要遞歸，所以說，排序算法才需要>=,就是為了處理遞歸的時候的無效區間。

等于的時候是，數組中只有一個元素的時候。

還有一個問題就是：會發現，當返回的是數組的時候，直接return就可以了。那是因為前面已經有了return。