題意：給出一棵樹，按照以下方式操作
對于當前的所有任意子樹，選出任何一個點從中刪除，然后作為新子樹的根插入到新的樹中，以此遞歸往復，直到原來的樹中節點全部進入新樹，問新樹最多有多少個葉子節點。
然后如果根節點只有一個聯通的點，那么自己也算葉子

思路：Codeforces Global Round 26 (A - E) - Lu_xZ - 博客園

1.首先對于題意進行解析，這個操作是在干什么，然后發現，任意相鄰的節點不能同時為葉子節點，然后如果我們把葉子節點歸為一類，就會發現所有的葉子節點就是最大獨立集
最大獨立集：選出的點集中，任何一個子集都不滿足在原圖上可以互相抵達
舉例：1-2-3-4-5-6，1作為根節點可以跟3連，2就變成了子節點，4-5-6作為新的子樹
也就是說為什么發現的，任何一個點想成為葉子節點，只要在當前子樹中選擇一個相鄰節點，自己就可以變成葉子節點

2.發現是最大獨立集，那么接下來該如何是好？因為任何一個點都可能成為根節點，于是乎考慮換根dp，這個應該要稍微靠一點感覺……
任何一個節點的子樹所選中的狀態不會因為另外一邊子樹的狀態受影響，這是換根dp的關鍵，因為這樣才能順序的求出

3.于是乎開始dp，首先求出假設某一個節點是根節點的子樹選擇情況，這里就默認選1了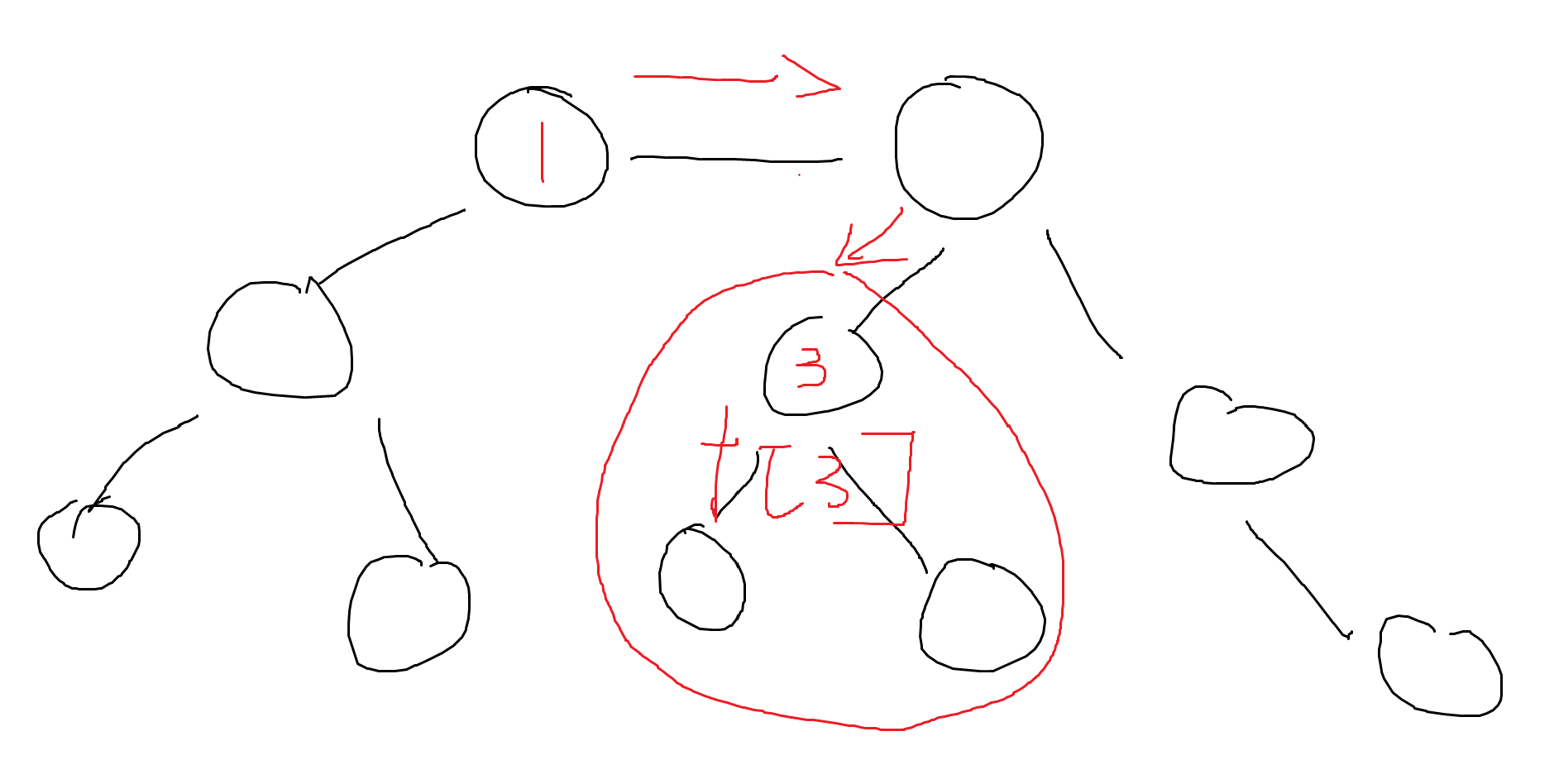

?f[3]代表3節點的情況，但是要分類f[3][0/1]，代表圖中形狀的子樹3節點作為葉子節點和不是葉子節點的情況
之后得到狀態轉移方程
f[x][0]+=max(f[u][0],f[u][1])? ?當前節點不是葉子節點，那么相鄰節點可以是葉子節點也可以不是
f[x][1]+=f[u][0]? ? 當前節點是葉子節點，相鄰節點只能不是葉子節點

接下來換根

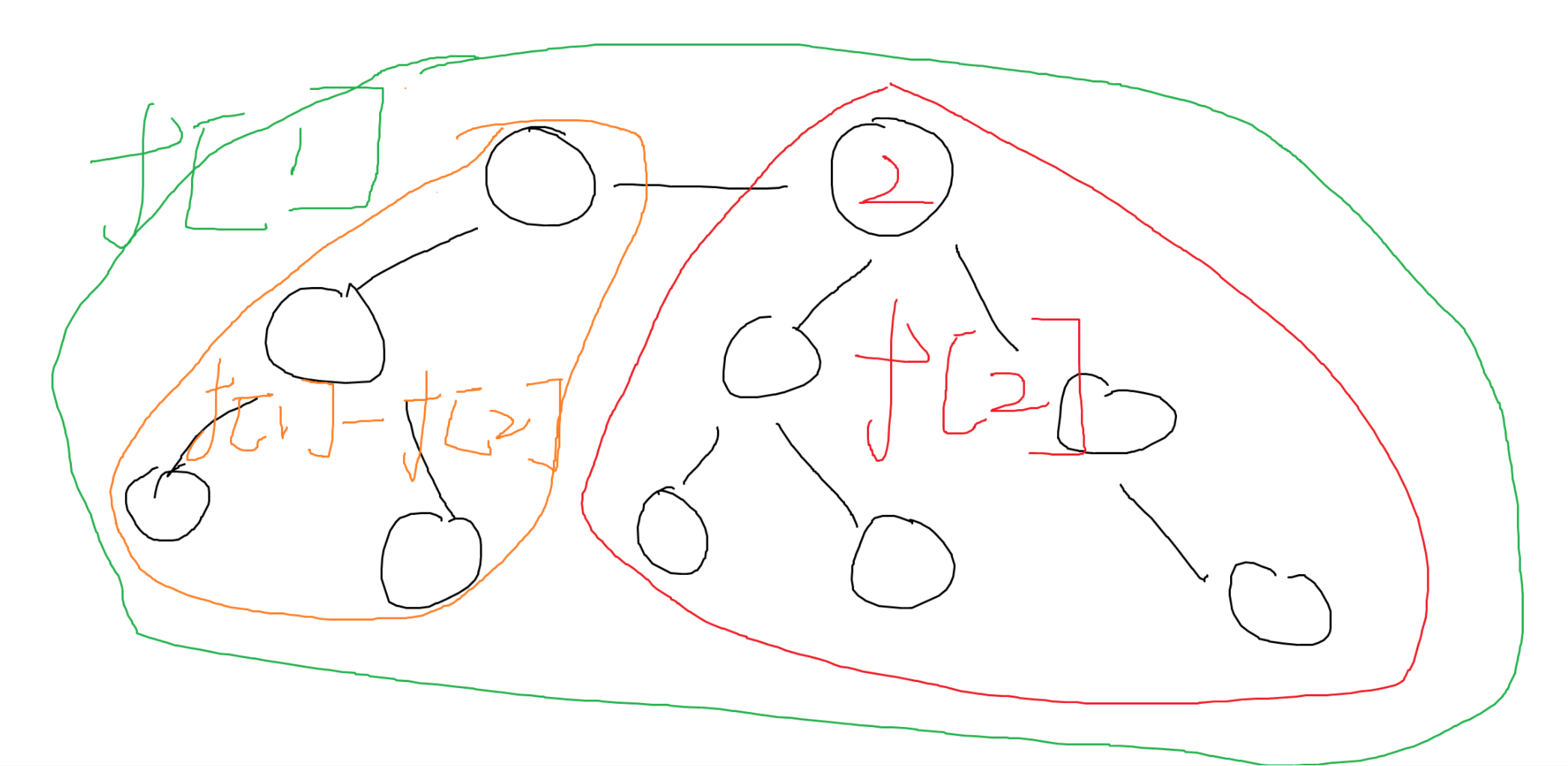
假設以2為根，f[2]所擁有的狀態只是紅色部分子樹，而另一邊就可以由父節點減去當前子樹得到
然后在此基礎上進行拼接，就完成了換根的操作
然后因為另一邊子樹只受到子樹根節點的影響，所以才能進行換根dp
我們將橙色區域稱為temp（f[1]-f[2]）
那么新的dp轉移
g[x][0]=std::max(g[fa][1],f[x][0]+temp);? ?g[fa][1]其實跟f[2][0]+(f[1]-f[2])[1]是一致的，然后另一種拼接求最多的那個
g[x][1]=temp+f[x][1];
完成dp的狀態轉移
最后求答案g[x][0]+(ve[x].size()==1);?
ve[x].size()==1是因為根節點本身可能也是葉子節點，但在dp的過程中，自己作為葉子節點是不可以的，是別人作為非葉子節點的，自己才可以選擇作為葉子節點，根作為第一個節點沒有能力選擇一個父節點作為非葉子節點，只能是自己，先有非葉子節點，才有葉子節點
任何一個點想成為葉子節點，只要在當前子樹中選擇一個相鄰節點，自己就可以變成葉子節點

掃描完成全部，那么本道題就結束了

代碼

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define IOS                       \std::ios::sync_with_stdio(0); \std::cin.tie(0);              \std::cout.tie(0)const int N = 3e5 + 5;
const int INF = 1e18;
const int MOD = 998244353;
// const int MOD=1e9+7;
// const int MOD=100003;
const int maxn=5e5+10;std::vector<int> ve[N];
int f[N][2];
int g[N][2];void dfs(int x,int fa){f[x][0]=0;f[x][1]=1;for(auto i : ve[x]){if(i==fa) continue;dfs(i,x);f[x][1]+=f[i][0];f[x][0]+=std::max(f[i][0],f[i][1]);}
}int ans=0;
void dfs2(int x,int fa){int temp=g[fa][0]-std::max(f[x][0],f[x][1]);g[x][1]=temp+f[x][1];g[x][0]=std::max(g[fa][1],f[x][0]+temp);temp=g[x][0]+(ve[x].size()==1);ans=std::max(ans,temp);for(auto i : ve[x]){if(i==fa) continue;dfs2(i,x);}
}void solve(){int n;std::cin >> n;ans=0;for(int i=1;i<=n;i++){ve[i].clear();f[i][0]=f[i][1]=g[i][0]=g[i][1]=0;}for(int i=1;i<n;i++){int x,y;std::cin >> x >> y;ve[x].push_back(y);ve[y].push_back(x);}    dfs(1,0);g[1][0]=f[1][0];g[1][1]=f[1][1];ans=g[1][0]+(ve[1].size()==1);for(auto i : ve[1])dfs2(i,1);std::cout << ans << '\n';
}signed main()
{IOS;int t = 1;std::cin >> t;while (t--){solve();}
}