不需要手撕實現，下節紅黑樹同理。

一、AVL的概念

• AVL樹是最先發明的自平衡二叉查找樹，AVL是一顆空樹，或者具備下列性質的二叉搜索樹（AVL樹的前提條件）：它的左右子樹都是AVL樹，且左右子樹的高度差的絕對值不超過1（AVL樹的條件）。AVL樹是一顆高度平衡搜索二叉樹，通過控制高度差去控制平衡。
• AVL樹得名于它的發明者G. M. Adelson-Velsky和E. M. Landis，是兩個前蘇聯的科學家，他們在1962年的論文《An algorithm for the organization of information》中發表了它。
• AVL樹實現這里我們引入一個平衡因子(balance factor)的概念，每個結點都有一個平衡因子，任何結點的平衡因子等于右子樹的高度減去左子樹的高度，也就是說任何結點的平衡因子等于0/1/-1，AVL樹并不是必須要平衡因子，但是有了平衡因子可以更方便我們去進行觀察和控制樹是否平衡，就像一個風向標一樣。
• 思考一下為什么AVL樹是高度平衡搜索二叉樹，要求高度差不超過1，而不是高度差是0呢？0不是更好的平衡嗎？畫圖分析我們發現，不是不想這樣設計，而是有些情況是做不到高度差是0的。比如一棵樹是2個結點，4個結點等情況下，高度差最好就是1，無法做到高度差是0。
• AVL樹整體結點數量和分布和完全二叉樹類似，高度可以控制在O(logN) ，那么增刪查改的效率也可以控制在O(logN) ，相比二叉搜索樹有了本質的提升。

二、AVL樹的實現

1、AVL樹的結構

template<class K, class V>
struct AVLTreeNode
{// 需要parent指針，后續更新平衡因子可以看到pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right; AVLTreeNode<K, V>* _parent;int _bf;// balance factorAVLTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){ }
};template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:// ...
private:Node* _root = nullptr;
};

2、AVL樹的插入

（1）、AVL樹插入一個值的大概過程

1. 插入一個值按二叉搜索樹規則進行插入。
2. 新增結點以后，不會影響所有的結點，只會影響祖先結點的高度，也就是可能會影響部分祖先路徑上的結點的平衡因子，所以更新從新增結點->根結點路徑上的平衡因子，實際中最壞情況下要更新到根，有些情況更新到中間就可以停止了，具體情況我們下面再詳細分析。
3. 更新平衡因子過程中沒有出現問題，則插入結束。
4. 更新平衡因子過程中出現不平衡，對不平衡子樹旋轉，旋轉后本質調平衡的同時，本質降低了子樹的高度，不會再影響上一層，所以插入結束。

（2）、平衡因子更新

更新原則

• 平衡因子 = 右子樹高度-左子樹高度。
• 只有子樹高度變化才會影響當前結點平衡因子。
• 插入結點，會增加高度，所以新增結點在parent的右子樹，parent的平衡因子++，新增結點在parent的左子樹，parent平衡因子--。
• parent所在子樹的高度是否變化決定了是否會繼續往上更新。

更新停止條件

• 更新后parent的平衡因子等于0，更新中parent的平衡因子變化為 -1->0 或者 1->0，說明更新前parent子樹一邊高一邊低，新增的結點插入在低的那邊，插入后parent所在的子樹高度不變，不會影響parent的父親結點的平衡因子，更新結束。
• 更新后parent的平衡因子等于 1 或 -1，更新前更新中parent的平衡因子變化為 0->1 或者 0->-1，說明更新前parent子樹兩邊一樣高，新增的插入結點后，parent所在的子樹一邊高一邊低，parent所在的子樹符合平衡要求，但是高度增加了 1，會影響parent的父親結點的平衡因子，所以要繼續向上更新。
• 更新后parent的平衡因子等于 2 或 -2，更新前更新中parent的平衡因子變化為 1->2 或者 -1->-2，說明更新前parent子樹一邊高一邊低，新增的插入結點在高的那邊，parent所在的子樹高的那邊更高了，破壞了平衡，parent所在的子樹不符合平衡要求，需要旋轉處理，旋轉的目標有兩個：1、把parent子樹旋轉平衡。2、降低parent子樹的高度，恢復到插入結點以前的高度。所以旋轉后也不需要繼續往上更新，插入結束。
• 不斷更新，更新到根，根的平衡因子是 1 或 -1 也停止了。

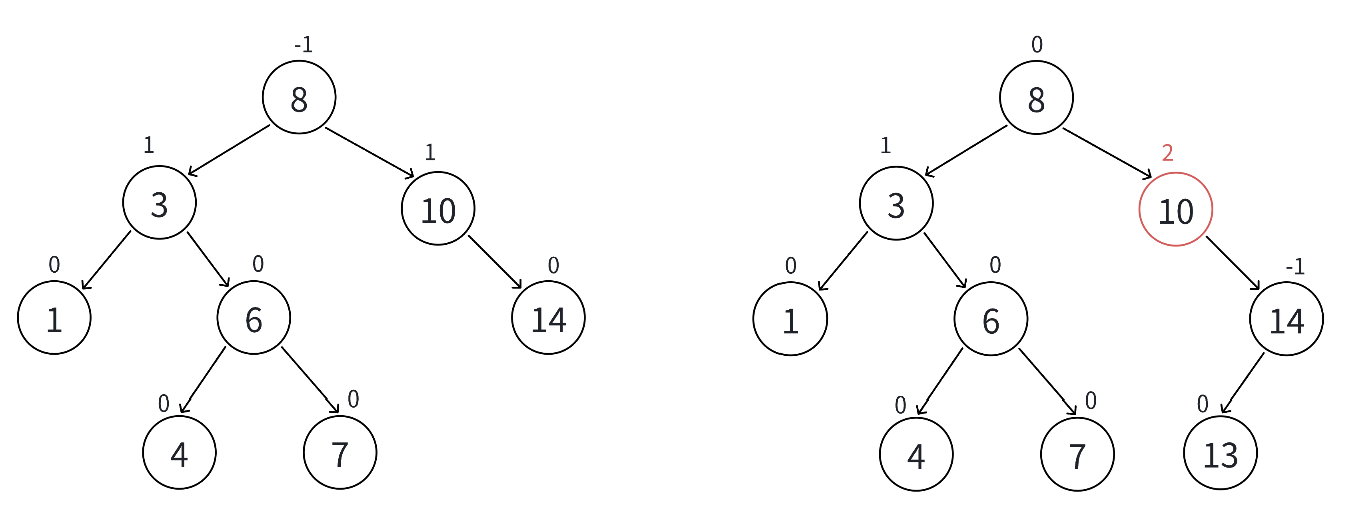
更新到10結點，平衡因子為2，10所在的子樹已經不平衡，需要旋轉處理

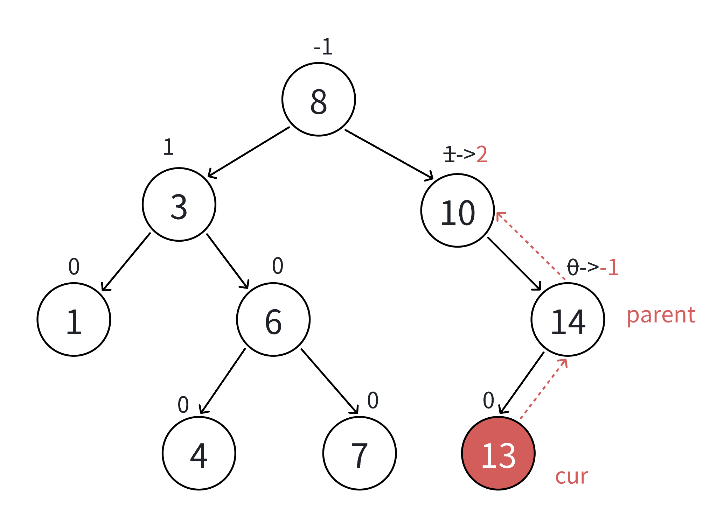
更新到中間結點，3為根的子樹高度不變，不會影響上一層，更新結束

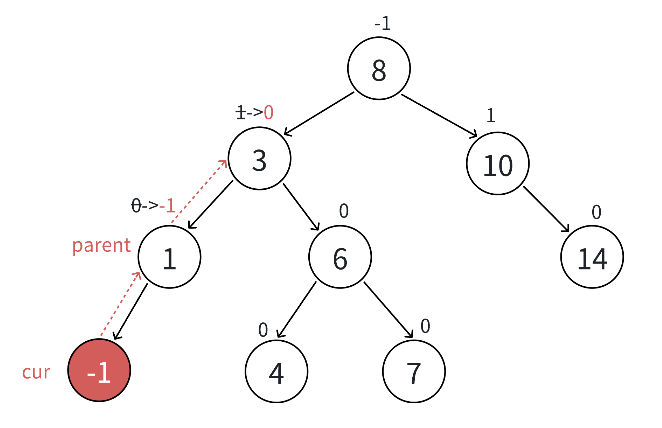
最壞更新到根停止

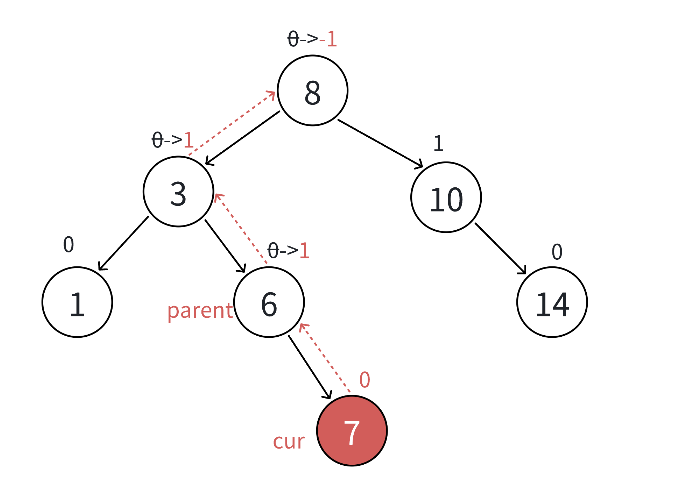
插入結點及更新平衡因子的代碼實現

bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first)parent->_right = cur;elseparent->_left = cur;cur->_parent = parent;// 更新平衡因子while (parent){// 更新平衡因子if (cur == parent->_left)parent->_bf--;elseparent->_bf++;if (parent->_bf == 0){// 更新結束break;}else if (parent->_bf == 1 || parent->_bf == -1){// 繼續往上更新cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){// 不平衡了，旋轉處理break;}else{// 相當于程序走到這里就報錯assert(false);}}return true;
}

3、旋轉

（1）、旋轉的原則

1. 保持搜索樹的規則。
2. 讓旋轉的樹從不滿足變平衡，其次降低旋轉樹的高度。
   旋轉總共分為四種，左單旋/右單旋/左右雙旋/右左雙旋。
   說明：下面的圖中，有些結點我們給的是具體值，如10和5等結點，這里是為了方便講解，實際中是什么值都可以，只要大小關系符合搜索樹的性質即可。

（2）、右單旋

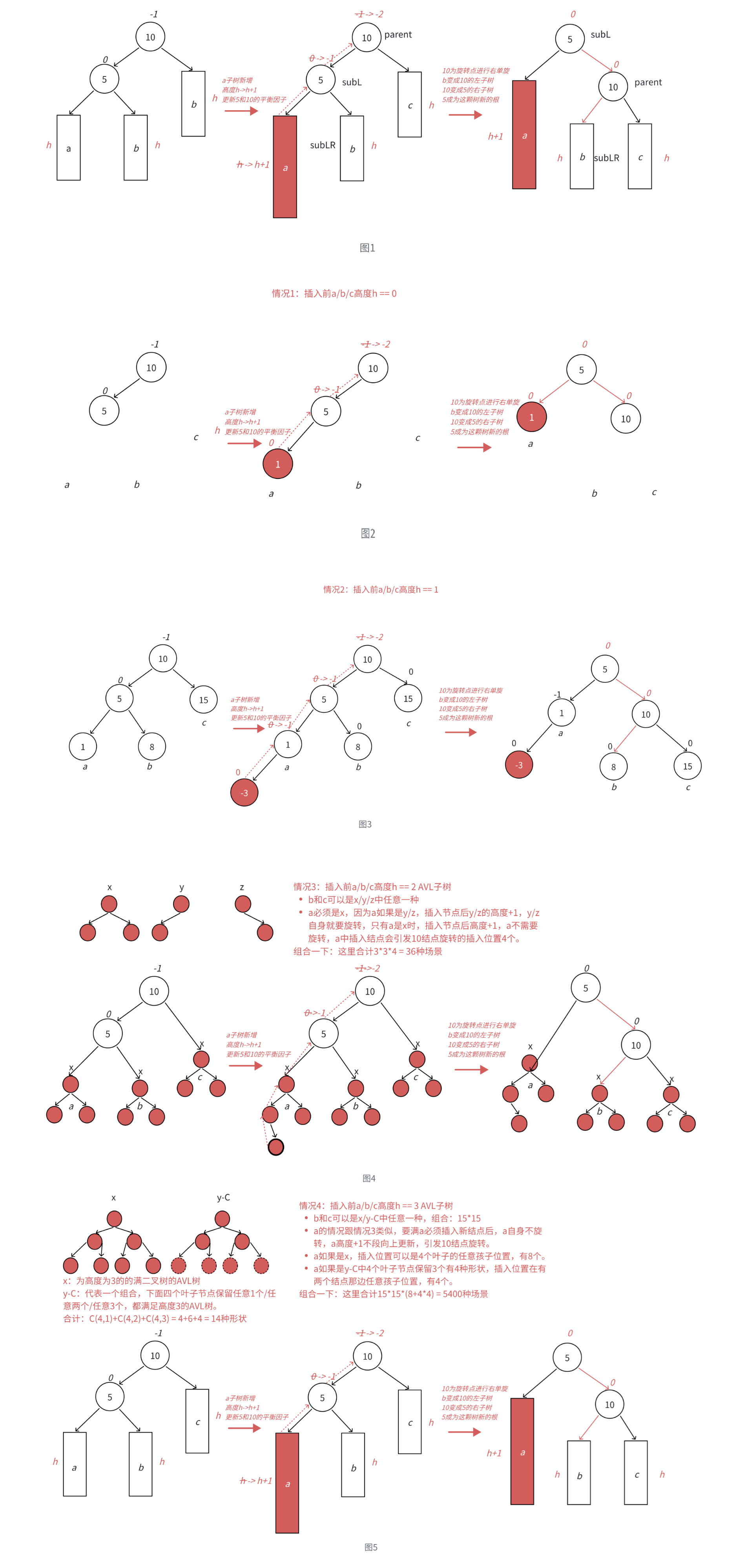
• 本圖1展示的是10為根的樹，有a/b/c抽象為三棵高度為h的子樹(h>=0)，a/b/c均符合AVL樹的要求。10可能是整棵樹的根，也可能是一個整棵樹中局部的子樹的根。這里a/b/c是高度為h的子樹，是一種概括抽象表示，他代表了所有右單旋的場景，實際右單旋形態有很多種，具體圖2/圖3/圖4/圖5進行了詳細描述。
• 在a子樹中插入一個新結點（在a子樹的左/右邊都可以插入），導致a子樹的高度從h變成h+1，不斷向上更新平衡因子，導致10的平衡因子從-1變成-2，10為根的樹左右高度差超過1，違反平衡規則。10為根的樹左邊太高了，需要往右邊旋轉，控制兩棵樹的平衡。
• 旋轉核心步驟，因為5 < b子樹的值 < 10，將b變成10的左子樹，10變成5的右子樹，5變成這棵樹新的根（右單旋三步驟），符合搜索樹的規則，控制了平衡，同時這棵的高度恢復到了插入之前的h+2，符合旋轉原則。如果插入之前10整棵樹的一個局部子樹，旋轉后不會再影響上一層，插入結束了。

圖4：b和c各有3種高度為2的AVL子樹，子樹a有4種插入位置。
圖5：y-C（y杠C），下面葉子結點保留4個就是x。b和c各有15（y-C14種再加上x一種）種情況。

（3）、右單旋代碼實現

void RotateR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;// 需要注意除了要修改孩子指針指向，還要修改父親parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;parent->_parent = subL;Node* parentParent = parent->_parent;// parent有可能是整棵樹的根，也可能是局部的子樹的根// 如果是整棵樹的根，要修改_root// 如果是局部的指針要跟上一層鏈接if (parentParent == nullptr){_root = subL;subL->_parent = nullptr;}else{if (parentParent->_left == parent){parentParent->_left = subL;}else{parentParent->_right = subL;}subL->_parent = parentParent;}parent->_bf = subL->_bf = 0;
}

（4）、左單旋

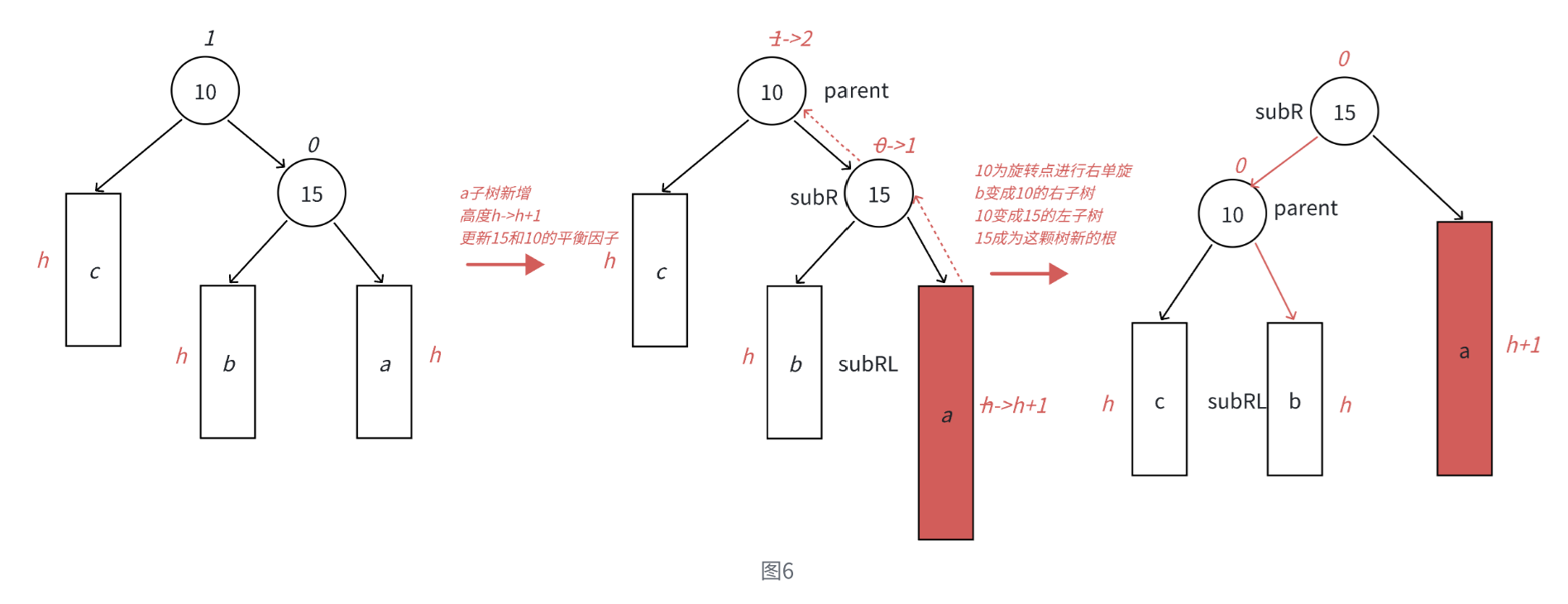
• 本圖6展示的是10為根的樹，有a/b/c抽象為三棵高度為h的子樹(h>=0)，a/b/c均符合AVL樹的要求。10可能是整棵樹的根，也可能是一個整棵樹中局部的子樹的根。這里a/b/c是高度為h的子樹，是一種概括抽象表示，他代表了所有右單旋的場景，實際右單旋形態有很多種，具體跟上面左旋類似。
• 在a子樹中插入一個新結點，導致a子樹的高度從h變成h+1，不斷向上更新平衡因子，導致10的平衡因子從1變成2，10為根的樹左右高度差超過1，違反平衡規則。10為根的樹右邊太高了，需要往左邊旋轉，控制兩棵樹的平衡。
• 旋轉核心步驟，因為10 < b子樹的值 < 15，將b變成10的右子樹，10變成15的左子樹，15變成這棵樹新的根，符合搜索樹的規則，控制了平衡，同時這棵的高度恢復到了插入之前的h+2，符合旋轉原則。如果插入之前10整棵樹的一個局部子樹，旋轉后不會再影響上一層，插入結束了。

（5）、左單旋代碼實現

void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;parent->_parent = subR;Node* parentParent = parent->_parent;if (parentParent == nullptr){_root = subR;subR->_parent = nullptr;}else{if (parentParent->_left == parent){parentParent->_left = subR;}else{parentParent->_right = subR;}subR->_parent = parentParent;}parent->_bf = subR->_bf = 0;
}

（6）、左右雙旋

左右雙旋特點：parent和subL的平衡因子是異號。

通過圖7和圖8可以看到，左邊高時，如果插入位置不是在a子樹，而是插入在b子樹，b子樹高度從h變成h+1，引發旋轉，右單旋無法解決問題，右單旋后，我們的樹依舊不平衡。右單旋解決的純粹的左邊高，但是插入在b子樹中，10為跟的子樹不再是單純的左邊高，對于10是左邊高，但是對于5是右邊高，需要用兩次旋轉才能解決，以5為旋轉點進行一個左單旋，以10為旋轉點進行一個右單旋，這棵樹這棵樹就平衡了。

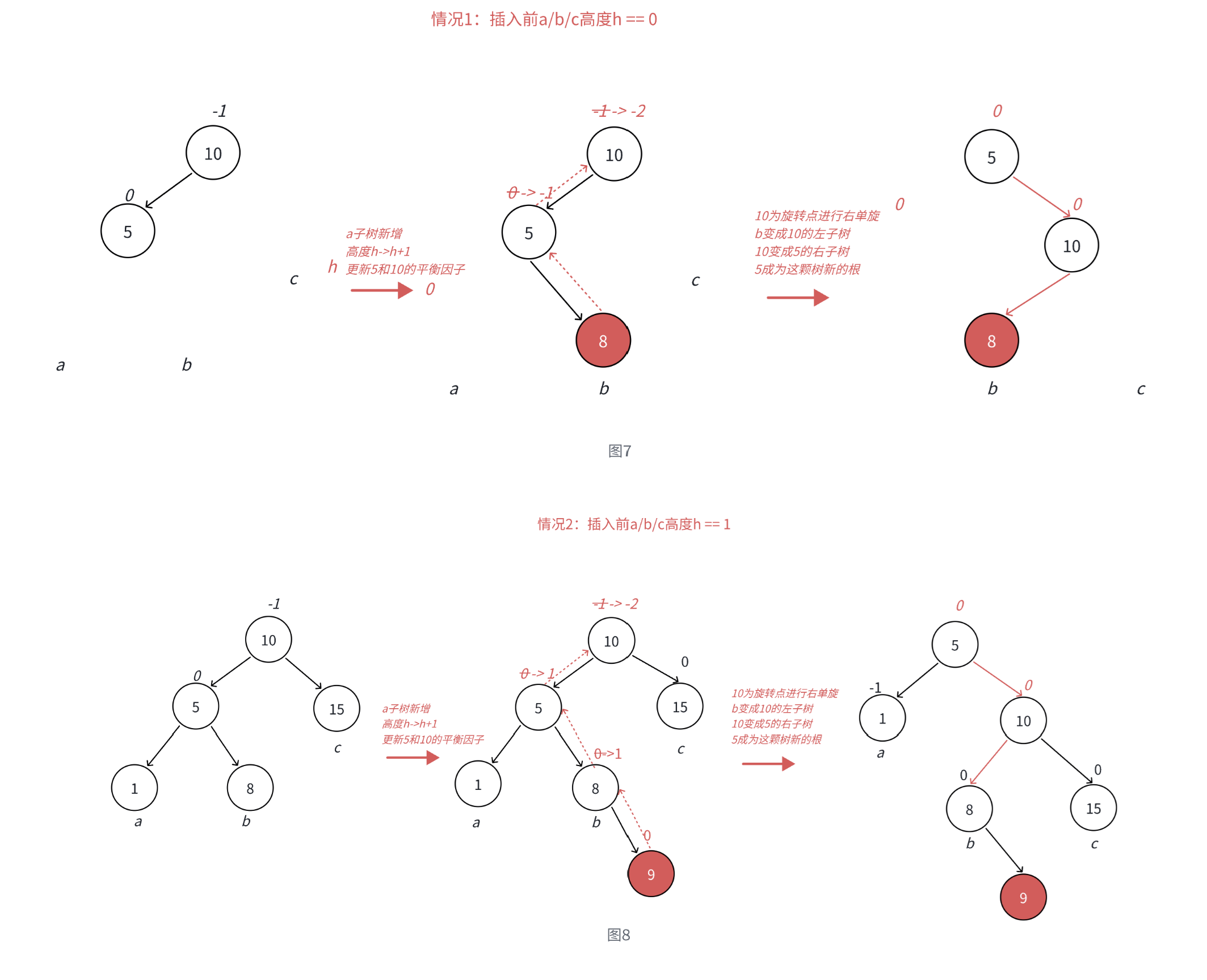
• 圖7和圖8分別為左右雙旋中h==0和h==1具體場景分析，下面我們將a/b/c子樹抽象為高度h的AVL子樹進行分析，另外我們需要把b子樹的細節進一步展開為8和高度為h-1的左右子樹e和f，因為我們要對b的父親5為旋轉點進行左單旋，左單旋需要動b樹中的左子樹。b子樹中新增結點的位置不同，平衡因子更新的細節也不同，通過觀察8的平衡因子不同，這里我們要分三個場景討論。
• 場景1：h >= 1時，新增結點插入在e子樹，e子樹高度從h-1并為h并不斷更新8->5->10平衡因子，引發旋轉，其中8的平衡因子為-1，旋轉后8和5平衡因子為0，10平衡因子為1。
• 場景2：h >= 1時，新增結點插入在f子樹，f子樹高度從h-1變為h并不斷更新8->5->10平衡因子，引發旋轉，其中8的平衡因子為1，旋轉后8和10平衡因子為0，5平衡因子為-1。
• 場景3：h == 0時，a/b/c都是空樹，b自己就是一個新增結點，不斷更新5->10平衡因子，引發旋轉，其中8的平衡因子為0，旋轉后8和10和5平衡因子均為0。

從結果看，b子樹的根變成了整個樹的根結點，左子樹e是5的右孩子，右子樹f是10的左孩子。

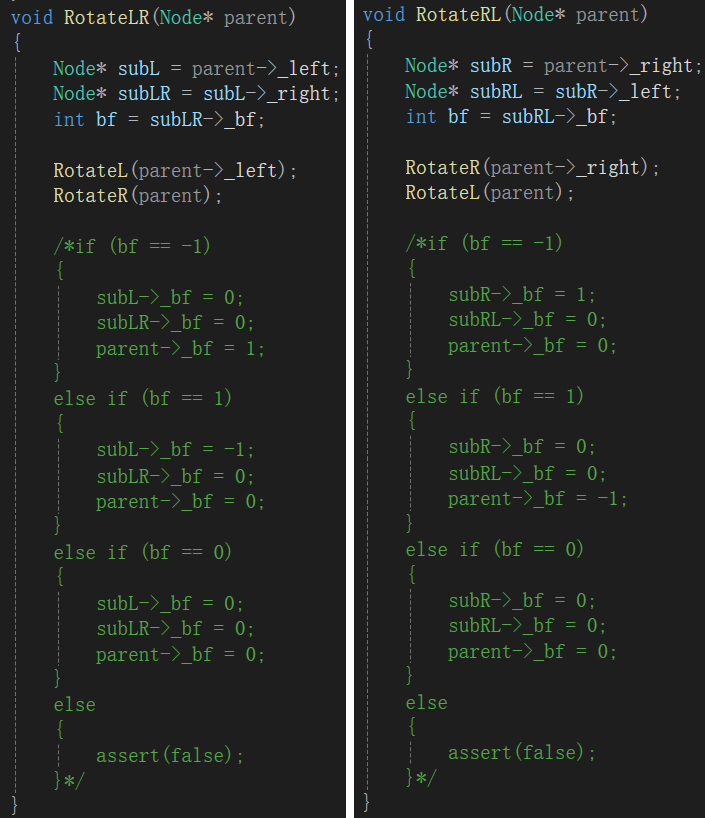
（7）、左右雙旋代碼實現

void RotateLR(Node* parent)
{Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == -1){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 1;}else if (bf == 1){subL->_bf = -1;subLR->_bf = 0;parent->_bf = 0;}else if (bf == 0){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 0;}else{assert(false);}
}

（8）、右左雙旋

右左雙旋特點：parent和subR的平衡因子是異號。

• 跟左右雙旋類似，下面我們將a/b/c子樹抽象為高度h的AVL子樹進行分析，另外我們需要把b子樹的細節進一步展開為12和高度為h-1的左右子樹e和f，因為我們要對b的父親15為旋轉點進行右單旋，右單旋需要動b樹中的右子樹。b子樹中新增結點的位置不同，平衡因子更新的細節也不同，通過觀察12的平衡因子不同，這里我們要分三個場景討論。
• 場景1：h >= 1時，新增結點插入在e子樹，e子樹高度從h-1變為h并不斷更新12->15->10平衡因子，引發旋轉，其中12的平衡因子為-1，旋轉后10和12平衡因子為0，15平衡因子為1。
• 場景2：h >= 1時，新增結點插入在f子樹，f子樹高度從h-1變為h并不斷更新12->15->10平衡因子，引發旋轉，其中12的平衡因子為1，旋轉后15和12平衡因子為0，10平衡因子為-1。
• 場景3：h == 0時，a/b/c都是空樹，b自己就是一個新增結點，不斷更新15->10平衡因子，引發旋轉，其中12的平衡因子為0，旋轉后10和12和15平衡因子均為0。

從結果看，b子樹的根變成了整個樹的根結點，左子樹e是10的右孩子，右子樹f是15的右孩子。

（9）、右左雙旋代碼實現

void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == -1){subR->_bf = 1;subRL->_bf = 0;parent->_bf = 0;}else if (bf == 1){subR->_bf = 0;subRL->_bf = 0;parent->_bf = -1;}else if (bf == 0){subR->_bf = 0;subRL->_bf = 0;parent->_bf = 0;}else{assert(false);}
}

4、AVL樹的查找

按二叉搜索樹邏輯實現即可，搜索效率為 O(logN)

Node* Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_kv.first < key){cur = cur->_right;}else if (cur->_kv.first > key){cur = cur->_left;}else{return cur;}}return nullptr;
}

5、AVL樹平衡檢測

我們實現的AVL樹是否合格，我們通過檢查左右子樹高度差的的程序進行反向驗證，同時檢查一下結點的平衡因子更新是否出現了問題。

int _Height(Node* root)
{if (nullptr == root)return 0;int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
bool _IsBalanceTree(Node* root)
{// 空樹也是AVL樹if (nullptr == root)return true;// 計算pRoot結點的平衡因子：即pRoot左右子樹的高度差int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);int diff = rightHeight - leftHeight;// 如果計算出的平衡因子與pRoot的平衡因子不相等，// 或者pRoot平衡因子的絕對值超過1，則一定不是AVL樹if (abs(diff) >= 2){cout << root->_kv.first << "高度差異常" << endl;return false;}if (root->_bf != diff){cout << root->_kv.first << "平衡因子異常" << endl;return false;}// pRoot的左和右如果都是AVL樹，則該樹一定是AVL樹return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);
}

// 測試代碼
void TestAVLTree1()
{AVLTree<int, int> t;// 常規的測試用例int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };// 特殊的帶有雙旋場景的測試用例//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };for (auto e : a){t.Insert({ e, e });}t.InOrder();cout << t.IsBalanceTree() << endl;
}

雙旋測試用例下，若是把雙旋代碼屏蔽平衡因子的部分：

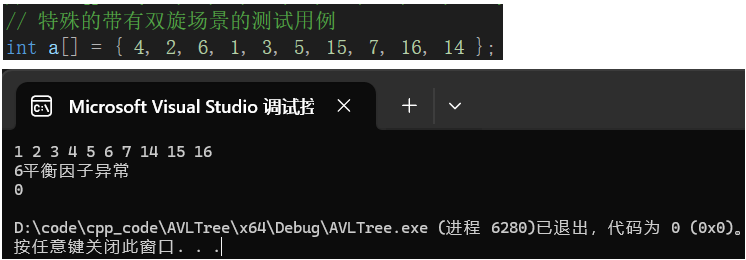
調試畫出二叉樹：

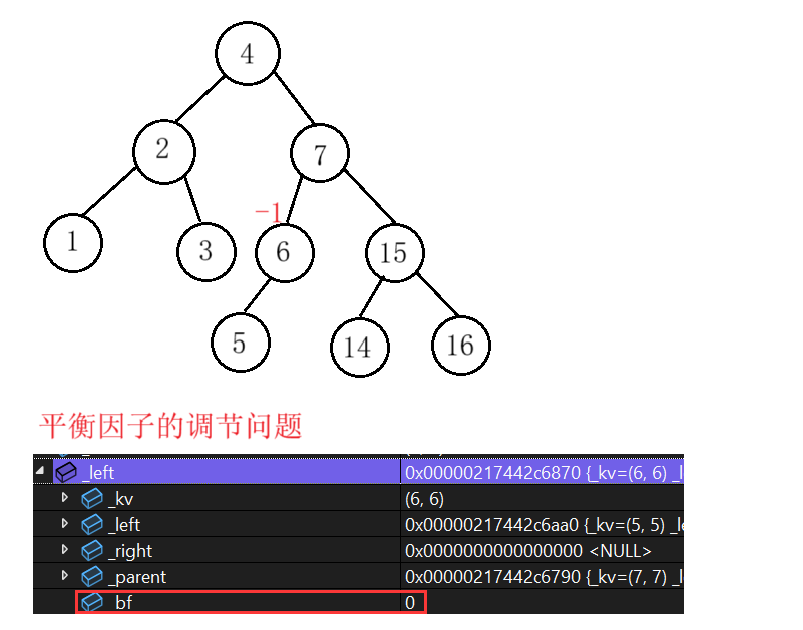
若不知道是雙旋代碼出現了問題，那么這種錯誤怎么查出來呢？——插入一個值就打印一個值。

發現是因為插入14時才引發的平衡因子異常問題，所以就去調試14的問題：

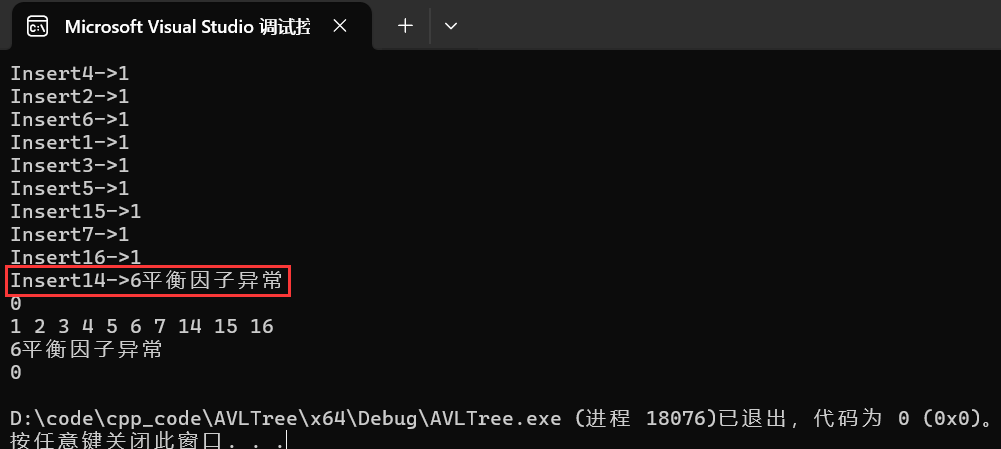
但是可能會出現跳過14的問題，或者數據量龐大時可能會按很久的F5鍵，這時可以用上條件斷點。

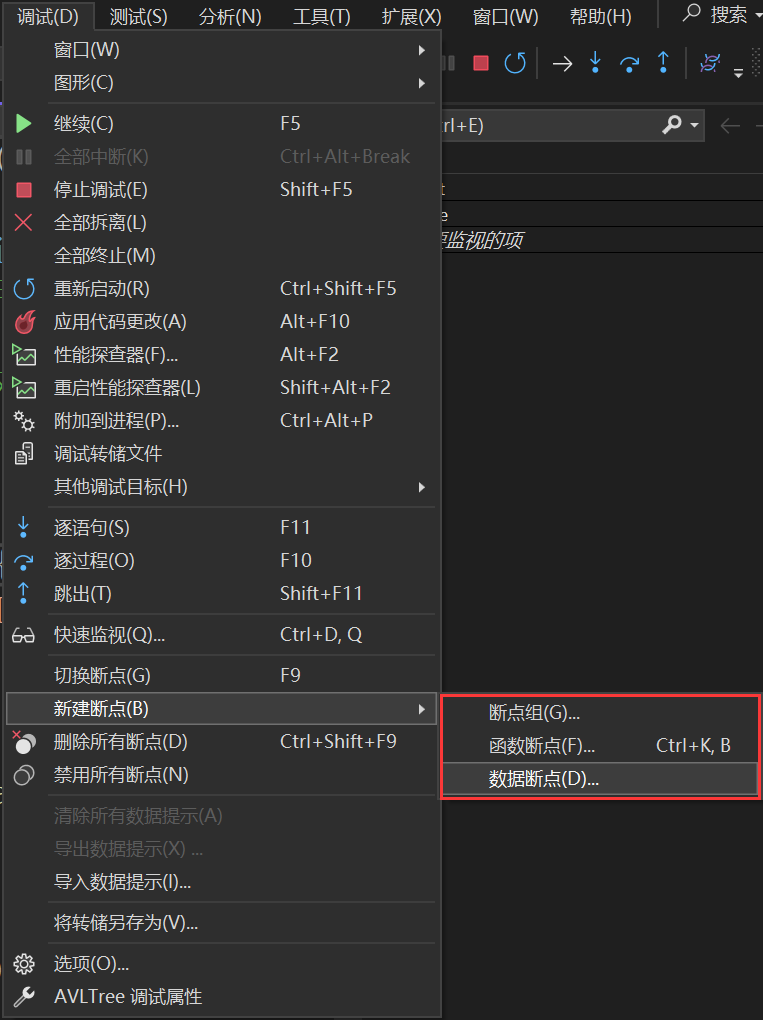
但是斷點有時麻煩，還有更簡單的方法，空語句斷不住，所以可以隨便寫一個語句，這里寫的就是定義變量x的語句：

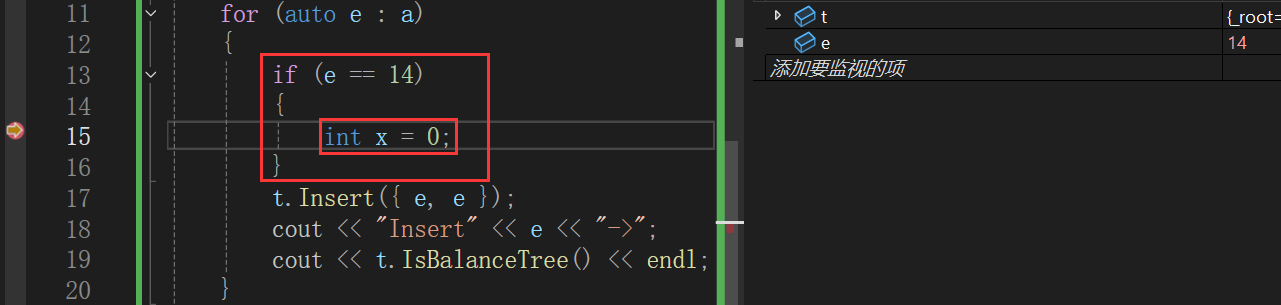
再把這棵樹畫出來，插入14結點并更新平衡因子：

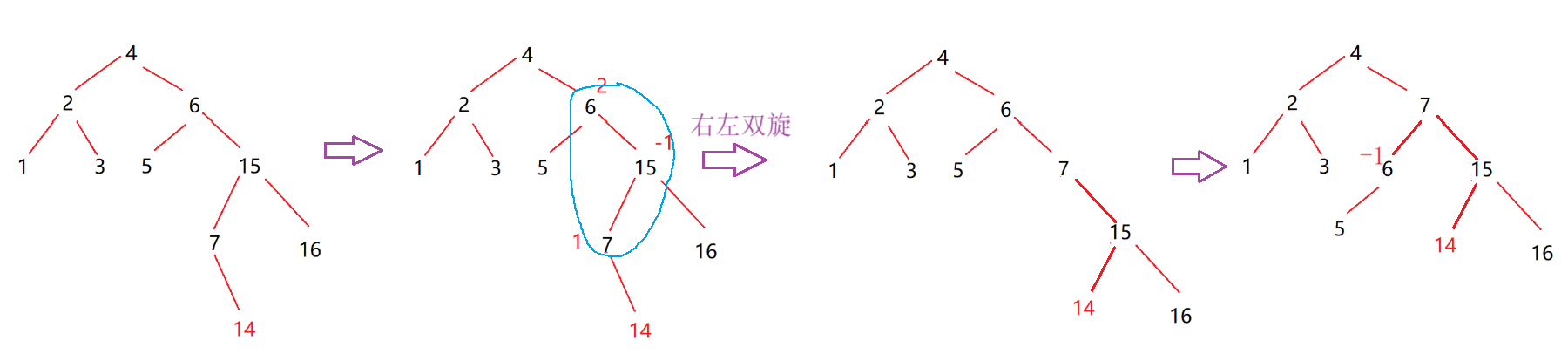
最后發現是平衡因子調節的問題。

雙旋平衡因子代碼注釋解開再運行沒問題：

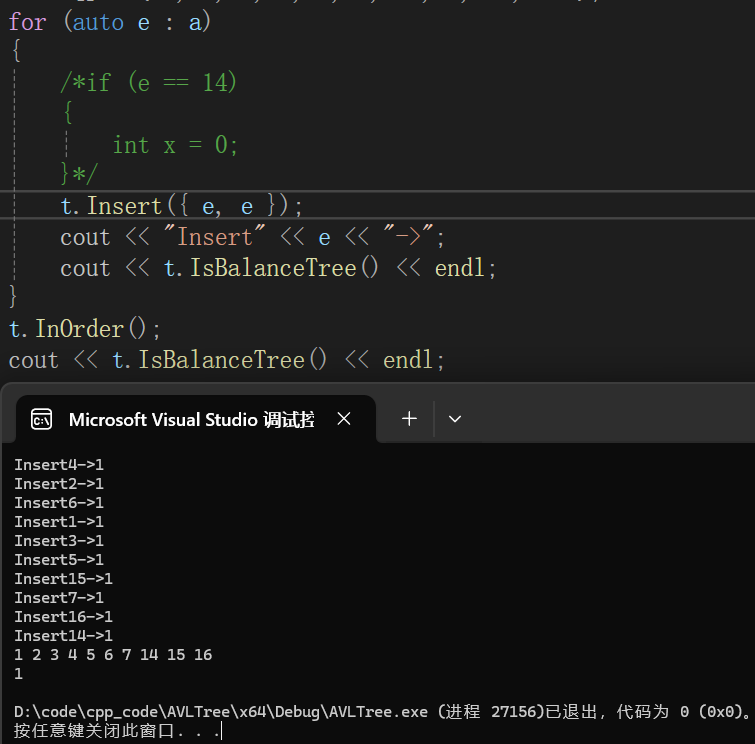
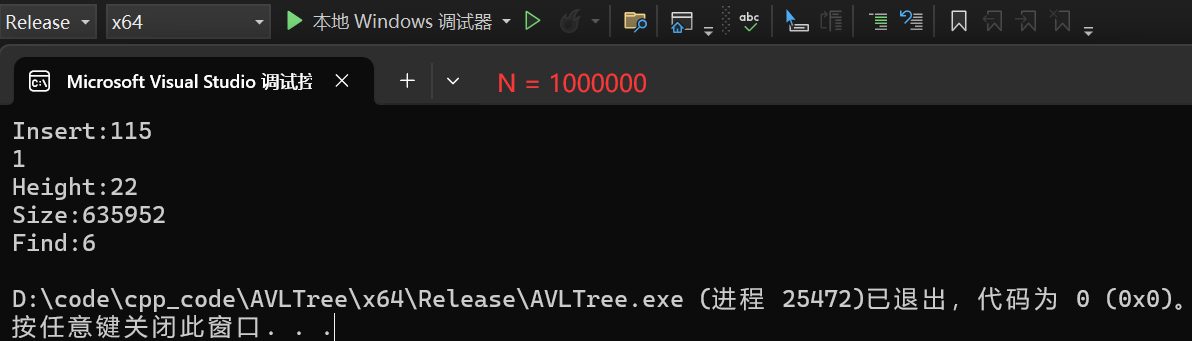
AVL樹（二叉樹）越往下增加一層所得的結點總數是越多的，導致高度變化不快，進而搜索效率很高。

// 插入一堆隨機值，測試平衡，順便測試一下高度和性能等
void TestAVLTree2()
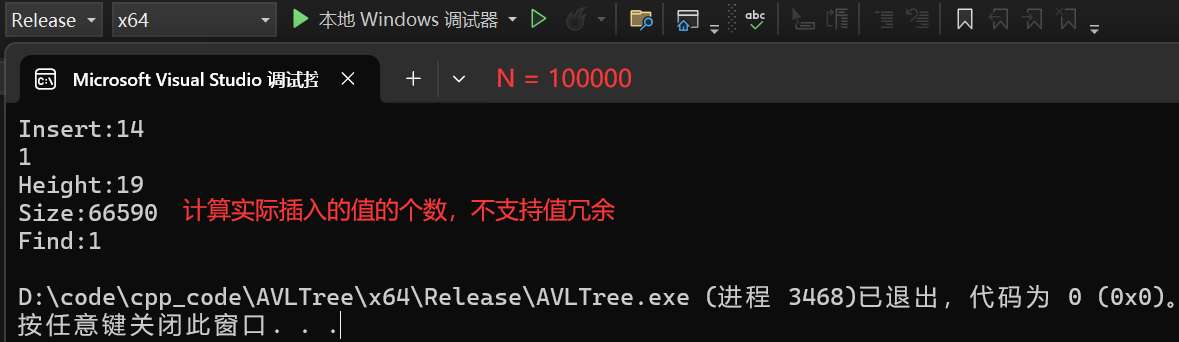
{const int N = 100000;vector<int> v;v.reserve(N);srand(time(0));for (size_t i = 0; i < N; i++){v.push_back(rand() + i);}size_t begin2 = clock();AVLTree<int, int> t;for (auto e : v){t.Insert(make_pair(e, e));}size_t end2 = clock();// 測試Insert的性能cout << "Insert:" << end2 - begin2 << endl;cout << t.IsBalanceTree() << endl;cout << "Height:" << t.Height() << endl;cout << "Size:" << t.Size() << endl;size_t begin1 = clock();// 確定在的值/*for (auto e : v){t.Find(e);}*/// 隨機值for (size_t i = 0; i < N; i++){t.Find((rand() + i));}size_t end1 = clock();// 測試Find的性能cout << "Find:" << end1 - begin1 << endl;
}

6、AVL樹的刪除

AVL樹的刪除本章節不做講解，也不需要掌握，有興趣的可參考：《殷人昆 數據結構：用面向對象方法與C++語言描述》中講解。

三、AVL樹完整實現代碼

// AVLTree.h
#include <iostream>
#include <assert.h>
using namespace std;template<class K, class V>
struct AVLTreeNode
{// 需要parent指針，后續更新平衡因子可以看到pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right; AVLTreeNode<K, V>* _parent;int _bf;// balance factorAVLTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){ }
};template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);return true;}Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first)parent->_right = cur;elseparent->_left = cur;cur->_parent = parent;// 更新平衡因子while (parent){// 更新平衡因子if (cur == parent->_left)parent->_bf--;elseparent->_bf++;if (parent->_bf == 0){// 更新結束break;}else if (parent->_bf == 1 || parent->_bf == -1){// 繼續往上更新cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){// 單旋就是純粹的左邊高或者右邊高// 雙旋就是不是純粹的一邊高，比如：右子樹高，右子樹里面又是左子樹高// 不平衡了，旋轉處理if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}break;}else{assert(false);}}return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_kv.first < key){cur = cur->_right;}else if (cur->_kv.first > key){cur = cur->_left;}else{return cur;}}return nullptr;}bool IsBalanceTree(){return _IsBalanceTree(_root);}void InOrder(){_InOrder(_root);cout << endl;}int Height(){return _Height(_root);}// 計算實際插入的值的個數，不支持值冗余int Size(){return _Size(_root);}
private:int _Size(Node* root){return root == nullptr ? 0 :_Size(root->_left) + _Size(root->_right) + 1;}int _Height(Node* root){if (nullptr == root)return 0;int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}bool _IsBalanceTree(Node* root){// 空樹也是AVL樹if (nullptr == root)return true;// 計算pRoot結點的平衡因子：即pRoot左右子樹的高度差int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);int diff = rightHeight - leftHeight;// 如果計算出的平衡因子與pRoot的平衡因子不相等，// 或者pRoot平衡因子的絕對值超過1，則一定不是AVL樹if (abs(diff) >= 2){cout << root->_kv.first << "高度差異常" << endl;return false;}if (root->_bf != diff){cout << root->_kv.first << "平衡因子異常" << endl;return false;}// pRoot的左和右如果都是AVL樹，則該樹一定是AVL樹return _IsBalanceTree(root->_left) && _IsBalanceTree(root->_right);}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;// 需要注意除了要修改孩子指針指向，還要修改父親parent->_left = subLR;if (subLR)subLR->_parent = parent;Node* parentParent = parent->_parent;subL->_right = parent;parent->_parent = subL;// parent有可能是整棵樹的根，也可能是局部的子樹// 如果是整棵樹的根，要修改_root// 如果是局部的指針要跟上一層鏈接if (parentParent == nullptr){_root = subL;subL->_parent = nullptr;}else{if (parentParent->_left == parent){parentParent->_left = subL;}else{parentParent->_right = subL;}subL->_parent = parentParent;}parent->_bf = subL->_bf = 0;}void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* parentParent = parent->_parent;subR->_left = parent;parent->_parent = subR;if (parentParent == nullptr){_root = subR;subR->_parent = nullptr;}else{if (parentParent->_left == parent){parentParent->_left = subR;}else{parentParent->_right = subR;}subR->_parent = parentParent;}parent->_bf = subR->_bf = 0;}void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == -1){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 1;}else if (bf == 1){subL->_bf = -1;subLR->_bf = 0;parent->_bf = 0;}else if (bf == 0){subL->_bf = 0;subLR->_bf = 0;parent->_bf = 0;}else{assert(false);}}void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == -1){subR->_bf = 1;subRL->_bf = 0;parent->_bf = 0;}else if (bf == 1){subR->_bf = 0;subRL->_bf = 0;parent->_bf = -1;}else if (bf == 0){subR->_bf = 0;subRL->_bf = 0;parent->_bf = 0;}else{assert(false);}}
private:Node* _root = nullptr;
};

// Test.cpp
#include "AVLTree.h"
#include <vector>
// 測試代碼
void TestAVLTree1()
{AVLTree<int, int> t;// 常規的測試用例——只有單旋//int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };// 特殊的帶有雙旋場景的測試用例int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };for (auto e : a){/*if (e == 14){int x = 0;}*/t.Insert({ e, e });/*cout << "Insert" << e << "->";cout << t.IsBalanceTree() << endl;*/}t.InOrder();cout << t.IsBalanceTree() << endl;
}
// 插入一堆隨機值，測試平衡，順便測試一下高度和性能等
void TestAVLTree2()
{const int N = 100000;vector<int> v;v.reserve(N);srand(time(0));for (size_t i = 0; i < N; i++){v.push_back(rand() + i);}size_t begin2 = clock();AVLTree<int, int> t;for (auto e : v){t.Insert(make_pair(e, e));}size_t end2 = clock();// 測試Insert的性能cout << "Insert:" << end2 - begin2 << endl;cout << t.IsBalanceTree() << endl;cout << "Height:" << t.Height() << endl;cout << "Size:" << t.Size() << endl;size_t begin1 = clock();// 確定在的值/*for (auto e : v){t.Find(e);}*/// 隨機值for (size_t i = 0; i < N; i++){t.Find((rand() + i));}size_t end1 = clock();// 測試Find的性能cout << "Find:" << end1 - begin1 << endl;
}
int main()
{TestAVLTree2();return 0;
}