1. 排序算法

1. 歸并排序

1.1 普通歸并排序

歸并排序比較適用于處理較大規模的數據，且比較消耗內存。所以小規模的序列，一般不使用歸并排序。

基本思想：

? 就是“分治”思想，先將序列元素拆解，然后歸并，即合并相鄰有序子序列。

1.2 優化后的歸并排序（TimSort）

自適應、穩定、高效的排序算法，源自合并排序和插入排序。

我們來進行歸并排序的時候，就進行了許多沒必要的“分”，因為有些子序列本來就是有序的了，隨而也導致沒必要的“治”。TimSort就是為了解決這一缺陷而生。

Timsort的思想是，“分”的時候，直接從左往右，劃分成各種不同長度的、有序的子序列（每個子序列叫做一個run，），然后對這些子序列進行歸并，這樣一來，復雜度就大大降低了。

有序的子序列（Run）：遞增的序列或者是嚴格遞減的序列（保證算法的穩定性，遞減的序列需要進行翻轉）。

minRun：最小的有序子序列的長度。如果有一個run的長度沒有達到minrun，那就要從run序列后面的元素進行二分插入放入到run中，直到run的長度達到最小minrun。

minrun的選擇：16-64之間，數組的長度/minrun 略小于等于2的次冪。

子序列合并：

? 需要使用棧。從第一個run開始依次入棧，每入棧一次，就要檢查：

直到棧中所有run都滿足上述要求，繼續將下一個run放入到棧中。最終合并成一個。（為什么上圖這么合并：如果違反了下面的兩條規則，則Y與X、Z中的較小者合并。規則使得合并保持近似平衡，同時在延遲合并以實現平衡）

2. 插入排序

2.1 直接插入排序

基本思想：序列分為兩部分，一部分有序，一部分無序，不斷從無序的部分選元素出來，插入到有序的部分。（一開始是認為第一個元素是有序的部分，其他元素都是無序的部分）

插入排序一般應用于數據量較小的序列排序中。因為插入排序在小數組中已經表現的很好了。

2.2 二分插入排序

與直接插入排序不同點是：直接插入排序是待插入的元素依次和前一個元素進行比較、交換，直到滿意位為止；二分插入排序是先從有序數組中通過二分查找確定待插入的位置，然后將后面的元素依次后移一位，并將帶插入元素插入其中。減少了比較次數。

2.3 成對插入排序

在直接插入排序里面，我們在進行插入的時候，需要在每次循環時，不斷與有序的元素進行比較，直到找到合適位置。而比較次數與移位次數是衡量一個算法優劣的標準。

成對插入排序是為了減少比較次數而生。

• 基本思想：
  第一步：在無序部分拿兩個元素a1，a2，并調整使a1>a2；
  第二步：a1往左比較，找到合適位置后插入；
  第三步：a2只需在a1的左邊進行比較（a1>a2）,找到合適的位置插入即可。

3. 快速排序

3.1 單軸快速排序

基本思想：
第一步：選其中一個元素出來作為軸。
第二步：兩邊同時開始遍歷，比軸小的元素放在左邊，比軸大的元素放在右邊。
第三步：對上面被軸分開的兩個序列，進行遞歸處理，重復執行一二步。最終得到一個有序序列

3.2 雙軸快排

單軸很多時候可能會遇到較差的情況就是選取的元素可能是最大的或者最小的元素，這樣元素就沒辦法將元素進行劃分，時間復雜度也就變成了$T(n)=T(n?1)+O(n),T(n)=O(n^2)$?。

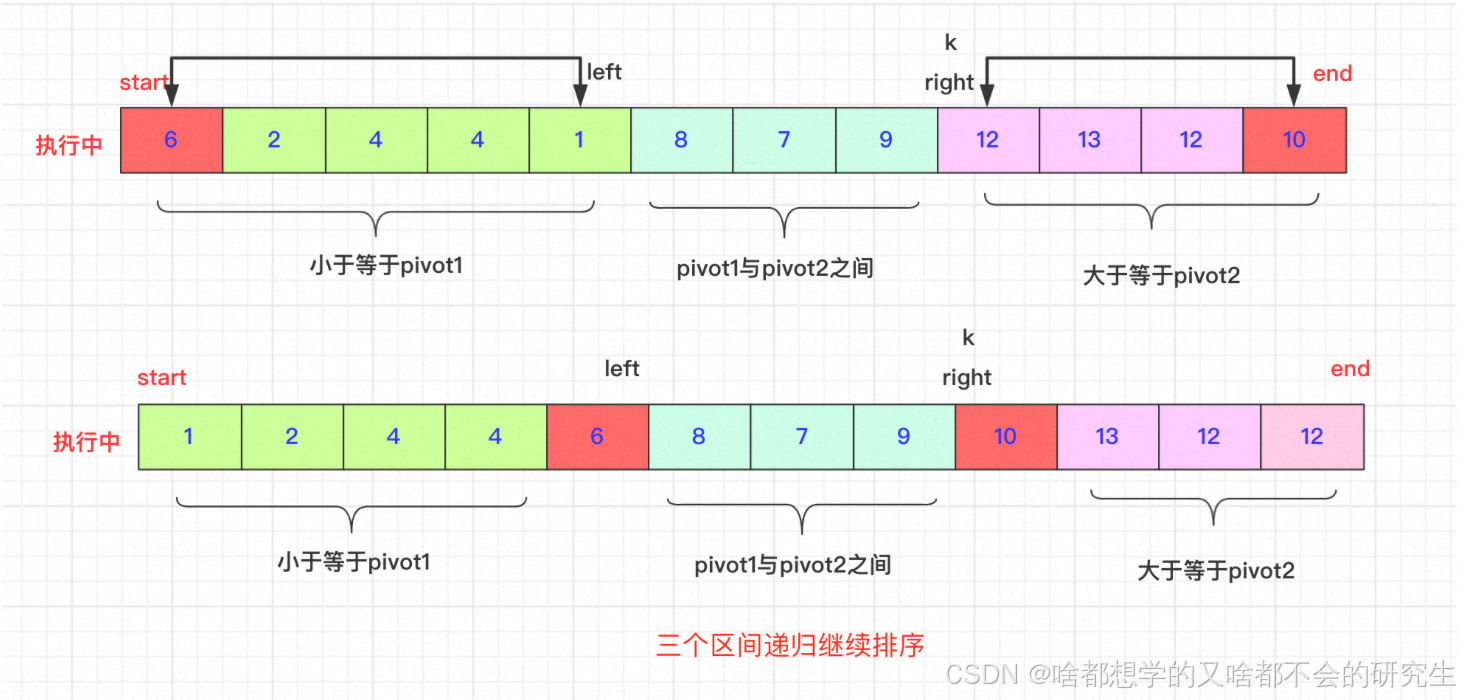
雙軸快排，顧名思義，就是按兩個軸，分成三個區。對于單軸快排，選取的軸是最大的或者最小的元素就會導致排序性能降低。對于雙軸快排，只有兩個軸一個選取最大，一個選取最小，才會使性能降低，這種概率比快排的概率小太多了。所以，雙軸快排的優化力度還是挺大的。

選取待排序的最左側、最右側的兩個數作為軸pivot1、pivot2，并且保證pivot1< pivot2，不滿足就交換。通過交換數組中的元素，小于pivot1的元素放在pivot1左側，大于pivot2的元素放在最右側，在兩者之間的放在中間。

然后，依次遞歸下去。

交換過程：

start和end一直不動，直到排好在進行交換。

4. 計數排序

計數排序適用于元素個數遠大于元素種數的情況，適用于Short、Byte、Char等元素種數較少的類型。

基本思想：
①：先創建一個length為元素種數的數組count，里面的元素全部為0。
②：遍歷要排序的序列，根據序列元素大小a找到數組count的位置，對count[a]+=1;
(舉個例子：若剛好遍歷到的元素是55，則找到count[55]+=1)
③：從左到右遍歷count[]，元素不是0的位置都拿出來，根據count[a]拿多少個。
④：最終得到有效序列。

2. 樹

1. 紅黑樹（Red Black Tree）

1.1 紅黑樹的定義或者是約束條件

1. 節點要么是紅色要么是黑色
2. 根節點必須是黑色
3. 葉子節點掛兩個空節點(邏輯上)是黑色
4. 每個紅色節點有兩個黑色子節點，推導出一條路徑上不能有兩個連續的紅色節點
5. 每條路徑上必須有相同數量的黑色節點

1.2 紅黑樹添加節點：

待插入節點是紅色的，然后按照二叉搜索將待插入節點插入到葉子結點。

父節點叔節點	紅色	黑色
紅色	變色（父節點、叔節點變黑，祖節點變紅。然后把祖節點當做新插入的節點遞歸上述操作）	無需操作
黑色	旋轉（旋轉完成之后，再根據變色原則，進行變色，這個過程中同樣也會遇到旋轉，但你已經明白了旋轉的規律了。）	無需操作

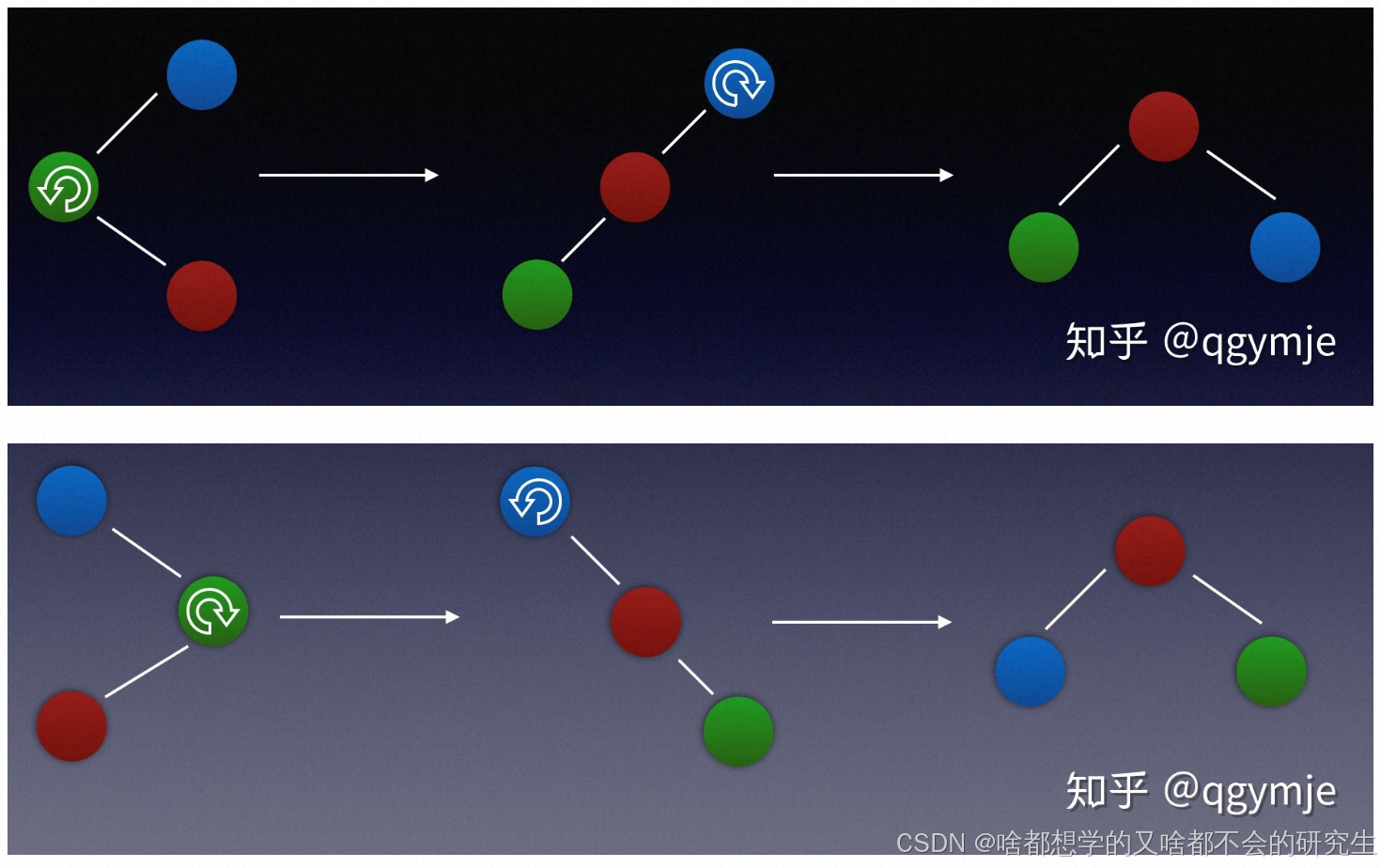
四種旋轉情況（根據剛插入節點、父節點、祖節點的位置）：

1.3 紅黑樹刪除節點

首先看一下二叉搜索樹刪除節點操作：

先說一下如何刪除二叉樹查找樹的節點吧。總共有三種情況

1.被刪除的節點是葉子節點，這時候只要把這個節點刪除，再把指向這個節點的父節點指針置為空就行

2.被刪除的節點有左子樹，或者有右子樹，而且只有其中一個，那么只要把當前刪除節點的父節點指向被刪除節點的左子樹或者右子樹就行。

3.被刪除的節點既有左子樹而且又有右子樹，這時候需要把左子樹的最右邊的節點或者右子樹最左邊的節點提到被刪除節點的位置。

紅黑樹中刪除一個節點，遇到的各種情形就是其子節點的狀態和顏色的組合，子節點狀態共有3種：無子節點、有一個子節點、有兩個子節點，顏色有紅色和黑色兩種，所以共會有6種組合。

1. 紅黑樹刪除節點也要滿足二叉搜索樹的左小右大。因此，刪除兩個節點的情況和二叉搜索樹的情況一樣，轉換成刪除0個或者1個節點的情況。
2. 只有一個子節點的情況，該節點不能是紅色，只能是黑色。

可能出現的組合：

組合1：被刪節點無子節點，且被刪結點為紅色

這是最簡單的一種情況，直接將節點刪除即可，不破壞任何紅黑樹的性質

組合2：被刪結點無子結點，且被刪結點為黑色

這是最復雜的情況，我們稍后再討論

組合3：被刪結點有一個子結點，且被刪結點為黑色

這種組合下，被刪結點node的另一個子結點value必然為紅色，此時直接將node刪掉，用value代替node的位置，并將value著黑即可。

再論組合2：被刪結點無子結點，且被刪結點為黑色

因為刪除黑色結點會破壞紅黑樹的性質5，所以為了不破壞性質5，將node刪除后用一個擁有額外黑色的null替代它（可以想象是將node刪除后，在這個位置放了一個黑色的權值），剩下的就是調平的過程，最終這個游離的黑色權值被扔掉，整個刪除操作完成。

然后再結合node的父結點father和其兄弟結點brother來分析。

情形一：brother為黑色，且brother有一個與其方向一致的紅色子結點son

所謂方向一致，是指brother為father的左子結點，son也為brother的左子結點；或者brother為father的右子結點，son也為brother的右子結點。

情形二：brother為黑色，且brother有一個與其方向不一致的紅色子結點son

轉換成情形1，接著操作。

情形三：brother為黑色，且brother無紅色子結點

此時若father為紅，則重新著色即可，刪除操作完成。

此時若father為黑，則重新著色，將游離的黑色權值存到father（此時father的黑色權重為2），將father作為新的結點進行情形判斷，遇到情形一、情形二，則進行相應的調整，完成刪除操作；如果沒有，則結點一直上溯，直到根結點存儲額外的黑色，此時將該額外的黑色扔掉，即完成了刪除操作。（這個情景是最難的，好好理解）

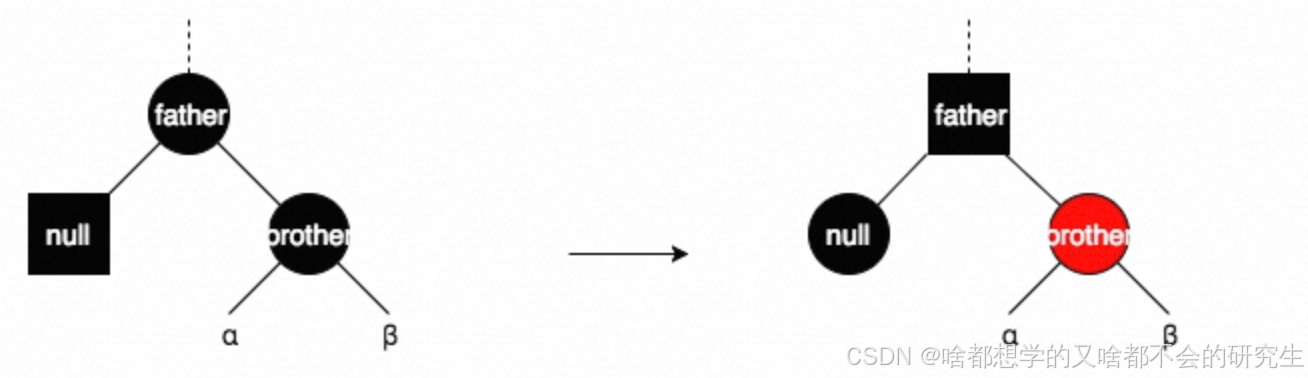
情形四：brother為紅色，則father必為黑色。

圖(i)中，將brother和father旋轉，重新上色后，變成了圖(j)，新的brother（原來的son）變成了黑色，這樣就成了情形一、二、三中的一種。
圖(i)中的情形顛倒過來，也是一樣的操作。

總而言之，基本操作原則就是：一個黑色節點被刪除之后，那么它的兄弟分支的節點分配給它一個或者是兄弟分支也減少一個，父節點從紅色變黑色。