Graph Representation Learning【圖最短路徑優化/Node2vec/Deepwalk】

文章目錄

- - Q1：
  - - 網絡性質：
    - - 1.數據讀取與鄰接表構建：
      - 2.基本特征和連通性：
    - 算法思路：
    - - 1. 廣度優先搜索（BFS）標記前驅:
      - 2. 回溯生成所有最短路徑:
    - 實驗結果：
    - 復雜度分析：
  - Q2：
  - - 算法思路：
    - - 初始化
    - 實驗結果：
    - 復雜度分析：
  - Q3：
  - - 圖表示學習：
    - 實驗結果：
    - - 結果分析：
      - ps：為什么不同距離度量的樣本區分度大有不同？
    - 別的嘗試：
  - 參考：

Q1：

DDI網絡構建無向圖并找出指定節點i和j的所有最短距離

DDI網絡可表示為：
$G_{small}=(V_{small},E_{small})\\ V_{small}=\{1,2,3,4\} \\E_{small}=\{(1,2),(1,3),(1,4),(3,4)\}$

網絡性質：

無向無權的大規模稀疏圖，我們一般用鄰接表存儲：

1.數據讀取與鄰接表構建：

? 遍歷所有邊，為每個節點維護其鄰接節點列表。對于邊 ( (u, v) )，將 ( v ) 加入 ( u ) 的鄰接列表，并將 ( u ) 加入 ( v ) 的鄰接列表。
$\text{Adj}[u] \leftarrow \text{Adj}[u] \cup \{v\}, \quad \text{Adj}[v] \leftarrow \text{Adj}[v] \cup \{u\}$

2.基本特征和連通性：

通過dfs得到圖的連通性結果如下

在這里插入圖片描述

每個節點平均連接到大約47個其他節點
這意味著整個圖是一個單一的連通組件，沒有孤立的子圖，整個網絡是完全連通的，任何兩個節點之間都存在路徑相連

以下為度數分布圖：

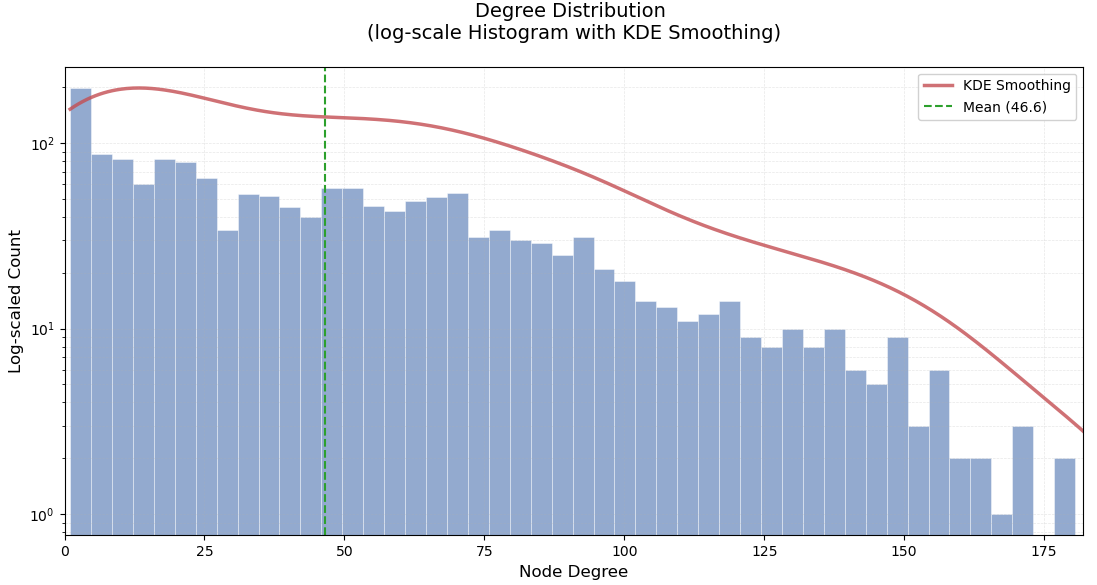
在這里插入圖片描述

算法思路：

尋找兩點之間的所有最短路徑，使用**BFS+回溯**, 因為由上面的分析可知，圖的平均度數很高，較為密集，最短路徑長度較短，所以遞歸深度不會太高。
但是在路徑回溯階段，雖然直觀易實現，但在最短路徑數量較多的情況下，遞歸深度和調用棧開銷可能迅速增長，性能下降甚至棧溢出。所以先使用顯式棧進行迭代回溯。
在回溯過程中，某些節點的路徑可能會被多次訪問。記憶化緩存可以保存已經計算過的路徑，避免再次計算。

1. 廣度優先搜索（BFS）標記前驅:

初始化距離 (d[s] = 0)，其余節點 ( d[v] = inf )。
使用隊列逐層擴展，更新節點的最短距離和前驅節點：
$\forall v \in \text{Adj}[u], \quad \text{若 } d[v] > d[u] + 1 \implies d[v] \leftarrow d[u] + 1, \ \text{prev}[v] \leftarrow \{u\} \\ \text{若 } d[v] = d[u] + 1 \implies \text{prev}[v] \leftarrow \text{prev}[v] \cup \{u\}$
當隊列為空時結束。

2. 回溯生成所有最短路徑:

從終點 ( t ) 啟動，使用顯式棧模擬遞歸過程，逐步構建所有從起點 ( s ) 到終點 ( t ) 的最短路徑。與傳統的回溯方法不同，這里我們利用記憶化搜索來緩存計算過的路徑，以減少不必要的重復計算。

使用棧中元素表示當前遍歷狀態：(當前節點, 當前路徑)。
如果當前節點是起點 s，則路徑已經完整，逆序將路徑加入結果集中。
如果當前節點不是起點，首先檢查該節點是否已經有緩存路徑（通過 memo 字典）。如果有，則直接從緩存中取出路徑；否則，遍歷當前節點的前驅節點，將所有可能的路徑推入棧中。

實驗結果：

對于（8,309）、（67,850）、（990,1256）藥物的最短路徑：
在這里插入圖片描述

使用time模塊：對于最短路徑較多的用時較少。

在這里插入圖片描述

復雜度分析：

BFS會遍歷所有邊和節點來計算最短路徑，并且回溯最短路徑時涉及到路徑構建
實際最壞時間復雜度比沒有緩存時更低，但是由于使用了記憶化搜索，減少了重復計算

$\cdot L)~~~~~\\V為節點數，E為邊數，K是路徑數量,L是路徑最大長度$

Q2：

計算所有正負藥物對的最短距離并可視化對比兩類樣本的結果

列表	數據含義	藥物對的數量
DDIpos	DDI網絡中存在相互作用的藥物對（正樣本）	1601
DDIneg	DDI網絡中沒有相互作用的藥物對（負樣本）	1601

算法思路：

不同于Q1尋找所有的最短路徑, 要計算大量節點間的最短距離，所以我們之間使用BFS即可，考慮到效率，特別是在查詢較長路徑時，嘗試雙向廣度優先搜索。
從起點和終點同時開始搜索，直到兩者相遇。這樣可以顯著減少搜索的空間，尤其是對于大的圖，因為搜索空間的半徑會從兩個方向擴展，通常比從一個方向全圖擴展要小。

初始化

定義兩個隊列 Q_s、Q_t，分別從起點 s 和終點 t 啟動：
$\text{dist}(s, s) = 0,\quad \text{dist}(t, t) = 0$
交替擴展搜索隊列：
- 從 Q_s 中取出節點 u 及其當前距離 d_s，對每個鄰居 w：
  
  $\notin \text{visited}_s \Rightarrow \text{加入 } Q_s,\quad \text{dist}(s, w) = d_s + 1$
- 從 Q_t 中取出節點 v 及其當前距離 d_t，對每個鄰居 w'：
  
  $\notin \text{visited}_t \Rightarrow \text{加入 } Q_t,\quad \text{dist}(t, w') = d_t + 1$
路徑相遇判定：
當存在某個節點
$\in \text{visited}_s \cap \text{visited}_t$
最短路徑長度為：
$\text{dist}(s, t) = \text{dist}(s, x) + \text{dist}(t, x)$
不可達判斷：
若兩個隊列均為空仍未相遇，說明 s 到 t不可達。

實驗結果：

在這里插入圖片描述

正負樣本對的距離柱狀圖如下：

正樣本對最短距離幾乎都分布在2_{4，負樣本對分布在5}6。

復雜度分析：

最短路徑長度為 d,即
$d i s t (s, t) = d$
分別從 ( s )、( t ) 同時擴展，搜索深度減半
$\bar𝑑 ，則 BFS 深度為 𝑘 時，節點數量近似為 𝑂(\bar𝑑^k)\\搜索節點數近似為：O(\bar{d}^{d/2})$

最壞情況：要遍歷整個圖，時間復雜度仍為
$O (V + E) V 為節點數， E 為邊數$
平均情況：因搜索深度減半，效率提高：

$O(\bar{d}^{d/2})$

Q3：

對藥物節點進行embedding并在嵌入空間計算可視化表征向量的歐式距離/余弦距離，并進行分析比較

圖表示學習：

Deepwalk：一張圖上隨機生成節點序列，用這些節點序列以Word2vec方法生成embedding。對比Word2vec，把每一個“詞”看做節點，得到每個節點的embedding后求兩兩embedding的余弦相似度，得到top N的近鄰排序推薦給目標節點。
Node2vec：添加控制游走方向的參數，BFS更體現結構性，DFS更體現同質性(遠端節點)
- 參數p：控制“回頭"概率
- 參數q：控制偏向BFS or DFS

實驗結果：

節點嵌入:dimensions=128,walk_length=30，num_walk=100
node2vec: 超參設置不同，對比實驗結果如下:

在這里插入圖片描述

boxplot繪制直觀展示：

結果分析：

Deepwalk：采用均勻的隨機步長探索鄰域。這樣，DeepWalk 強調的是 節點之間的共現頻率，由于沒有對鄰域進行加權或偏向某一類鄰域結構，DeepWalk 對 直接連接節點對 的敏感度相對較低，無法很好地區分局部鄰域的細節。
Node2vec:
- 當 p 值較小，q 值較大時，Node2Vec 強調 局部鄰域結構。此時，模型傾向于對 直接連接的節點對 給予較高的權重，使得正樣本（直接連接的節點對）的歐氏距離顯著小于負樣本。這使得 局部結構 更容易被區分。雖然這種設置能夠有效提高歐氏距離的區分度，但 余弦距離 的區分度相對較弱，因為它對空間的聚集性不如歐氏距離敏感。
- 當 p 值較大，q 值較小時，Node2Vec 強調 全局結構，類似于 深度優先搜索（DFS）。在這種設置下，Node2Vec 更傾向于 捕捉較遠的、非直接連接節點的關系，從而使得正負樣本在 余弦距離 上的分布更加分散，區分度更佳。但與此同時，由于較大 p 值導致的 探索全局結構，負樣本和正樣本的 歐氏距離 變得相對較小，且整體的聚集度較高。

ps：為什么不同距離度量的樣本區分度大有不同？

如果主要關注近鄰節點，直接相連的節點關注度較高，歐氏距離更容易區分，而余弦距離 的區分度較弱，因為余弦距離對相似性度量的需求更加依賴于 整體方向，而不單單是相對距離。但是如果更傾向捕捉到節點在 全局圖結構中的角色，正負樣本的 歐氏距離 會趨于較小，因為這時節點間的連接不再僅限于直接鄰域。

別的嘗試：

鑒于圖神經網絡具備端到端訓練的能力，后嘗試采用生成式模型來學習節點的表示（embedding），GAE 與 VGAE 本質上建模的是圖數據的生成過程，因此在理論上具備較強的表達能力。
但是，查閱到文獻中普遍指出這類模型依賴于節點的屬性信息作為輸入特征。而在本實驗中，圖中僅包含節點及其連接關系，缺乏節點特征，因此只能使用全1或one-hot等虛擬特征作為替代。在這種特征缺失的情況下，模型難以從輸入中學習到有效的結構區分信息，最終導致 GAE/VGAE 的實驗表現明顯低于Node2Vec 方法。

在這里插入圖片描述