貝葉斯優化Transformer融合支持向量機多變量時間序列預測，Matlab實現

效果一覽

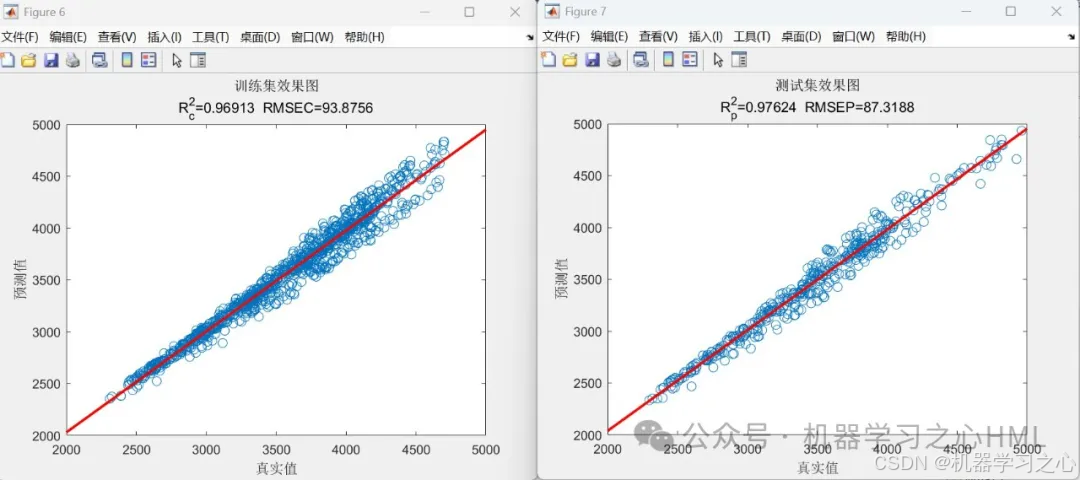
基本介紹

1.BO-Transformer+SVM多變量時間序列預測，BO-SVM/Bayes-Transformer+SVM（程序可以作為論文創新支撐，目前尚未發表）；

2.BO-SVM/Bayes-Transformer提取特征后，輸入SVM中，運行環境為Matlab2023b及以上；

3.data為數據集，輸入多個變量，輸出單個變量，考慮歷史特征的影響，main.m為主程序，運行即可,所有文件放在一個文件夾；

4.命令窗口輸出R2、MSE、RMSE、MAE、MAPE、MBE等多指標評價。

代碼功能
此代碼實現了一個結合Transformer模型和SVM的時間序列預測框架，具體功能包括：

數據預處理：導入時間序列數據，通過延時步長預測構建輸入-輸出序列對。

模型構建：使用貝葉斯優化搜索Transformer的超參數（注意力頭數、學習率、正則化系數），構建包含位置嵌入和自注意力機制的Transformer模型。

特征提取與預測：利用訓練好的Transformer提取序列特征，輸入到SVM模型中進行回歸預測。

性能評估：計算RMSE、R2、MAE、MAPE、MBE、MSE等指標，并繪制預測結果對比圖及誤差分析圖。

主要原理
時間序列建模：通過歷史數據預測，將時間序列轉換為監督學習問題。

Transformer模型：利用自注意力機制捕捉序列中的長程依賴關系，位置嵌入層編碼時間順序信息。

貝葉斯優化：在超參數空間中搜索最優組合，平衡探索與利用，提高模型性能。

SVM回歸：將Transformer提取的高維特征作為輸入，利用SVM的非線性擬合能力進行預測。

模型結構
Transformer部分：

輸入層：接收序列數據，維度為原始特征數（numChannels）。

位置嵌入層：為輸入序列添加位置編碼，增強模型對時序的感知。

自注意力層：包含兩個多頭自注意力層（頭數由貝葉斯優化確定），用于捕捉序列內部的依賴關系。

全連接層：將注意力輸出映射到目標維度（outputSize=1）。

SVM部分：

使用Transformer中間層的激活值作為特征，通過支持向量回歸（SVR）進行最終預測。

算法流程
數據準備：

劃分輸入-輸出序列對，歸一化數據。

將訓練集和測試集轉換為序列輸入格式。

超參數優化：

貝葉斯優化搜索numHeads、InitialLearnRate、L2Regularization。

模型訓練：

使用優化后的超參數訓練Transformer模型。

提取Transformer中間層特征，訓練SVM模型。

預測與評估：

對訓練集和測試集進行預測，反歸一化后計算誤差指標。

繪制預測對比圖、誤差分布圖及擬合效果圖。

應用場景
時間序列預測：適用于需利用歷史數據預測下一個點的場景，如：

股票價格預測

能源負荷預測

氣象數據預測（溫度、降水量）

工業設備故障預警

多變量序列建模：支持多特征輸入（如同時考慮溫度、濕度、風速預測未來溫度）。

小樣本優化：貝葉斯優化可在較少迭代次數下找到較優超參數，適合計算資源有限的任務。

程序設計

完整源碼私信回復貝葉斯優化Transformer融合支持向量機多變量時間序列預測，Matlab實現

%%  清空環境變量
warning off             % 關閉報警信息
close all               % 關閉開啟的圖窗
clear                   % 清空變量
clc                     % 清空命令行%%  導入數據
result = xlsread('數據集.xlsx');%%  數據分析
num_samples = length(result);  % 樣本個數
kim = 2;                       % 延時步長（前面多行歷史數據作為自變量）
zim =  1;                      % 跨zim個時間點進行預測
nim = size(result, 2) - 1;     % 原始數據的特征是數目%%  劃分數據集
for i = 1: num_samples - kim - zim + 1res(i, :) = [reshape(result(i: i + kim - 1 + zim, 1: end - 1)', 1, ...(kim + zim) * nim), result(i + kim + zim - 1, end)];
end%%  數據集分析
outdim = 1;                                  % 最后一列為輸出
num_size = 0.7;                              % 訓練集占數據集比例
num_train_s = round(num_size * num_samples); % 訓練集樣本個數
f_ = size(res, 2) - outdim;                  % 輸入特征長度%%  劃分訓練集和測試集
P_train = res(1: num_train_s, 1: f_)';
T_train = res(1: num_train_s, f_ + 1: end)';
M = size(P_train, 2);P_test = res(num_train_s + 1: end, 1: f_)';
T_test = res(num_train_s + 1: end, f_ + 1: end)';
N = size(P_test, 2);%%  數據歸一化
[p_train, ps_input] = mapminmax(P_train, -1, 1);%將訓練集和測試集的數據調整到0到1之間
p_test = mapminmax('apply', P_test, ps_input);[t_train, ps_output] = mapminmax(T_train, -1, 1);% 對測試集數據做歸一化
t_test = mapminmax('apply', T_test, ps_output);%%  數據平鋪
%   將數據平鋪成1維數據只是一種處理方式
%   也可以平鋪成2維數據，以及3維數據，需要修改對應模型結構
%   但是應該始終和輸入層數據結構保持一致
p_train =  double(reshape(p_train, f_, 1, 1, M));
p_test  =  double(reshape(p_test , f_, 1, 1, N));
t_train =  double(t_train)';
t_test  =  double(t_test )';%%  數據格式轉換
for i = 1 : MLp_train{i, 1} = p_train(:, :, 1, i);
endfor i = 1 : NLp_test{i, 1}  = p_test( :, :, 1, i);
end

參考資料

[1] https://blog.csdn.net/kjm13182345320/article/details/129215161
[2] https://blog.csdn.net/kjm13182345320/article/details/128105718