一、卷積的概念
????????卷積是一種數學運算,通常用于信號處理和圖像分析。在卷積神經網絡中,卷積操作用于提取輸入數據(如圖像)中的特征。通過將輸入數據與卷積核(濾波器)進行卷積運算,CNN能夠識別圖像中的邊緣、紋理和其他重要特征。
二、卷積核的概念
????????卷積核(或稱為濾波器)是一個小矩陣,通常比輸入數據的尺寸小。卷積核在輸入圖像上滑動(即進行卷積運算),計算在其覆蓋區域內的加權和,從而生成特征圖(feature map)。卷積核的參數通常是可以學習的,訓練過程中會自動調整以優化模型的性能。
????????卷積核其實是一個小矩陣,在定義時需要考慮以下幾方面的內容:
????????????????卷積核的個數:卷積核的個數決定了其輸出特征矩陣的通道數。
????????????????卷積核的值:卷積核的值是自定義的,根據想要提取的特征來進行設置的,后續 進行更新,就像全連接中的 一樣,只是乘積運算變成卷積運算。
????????????????卷積核的大小:常見的卷積核有1x1、3x3、5x5等,注意一般都是奇數x奇數。
三、卷積的過程
卷積過程包括以下幾個步驟:
-
選擇卷積核:定義一個大小為?K×K?的卷積核。
-
滑動卷積核:將卷積核從輸入圖像的左上角開始,向右和向下滑動,逐步覆蓋整個圖像。
-
計算加權和:在卷積核覆蓋的區域,按元素相乘并求和,生成輸出特征圖的相應位置的值。
-
重復:繼續移動卷積核,直到覆蓋完所有位置。
????????卷積的過程是將卷積核在圖像上進行滑動計算,每次滑動到一個新的位置時,卷積核 和圖像進行點對點的計算, 并將其求和得到一個新的值,然后將這個新的值加入到特征圖中,最終得到一個新的 特征圖。

????????第一次卷積就是從輸入特征矩陣的左上角開始,通過點對點的計算,就是1x0、 0x0、0x1、0x0等計算,并將其乘積的結果加起來,得到一個新的值1,這就完成第 一次卷積操作。?
????????接著卷積核就會在輸入特征矩陣上不斷的滑動卷積,先向右,到最右邊之后,就會向 下移動一格,然后從最左邊開始向右滑動。也就是說,卷積過程秉持著先左后右、先 上后下的移動規律進行卷積,直到右下角位置為止。?
????????可以通過不斷調整卷積核的大小、卷積核的值和卷積操作的步長,可以提取出不同尺 度和位置的特征。?
????????可以看到,用一條右上到左下的卷積核去和輸入特征做卷積,得到的結果 中,從右上到左下的值變的比其它地方的大。
????????根據分類算法中Softmax和交叉熵的理解,當一個地方的值變大之后,這個值會使得 整個概率分布更加偏向于這個地方, 也就是說,這個地方的概率會變得更高。
????????因此,從Softmax和交叉熵的角度來看,這 個位置的值變大是一個好的預測結果。 在交叉熵損失函數中,它衡量了模型輸出的概率分布與實際標簽的分布之間的差異。
????????具體來說,當某一類別的概率較大而實際標簽對應的類別為1時,交叉熵損失較小; 反之,如果概率較小而實際標簽對應的類別為1時,交叉熵損失較大。
????????因此,通過提高某一特定特征區域的值,模型更加關注這一特征,有助于提高對應類 別的概率得分,從而改善模型的性能。
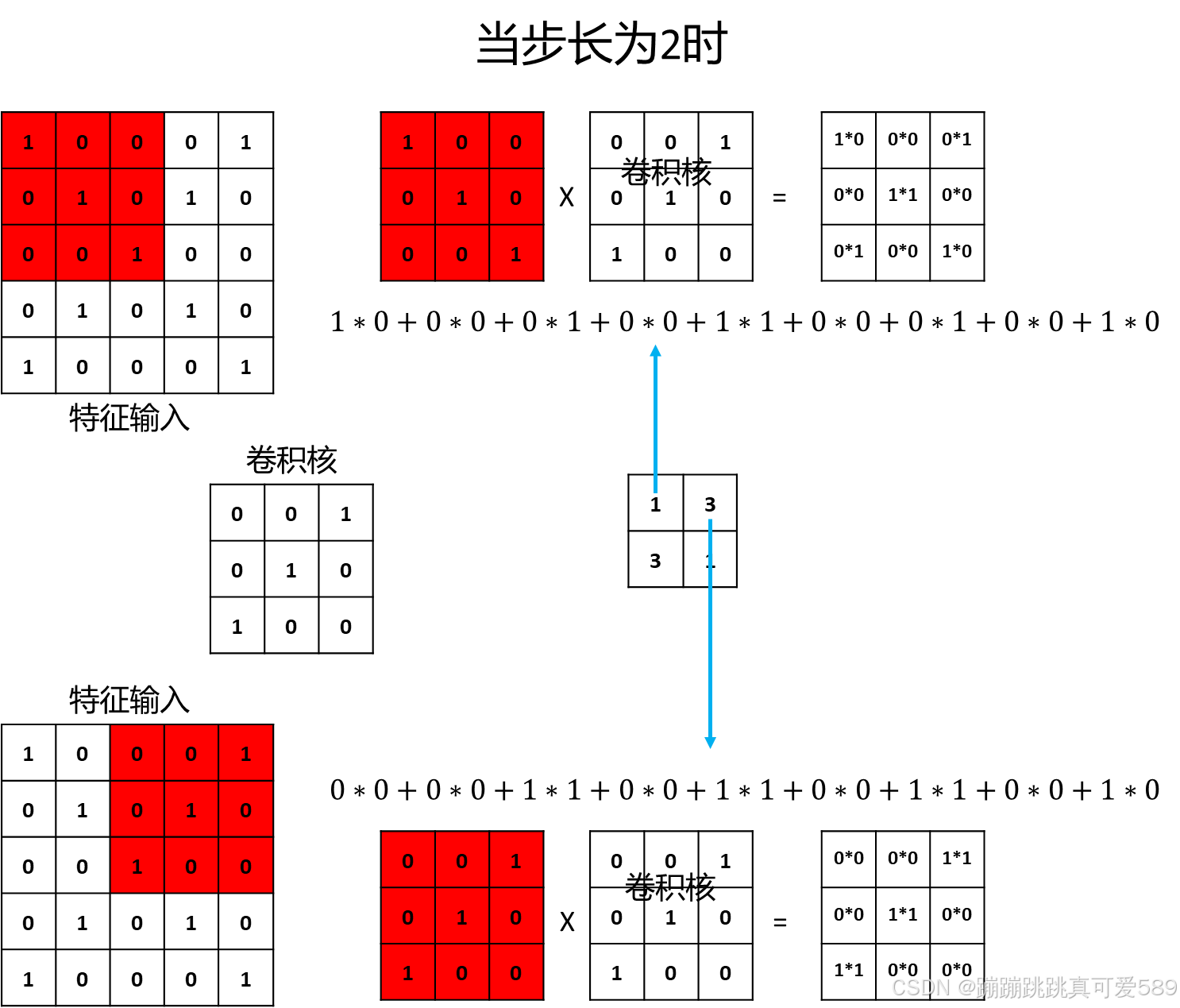
四、步長
????????步長(stride)是指卷積核在輸入數據上滑動的步幅。步長的大小影響輸出特征圖的尺寸。步長為1時,卷積核每次移動一個像素;步長為2時,卷積核每次移動兩個像素。步長的選擇對卷積層的計算量和特征圖大小有直接影響。
五、Padding
????????Padding(填充值)是指在輸入數據的邊緣添加額外的像素,以控制輸出特征圖的大小。Padding 可以幫助在卷積過程保持空間信息,尤其是當卷積核在輸入邊緣時。通常使用填充(Padding)操作來增加圖像的大小,以便在應用卷積操作時保持輸出 特征圖的大小與輸入特征圖相同或更接近。常用的 Padding 類型包括“VALID”和“SAME”。
5.1、VALID
????????VALID Padding(有效填充)意味著在進行卷積運算時,不在輸入圖像的邊緣添加任何填充值。結果是輸出特征圖的尺寸會小于輸入圖像的尺寸,因為卷積核無法覆蓋到所有輸入數據的邊緣。

5.2、SAME
????????SAME Padding(相同填充)意味著在進行卷積運算時,向輸入圖像的邊緣添加填充值,以確保輸出特征圖的尺寸與輸入圖像相同(在步長為1的情況下)。這樣可以保持特征圖的空間結構,同時又允許卷積核充分利用輸入數據。

六、?卷積核為什么總是選擇奇數大小
????????在深度學習中,卷積核的大小一般選擇奇數是為了方便處理和避免引入不必要的對稱性。
????????當卷積核的大小是奇數時,它具有唯一的一個中心像素,這個中心像素點可以作為滑 動的默認參考點,即錨點。 這使得在進行卷積操作時,卷積核可以在輸入圖像的每個像素周圍均勻地取樣。這樣 的好處是,在進行卷積操作時,可以保持對稱地處理圖像的每個位置,從而避免引入 額外的偏差和不對稱性。
????????相反,如果卷積核的大小是偶數,那么在某些位置上,中心 像素會落在兩個相鄰的像素之間,這可能導致對稱性問題。
????????此外,選擇奇數大小的卷積核還有一個重要的優點是,在進行空間卷積時,可以確保 卷積核有一個明確的中心像素,這有助于處理圖像的邊緣和邊界像素,避免模糊和信 息損失。 當然,并不是所有情況下都必須選擇奇數大小的卷積核。
????????在某些特定情況下,偶數大 小的卷積核也可以使用,并且在某些特定任務中可能表現得更好。但是在大多數情況 下,奇數大小的卷積核是一種常見且推薦的選擇,因為它可以簡化卷積操作,并有助 于保持圖像處理的對稱性和一致性。
七、設計思路
import tensorflow as tf # 輸入特征張量
# [batch_size, input_height, input_width, in_channels]
# 這里創建了一個形狀為 (1, 5, 5, 1) 的輸入張量,代表一個批次,大小為5x5的圖像,1個通道
input = tf.constant([[ [[1], [0], [0], [0], [1]], [[0], [1], [0], [1], [0]], [[0], [0], [1], [0], [0]], [[0], [1], [0], [1], [0]], [[1], [0], [0], [0], [1]]
]], dtype=tf.float32) # 卷積核張量
# [kernel_height, kernel_width, in_channels, out_channels]
# 這里創建了一個形狀為 (3, 3, 1, 1) 的卷積核,代表3x3的濾波器,1個輸入通道,1個輸出通道
wc1 = tf.constant([[ [[0]], [[0]], [[1]]], [[[0]], [[1]], [[0]]], [[[1]], [[0]], [[0]]]
], dtype=tf.float32) # 創建卷積層
# 使用 tf.nn.conv2d 進行卷積操作,strides=[1, 1, 1, 1] 表示在每個維度上移動1步,padding='SAME' 填充使輸出與輸入相同大小
conv_layer1 = tf.nn.conv2d(input, wc1, strides=[1, 1, 1, 1], padding='SAME') # 將卷積的輸出轉為 NumPy 數組
output1 = conv_layer1.numpy() # 獲取卷積層輸出特征圖的形狀
batch_size = output1.shape[0] # 批次大小
height = output1.shape[1] # 高度
width = output1.shape[2] # 寬度
channels = output1.shape[3] # 通道數 # 打印卷積后特征圖的形狀和值
print(f"卷積后的特征大小: [batch_size={batch_size}, height={height}, width={width}, channels={channels}]")
print("輸出特征圖:", output1.reshape(height, width)) # 以 (height, width) 的形狀打印輸出特征圖 














)

)

