人工智能與機器學習：Python從零實現K-Means 算法

🧠 向所有學習者致敬！

“學習不是裝滿一桶水，而是點燃一把火。” —— 葉芝

我的博客主頁： https://lizheng.blog.csdn.net

🌐 歡迎點擊加入AI人工智能社區！

🚀 讓我們一起努力，共創AI未來！ 🚀

K-Means 可是我超喜歡的機器學習算法呢，因為它能幫我們發現數據里那些隱藏起來的模式呢。要是用得好的話，它能把你數據里的分組或者聚類情況展示得明明白白的，那可都是因為它背后那些嚴謹的數學原理呢。這在現實生活中可有不少厲害的應用呢。

比如說呀，要是你負責分析一個電商網站的點擊流數據呢，你就可以用 K-Means 把顧客按照他們點擊的內容、加入購物車的東西，還有購買的東西來分成不同的群組呢。這就能幫你搞出一套個性化策略呢，根據顧客所在的群組，把網站體驗調整得更符合他們的需求呢。好啦，現在咱們就來好好研究一下這個算法吧！

K-Means 算法

首先得跟大家說說，K-Means 算法是一種無監督機器學習算法哦。無監督機器學習模型的關鍵特點就是，咱們的數據里沒有目標值或者標簽呢。換句話說呢，咱們不是要預測啥東西，而是想給數據貼上標簽呢。在 K-Means 算法里呀，咱們的目標就是把數據分成不同的群組或者聚類呢。那怎么做到呢？首先呢，用戶可以指定要把數據分成多少個聚類呢。我為啥說“可以指定”呢，其實呢，這還是得講究一些最佳實踐呢。要是聚類數太少呢，可能會錯過一些對你用例很有價值的信息呢；要是聚類數太多呢，又會變得冗余啦。在給數據點分配聚類的時候呢，每個數據點都會被分配到離它最近的那個聚類呢。現在呢，還有更多細節要講，咱們接著往下看吧。

關鍵概念：歐幾里得距離

None

回想一下你以前上過的數學課吧。你可能還記得有個叫勾股定理的東西呢：

$a^{2} + b^{2} = c^{2}$

咱們用這個公式來計算直角三角形的斜邊長度呢（我以前叫它“長邊”）。要是想得到 c 的確切數值呢，就得對 a2 + b2 開平方根呢。你可能不知道呢，其實你已經學會了怎么計算坐標平面上兩個點之間的距離啦！這其實也是線性代數里的一個概念，叫 L2 范數呢。假設你有一個二維坐標平面，x 是水平軸，y 是垂直軸。給定兩個點，(x1,y1) 和 (x2,y2)，咱們就可以用這個公式來計算它們之間的歐幾里得距離呢：

None

咱們也可以在超過兩個維度的情況下計算歐幾里得距離呢。比如說，這是計算三維空間中兩個點之間距離的公式呢：

None

那這和 K-Means 有啥關系呢？咱們接著往下看下一節就知道啦。

質心：初始化、迭代、收斂

先來舉個 K-Means 的簡單例子吧。下面這張圖呢，是我隨便編的一個有兩個維度的虛構數據集呢。要是你把單獨的數據點都畫出來呢，看起來大概就是這樣的。你可能覺得，用不著 K-Means 也能把這些數據分成不同的聚類呢，因為它們分組的方式看起來還挺明顯的呢。不過呢，我還是會給大家演示一下它是怎么工作的呢。

None

圖片來源：作者提供

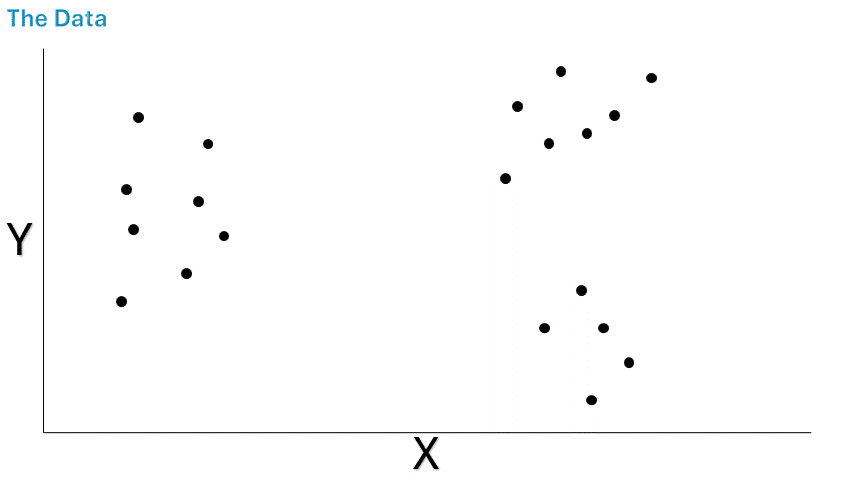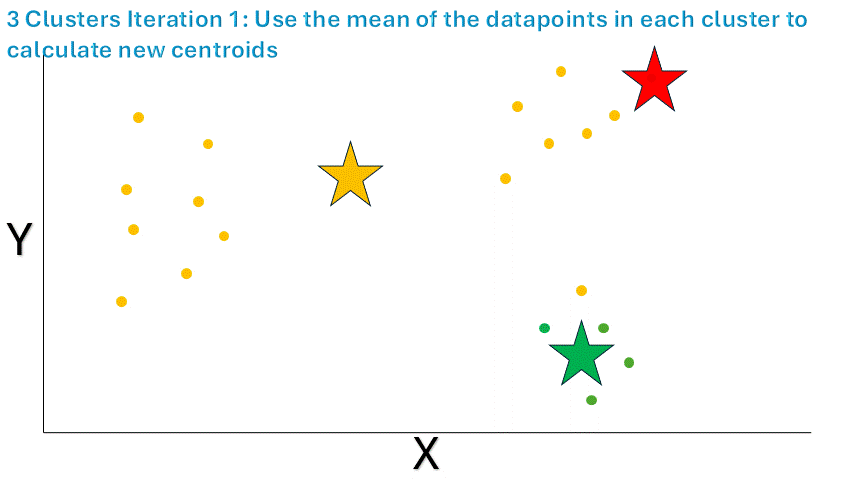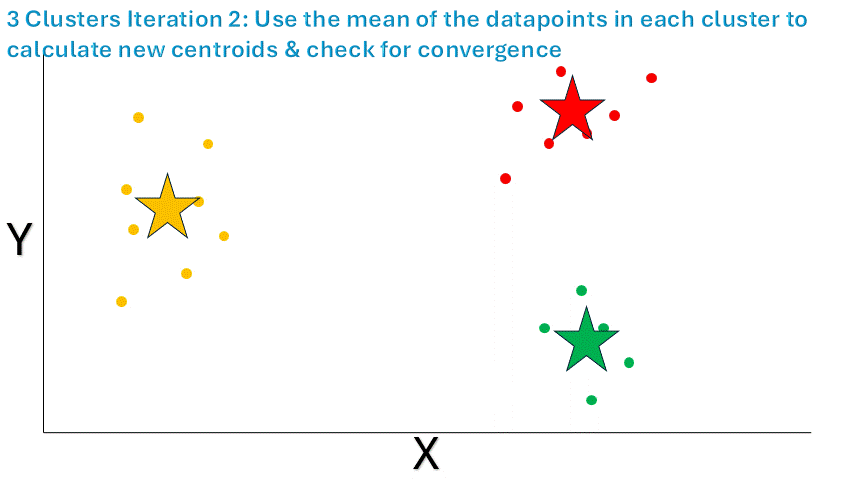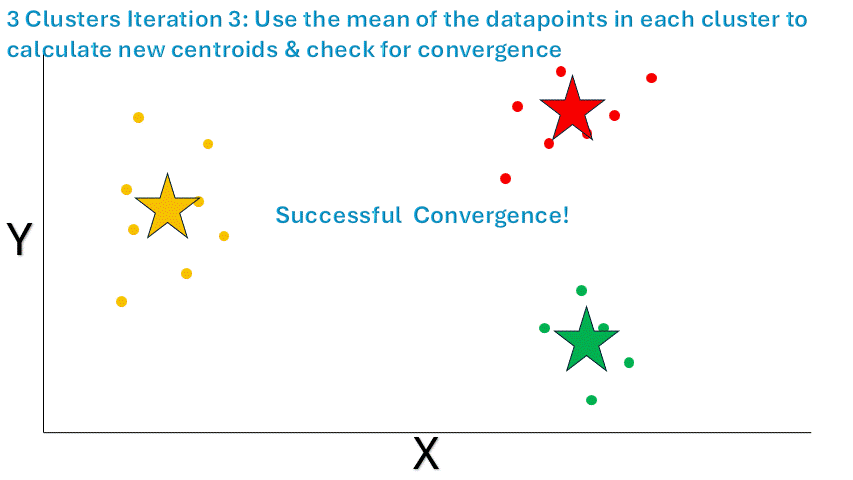
就像我之前說的呢，咱們可以指定要把數據分成多少個聚類呢。在這個例子里呢，咱們就把它分成 3 個聚類吧。咱們先隨機生成三個坐標，當作初始的質心來開始這個過程呢。質心呢，就是用來代表一個聚類中心的坐標呢。咱們用星形來標記這些隨機生成的質心吧：

None

圖片來源：作者提供

接下來呢，咱們要根據歐幾里得距離來給數據點分配質心啦。換句話說呢，就是把每個數據點分配給離它最近的那個質心呢。你是不是已經看出來啦，歐幾里得距離在 K-Means 里可起著關鍵作用呢！

None

圖片來源：作者提供

完成初始化步驟之后呢，咱們要計算每個聚類里分配到的點的平均值呢，然后把得到的坐標當作新的質心呢。比如說呢，在這個例子里，有一個聚類里分配到了一組點呢，咱們就取這些點的 x 和 y 坐標的平均值呢，然后用得到的坐標作為新的質心或者聚類中心呢。結果大概會是這樣的（注意那個“紅色”聚類的質心正好就在一個數據點上，因為那個聚類里只有一個數據點呢）：

None

圖片來源：作者提供

這些聚類看起來好像不太合理呢，對吧？別擔心，咱們還沒做完呢。咱們再重復一次給聚類分配數據點的過程吧。首先呢，咱們隨機初始化三個質心：

None

圖片來源：作者提供

然后呢，根據歐幾里得距離把數據點分配給最近的質心呢。

None

最后呢，咱們計算每個聚類里數據點的平均坐標呢，然后把得到的坐標當作新的質心呢。

None

圖片來源：作者提供

用肉眼看呢，K-Means 算法好像已經把這個數據集分成三個不同的聚類啦。不過呢，它自己還不知道已經找到了最優解呢。所以呢，咱們還得重復同樣的過程，不過這次咱們要檢查新的聚類和之前的聚類是不是有很大區別呢。關于這個概念，咱們很快就會展開說呢。先來看看收斂是怎么實現的吧。

你肯定已經知道流程啦，咱們先隨機生成質心：

None

圖片來源：作者提供

根據歐幾里得距離把數據點分配給最近的質心：

None

最后呢，咱們計算每個聚類里數據點的平均坐標呢，然后把得到的坐標當作新的質心呢。同時呢，咱們還要檢查新的質心和之前的質心之間的距離是不是低于咱們設定的閾值呢。在這個例子里呢，距離是 0，肯定已經滿足咱們的標準啦，算法已經收斂啦：

None

尋找最佳聚類數量

給定 k 個聚類數量呢，咱們現在知道怎么把數據分成 k 個聚類啦。不過呢，這還是留下了一個問題：最佳的聚類數量 k 到底是多少呢？

咱們可以用一些方法來解決這個問題呢，在咱們要搭建的 KMeans 對象里呢，咱們會找出來哪個聚類數量能得到最高的輪廓系數呢：

None

圖片來源：作者提供

a 是每個聚類里數據點和聚類質心之間的平均距離呢，而 b 是每個聚類質心和最近的相鄰聚類質心之間的平均距離呢。更實際地說呢，輪廓系數越高呢，就意味著聚類里的點越能很好地定義到自己的聚類里呢，而且各個聚類之間也分得更清楚呢。

KMeans 類

咱們已經了解了 KMeans 算法的所有必要概念啦！現在呢，該開始搭建咱們的對象啦。咱們先從創建初始化函數開始吧。就像你看到的呢，咱們要用到的庫只有 numpy、pandas、tqdm（用來顯示進度條）和 scikit-learn 里的 silhouette_score 對象呢（別擔心，這是咱們唯一從 sklearn 里用到的東西，這樣咱們就能真正從頭搭建這個算法啦）。咱們來聊聊這些屬性吧。

import numpy as np
import pandas as pd
from sklearn.metrics import silhouette_score
from tqdm import tqdmclass DIYKMeans:def __init__(self, max_k=10, max_iters=100, tol=1e-4, random_state=None):self.max_k = max_kself.max_iters = max_itersself.tol = tolself.random_state = random_stateself.k = Noneself.centroids = Noneself.labels_ = Noneself.X_scaled = Noneself.feature_means = Noneself.feature_stds = Noneself.stable_iterations = 0

max_k: 嘗試擬合模型時聚類數量的上限。
max_iters: 擬合模型時隨機初始化質心的最大嘗試次數。
tol: 計算新舊質心距離時的容差閾值。
random_state: 隨機狀態值，方便復現結果。
k, centroids, labels_: 找到基于輪廓系數的最佳 k 后，這些屬性就會被賦值。k 是最佳聚類數量，centroids 是最佳 k 對應的質心坐標，labels_ 是每個數據點的聚類標簽。
X_scaled, feature_means, feature_stds: 數據的標準化值，以及對應的均值和標準差。
stable_iterations: 用來記錄在容差范圍內的迭代次數，默認情況下，這個對象會在連續三次迭代滿足容差條件后認為算法已經收斂。

質心操作與標準化

接下來的這些方法呢，會涉及到 K-Means 算法的基本操作呢。這些內容應該都很熟悉啦，畢竟咱們之前已經講過啦。注意咱們還加了一個標準化數據的方法呢。為啥這個很重要呢？因為咱們的算法要求數據得在同一尺度上呢，不然那些取值范圍大的特征就會讓算法偏向它們呢。比如說呢，假設咱們想根據臥室數量、浴室數量和價格來聚類房屋數據呢。臥室和浴室的數量平均可能在 1 到 5 之間呢，但價格可能會達到幾十萬呢。要是不標準化的話，計算距離的時候大部分影響都會來自價格特征呢。所以呢，咱們必須標準化或者歸一化數據。在這個例子里呢，咱們的標準化方法用的是均值標準化呢。最后呢，咱們看看收斂方法是怎么實現的吧。我發現這個算法的一個缺點呢，就是確認算法收斂的時候，只要新舊質心之間的距離在容差范圍內變化一次就行啦。為了確保更穩定的收斂呢，咱們的方法會在連續三次迭代滿足容差條件后才認為算法已經收斂啦。

standardize_data: 把每個特征都標準化到同一尺度上。
initialize_centroids: 給定數據集的特征數量和 k，它會隨機生成 k 個維度和數據集特征數量相同的質心。
compute_distances: 利用 numpy 自帶的線性代數庫呢，這個函數用來計算歐幾里得距離呢，也就是兩個坐標之間形成的向量的長度。
assign_clusters: 給定一個數據點和質心，返回最小距離對應的索引。
compute_new_centroids: 把每個質心對應的點取出來呢，計算每個特征的均值呢，然后返回新的質心坐標。
has_converged: 給定一個容差值呢，檢查新質心和舊質心之間的差異是不是在容差范圍內呢。這個方法會檢查連續三次迭代是不是都滿足容差條件呢。要是滿足的話呢，就停止操作，認為算法已經收斂啦。

def standardize_data(self, X):self.feature_means = np.mean(X, axis=0)self.feature_stds = np.std(X, axis=0)self.feature_stds[self.feature_stds == 0] = 1return (X - self.feature_means) / self.feature_stdsdef initialize_centroids(self, X, k):np.random.seed(self.random_state)return X[np.random.choice(X.shape[0], k, replace=False)]def compute_distances(self, X, centroids):return np.linalg.norm(X[:, np.newaxis] - centroids, axis=2)def assign_clusters(self, distances):return np.argmin(distances, axis=1)def compute_new_centroids(self, X, labels, k):return np.array([X[labels == i].mean(axis=0) for i in range(k)])def has_converged(self, old_centroids, new_centroids, stable_threshold=3):if np.linalg.norm(new_centroids - old_centroids) < self.tol:self.stable_iterations += 1else:self.stable_iterations = 0return self.stable_iterations >= stable_threshold

擬合方法

這個方法就是把所有東西都整合到一起啦。根據咱們的 max_k 屬性呢，咱們會嘗試這個范圍內的所有 k 值呢。對于每個 k 呢，咱們會運行迭代過程呢，隨機初始化質心，給點分配聚類，然后重新計算質心，直到收斂為止呢。在這個過程中呢，咱們還會計算輪廓系數呢。哪個 k 值能得到最高的輪廓系數呢，咱們就會把數據集分成那個數量的聚類呢。從那以后呢，咱們的 k、centroids 和 labels_ 屬性就會被賦上最佳數據啦。

def fit(self, X):X = np.array(X)X = self.standardize_data(X)self.X_scaled = Xbest_k = Nonebest_score = -1best_labels = Nonebest_centroids = Noneprint("Fitting KMeans across different k values:")for k in tqdm(range(2, self.max_k + 1), desc="Searching for optimal k"):centroids = self.initialize_centroids(X, k)self.stable_iterations = 0for _ in range(self.max_iters):distances = self.compute_distances(X, centroids)labels = self.assign_clusters(distances)new_centroids = self.compute_new_centroids(X, labels, k)if self.has_converged(centroids, new_centroids):breakcentroids = new_centroidsscore = silhouette_score(X, labels)if score > best_score:best_k = kbest_score = scorebest_labels = labelsbest_centroids = centroidsself.k = best_kself.centroids = best_centroidsself.labels_ = best_labels

用信用卡數據來測試

現在呢，咱們來用 Kaggle 上的一個信用卡數據集來測試一下咱們自己搭建的 KMeans 對象吧。

假設你在一個信用卡公司當數據科學家呢，領導讓你找出顧客的分群呢。以前呢，業務團隊是根據顧客通常購買的東西和平均月余額來分群的呢。現在呢，領導想擴大這個邏輯，但又不知道怎么搞出一個能擴展的方案呢。這時候呢，咱們自己搭建的 KMeans 對象就派上用場啦。

咱們先從導入數據開始吧。

data = pd.read_csv('CC GENERAL.csv')

這個數據集里有很多特征呢，不過呢，咱們先別一下子把業務團隊嚇著，所以咱們只保留以下這幾列呢。這些定義都是從我下載數據的 Kaggle 頁面上直接拿過來的哦：

BALANCE_FREQUENCY: 余額更新的頻率，是一個 0 到 1 之間的分數（1 = 經常更新，0 = 不經常更新）

PURCHASES_FREQUENCY: 購買的頻率，是一個 0 到 1 之間的分數（1 = 經常購買，0 = 不經常購買）

CREDIT_LIMIT: 用戶的信用卡額度

PAYMENTS: 用戶支付的金額

PRCFULLPAYMENT: 用戶支付全額的比例

TENURE: 用戶使用信用卡服務的年限

cols_to_keep = ['BALANCE_FREQUENCY','PURCHASES_FREQUENCY','CREDIT_LIMIT','PAYMENTS','PRC_FULL_PAYMENT','TENURE']
data_for_kmeans = data[cols_to_keep]
data_for_kmeans = data_for_kmeans.dropna()

咱們先來做點簡單的探索性分析呢，看看這些特征的一些基本情況吧。以下是這個數據集的一些關鍵事實呢。

咱們看到的是大約 8600 個有完整數據的顧客樣本呢。
購買頻率高和購買頻率低的顧客各占一半呢。
大多數顧客的信用卡額度都在 6500 美元以下呢。
大多數顧客支付的金額在 2000 美元以下呢，但最高支付金額可以達到 50000 美元呢。
大多數顧客支付的金額只占他們應付款項的 15% 左右呢。
大多數顧客使用信用卡服務的年限是 12 年，而且變化不大呢。

data_for_kmeans.describe()

None

圖片來源：作者提供

用咱們自己搭建的 KMeans 模型來擬合

現在咱們已經對數據有了更好的了解啦，那就開始用咱們的模型來擬合它吧。

km = DIYKMeans(max_k=20)
km.fit(X=data_for_kmeans)

None

圖片來源：作者提供

print('最佳聚類數量：',km.k)

None

理解聚類結果

太棒啦！咱們自己搭建的 KMeans 對象把數據集分成了 7 個聚類呢。咱們的工作還遠遠沒有結束呢。現在咱們已經從數學上把顧客分成了不同的群組啦，那咱們就來好好探索一下每個群組里的關鍵模式吧。為了做到這一點呢，我搭建了一個自定義函數呢，它可以輸出每個群組的數量呢，還能顯示每個特征的平均值呢，還會生成一個熱力圖呢，這樣就能很方便地比較和對比啦。我在咱們的對象的 labels_ 屬性基礎上給數據集加了一個“Cluster”列呢。以下是我發現的關鍵模式呢：

除了第 3 個聚類以外，每個聚類都包含使用信用卡服務年限接近 12 年的顧客呢。
第 2 個聚類是唯一一個購買頻率高而且支付比例也高的群組呢，它的信用卡額度只是略高于平均水平呢。
第 0 個、第 4 個和第 5 個聚類支付比例都非常低呢；不過呢，第 4 個聚類是這三個聚類里購買頻率最低的呢。
第 6 個聚類是高消費群組呢，信用卡額度最高，支付金額也最大呢。
第 5 個聚類和第 6 個聚類在消費方面很相似呢，不過呢，支付金額要低得多呢。

根據這些模式呢，咱們能實施哪些實用的策略或者方法呢？記得哦，信用卡公司是通過收取消費者的支付手續費和利息來賺錢的呢。所以呢，公司可能希望顧客不要一次性把賬單都還清呢，這樣公司就能賺取利息啦；不過呢，要是顧客欠款太多呢，公司又收不到全額還款啦。所以呢，我有以下幾個想法：

讓第 5 個聚類的顧客支付比例接近第 6 個聚類呢。
研究一下給第 2 個聚類的顧客提高信用卡額度呢，因為他們大多數都能按時還款呢。
研究一下給第 0 個、第 4 個和第 5 個聚類的顧客降低信用卡額度呢，直到他們的支付比例提高呢。

data_for_kmeans['Cluster'] = km.labels_def summarize_by_cluster_with_heatmap(df, cluster_col='Cluster'):if cluster_col not in df.columns:raise ValueError(f"列 '{cluster_col}' 在 DataFrame 中找不到哦。")value_cols = [col for col in df.select_dtypes(include='number').columns if col != cluster_col]if not value_cols:raise ValueError("除了聚類列以外，沒有數值型列可以進行總結呢。")grouped = df.groupby(cluster_col)means = grouped[value_cols].mean().round(2).add_suffix('_mean')counts = grouped.size().to_frame('count')summary = pd.concat([counts, means], axis=1).reset_index()return summary.style.background_gradient(cmap='YlGnBu', subset=summary.columns[1:]).format("{:.2f}")summarize_by_cluster_with_heatmap(df=data_for_kmeans)