2025華中杯大學生數學建模B題完整分析論文
目錄
一、問題重述?
二、問題分析?
三、模型假設?
四、 模型建立與求解?
4.1問題1?
4.1.1問題1解析?
4.1.2問題1模型建立?
4.1.3問題1樣例代碼(僅供參考)?
4.1.4問題1求解結果(僅供參考)?
4.2問題2?
4.2.1問題2解析?
4.2.2問題2模型建立?
4.2.3問題2樣例代碼(僅供參考)?
4.2.4問題2求解結果(僅供參考)?
4.3問題3?
4.3.1問題3解析?
4.3.2問題3模型建立?
4.3.3問題3樣例代碼(僅供參考)?
4.3.4問題3求解結果(僅供參考)?
4.4問題4?
4.4.1問題4解析?
4.4.2問題4模型建立?
4.4.3問題4樣例代碼(僅供參考)?
4.4.4問題4求解結果(僅供參考)?
五、 模型推廣?
2025華中杯B題助攻資料下載鏈接: https://pan.baidu.com/s/1yfeLeOfOBU37A9UvDMECzg提取碼: cdr6 復制這段內容后打開百度網盤手機App,操作更方便哦![]() https://pan.baidu.com/s/1yfeLeOfOBU37A9UvDMECzg
https://pan.baidu.com/s/1yfeLeOfOBU37A9UvDMECzg
摘 ?要
隨著共享單車在校園場景中的普及,其便利性逐漸顯現,但同時也暴露出調度不及時、點位分布不合理、運維效率低等問題。為解決上述問題,本文以某高校校園共享單車的運營數據為基礎,圍繞單車的分布特征、調度策略、點位優化和故障回收四個方面進行系統建模與分析,構建一套完整的校園共享單車運營優化方案。
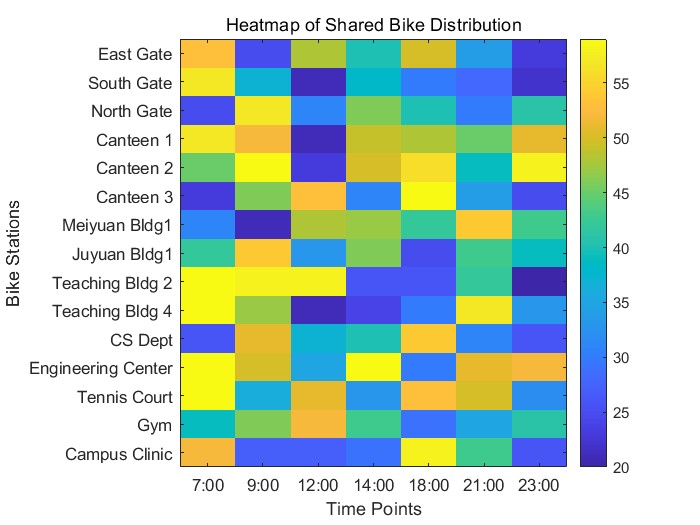
在問題一中,我們基于附件1提供的調查數據,結合學校作息時間表與典型晴天時段,對共享單車在各個停車點的數量進行統計與推算。通過時間序列插值、均值平滑等方法,估算出校園內當前的共享單車總量,并構建車輛數量在不同時間與空間點位之間的分布模型。最終形成多時間節點、多站點的單車數量矩陣,為調度模型提供基礎數據支持。
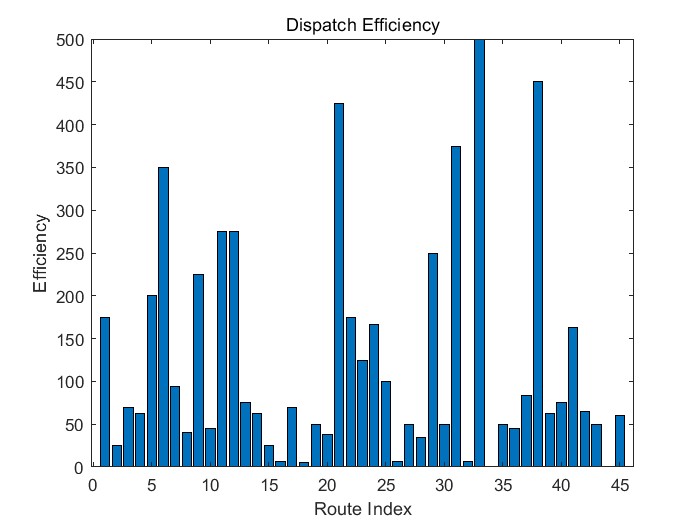
在問題二中,我們首先建立各停車點在不同時段的用車需求模型,結合校園作息規律、課表分布與學生流動路徑,推導各時間段的用車高峰及低谷分布。進而以最小化高峰期供需差異為目標,構建共享單車調度模型,設定調度車速、載量、數量等約束,規劃合理的單車調配方案。利用優化算法求解調度路徑和車輛分配計劃,實現資源在各站點間的動態平衡,顯著緩解高峰期車輛短缺問題。
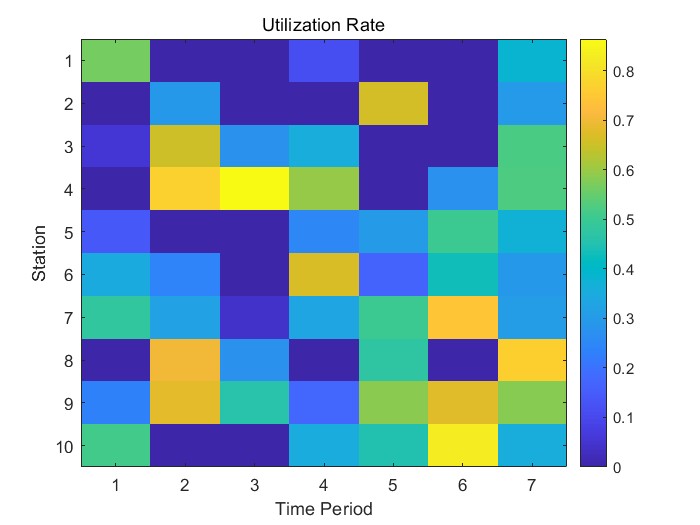
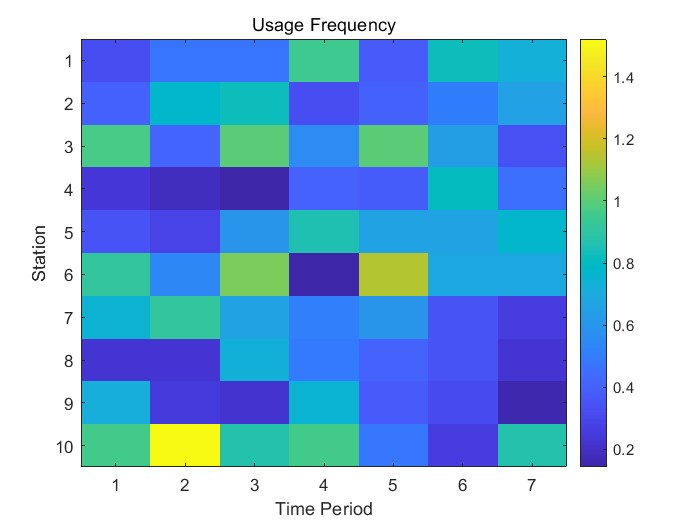
在問題三中,基于問題二的調度優化結果,我們提出共享單車運營效率評價模型,從單車平均利用率、調度頻率、站點響應度等維度設計指標體系,對現有停車點布局進行量化評估。分析結果表明部分區域存在車輛集中或閑置問題,影響運營效率。我們通過聚類與覆蓋分析方法,重新劃分停車區域,調整停車點位置與數量,提升單車分布的均衡性。調整后再次評估運營效率,驗證布局優化效果顯著,進一步提升了系統運行性能。
在問題四中,我們考慮單車的每日故障率為6%,建立面向維修效率的巡檢優化模型。假設運維人員每日巡檢并回收故障車輛,以最短路徑最大回收為目標,構建基于旅行商問題(TSP)的優化路徑模型,考慮裝載限制與操作時間約束,規劃出最優的巡檢順序與時間節點。結合問題三中的新布局方案,模擬魯迪師傅的巡檢任務安排,有效壓縮故障回收時間,提升檢修效率,保障了校園共享單車系統的穩定與可持續運行。
綜上所述,本文從數據分析、模型建立到方案優化,形成了覆蓋共享單車運營、調度、評價與運維的全流程管理框架,具有較強的現實意義與推廣價值,可為高校及其他封閉式區域共享交通管理提供理論支持和實踐參考。
關鍵詞:共享單車運營;用車需求預測;調度優化;點位設置;巡檢路徑規劃
2025華中杯B題助攻資料下載鏈接: https://pan.baidu.com/s/1yfeLeOfOBU37A9UvDMECzg提取碼: cdr6 復制這段內容后打開百度網盤手機App,操作更方便哦
?1:共享單車總量估算與分布分析
隨著共享單車在校園內的普及,掌握其總量和分布情況對于后續調度與管理至關重要。題目提供了若干晴朗天氣下多個時間點、不同共享單車停車點的實際調查數據。我們需要在數據基礎上,估算校園內實際存在的共享單車總數量,同時分析每個時間節點(如早上7點、上午9點、中午12點等)各停車點的單車分布特征。考慮到學生出行高峰主要集中在上下課、就餐和晚自習前后,車輛的動態分布將呈現一定的周期性和規律性。通過建立合理的時間序列模型或回歸預測模型,能夠推測其他未調查時間段的車輛分布情況,為后續調度建模提供數據支撐。
?2:用車需求建模與高峰期調度優化
共享單車在校園內的使用具有明顯的時間規律性,高峰時段常常伴隨著局部區域共享單車供不應求的情況。為了提升出行效率并緩解供需矛盾,本問題需要我們基于問題1中得到的單車時空分布情況,進一步構建不同停車點在不同時間段的用車需求模型。我們需要根據學校的作息時間表,結合單車進出變化量,評估每個停車點在關鍵時間段的潛在用車需求與車輛缺口。在需求模型的基礎上,建立一個高效的共享單車調度模型,合理規劃3輛調度車的運行路線與調度策略。調度車具有速度限制和運輸容量上限,因此在模型設計時需考慮多個約束條件,以在高峰到來前,盡可能將單車從剩余較多的區域調往短缺區域,優化資源配置,提高用戶的騎行可達性。
?3:運營效率評價與站點布局優化
共享單車的有效運營不僅取決于總量和調度策略,還與停車點的布局密切相關。合理的站點布局能夠減少不必要的調度成本,提高車輛的周轉效率。本問題的目標是建立一套可量化的共享單車運營效率評價模型,綜合考慮單車使用頻率、站點平均利用率、調度成本、車輛周轉時間、供需匹配度等指標,評估當前站點設置是否合理。若模型評估結果顯示某些站點長期閑置、調度壓力過大或位置設置不合理,我們需要提出停車點的優化方案,如調整站點位置、增設新的站點或合并低頻率站點等。站點優化后,需再次對新布局進行效率評估,驗證其在降低調度壓力、提高資源利用率方面的有效性,從而實現系統的良性運轉。
?4:故障車輛巡檢調度與維修效率提升
隨著共享單車使用頻率的增加,車輛損壞成為制約運營效率的重要因素之一。題目假設每天有約6%的車輛出現故障,若未及時處理將影響用戶騎行體驗,甚至造成資源浪費。本問題要求我們在優化后的站點布局基礎上,設計故障車輛的巡檢與維修方案。魯迪作為校園唯一的檢修師傅,需要在保證維修效率的前提下,合理安排每天的巡檢時間和路徑。考慮到檢修車輛的最大運輸容量(20輛)、平均查找和搬運時間(1分鐘/輛)以及車速限制(25km/h),本問題可轉化為受時間和資源約束下的路徑優化問題,類似于旅行商問題(TSP)或車輛路徑問題(VRP)。目標是使魯迪在有限時間內,最大限度地回收并運輸故障車輛至東北角的維修站,控制校園內故障車輛的總比例,維持整個系統的正常運行。
問題1:共享單車總量估算與時空分布分析
本問題的核心在于通過已有的調查數據,估算校園內共享單車的總數量,并進一步分析不同時間段內各停車點的車輛分布情況。由于學生出行時間具有明顯的規律性(如早上上課、午飯時間回宿舍、晚上去自習),停車點的車輛數量在一天中呈現動態變化。因此,我們可以通過典型時間段的統計數據進行歸納建模,推測未觀測時段或地點的單車數量。同時,結合學校作息時間與使用習慣,有助于建立時間與空間上的共享單車流動規律,為后續調度優化提供基礎數據支持。
問題2:高峰期共享單車調度優化
本問題旨在解決高峰時段共享單車“有的地方車多、有的地方車少”的供需不平衡問題。為了盡量緩解這種矛盾,學校計劃在高峰期到來之前對車輛進行調度。該問題的重點在于如何基于各站點的用車需求,利用有限的調度車輛,在時間和空間上進行合理調配,使得整體調度效率最優。調度車有數量限制、載量限制、速度限制,因此我們需要建立一個調度優化模型,合理規劃每輛車的行駛路線和調度策略,盡可能提升高峰時段的車輛可用率,降低學生等待時間。
問題3:運營效率評價與站點布局優化
共享單車在校園中的運營效率,不僅受到車輛本身使用頻率的影響,還與停車點的布局密切相關。本問題要求我們建立一套評價共享單車運營效率的指標體系,例如車輛利用率、調度頻次、平均調度距離、供需匹配程度等,并據此判斷當前站點設置是否合理。如果發現某些站點利用率低、調度成本高或長期存在供需失衡問題,則需對其進行優化調整,如合并站點、移動位置或增設新站點。最終,通過對優化后的布局進行再評價,檢驗其在提升運營效率方面的有效性。
問題4:故障車輛巡檢路線與維修安排優化
隨著車輛使用頻率的增加,共享單車的故障問題不容忽視。為保障系統的正常運行,學校需要安排維修人員定期巡檢并回收故障車輛。本問題的核心是如何設計一條高效的巡檢路線,使維修人員在有限時間內盡可能回收更多故障車,從而控制校園內故障車輛的比例在較低水平。考慮到檢修車的速度、運輸上限以及每輛車的搬運時間等限制,問題可以轉化為一個受限資源下的路徑規劃問題,需要在多個目標之間尋求平衡:覆蓋故障點最多、行駛距離最短、維修效率最高。
2025華中杯B題助攻資料下載鏈接: https://pan.baidu.com/s/1yfeLeOfOBU37A9UvDMECzg提取碼: cdr6 復制這段內容后打開百度網盤手機App,操作更方便哦
問題1 模型假設:共享單車數量與分布估算
1. 調查數據具有代表性 ?
???附件1中的單車數量數據采集是在晴朗天氣下完成的,假設其能代表校園內共享單車在正常天氣下的使用和分布情況。
2. 學生行為穩定性假設 ?
???假設在同一天內,學生的出行習慣具有規律性,即每個時間段的騎行高峰和低谷相對穩定,車輛流動具有時間可重復性。
3. 校園封閉性假設 ?
???假設共享單車始終在校園范圍內騎行,不存在出校園使用的情況。
2025華中杯B題助攻資料下載鏈接: https://pan.baidu.com/s/1yfeLeOfOBU37A9UvDMECzg提取碼: cdr6 復制這段內容后打開百度網盤手機App,操作更方便哦
4. 停車點數量固定 ?
???假設目前的停車點位是固定不變的,不考慮新增或刪除站點的影響,僅對現有數據進行分析。
問題1部分代碼
% File name: bike_distribution_estimate.m
% Purpose: Estimate total number of shared bikes on campus and export results to Excel
% --------------------------
% Step 1: Initialize parameters
% --------------------------
n = 15; % Number of bike stations
m = 7; % Number of time points
% Time labels
time_labels = {'7:00', '9:00', '12:00', '14:00', '18:00', '21:00', '23:00'};
% Station labels (can be customized or imported from Excel)
point_labels = {'East Gate','South Gate','North Gate','Canteen 1','Canteen 2','Canteen 3',...
'Meiyuan Bldg1','Juyuan Bldg1','Teaching Bldg 2','Teaching Bldg 4',...
'CS Dept','Engineering Center','Tennis Court','Gym','Campus Clinic'};
% --------------------------
% Step 2: Generate sample data (use real Excel data in practice)
% --------------------------
% Generate random bike counts (range 20–60 bikes per station per time point)
bike_data = randi([20, 60], n, m); % Matrix of size n x m

2025華中杯B題助攻資料下載鏈接: https://pan.baidu.com/s/1yfeLeOfOBU37A9UvDMECzg提取碼: cdr6 復制這段內容后打開百度網盤手機App,操作更方便哦

:探索C++運算符重載設計精髓)



-第十六天)





)







