


算法系列六:快速排序
一、快速排序的遞歸探尋
1.思路
2.書寫
3.搭建
3.1設計過掉不符情況(在最底層時)
3.2查驗能實現基礎結果(在最底層往上點時)
3.3跳轉結果繼續往上回搭
4.實質
二、快速排序里的基準排序
1.雙路雙向交換鋪(Hoare法)
1.1原理
1.2實現
1.2.1>=
1.2.2先右再左
2.雙路雙向覆蓋鋪(挖坑法)
2.1原理
2.2實現
3.雙路單向交換鋪(前后指針法)
3.1原理
3.2實現
三、快速排序的復雜度
1.時間復雜度
1.1完全順序逆序
1.1.1結構影響
1.1.2時間
1.2完全二叉樹序
1.2.1結構影響
1.2.2時間
2.空間復雜度
3.優化
3.1三數取中
3.2插入排序
3.2.1棧溢出原因
3.2.2利與弊
一、快速排序的遞歸探尋
1.思路
左斷開結果與右斷開結果加上突兀根如何實現上一層的結果:
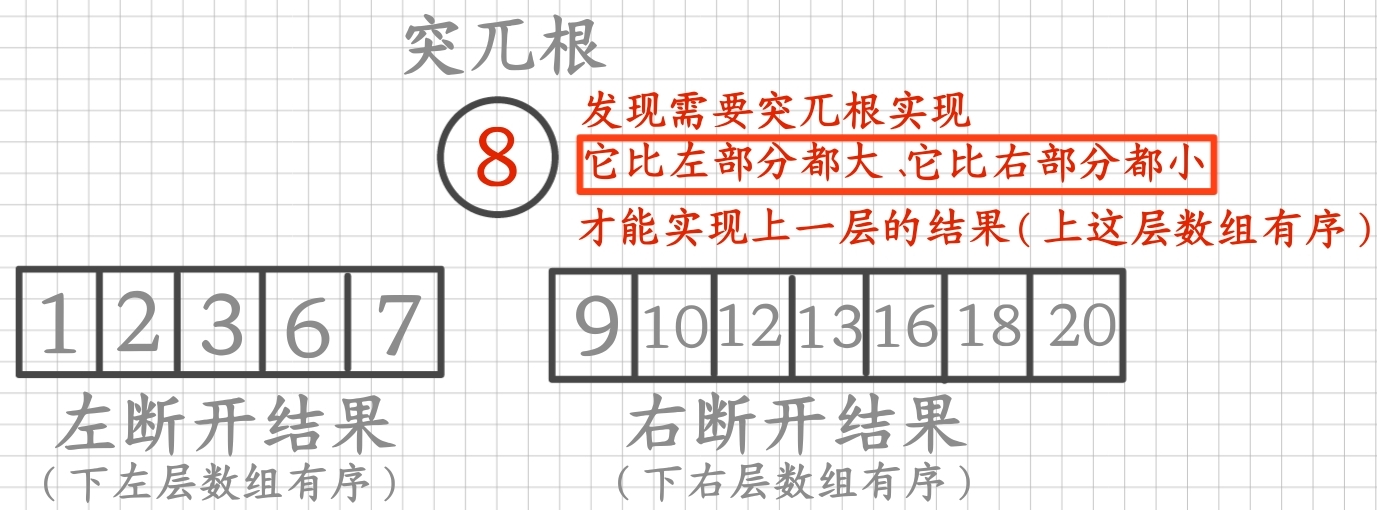
左斷開有序+右斷開有序加突兀根實現它比左部分都大、它比右部分都小就可以實現上一層的有序
2.書寫
書寫時是突兀根先實現再遞歸實現左右斷開結果:
書寫時反著來先實現突兀根一個節點左邊都比都比它小、右邊都比它大,再用遞歸實現它斷開的左右有序結果
3.搭建
突兀根從底層向上的回搭搭建二叉樹:
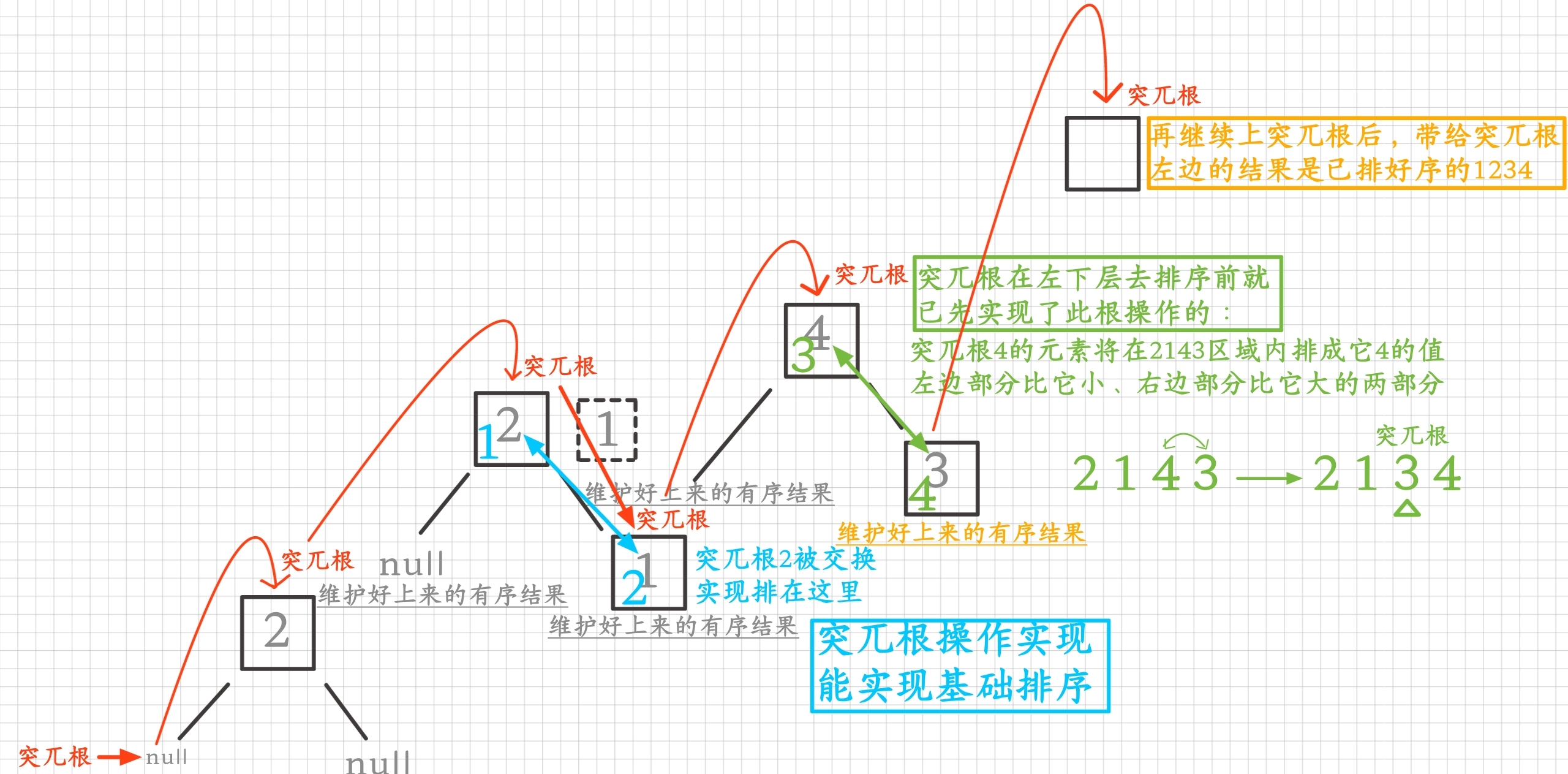
3.1設計過掉不符情況(在最底層時)
- if(array == null) return, 沒有元素不用排,下面是有元素
- if(strat ==?end) return,只有一個元素不用排,下面是多個元素
- if(strat > end) return,排不了不要排的,之后下面是符合正常情況的多個元素?
3.2查驗能實現基礎結果(在最底層往上點時)
當突兀根來到倒數第二層,當共有兩個元素下突兀根去作為在上層的會去操作實現上層與下兩層結果的表示連接時,左邊、右邊都是有序的結果,要實現它這層的有序結果要突兀根去操作實現為它的值比左邊的都大、比右邊的都小,操作具體實現為與1節點的值進行交換完成突兀根的實現操作,實現了突兀根所在的上層結果與下層左右兩斷開結果的連接表示,說明突兀根的實現操作在底層確實是能完成基礎排序的
3.3跳轉結果繼續往上回搭
4.實質
用二叉樹遞歸實現排序實質上還是確定元素大小排在的數組位置遞歸完一個個來排的:
它排的位置左邊都比它小、右邊都比它大,它排的位置就是它在數組中排的大小位置,同時也確定著其它元素的相對大小排位位置,所以最后一層元素不去找基準排位置也是相對已確定下來的不用去排,所以if(start == end)return的
二、快速排序的基準排序
待排序元素將其所在的待排序區域調整劃分成以它為基準值左邊都比它小、右邊都比它大的兩部分,并將它基準值放入兩部分的中間就完成了此元素的排序
1.雙路雙向交換鋪(Hoare法)
1.1原理
要去排的元素基準值在待排序區域里面任意取好后,在待排序區域左右兩端往內相遇鋪路,右端往內鋪遇小不符等停,左端往內鋪遇大換過去交換,直至路頭遇相等,此時路頭位置即基準元素大小排在的位置,最后將基準元素交換過去就完成了此元素的排序

1.2實現
private static int partition(int[] array, int left, int right) {int i = left;int j = right;int pivot = array[left];while (i < j) {while (i < j && array[j] >= pivot) {j--;}while (i < j && array[i] <= pivot) {i++;}swap(array, i, j);}swap(array, i, left);return i;}1.2.1>=
遇到與基準值相等大小的元素時直接作為可行的路過掉的因為與基準值相等大小的元素到最后排序在此作為基準元素左右兩邊都是可以的,所以此時排放在基準的左右兩路最后成兩部分都是可以的
1.2.2先右再左
基準為路的相遇點,要設置在屬于左路因為最后基準交換放到相遇點,基準值放到相遇點進去排序,相遇點的值會交換放到第一個位置即基準值的左邊需要是左路的部分,所以每輪的鋪路都是先進行右路的鋪完到左邊停再進行左路的鋪
2.雙路雙向覆蓋鋪(挖坑法)
2.1原理
要去排的元素基準值在待排序區域內任意取好并挖成坑,從左右端先左或右都行往同向內互相埋坑時又挖坑地推坑,推坑時始終是一端路停在坑位等著另一端路往內鋪路挖到坑填上,所以左右路兩端相遇時一定遇在坑位,此位置就是基準元素大小排序的位置排好
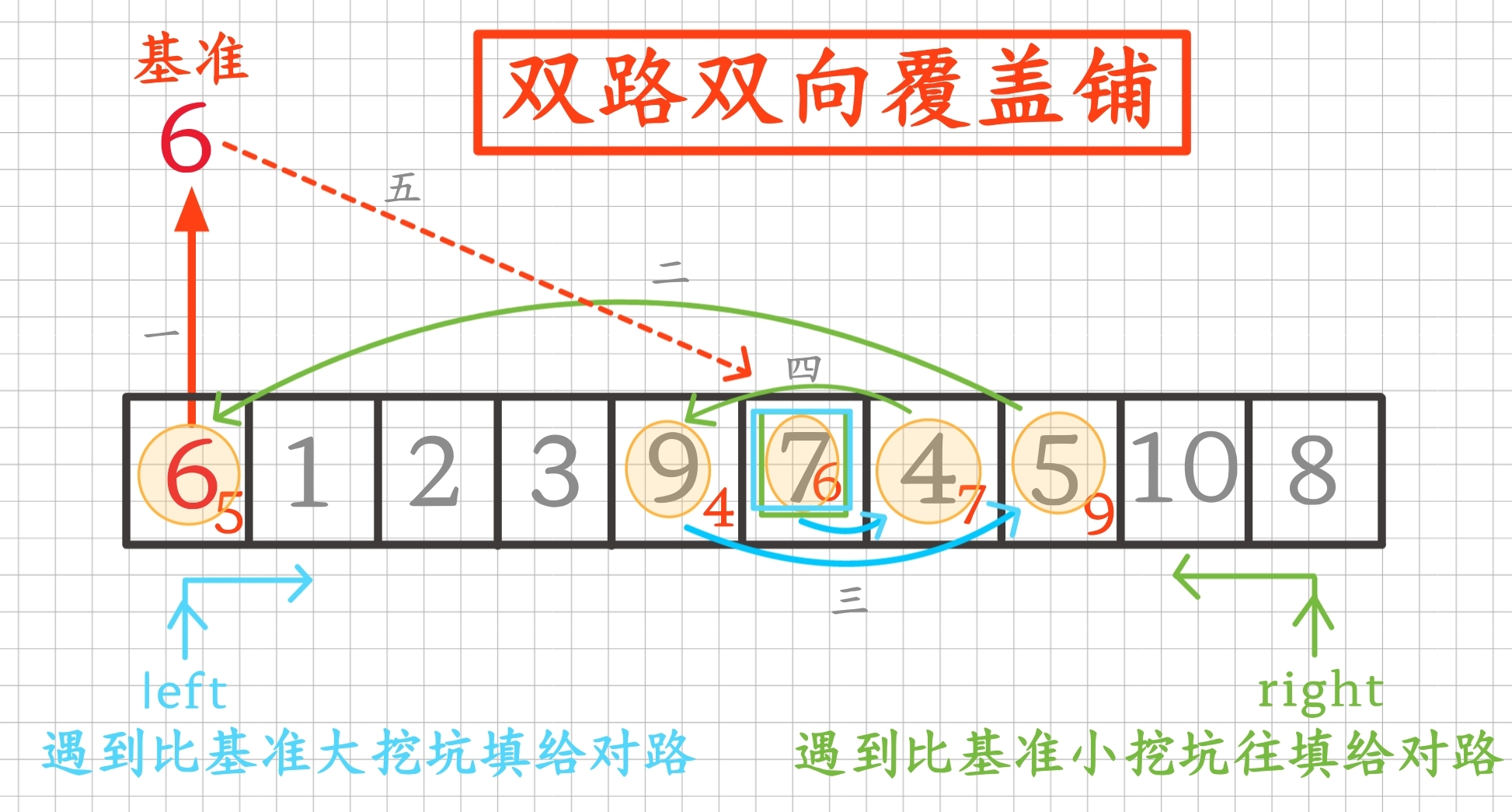
2.2實現
private static int partition(int[] array, int left, int right) {int i = left;int j = right;int pivot = array[left];while (i < j) {while (i < j && array[j] >= pivot) {j--;}array[i] = array[j];while (i < j && array[i] <= pivot) {i++;}array[j] = array[i];}array[i] = pivot;return i;}3.雙路單向交換鋪(前后指針法)
3.1原理
要去排序的基準元素在待排序區間任意選好后,定義prev與cur兩前后指針,在排序區間的一端開始同向往另一端通過前后交換動態維護prev及之前的區間為小路、cur及到prev之前的區間為大路,這樣當cur遍歷完排序區間時,數組就被分好了小路與大路兩部分,再將基準元素交換放到prev指針位置處,一個基準元素就在待排序區間排好了
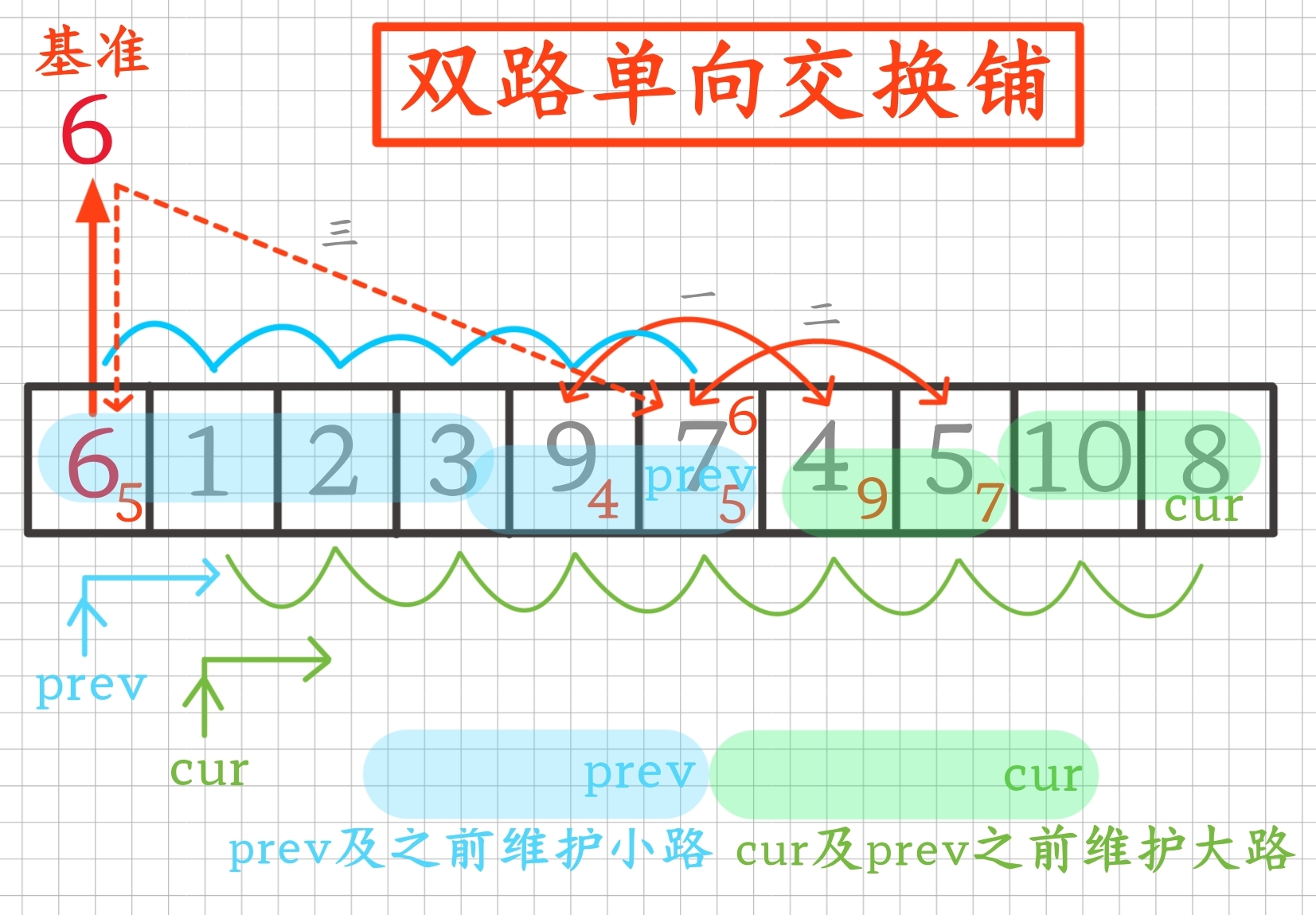
3.2實現
private static int partition(int[] array, int left, int right) {int prev = left ;int cur = left+1;while (cur <= right) {if(array[cur] < array[left] && array[++prev] != array[cur]) {swap(array,cur,prev);}cur++;}swap(array,prev,left);return prev;}三、快速排序的復雜度
基準排序的特點
- 元素的直接位置排好也排好著其它元素的間接位置排好、減少著其它元素剩下的需要排的量
- 每一個節點的出現,就是其完成它所在待排區域的基準排位標志?
1.時間復雜度
遞歸的調用語句算的是調用里面執行的內容(調用本身不算),每次調用里面的常量次數執行語句不算(因為乘常量常量可忽略的),只算里面的找調基準排的非常量級的時間復雜度,算時間復雜度時就一層層地算每層里面所有遞歸調用的時間和:
1.1完全順序逆序
1.1.1結構影響
當元素完全順序或完全逆序排時,其呈現的二叉樹結構為單分支的二叉樹:
- 一層層下來每層里面只劃分出了一個的遞歸調用,它這樣排能間接排出不用去排的元素只有一個(即只有一個葉子節點的元素)
1.1.2時間
最開始第一層時間是n-1,再下層一個元素已經排好了時間是n-2,到最后一層時最后一個元素被間接排好遞歸調用函數里面是直接return的,所以一共有n層,n-1層要去算時間,從上往下每層的時間從n-1減到1的等差數列和,最后大O算成的時間復雜度為O(n^2),實際上的時間會比n^2少
1.2完全二叉樹序
1.2.1結構影響
當數組呈完全二叉樹排列時:
- 每個節點排時都有間接最大地去排著其它元素的位置,一層層下來在每層里剩下區域會越來越多地被劃分著去排的,在一層中將會去完成更多的在區間中的排序,到最后一層能間接排出不用去排的元素會有很多
- 一個區間里,元素去基準排劃分的次數固定是元素個數少1的,劃分成更多的區間里去排,排序本身就會減這么區間多個的次數完成
1.2.2時間
因為每一層往下已排好的元素越來越多,每一層中所有基準區間總的去排的次數會越來越少,到最后一層里會有許多通過間接排就排好的元素不需要去排的,但大O算時的最后結果是偏大地算為每層所有找基準排的時間為固定的n,然后樹的高度為log(n),時間復雜度為O(n*log(n)),實際上的時間會比它少很多(根節點高度視為0的)
2.空間復雜度
因為遞歸調用的棧空間是動態復用的,所以空間復雜度為遞歸樹的最大高度下算每層開辟的空間,因為這里每層遞歸函數里面開辟的空間是常量級的,所以大O算排序遞歸的空間復雜度就為遞歸調用棧的深度即二叉樹的高度:
- 當數組完全順序或逆序時,二叉樹的高度為n-1,空間復雜度為O(n)
- 當數組呈完全二叉樹排列時,二叉樹的高度為log(n),空間復雜度為O(log(n))
3.優化
二叉樹每層分支得越多裝得越滿:
- 每個元素節點都會去間接排其它元素的兩部分位置、更多的在區間的排序減的次數會更多、以層單位去算時間的層的量會更少、從上往下已排出剩下的待排序元素會越來越少很多、最后通過間接排出位置不用去排的元素就會更多,時間復雜度會更低
- 二叉樹的高度更小下,空間復雜度也會更低
3.1三數取中
在每個待排序區間雖然是可以任意取元素作基準,但我們盡量取大小排在中間的元素使生成的樹分支更多樹更矮時間復雜度與空間復雜度都更低,我們采用三數取中法,即得到待排序區間后,在區間的首中尾的三個數比較下拿更小值更有可能得使得取的基準值大小更偏中一點
3.2插入排序
3.2.1棧溢出原因
當二叉樹經上層已排好序節點能確定往下再分更多的更小的待排序區間去排序時,在二叉樹下幾層會分出很多的待排序子區間去排序,除了最底層的不需要去排序,其它在上層的每個區間的一次排序函數里都會執行到再調用下層的兩個遞歸,在此時由于待排序子區間被分的特別多,會連續調用特別多的函數,一時間開辟特別多的函數棧幀,很有可能會造成棧溢出
3.2.2利與弊
因此在最后幾層的許多待排序子區間去排序時,我們可以直接在倒數的上幾層中就開始截斷,不再往下通過分更多的子區間去基準排序了,直接在這一層將待排序區域用插入排序直接排好,因為經過上層的有很多元素已經排好了位置,剩下的待排序元素也是間接地比較有序的,用插入排序也可以高效地完成,就不用去開辟下層大量聚集的函數棧幀避免了棧溢出,降低了開辟空間的成本
但是由于快速排序原本最后一層的元素通過上層元素的排好序全部可以間接地不用去排直接排好的,改成了插入排序后時間復雜度可能會比原來的純快速排序更高了
下載安裝教程 - 兼容老舊Windows系統)


)

)




)
:ListView基本使用)




)


