1 為什么需要四叉樹？

路徑規劃的本質是在給定環境中尋找從起點到終點的最優或可行路徑，其核心挑戰在于如何高效處理環境信息。傳統柵格法將環境均勻劃分為等大小的網格，雖直觀但面臨“維度災難”——環境規模擴大時，計算量呈指數級增長。例如，一個100×100的二維柵格地圖需維護10000個節點，而三維環境下這一數字將飆升至百萬級別。拓撲圖路徑規劃算法的核心思想在于將復雜的高維連續空間抽象為低維的離散圖結構。基于障礙邊界的可視圖法(運動規劃實戰案例 | 基于可視圖的路徑規劃算法(附ROS C++/Python仿真))以及維諾圖法(路徑規劃 | 詳解維諾圖Voronoi算法(附ROS C++/Python/Matlab仿真))都屬于這類基于拓撲圖的路徑規劃。

本文介紹的四叉樹(Quadtree)這一數據結構，源于計算機圖形學中對二維空間的層次化分割思想：通過遞歸地將空間劃分為四個象限（即“四叉”），僅在需要時對特定區域進行細化，從而實現對空間信息的自適應管理。例如，在開闊區域使用粗粒度劃分以節省內存，在障礙物密集區域則進行多級細分以提升路徑精度。這種按需分配的特性，使得四叉樹在面對非均勻分布的環境時，能夠顯著降低數據存儲與處理的冗余度

接下來，將詳細介紹基于四叉樹路徑規劃的算法原理

2 基于四叉樹的路徑規劃

基于四叉樹的路徑規劃(Quartree-based Path Planning)分為三個核心模塊：分層抽象、路圖搜索與動態剪枝

2.1 分層抽象

四叉樹的構建始于將整個環境空間視為一個根節點，隨后遞歸執行分割-判斷過程：若當前節點對應的區域完全自由或完全被障礙物占據，則停止分割；若區域同時包含自由空間與障礙物，則將其均等分為四個子節點。這一過程持續至達到預設分割深度或滿足精度要求，最終形成一棵層次化的樹結構。例如，在機器人導航場景中，四叉樹會在走廊等簡單區域保持頂層粗劃分，而在辦公室桌椅排列的復雜區域自動生成多層細粒度節點。這種分層抽象的特性，為路徑規劃算法提供了天然的優化通道，因為四叉樹可通過節點狀態快速排除無效區域：若某個父節點被標記為完全障礙，其所有子節點無需進一步探查；若父節點完全自由，則可直接將其作為整體加入開放列表。這種“剪枝”機制大幅減少了狀態擴展次數。

2.2 路圖搜索

首先，四叉樹路圖利用已有的樹節點作為路圖頂點。具體而言，選擇滿足以下條件的四叉樹節點作為路圖節點：

• 葉子節點中的自由節點，保證路徑可達性
• 非葉子節點中的自由父節點，用于跨層路徑跳躍

兩個四叉樹節點被判定為相鄰需滿足幾何邊界接觸條件：

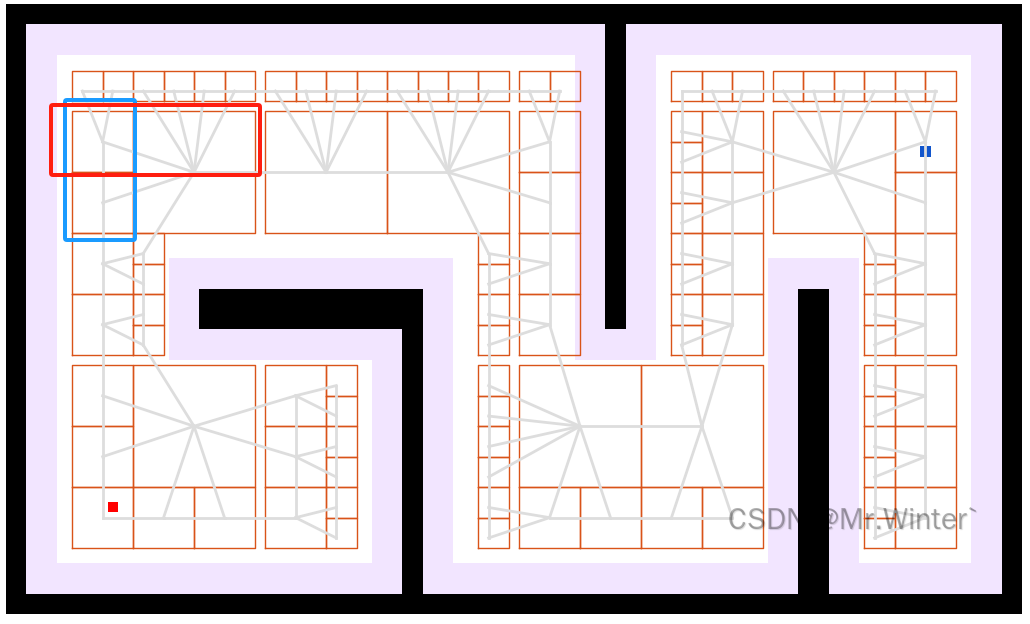
• 水平相鄰節點需滿足縱向坐標范圍存在重疊且橫向邊界間距在容差內(下圖紅框)
• 垂直相鄰節點需滿足橫向坐標范圍存在重疊且縱向邊界間距在容差內(下圖藍框)

每個四叉樹節點的中心點作為路徑搜索的潛在航路點，相鄰節點間建立帶權無向邊，邊的權重通常取兩節點中心點的歐氏距離。最終形成的路圖本質上是一個由自由空間節點及其連接關系構成的圖結構，其中節點密度在障礙物邊界區域顯著增加，確保路徑能夠精確繞行復雜障礙。

路徑搜索過程依托構建完成的路圖展開，采用Dijkstra算法即可。

2.3 動態剪枝

當環境中出現臨時障礙物（如突然出現的行人或車輛）時，傳統方法往往需要全局重新規劃，而四叉樹只需更新受影響區域的局部節點。具體而言，系統僅需回溯至包含障礙物變化的父節點層級，重新評估其子節點狀態，并選擇性觸發局部重構。這種增量式更新策略使得路徑規劃系統能夠以非常低的代價響應環境變化

3 算法仿真

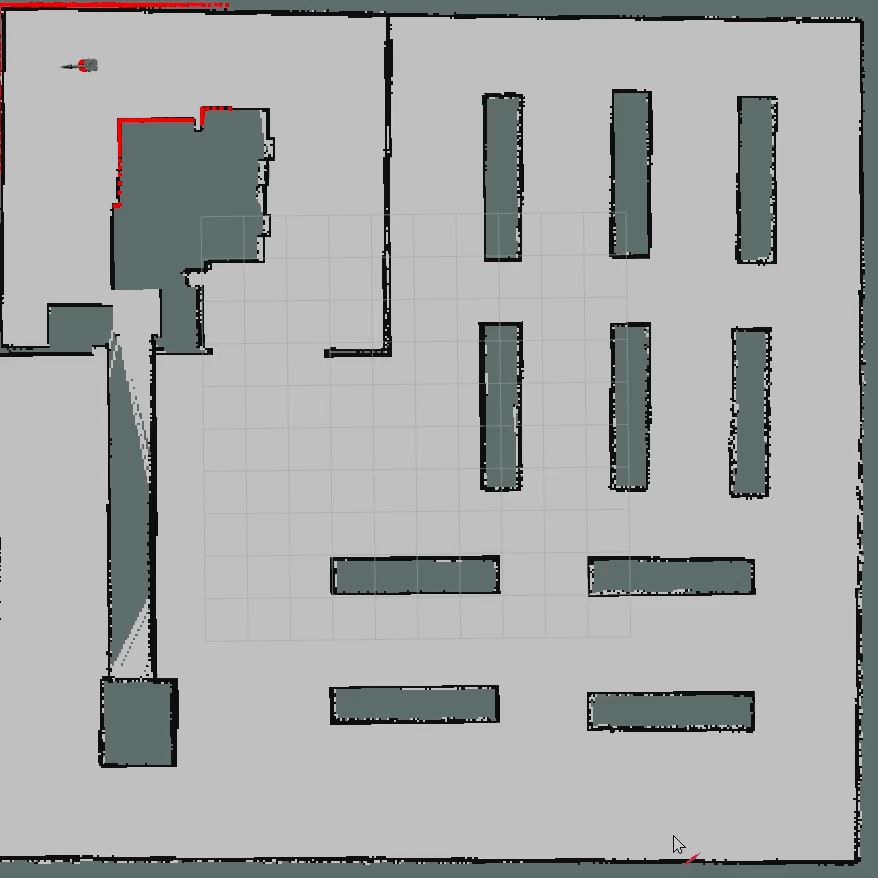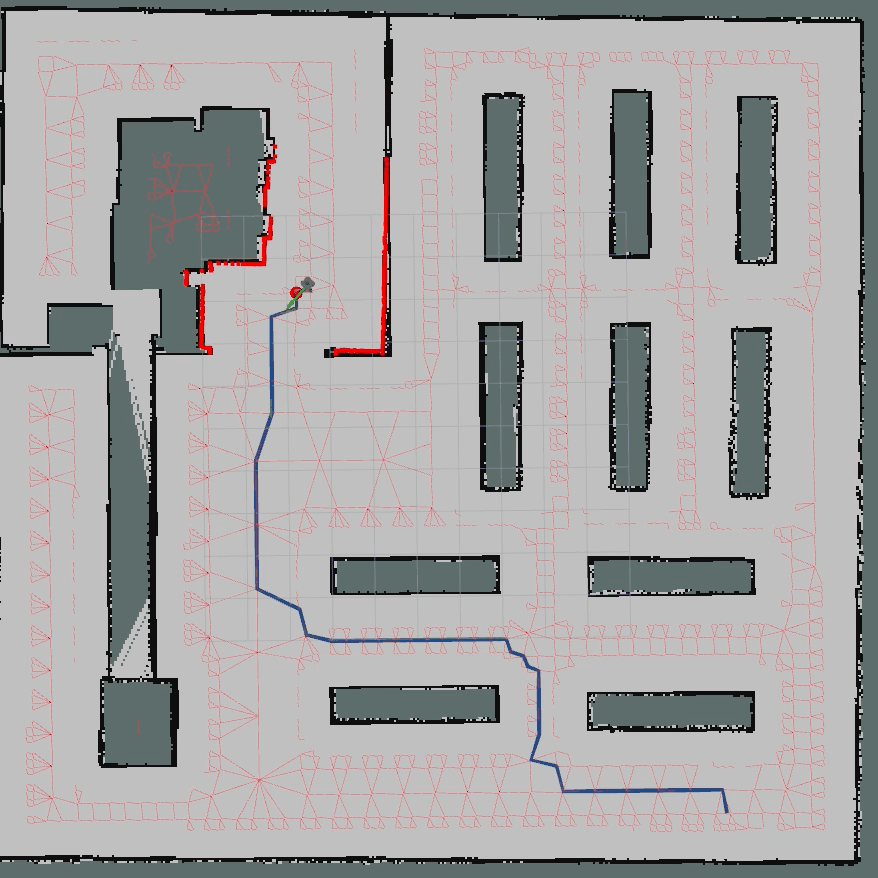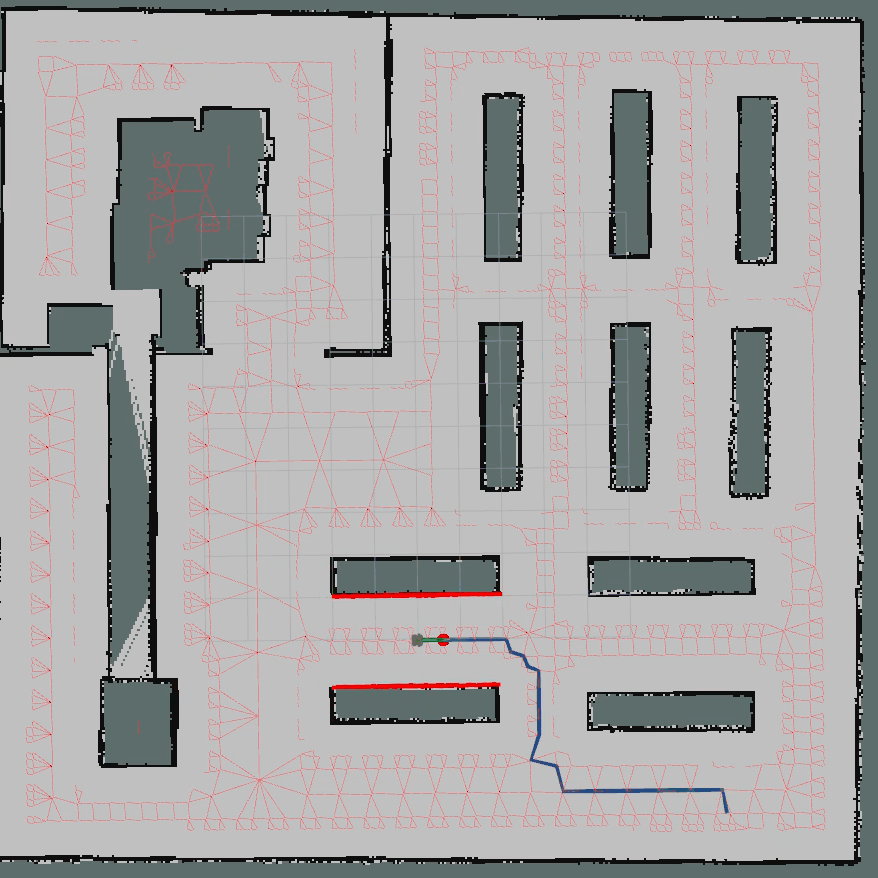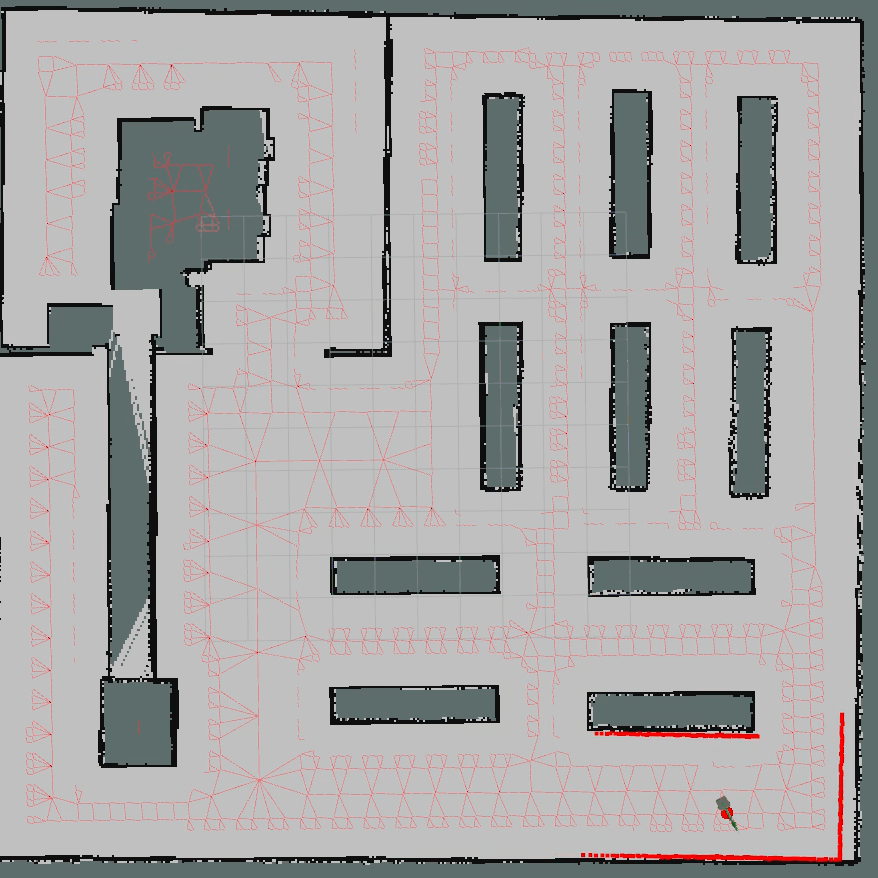
3.1 ROS C++算法仿真

核心代碼如下所示

bool QuartreePathPlanner::plan(const Point3d& start, const Point3d& goal, Points3d& path, Points3d& expand)
{double m_start_x, m_start_y, m_goal_x, m_goal_y;if ((!validityCheck(start.x(), start.y(), m_start_x, m_start_y)) ||(!validityCheck(goal.x(), goal.y(), m_goal_x, m_goal_y))){return false;}// construct quartree only onceif (!is_quartree_valid_){const size_t grids_num = quar_grids_.size();roadmap_.resize(grids_num);valid_edges_.reserve(grids_num * 4);for (size_t i = 0; i < grids_num; ++i){const auto& current = quar_grids_[i];for (size_t j = i + 1; j < grids_num; ++j){const auto& neighbor = quar_grids_[j];if ((std::abs(current.min_x() - neighbor.max_x()) <= 1.0 ||std::abs(current.max_x() - neighbor.min_x()) <= 1.0)){if (current.min_y() < neighbor.max_y() && current.max_y() > neighbor.min_y()){valid_edges_.emplace_back(current.center(), neighbor.center());const double dist = (current.center() - neighbor.center()).length();roadmap_[i].emplace_back(j, dist);roadmap_[j].emplace_back(i, dist);}}else if ((std::abs(current.min_y() - neighbor.max_y()) <= 1.0 ||std::abs(current.max_y() - neighbor.min_y()) <= 1.0)){if (current.min_x() < neighbor.max_x() && current.max_x() > neighbor.min_x()){valid_edges_.emplace_back(current.center(), neighbor.center());const double dist = (current.center() - neighbor.center()).length();roadmap_[i].emplace_back(j, dist);roadmap_[j].emplace_back(i, dist);}}}}is_quartree_valid_ = true;}...// search on quartree mapstd::vector<int> q_path;if (_searchOnRoadMap(roadmap_, start_idx, goal_idx, q_path)){path.clear();path.emplace_back(start);if (q_path.size() > 2){for (size_t i = 1; i < q_path.size() - 1; ++i){const auto& pt = vertices_[q_path[i]];// convert to world framedouble wx, wy;costmap_->mapToWorld(pt.x(), pt.y(), wx, wy);path.emplace_back(wx, wy);}}path.emplace_back(goal);return true;}else{return false;}
}

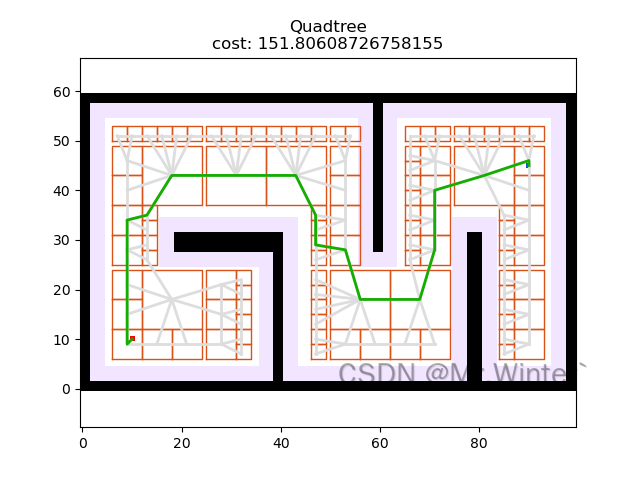
3.2 Python算法仿真

核心代碼如下所示

def partition(self, grid: np.ndarray, x: int, y: int, size: int, square_size_threshold: int = 5) -> List[Square]:"""Recursively divides the grid into four parts. If a part contains obstacles it further divied into four more parts.Parameters:grid (np.ndarray): 2D array representing the grid.x, y (int): Top-left coordinates of the current partition.size (int): Size of the current partition.Returns:List of Square objects representing free spaces in the grid."""if size < square_size_threshold:bottom_left = Point3d(x, y)top_right = Point3d(x + size, y + size)if self.isFree(grid, bottom_left, top_right):return [Square(bottom_left, top_right)]else:return []else:# Check if the area is homogeneous and free spaceif self.isFree(grid, Point3d(x, y), Point3d(x + size, y + size)):return [Square(Point3d(x, y), Point3d(x + size, y + size))]else:# Divide the area into quadrants and partition recursivelynew_size = size // 2quad1 = self.partition(grid, x, y, new_size)quad2 = self.partition(grid, x, y + new_size, new_size)quad3 = self.partition(grid, x + new_size, y, new_size)quad4 = self.partition(grid, x + new_size, y + new_size, new_size)return quad1 + quad2 + quad3 + quad4

完整工程代碼請聯系下方博主名片獲取

---

🔥 更多精彩專欄：

• 《ROS從入門到精通》
• 《Pytorch深度學習實戰》
• 《機器學習強基計劃》
• 《運動規劃實戰精講》
• …

👇源碼獲取 · 技術交流 · 抱團學習 · 咨詢分享 請聯系👇