論文地址：Matrix Information Theory for Self-Supervised Learning
代碼地址：https://github.com/yifanzhang-pro/matrix-ssl
bib引用：

@article{zhang2023matrix,title={Matrix Information Theory for Self-Supervised Learning},author={Zhang, Yifan and Tan, Zhiquan and Yang, Jingqin and Weiran, Huang and Yuan, Yang},journal={arXiv preprint arXiv:2305.17326},year={2023}
}

InShort

提出Matrix - SSL方法，結合矩陣信息理論統一視角，改進自監督學習，在圖像和語言任務中表現優異，探討了有效秩與維度坍縮等相關理論。

1. 研究背景
   • 對比學習與非對比學習：對比學習通過對齊相似對象、分離不相似對象學習表示；非對比學習如SimSiam、Barlow Twins等不使用負樣本，最大熵編碼框架為部分非對比學習方法提供統一視角。
   • 理論研究現狀：對比學習的理論探索聚焦于對比損失的分解和理解；非對比學習的理論研究揭示了其與其他方法的聯系。
2. 方法
   • 矩陣信息理論基礎：定義矩陣熵、矩陣KL散度和矩陣交叉熵等概念，用于衡量矩陣間差異，為后續損失函數設計提供理論依據。
   • Matrix - SSL算法：提出Matrix - SSL，結合矩陣均勻性損失和矩陣對齊損失。前者使特征矩陣的交叉協方差矩陣與單位矩陣對齊，后者直接對齊自協方差矩陣，提升表示學習效果。
   • 與其他損失的關系：證明最大熵編碼（MEC）損失與矩陣均勻性損失的等價性（在常數項和因子范圍內），建立有效秩與矩陣KL散度的閉式關系。
3. 實驗
   • 實驗設置：在ImageNet數據集上進行自監督學習實驗，采用ResNet50作為骨干網絡，設置特定的數據增強、優化器和超參數。
   • 評估結果：在線性評估、遷移學習和半監督學習任務中，Matrix - SSL均優于SimCLR、BYOL等基線方法。在ImageNet線性評估中，100輪預訓練的Matrix - SSL比SimCLR的Top - 1準確率高4.6%；在MS - COCO遷移學習任務中，400輪預訓練的Matrix - SSL比MoCo v2和BYOL性能提升3%以上。
   • 消融實驗：研究對齊損失比例和矩陣對數實現的泰勒展開階數對性能影響，確定(\gamma = 1)和泰勒展開階數為4時效果最佳。
4. 語言模型應用：提出用矩陣交叉熵損失微調大語言模型，在數學推理數據集GSM8K上，相比標準交叉熵損失，使用Matrix - LLM損失微調的Llemma - 7B模型準確率提升3.1%。
5. 結論：提供矩陣信息理論視角理解和改進自監督學習，為未來算法設計提供思路，有望推動機器學習領域發展。

---

摘要

最大熵編碼框架為 SimSiam、Barlow Twins 和 MEC 等許多非對比學習方法提供了統一的視角。受該框架的啟發，我們引入了 Matrix-SSL，這是一種利用矩陣信息理論將最大熵編碼損失解釋為矩陣均勻性損失的新方法。此外，Matrix-SSL 通過無縫整合矩陣對齊損失，直接對齊不同分支中的協方差矩陣，增強了最大熵編碼方法。實驗結果表明，在線性評估設置下，MatrixSSL 在 ImageNet 數據集上優于最先進的方法，在遷移學習任務中，MatrixSSL 在 MS-COCO 上的性能優于最先進的方法。具體來說，在 MS-COCO 上執行遷移學習任務時，我們的方法僅用 400 個 epoch 就比以前的 SOTA 方法（如 MoCo v2 和 BYOL）高出 3.3%，而預訓練則需要 800 個 epoch。我們還嘗試通過使用矩陣交叉熵損失微調 7B 模型，將表示學習引入語言建模機制，在 GSM8K 數據集上比標準交叉熵損失高出 3.1%。

Introduction

對比學習方法（Chen 等人，2020a；He 等人，2020）專注于使相似的對象緊密對齊，同時拉開不相似對象的距離。這種基于直觀原則的方法帶來了深刻而有趣的見解。例如，SimCLR 已被證明在相似性圖上執行譜聚類（spectral clustering）（Tan 等人，2023b；HaoChen 等人，2021），并且 Wang 和 Isola（2020）強調了對比損失的兩個關鍵方面：對齊和均勻性。

對齊損失可確保相似對象緊密映射，而均勻性損失則促進了均勻分布的輸出特征空間，從而保留了最大信息。值得注意的是，許多現有的對比方法（Wu et al.， 2018;He et al.， 2020;Logeswaran & Lee， 2018;Tian et al.， 2020a;Hjelm等人，2018 年;Bachman et al.， 2019;Chen et al.， 2020a） 可以被視為這兩種損失類型的具體實現，這一觀點簡化了對它們核心機制的理解。

同時，人們對不使用負樣本的非對比學習方法越來越感興趣，例如 BYOL（Grill 等人，2020 年）、SimSiam（Chen 和 He，2021 年）、Barlow Twins（Zbontar 等人，2021 年）、VICReg（Bardes 等人，2021 年）等。其中，Liu 等人（2022 年）提出了一個有趣的理論框架，稱為最大熵編碼，提議在從相同輸入的不同增強中計算出的兩個特征矩陣$z_1$、$z_2$之間最大化以下損失：
${\mathcal{L}}_{MEC}=?\mu logdet\left(I_d+\lambda Z_1{Z}_2^{?}\right).$

雖然乍一看可能并不明顯，但上述損失函數鼓勵對特征嵌入進行最大熵編碼，這與對比學習方法中的均勻性損失類似。事實證明，這種公式自然涵蓋了其他幾種非對比方法（如 SimSiam、Barlow Twins）的損失函數，并且由此產生的算法 MEC 在性能上超過了以前的方法（Liu 等人，2022 年）（在 BYOL 中使用的逐元素對齊損失，如(|z_1 - z_2|_2)，可以看作是這種 MEC 損失中的低階泰勒展開項）。然而，對比方法和非對比方法的比較揭示了一些差異：

Learning Method	Loss Function
Contrastive Learning Non-contrastive Learning	Uniformity + Alignment Uniformity

這一觀察自然促使我們提出一個更廣泛、更具探索性的問題。在本文中，我們肯定地回答了這個問題，提出了一種方法，這種方法不僅整合了對比學習和非對比學習范式的優勢，而且還增強了這些優勢。

The existing maximum entropy encoding framework, however, does not explicitly differentiate between feature matrices from different branches, hindering its integration with alignment loss.
然而，現有的最大熵編碼框架并沒有明確區分來自不同分支的特征矩陣，這阻礙了它與對齊損失的集成。
為了彌補這一差距，我們引入了矩陣信息理論。 By extending classical concepts like entropy, Kullback–Leibler (KL) divergence, and cross-entropy to matrix analogs，我們提供了對相關損失函數的更豐富表示。值得注意的是，我們發現像 SimSiam、BYOL、Barlow Twins 和 MEC 這樣的方法可以被重新解釋為利用基于矩陣交叉熵（MCE）的損失函數，這是以前未被探索的聯系（見定理 4.1）。

我們提出的算法 Matrix-SSL 將矩陣對齊損失納入非對比方法中，從而提高了經驗性能。這種雙重關注為表示學習提供了額外的信息和更豐富的信號。
Matrix-SSL 包括 Matrix-Uniformity（矩陣均勻性）和 Matrix-Alignment（矩陣對齊）損失組件。
Matrix-Uniformity 將特征矩陣$z_1$和$z_2$的互協方差矩陣與單位矩陣$I_d$對齊，而 Matrix-Alignment 則專注于對齊它們的自協方差矩陣（見圖 1）。作為副產品，我們觀察到有效秩和矩陣 KL 之間的封閉形式關系，這表明有效秩可以成為衡量各種機器學習方法性能的有力指標（見第 3.4 節）。

在實驗評估中，Matrix-SSL 在 ImageNet 數據集上的表現優于最先進的方法（如 SimCLR、BYOL、SimSiam、Barlow Twins、VICReg 等）。特別是在線性評估設置下，“我們的方法”僅用 100 個 epoch 的預訓練就能比 SimCLR 的 100 個 epoch 預訓練效果高出 4.6%。對于像 COCO 檢測和 COCO 實例分割這樣的遷移學習任務，“我們的方法”在僅用 400 個 epoch 的情況下比之前的最先進方法如 MoCo v2 和 BYOL 表現更好，效果高出最多達 3%，而這些對比方法需要 800 個 epoch 的預訓練。

我們進一步將表示學習引入語言建模領域，并使用矩陣交叉熵損失來微調大型語言模型，在 GSM8K 數據集上的數學推理任務中取得了最先進的結果，比標準交叉熵損失的效果高出 3.1%。

貢獻總結：
? 我們證明了非對比學習中 MEC 損失和矩陣均勻性損失（直至常數項和因子）的等效性，以及有效秩和矩陣 KL 之間的封閉式關系。
? 我們為對比和非對比學習方法提供了均勻性損失加對齊損失的統一視角。
? 我們在各種任務下實證驗證了我們的方法，包括圖像分類任務的線性評估、對象檢測和實例分割任務的遷移學習，以及數學推理任務的大型語言模型微調。

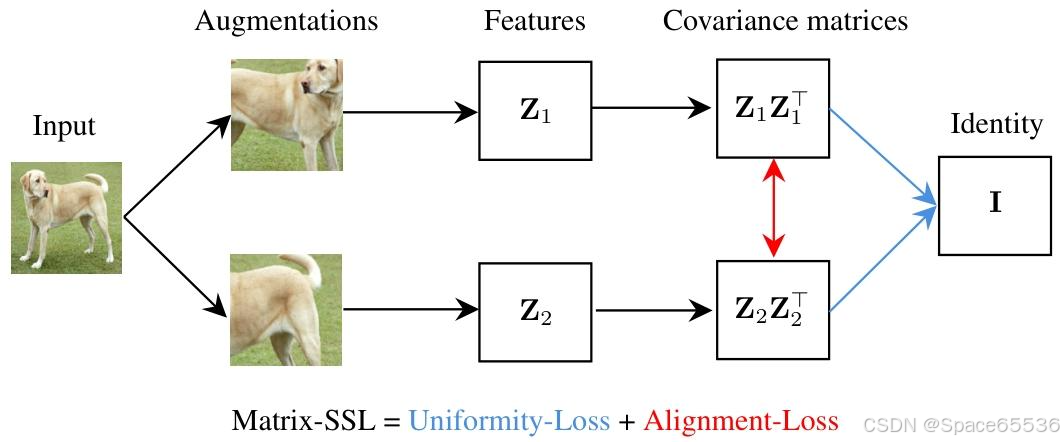
Figure 1. Illustration of the Matrix-SSL architecture. 首先是圖像輸入層，接著是數據增強和特征提取，然后形成協方差矩陣（$Z_1{Z}_1^{?}$和$Z_2{Z}_2^{?}$）。

9.結論

在本文中，我們提供了一個矩陣信息論視角，用于理解和改進自我監督學習方法。我們相信，我們的觀點不僅會提供對自我監督學習方法的精致和替代理解，而且還會成為未來設計越來越健壯和有效的算法的催化劑。

補充1：關于文中提到的KL散度

論文中提及KL散度（Kullback–Leibler Divergence），主要用于衡量兩個概率分布之間的差異，在矩陣信息理論的框架下，與自監督學習方法的設計、理解和優化相關。

1. 理論基礎：在論文提出的矩陣信息理論中，對經典信息論概念進行拓展，定義了矩陣KL散度。對于兩個正半定矩陣$P,Q\in {\mathbb{R}}^{n\times n}$，矩陣KL散度定義為$MKL(P\Vert Q)=tr(PlogP?PlogQ?P+Q)$。這一概念為對比不同矩陣提供了有力工具，是后續理論推導和損失函數設計的基礎。
2. 與損失函數關系：論文證明了總編碼率（TCR）損失與基于矩陣交叉熵（MCE）和矩陣KL散度的損失之間存在緊密聯系。定理4.1表明，在特定條件下，TCR損失可以轉化為正則化協方差矩陣與縮放單位矩陣之間的MCE/MKL損失。這種聯系揭示了不同損失函數之間的內在一致性，為理解和改進自監督學習方法提供了新視角。在實際應用中，通過調整相關參數，可利用這種聯系優化損失函數，提升模型性能。
3. 解釋學習過程：矩陣KL散度用于解釋自監督學習過程中的一些現象。有效秩與矩陣KL散度之間存在閉形式關系，命題6.1指出$erank(\frac{1}{B}Z{Z}^{?})=\frac{d}{exp(MKL(\frac{1}{B}Z{Z}^{?}\Vert \frac{1}{d}{I}_d))}$。在自監督學習訓練中，矩陣KL散度（或MCE）會逐漸減小，意味著特征協方差矩陣$\frac{1}{B}Z{Z}^{?}$會逐漸與$\frac{1}{d}{I}_d$對齊。這解釋了為什么在訓練過程中有效秩會增加，以及模型如何學習到更有效的數據表示，幫助理解自監督學習方法的收斂行為和性能提升機制。
4. 優化模型性能：在設計損失函數時，利用矩陣KL散度的最小化性質。例如，在矩陣對齊損失中，通過優化矩陣KL散度，使不同分支的協方差矩陣對齊，為模型提供更多信息和更豐富的信號，增強模型學習能力，從而提升在圖像分類、目標檢測、實例分割以及語言模型微調等任務中的性能。

補充2：關于論文提及的矩陣均勻性損失怎么促進特征有效分離和強化特征差異的

應用到跨模態圖文對比學習中的例子：特征提取與矩陣構建、損失函數設計、聯合訓練與優化

1. 特征提取與矩陣構建：對于輸入的圖像數據，利用如ResNet等卷積神經網絡進行特征提取，得到圖像特征向量，進而構建圖像特征矩陣；對于文本數據，使用Transformer等模型獲取文本特征表示，形成文本特征矩陣。假設輸入一張水果圖像和一段描述水果的文本，圖像經ResNet50提取特征后得到特征矩陣($Z_{1?image}$)，文本經BERT處理后得到特征矩陣($Z_{1?text}$) ，對其進行增強變換，獲得另一組特征矩陣($Z_{2?image}$)和($Z_{2?text}$)。
2. 損失函數設計：在圖像 - 文本對比學習中，結合矩陣均勻性損失和矩陣對齊損失進行優化。矩陣均勻性損失使圖像與文本的交叉協方差矩陣與單位矩陣對齊，公式為
   ${\mathcal{L}}_{Matrix?Uniformity}(Z_{image},Z_{text})=MCE(\frac{1}{d}{I}_d,C(Z_{image},Z_{text}))$，
   以此促進特征的均勻分布。矩陣對齊損失則關注圖像和文本自協方差矩陣的對齊，公式為${\mathcal{L}}_{Matrix?Alignment}(Z_{image},Z_{text})=?tr(C(Z_{image},Z_{text}))+\gamma ?MCE(C(Z_{image},Z_{image}),C(Z_{text},Z_{text}))$，
   通過調整(\gamma)控制對齊程度，強化特征之間的關聯。
3. 聯合訓練與優化：將圖像和文本數據同時輸入模型，以矩陣均勻性損失和矩陣對齊損失之和作為總損失
   (${\mathcal{L}}_{Matrix?SSL}={\mathcal{L}}_{Matrix?Uniformity}+{\mathcal{L}}_{Matrix?Alignment}$) ，采用隨機梯度下降等優化算法對模型進行訓練。在訓練過程中，不斷調整模型參數，使損失函數最小化，從而學習到更有效的圖像和文本特征表示，提升模型在跨模態任務中性能。

【關于非對比學習方法更關注特征的均勻分布】：
非對比學習方法通過設計特定的損失函數，使得模型學習到的特征在空間中盡可能均勻地分布，避免特征聚集在某些局部區域。這有助于模型捕捉到數據更全面的特征，提升其泛化能力。

• 原理：在非對比學習中，假設我們有一個圖像數據集，里面包含各種不同類別的圖像。以最大熵編碼（MEC）損失為例，公式為(${\mathcal{L}}_{MEC}=?\mu logdet\left(I_d+\frac{d}{B{?}^2}{Z}_1{Z}_2^{?}\right)$)，其中($Z_1$)和($Z_2$)是對同一輸入圖像進行不同增強變換后得到的特征矩陣。這個損失函數鼓勵特征嵌入的最大熵編碼，本質上就是讓特征在特征空間中分布得更均勻。從直觀上理解，當特征均勻分布時，每個特征維度都能攜帶獨特的信息，就像在一個二維平面上，如果所有點都聚集在一個小區域，那么很多區域的信息就被忽略了；而當這些點均勻分布時，整個平面的信息都能被充分利用。在實際的圖像特征學習中，均勻分布的特征可以更好地描述圖像的不同屬性，使得模型對不同圖像的區分能力更強。
• 示例：假設有一個包含貓、狗、汽車三類圖像的數據集。使用非對比學習方法訓練模型時，模型會嘗試讓貓的圖像特征、狗的圖像特征以及汽車的圖像特征在特征空間中均勻分布。比如，在一個三維的特征空間中，貓的特征點不會都集中在一個角落，而是會均勻地散布在空間的某個區域；狗和汽車的特征點也會各自均勻地分布在不同區域，并且這些區域之間有明顯的區分度。這樣，當遇到一張新的貓的圖像時，模型可以根據其特征在均勻分布的特征空間中的位置，更準確地判斷它屬于貓這一類。如果特征不是均勻分布，比如貓和狗的特征點有很多重疊，那么模型在區分這兩類圖像時就容易出錯。

【假如有些貓和有些狗有相似的特征呢？比如黑貓和黑狗，這種情況學習兩種辨別性特征的可行性】：
在存在相似特征的情況下，如黑貓和黑狗，該方法仍能有效學習兩種視覺對象的表征，主要通過以下幾個方面來實現：
矩陣均勻性損失促進特征分離：矩陣均勻性損失使得特征分布更加均勻，即便黑貓和黑狗存在相似特征，在均勻分布的特征空間中，它們也會被分配到不同的區域。以二維特征空間為例，假設一個維度代表顏色相關特征，另一個維度代表形狀相關特征。雖然黑貓和黑狗在顏色（黑色）上相似，但在形狀上有差異。均勻性損失會促使模型將黑貓和黑狗的特征在形狀維度上充分展開，避免因顏色相似而聚集在一起，從而使模型能夠區分兩者。
矩陣對齊損失強化特征差異：矩陣對齊損失通過對齊不同分支的協方差矩陣，進一步突出了黑貓和黑狗之間的特征差異。模型會學習到黑貓和黑狗各自獨特的特征組合模式。比如，黑貓可能具有獨特的面部斑紋和體型特征，黑狗雖然顏色相同，但面部和體型特征不同。矩陣對齊損失使得模型能夠捕捉到這些細微差異，在協方差矩陣層面強化這種區分，進而更好地區分黑貓和黑狗。
數據增強增加特征多樣性：在訓練過程中，通常會使用多種數據增強技術，如隨機裁剪、顏色抖動、高斯模糊等。對于黑貓和黑狗的圖像，數據增強會引入更多的差異。例如，對黑貓進行顏色抖動可能使其黑色呈現出不同的灰度變化，而對黑狗進行相同操作時，由于其毛發質地等差異，變化效果會有所不同。這些通過增強引入的差異有助于模型學習到更多區分兩者的特征，即使它們原本有相似的顏色特征，也能在多樣化的增強特征中找到區分點。
模型學習能力與特征挖掘：深度神經網絡本身具有強大的學習能力。面對黑貓和黑狗的相似特征，模型會自動挖掘其他更具區分性的特征。如黑貓和黑狗的眼睛形狀、耳朵形態等細節特征，模型在訓練過程中會逐漸關注到這些特征，并將其融入到特征表示中。結合矩陣信息理論的損失函數，模型能夠更有效地利用這些挖掘到的特征，從而準確地區分兩種視覺對象的表征。

【或者說：那擴展到圖像和文本的匹配關系：文本1：黑貓；文本2：黑狗；圖像1：黑貓的圖像；圖像2：黑貓的圖像，這種情況下應用Matrix-SSL的解釋】：特征提取、矩陣構建、損失函數計算

特征提取與矩陣構建：利用預訓練的圖像模型（如ResNet）和文本模型（如BERT）分別對圖像和文本進行特征提取。對圖像1和圖像2提取特征后得到圖像特征矩陣$Z_{image1}$、$Z_{image2}$，對文本1和文本2提取特征后得到文本特征矩陣$Z_{text1}$、$Z_{text2}$。這些特征矩陣包含了圖像和文本的語義信息，例如圖像特征矩陣可能編碼了黑貓的顏色、形狀、姿態等視覺特征，文本特征矩陣則包含了“黑貓”“黑狗”這些詞匯所蘊含的語義信息 。

矩陣均勻性損失的作用：計算圖像與文本之間的矩陣均勻性損失，如${\mathcal{L}}_{Matrix?Uniformity}(Z_{image1},Z_{text1})=MCE(\frac{1}{d}{I}_d,C(Z_{image1},Z_{text1}))$。這一損失促使圖像和文本的交叉協方差矩陣向單位矩陣對齊，使得特征分布更均勻。在這個例子中，對于“黑貓”的圖像和文本，均勻性損失會讓模型學習到兩者在特征表示上的一致性，同時避免特征過于集中在某些相似維度（如“黑色”這一特征維度）。即使黑貓和黑狗在顏色上有相似性，但均勻性損失會推動模型在其他維度（如形狀、品種特征等）挖掘差異，從而更準確地匹配“黑貓”的圖像和文本。

矩陣對齊損失的作用：矩陣對齊損失
${\mathcal{L}}_{Matrix?Alignment}(Z_{image1},Z_{text1})=?tr(C(Z_{image1},Z_{text1}))+\gamma ?MCE(C(Z_{image1},Z_{image1}),C(Z_{text1},Z_{text1}))$
用于直接對齊圖像和文本的自協方差矩陣。在“黑貓”的圖像和文本匹配中，它幫助模型強化圖像和文本特征之間的關聯。比如，圖像中黑貓獨特的外貌特征（如綠色的眼睛、黑色的毛發質感）與文本“黑貓”所蘊含的相關語義特征通過矩陣對齊損失得到更好的匹配。而對于“黑狗”的文本和“黑貓”的圖像，由于兩者自協方差矩陣差異較大，矩陣對齊損失會使得模型減少對它們的匹配度，從而正確區分不同的圖像 - 文本對。

整體匹配判斷：通過最小化矩陣均勻性損失和矩陣對齊損失的總和
（即${\mathcal{L}}_{Matrix?SSL}={\mathcal{L}}_{Matrix?Uniformity}+{\mathcal{L}}_{Matrix?Alignment}$），模型能夠學習到圖像和文本之間的準確匹配關系。在這個例子中，“黑貓”的圖像1與文本1之間的損失會在訓練過程中逐漸減小，表明模型認為它們是匹配的；而圖像1與文本2（“黑狗”）之間的損失會相對較大，模型能夠識別出這兩者不匹配。這樣，模型就可以在圖像和文本之間建立有效的匹配關系，即使存在相似特征的干擾，也能準確判斷圖像和文本是否對應 。

補充3：代碼

參考：https://github.com/yifanzhang-pro/Matrix-SSL/blob/master/main_pretrain.py
Matrix-SSL 損失函數由 Matrix-Uniformity Loss 和 Matrix-Alignment Loss 兩部分組成：
$L_{\text{Matrix-SSL}}=L_{\text{Matrix-Uniformity}}+L_{\text{Matrix-Alignment}}$
其中：

1. Matrix-Uniformity Loss 旨在使特征的協方差矩陣接近單位矩陣，以促進特征的均勻分布：
   $L_{\text{Matrix-Uniformity}}(Z_1,Z_2)=\text{MCE}\left(\frac{1}{d}{I}_d,C(Z_1,Z_2)\right)$
   其中 ( $C(Z_1,Z_2)=\frac{1}{B}{Z}_1{H}_B{Z}_2^{?}$ )，( $H_B$ ) 是用于中心化的矩陣。

2. Matrix-Alignment Loss 通過對協方差矩陣之間的差異進行對齊：
   $L_{\text{Matrix-Alignment}}(Z_1,Z_2)=?\text{tr}(C(Z_1,Z_2))+\gamma ?\text{MCE}(C(Z_1,Z_1),C(Z_2,Z_2))$
   其中 ($\gamma$) 是權重因子，用于調整對齊損失的貢獻。

最小化矩陣均勻性損失和矩陣對齊損失的總和：

mec_loss = (loss_func(p1, z2, lamda_inv) + loss_func(p2, z1, lamda_inv)) * 0.5 / args.m
mce_loss = (mce_loss_func(p2, z1, correlation=True, logE=False, lamda=args.mce_lambd, mu=args.mce_mu, order=args.mce_order, align_gamma=args.align_gamma)+ mce_loss_func(p1, z2, correlation=True, logE=False, lamda=args.mce_lambd, mu=args.mce_mu, order=args.mce_order, align_gamma=args.align_gamma)+ args.gamma * mce_loss_func(p2, z1, correlation=False, logE=False, lamda=args.mce_lambd, mu=args.mce_mu, order=args.mce_order, align_gamma=args.align_gamma)+ args.gamma * mce_loss_func(p1, z2, correlation=False, logE=False, lamda=args.mce_lambd, mu=args.mce_mu, order=args.mce_order, align_gamma=args.align_gamma)) * 0.5
# mec_loss = mec_loss + mce_loss * 1.
# scaled loss by lamda
# loss = -1 * mec_loss * lamda_inv
loss = mce_loss

具體來說：

1. 矩陣的均勻性損失：

mec_loss = (loss_func(p1, z2, lamda_inv) + loss_func(p2, z1, lamda_inv)) * 0.5 / args.mdef loss_func(p, z, lamda_inv, order=4):p = gather_from_all(p)z = gather_from_all(z)p = F.normalize(p)z = F.normalize(z)c = p @ z.Tc = c / lamda_inv power_matrix = csum_matrix = torch.zeros_like(power_matrix)for k in range(1, order+1):if k > 1:power_matrix = torch.matmul(power_matrix, c)if (k + 1) % 2 == 0:sum_matrix += power_matrix / kelse: sum_matrix -= power_matrix / ktrace = torch.trace(sum_matrix)return trace

2. 矩陣對齊損失：

mce_loss = (mce_loss_func(p2, z1, correlation=True, logE=False, lamda=args.mce_lambd, mu=args.mce_mu, order=args.mce_order, align_gamma=args.align_gamma)+ mce_loss_func(p1, z2, correlation=True, logE=False, lamda=args.mce_lambd, mu=args.mce_mu, order=args.mce_order, align_gamma=args.align_gamma)+ args.gamma * mce_loss_func(p2, z1, correlation=False, logE=False, lamda=args.mce_lambd, mu=args.mce_mu, order=args.mce_order, align_gamma=args.align_gamma)+ args.gamma * mce_loss_func(p1, z2, correlation=False, logE=False, lamda=args.mce_lambd, mu=args.mce_mu, order=args.mce_order, align_gamma=args.align_gamma)) * 0.5...
def mce_loss_func(p, z, lamda=1., mu=1., order=4, align_gamma=0.003, correlation=True, logE=False):p = gather_from_all(p)z = gather_from_all(z)p = F.normalize(p)z = F.normalize(z)m = z.shape[0]n = z.shape[1]# print(m, n)J_m = centering_matrix(m).detach().to(z.device)if correlation:P = lamda * torch.eye(n).to(z.device)Q = (1. / m) * (p.T @ J_m @ z) + mu * torch.eye(n).to(z.device)else:P = (1. / m) * (p.T @ J_m @ p) + mu * torch.eye(n).to(z.device)Q = (1. / m) * (z.T @ J_m @ z) + mu * torch.eye(n).to(z.device)return torch.trace(- P @ matrix_log(Q, order))

最后，總損失的計算：

total_loss = mec_loss + mce_loss
# 可以根據需要進行縮放等操作
# 例如：total_loss = -1 * total_loss * lamda_inv
loss = total_loss