1.二分搜索法

題目原文：

給定一個 n 個元素有序的（升序）整型數組 nums 和一個目標值 target ，寫一個函數搜索 nums 中的 target，如果目標值存在返回下標，否則返回 -1。

示例 1:

輸入: nums = [-1,0,3,5,9,12], target = 9
輸出: 4
解釋: 9 出現在 nums 中并且下標為 4

示例 2:

輸入: nums = [-1,0,3,5,9,12], target = 2
輸出: -1
解釋: 2 不存在 nums 中因此返回 -1

1.1什么是二分搜索法？

我們來看AI給出的回答：

二分搜索法，又稱折半查找算法，是一種在有序列表（如數組）中高效查找特定元素的搜索算法。該算法利用了列表元素已排序的特性，通過反復將待搜索區間分成兩半來縮小查找范圍，具體步驟如下：

1. 初始化: 確定搜索區間，通常開始時是整個列表，設兩個指針分別指向列表的起始位置（low）和結束位置（high）。

2. 計算中間位置: 計算當前搜索區間的中間索引 mid = (low + high) / 2，并獲取該位置的元素值。

3. 比較與決策:

   • 如果中間元素正好是要查找的目標，則搜索結束，返回該元素的位置。
   • 如果目標值小于中間元素，則在左半區間（low 到 mid-1）繼續搜索，更新 high = mid - 1。
   • 如果目標值大于中間元素，則在右半區間（mid+1 到 high）繼續搜索，更新 low = mid + 1。

4. 重復步驟2和3，直到找到目標值或搜索區間為空（即 low > high），此時表明目標值不在列表中。

二分搜索法的時間復雜度為 O(log n)，其中 n 是列表中元素的數量。這意味著對于大規模數據集合，二分搜索遠比順序搜索（時間復雜度為 O(n)）高效。然而，為了應用二分搜索，列表必須事先排序，且通常適用于靜態數據或不頻繁插入刪除操作的數據結構。

可以看出二分搜索法顧名思義就是不斷來縮小我們的搜索區間，來查找特定元素的一種高效算法，而在使用二分搜索法時，關鍵的地方就在于如何確定我們的區間邊界。

1.2解法思路

class Solution {
public:int search(vector<int>& nums, int target) {int left = 0;int right = nums.size()-1;while(left <= right){int madile = left+(right - left) / 2;if(nums[madile] > target){right = madile - 1;}if(nums[madile] < target){left = madile + 1;}if(nums[madile] == target){return madile;}}return -1;}
};

開始我們可以給定一個左閉右閉的區間，是左區間left = 0，右區間right = nums.size -1，此時判斷邊界時就需要考慮：左區間和右區間的關系時小于等于還是小于？

開始我們的思路時給定一個左閉右閉的區間，也就是說左區間的值可以等于右區間，所以在第一個邊界判斷時，我們的左區間是可以等于右區間的。

當我們對目標值進行判斷后，我們的左右區間又該如何判斷呢？

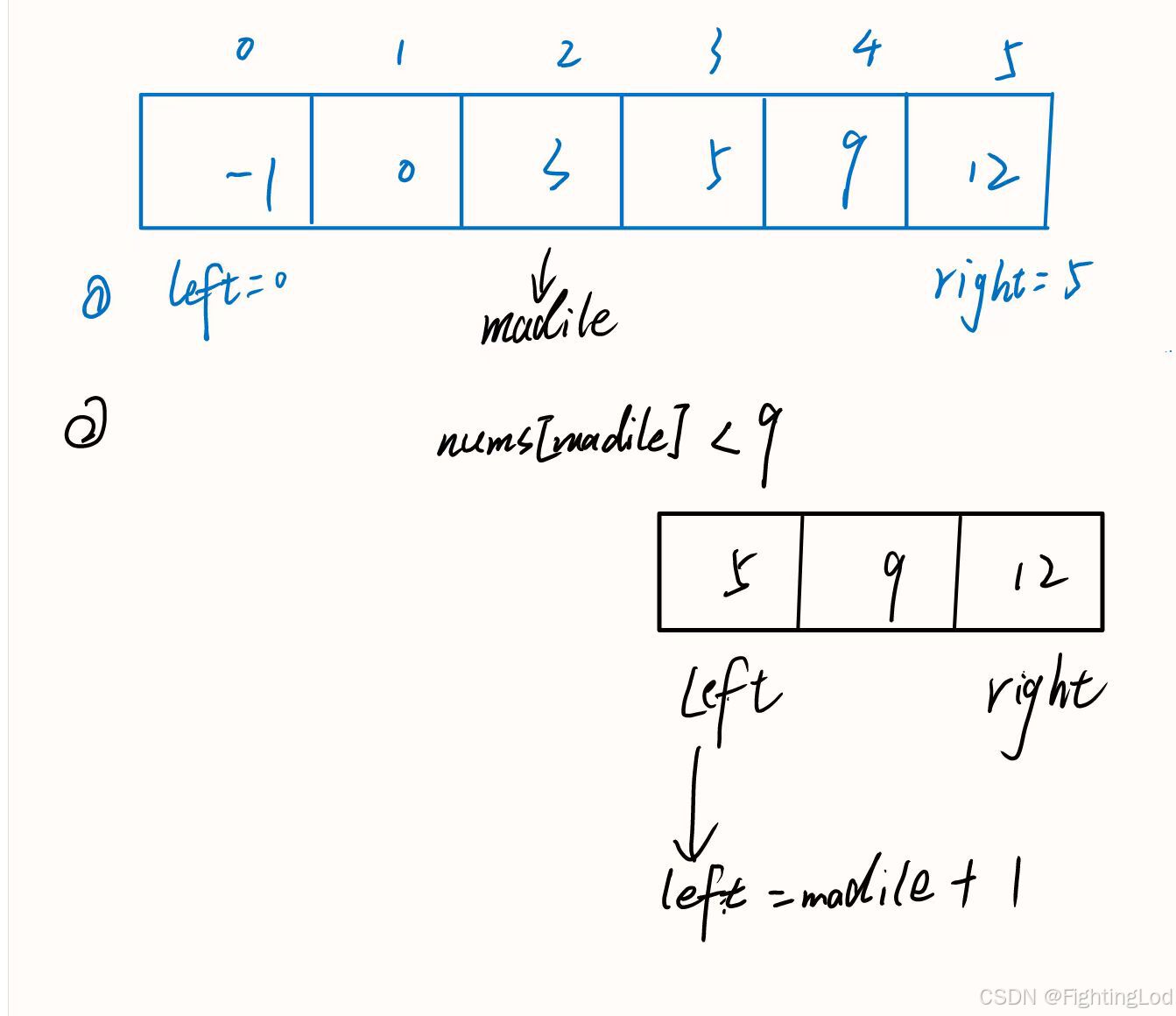
第一種情況：當我們所要查找的目標值小于區間中值時，我們需要考慮的是，此時的右區間right是等于madile還是等于madile-1，回到判斷條件中nums[madile] > target，這表示我們區間的中值已經大于我們的目標值了，所以我們下一次的判斷時，已經不需要考慮madile，所以此時的右區間應該是madile-1。

同樣的道理當區間中值小于目標值時，我們要更新左區間的值，此時左區間的值為madile+1。